Симметричные решения задачи синтеза трехзвенного ступенчатого СВЧ-фильтра Баттерворта

Ступенчатый СВЧ-фильтр представляет собой несколько регулярных отрезков линии передачи, последовательно включенных в волноводный тракт. Эти отрезки, являющиеся звеньями фильтра, имеют одинаковые электрические длины и различные волновые сопротивления. Такие фильтры предложены А. Л. Фельдштейном в 1959 году. Численный метод синтеза ступенчатых фильтров с произвольным количеством звеньев изложен в [1]. В настоящей работе получено аналитическое решение задачи синтеза трехзвенного ступенчатого СВЧ-фильтра с частотной характеристикой Баттерворта.

A = п A ⁽ j ’ , j = 1

где

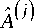
^ cos ( 9 )

7 sin ⁽⁹⁾

I z j

iz j sin ( 9 )^ cos ( 9 )

( j = 1,3 ) ,

i - мнимая единица, 9 - электрическая длина

звена, выражающаяся через постоянную распространения волны у:

9 = у l .

Соотношения (3) записаны при условии, что параметр у является действительной величиной и

1. Постановка задачи

принимает одинаковые значения для всех звеньев фильтра.

Подстановка (3) в (2) дает

На рис. 1 изображена эквивалентная схема трехзвенного ступенчатого фильтра, включенного в линию передачи с волновым сопротивлением z q . Волновые сопротивления звеньев фильтра обозначены через z j ( j = 1,з ) . Предполагается, что звенья имеют одинаковую длину l .

Комплексные амплитуды прямых волн напряжения на входе и выходе фильтра связаны соотношением [1]

1I . 1 ⁾

U 0 ( ° ⁾ = т| A 11 + A 12 ⁺ z 0 A 21 ⁺ A 22 I U 4 ^{( 3} l ) . ^{(1) 2}1 z 0 )

Здесь A mn ( m , n = 1,2 ) - элементы матрицы передачи фильтра A , которая определяется как произведение матриц передачи звеньев

A 11 = cos ( 9 )

cos ² ( 9 ) - — + — + — sin ² ( 9 ) I Zo Zo Zo I ' ' V 2    3    3 )

A 12 = i sin ( 9 )

A ₂₁

A 22 =^cos ( ⁹ )

Рис. 1

Fig. 1

( z 1 + z 2 + z 3 ) cos ² ( 9 )—1-3- sin ² ( 9 ) z ₂

1    1

--1-- z ₁ z ₂

—Los ² ( ⁹)— z ^-sm ² ( ⁹ ) , ^z 3 )             ^z 1 ^z 3          J

cos ² ( 9 ) -f z ² + z ³ ₊ z 3 ) sin ² ( 9 ) V ^z 1 ^z 1 ^z 2 )

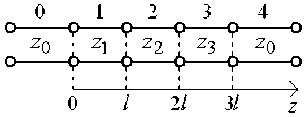
С учетом (4) формулу (1) можно записать в виде

#1 = 1 ( cos (0)

UI 4 ( 3 I ) 2        ^{( )}

2 cos ² ( 0 ) -

+ i sin ( 0 ) a ^{- 3} " f z⁰ , z ⁰

V ^z 1 ^z 2

, z 3 J

cos ² ( 0 ) -

- a1

:Ml z 0 z 2L I sin ² ( 0 )

V ^z1 z 3 J

Г ,

где введено обозначение

n

a n ^] ( X 1 , X 2 , ^ , X n ) = £

j = 1 ^V

xj ^{+ —} j x j J

I

■ ( n = V,- ) .

L

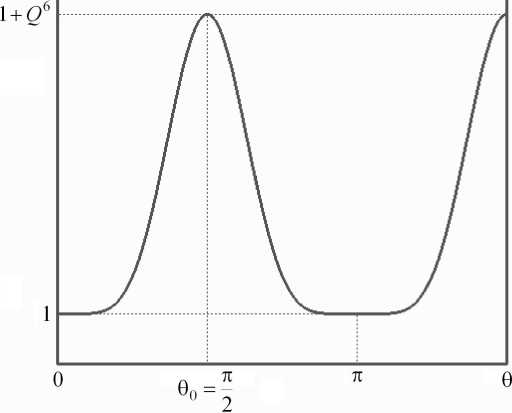
Рис. 2

Fig. 2

Рабочее затухание фильтра

L = | ^U 0 ( ⁰ ) / ^U 4 ( ^{3 l} )| ²

+ 4 a ^{[ 1 ]}

+ 2 a

можно представить в виде многочлена по степе-

ням sin ² ( 0 )

L = 1 + £ c j sin ^{2 j} ( 0 )

j = 1

z ₁ z ₃

Г „2^ z o z ²

V ^z 1 ^z 3

2_ I          _2_2 I z0z2     -1] z1z3

2 ^+a 2 2 ^z l ^z 3 ^J         I ^z 0 ^z2 ^J

Легко убедиться в том, что величины C_j удовлетворяют условиям

^{( j} =¹ ’ ^{3 )}

с коэффициентами

C 1

- 6 - 2 a ^{- 3 ]} l z 1 , z 1 , z 2 | +

V ^z 2 ^z 3 ^z 3 J

Sc j=1

= ¹ [ ^{a -1]}M ^- 2 _] .

Г _2 _r-3 ] 2 0 5

-2 „2 |

2., z 0 + 2d

₂ , ₂ , ₂

Г _2    _2    _2 I"

_r[ 3 ] J0_, j^, 2zi_

2 C , + C ₉ =

- 6 ₊ 2 a [ 1 ] | z 1 1 +

V ^z 3 J

zzz

V 1   2   3 J

z 1 z 2 z 1 z 3 z 2 z 3 J

,

г п Г 2    2    2'

_:^[3] z 1 z 1 z 2

„2’2’ ,2

V ^z 2

+ 2a^[

^z 3 ^z 3 J

[ ^МГ    Г³"

V ^z ₂ ^z 3 ^z 1 ^z ₂ J

-

C =¹

Г z z₉ |         [ 1 1 ! z |

6 + 4 a ^] l —,— 1 + 6 a ^] l — 1 +

V ^z 2 ^z 3 J         V ^z 3 J

- 2 a

+ a1

_r[ 3 ] f zX z\

. 2 I

2 , 2 , 2 z ₂ z ₃ z ₃

z ² - 2 ^

■   ( „2   2   2 1

. [ ³ ] ^z 0 ^z 0 ^z 0

¹        ,2 ’ 2 ’ 2

V ^z 1 ^z 2 ^z 3 J

. [ 1 ] JL

I ^z1^z . 3

- 2a^[

Г _2_   _2_ I"

z ₀ z ₂ z ₀ z ₂

V z ^; ,     ^j]

где

+ 2 a

Г 2

J1

V

^z 2 z 3 z i z 2

-z_ - 4 a

22 z ₀ z ₀

,

V ^z 1 z 2 z 2 z 3 J

z ² z ^{2 v} =aa .

z ₀ z ₂

- 6 a

_: И _00_

V z 1 z 3 J

- 2 a

Г 2 z e

V ^zi^z z 3

2 I" z ₀ z ₂

Ta J]

C ₃ =¹

- 2 - 2 a ' ² l z ¹ , z ²

V ^z 2 ^z 3

-

4 a ^{[ 1 ]} | z l V z 3.

-

- a

Г П Г 2    2    2 I

. ^[3 ] ^z 1 ^z 1 ^z 2

.2" 2, 2

V ^z 2 ^z 3 ^z 3 J

Г „2       „2

. ^[ 3 ] ^z 0 ^z 0 ^z 0 . 2’2, 2

V ^z 1 ^z 2 ^z 3

Рабочее затухание фильтра с частотной характеристикой Баттерворта задается соотношением

L = 1 + Q ⁶ sin ⁶ ( 0 ) .                                    (9)

График функции L ( 0 ) приведен на рис. 2. Обозначим через О 0 , у 0 и Л 0 значения электрической длины звена, постоянной распространения и длины волны в линии передачи, соответствующие первому максимуму рабочего затухания фильтра. Как следует из рис. 2, О 0 = п /2. Тем самым длина звена:

- 2 a

. . Г 2      2 I

_r^[2] J1_, 23-

V z 2 ^z 3 ^z 1 ^z 2 J

+ 2 a

Г _2    _2 I

_r ^[2] 29_ , J0_

V ^z 1 ^z 2 ^z 2 z 3 J

п

-----=.

2 Y 0

Приравнивая коэффициенты при одинаковых степенях sin ² ( 9 ) в выражениях (5) и (9), получаем систему нелинейных уравнений относительно волновых сопротивлений звеньев фильтра z_j ( j = Г>

C (z1, z 2, z 3 ) = 0,(10)

C2 (z 1,z2,z3) = 0,

Co (zA, z9,Zo ) — Q6.(12)

^C 1 ^{( z} 1 , ^z 3 ) = 0,

На основании (6), (10)–(12) выводим квадратное уравнение относительно параметра у

V²- ( 2 + 4 Q ⁶ ) у + 1 = 0.

Его решения

C 1 ( z 3 , z 1 ) = 0.                                               (20)

Выражая первый аргумент C1 из (18) и (19), получаем две одинаковые зависимости z 1 (z3) и z3 (z1). Если предположить, что система уравнений (17), (18) имеет хотя бы одно решение, то графики функций z 1 (z3) и z3 (z1), построенные на плоскости (z 1, z3), будут иметь по меньшей мере одну точку пересечения, располагающуюся на линии z 3 = z 1.                                                       (21)

Абсцисса и ордината данной точки задают искомое решение уравнений (17), (18). Таким образом,

V(±) = 1 + 2Q6 ± 2Q371 + Q6 = (71 + Q6 ±Q31

удовлетворяют условиям:

у(-)=^(+^ ,(14)

0 <у(-) ^1, V(+) ^1.(15)

Исходя из определения (8) величины у , можно выразить волновое сопротивление центрального звена фильтра z ₂ через волновые сопротивления крайних звеньев z ₁ , z ₃ :

1 zz z 2 =-р-J-3.                                    (16)

V у ^z 0

если задача синтеза трехзвенного ступенчатого фильтра Баттерворта разрешима, то хотя бы одно ее решение соответствует симметричной конфигурации фильтра, в которой крайние звенья имеют одинаковые волновые сопротивления.

Производя замену (21), можно привести (18) к уравнению четвертой степени относительно неизвестной z ₁ :

2 z 0 z 2 :р-(2 C1 + C2) = yajz 1 + z 4 = 0 с коэффициентами j =o ao =-V z 4, a1 =-2 Tvz3, a2 = 0, a3 = 2 TVz 0.

С учетом (7), (16) можно записать систему уравнений (10)–(12) следующим образом:

Легко показать, что при условии (21) левые части уравнений (17), (18) связаны соотношением

^C 1 =

C l = 4

- 6 - 2 G

+

+ G1

г ( -2 .2      .4 A

■ И z o z o _ш z o

,2’2,V 2 2 + к z 1 z 3    z 1 z 3 7

z ₁ z ₃

z ₁ z ₃

zo z 1 z 3 J.

= 0,

V

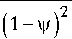
( 2 C 1 + C 2 ) 2 .

Тем самым одни и те же значения волнового сопротивления z ₁ одновременно обращают в тождества уравнения (17), (18).

2. Решение задачи синтеза фильтра

2 с + C o =¹

- 6 - 2 G

; [ 2 ]    1 z o   1 z o

Воспользуемся решением Декарта – Эйлера уравнения четвертой степени [2]. Введем обозначения:

+

к

Z o

3 7

11 2 3 4 p — a     a^ao +   a^a-)      a ,

^{0   0} 4 ¹³ 16 ²³ 256 ³

+ 2 а^[1-Л — i + J к ^z 3 J

к

z

zz у“T, V о ,”1 + ,,

^z 1     ^z 3 ^z 3 J

■   1- 2 -

z ₀

z ₁ z ₃

— 0.

Очевидно, что система (17), (18) инвариантна относительно замены z 3 о Z 1 . Запишем уравнение (17) двумя способами:

P 1 = ^a 1   2 ^a 2 ^a 3 ⁺ 8 ^a 3 , ₽ 2 = ^a 2   8 ^a 3 ^.

Решения уравнения (22) имеют вид:

z 1,1 = 7 y 1 ⁺ T y 2 ^- sign ( ₽ 1 ) 7 y 3

-

4 ^a 3 ,

^z 1,2 = ^ ^- T y 2 ⁺ sign ( ₽ 1 ) 7 y 3 ^- 4 ^a 3 , ^z 1,3 = ^- 7 y 1 ⁺ T y 2 ⁺ sign ( P 1 ) 7 y 3 ^- 4 ^a 3 ,

z i,4 =- 441 ^- T y 2 - sign ( ₽ 1 ) V y 3 - 1 ^а з .           ⁽²⁸⁾

Здесь y j ( j = 1,3) - решения кубичного уравнения 2

^ + y3 = 0, j=0

где

1   91

50 =— 77₽2, 51 =— 7₽0 + ту₽2, §2 = -₽2-(29)

64           4    162

Величины y j ( j = 1,3) задаются соотношениями (решение Кардано [2]):

У 1 =П 1 +П 2 ^--⁵ 2 ,

³                                           (30)

У 2,3 = ^- 2 ⁽ П 1 + П 2 ) ± i ⁽ П 1 — П ) - 3 § 2 .

Здесь

1 П1,2 = 3-2т0 ±^ , (31) 1213 ^ = T +T , 4 027 1 (32) T0 = 50 -35152 + 2752, (33) T1 =51- 3 52. (34) С учетом (23) формулы (24), (29), (32)–(34) дают Po = -16v2-4, P1 =Vv(v-2)z3, 32126 P2 = -2vz0 , 50 = -64v(v-2) z0, 324        32 51 = v z0, 52 =   - vz0, 16             4 To = 116v(v-1)z0, T1 = 0, 11   2 ^= t =     v (v-1) z . 4 0 1024            0 (35) Согласно (31), (35), П1,2 = 31T0 [-1 ± sign (T0 )]. На основании (35) имеем z2 9 v(v-1) 03 n1,2    2\]    4    [ 1 ± sign(v 1)J, или

[- z2 3 1 ^{v(v — 1 )}

П = i 2 v 2

[ 0 ( v> 1 ) ,

[0 (v< 1), n2 = 1 z0 3Iv(v-1)

[ ^- 2 \    2

( v< 1 ) ,

( v> 1 ) .

Тем самым

П 1 +П 2

z ² 3 1 ^{v(v -1 )}

- 2 v ( v

П 1 -n = sign ( v ^-1 ) -2-3 —2

.

Подстановка (36) в (30) дает

У 1 = 4 [v -4*53,

У 2,з = 4 1v+ 3 ^v(' 2 1 ^{) [ 1} ± ■ Vs sign ( v^-1 ) ] • .

Поскольку величины y ₂ и y ₃ являются комплексно сопряженными:

У 3 = У 2, то

Т У 3 = ( 7 У 2 ) . В соответствии с (35) имеем sign ( в - ) = sign ( v -2 ) .			(38) (39)
Равенства (23), (38), (39) позволяют записать			ре-
шения	(25)–(28) уравнения (22) в виде
[ z11 =< [	лБч +2 Re ( 4у2 ) - Z o Vv" ( v< 2 ) ,		(40)
	7 У ? +2 i Im (7 У 2 ) - -0y	v ( v> 2 ) ,
z 1,2 = 1,2	4^1 - 2Re(Т У 2 )— 204'	v ( v< 2 ) ,	(41)
	yF — -2 i Im (7 У 2 ) - z 0\	v ( v> 2 ) ,
z 1,3 =	- ^1 + 2 i Im ( ^2 ) - z o	W ( v< 2 ) ,	(42)
	- j?1 + 2R e ( 44 ) - z4'	v ( v> 2 ) ,
z 1,4 =	- 471 -2 i Im ( 44 ) - z 0	W ( v< 2 ) ,	(43)
	- 441 - 2Re ( 442 ) - 24'	У^ ( v> 2 ) .

Используя (13), легко убедиться в справедливо- сти соотношения

v^{( + )} ^v^{( + )} - - ^ =

= 2 Q ³ 4 Q ⁹ + 3 Q ³ ± ( 4 Q ⁶ + 1 ) V 1 + Q 6 =

3                 3/2

= ± 2 Q ³ Ы1 + Q ⁶ ± Q ³I = ± 2 Q ³ Iv ' " ) ]

Тем самым

V⁺⁾ |и^{( + )} -1 |

/ F+T

= ± Q V и .

С учетом этого выражения (37) принимают вид:

z 2 П+Ц П+\ I y ( ) = -0 x( _ ) X( _ ) + 2 Q , , 1 4 v v* j.		(44)
y 2 x	± ) 2 2 /1± J ' = — л/и x 4 4И( - ) ± Q ± i V3 Q sign |V( - ) - 1J	(45) .
	В соответствии с (13), (14) и( + ) - 2 Q = , 1   - 2 Q = П-У и , 1   | 1 + 2 Q 4 - 2 Q J1 + Q 6 | = n-y v               J Aj ИК 1       ?D2^ f 1     4 ц-7О^1л	- 1 + Q 61   .
	V V и

-^(-) - z 0 4 Ц-^ккЦ-) +70 +

¹1,1 = 2 V^й     v v ^{и + 2 Q +}

z или

Отсюда

Re ^f аД±Л = -z O^ft^ V J 2V2

X

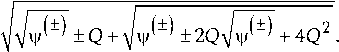
Согласно (15), (40), (44), (49),

+ 2 Q - 4 и⁽ )

> 0,

y 1 ⁺ ) > 0.

Таким же свойством обладает и параметр у 1 ) .

( ± )

Это означает, что y1  является действительной величиной

Re ^f V y^у^ .

Пусть два комплексных числа связаны соотношением a + ib = V A + iB.

Их действительные и мнимые части удовлетворяют условиям:

A = a2 - b2,(46)

B = 2 ab.(47)

Выражая b из (47) и подставляя в (46), получаем квадратное уравнение относительно a ² :

a4 - Aa2

Его решение имеет вид a 2 =1 f A + V A2 + B2 ).

21J

Поскольку действительная часть главного значения квадратного корня из комплексного числа является положительной величиной, то a = I A + A A2 + B2 I.(48)

21J

На основании (45), (48) получаем

V

+

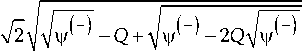
— Г--I

+ 4 Q ² - V.

Таким образом,

J

z 1 1 ) >  0.                                                      (50)

Используя (44), (49), имеем

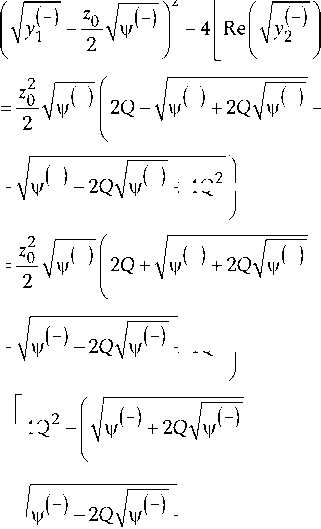
+ 4 Q

4 Q

Л -1

+

x

+

x

+

------I ²

+ 4 Q ² J

+ 4 Q ²

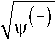
I

2 Q +

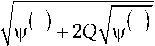
- 1

^- z 0

V

+

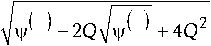
x

и^{( - )}

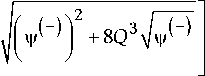
< 0.

Тем самым

УМz0УМ < 2ReIУМ 2                V и, согласно (15), (41),

^{z (} ,2 ) <  0.

В соответствии с (44)

Гм ^z o Гм

A y 1 ⁺ у w⁽) =

Z n     +1 (       +)

= ""04w⁽ ) I vW ) - 2 Q + ⁴ w⁽ )

2 v Mv            v

f+^

' 0 V V .

На основании (49) имеем

<

2Re I УТ MM*

V ² J V2

X ^_VW + Q z^M ) + 2 Q Vv⁽⁺⁾ + 4 Q ² >        (53)

z ₀ 4n+T    +)

>-0-4V 'AAw + Q +w > zqAv •

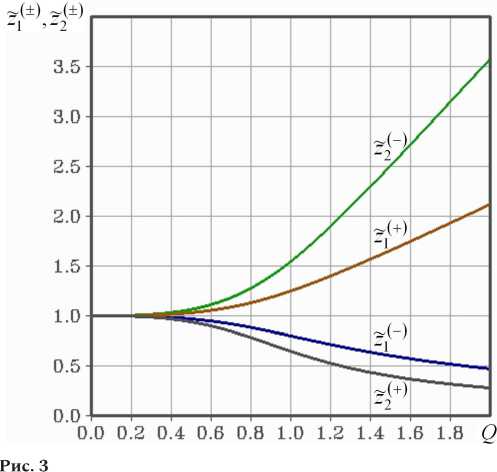
Fig. 4

. ( ± )__z( ± )_ , 1 = ^z 3 =

Принимая во внимание (52), (53), приходим к ус-

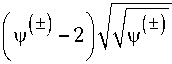
+ 2 Q +

ловию

^2ReIГГ> УТ +zOr TM•

+ V2J Vv^(±) ± Q + W^{(± )} + 2 Q Vv^(±) + 4 Q ² -

Соотношения (42), (54) дают

^z i + 3 ) > ⁰

[V^{+ )} >  2 j •

- 4Ц±) 1   z⁽ ± )-

N ^V , ^z 2 =

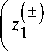
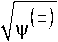
z ₀

Исходя из (54), получаем также

V y ^2^Re I ^ y ^K zo w^{( + )},             ⁽⁵⁶⁾

V J ²

yl +F* ^{2 2R}e I \Z ^y 2 ^{+ )}j ⁺ z0 V V^{1 + )}.                  ⁽⁵⁷⁾

Принимая во внимание первое неравенство (15),

отмечаем, что множитель -sign I w⁽ * - 2 жении (60) для волновых сопротивлений

в выра ^-

J ( - ) z( - ) z ₁ , z ₃

Следствием (40), (41), (56), (57) являются неравен-

ства:

можно заменить на единицу.

Согласно (13), величина w^{( + )} ние w^{( + )} = 2 при

Q = 1/V2•

принимает значе-

z ⁽ + 1 ) > 0, z ¹ + ) < 0 ¹ 1 < и'"< 2 j •                       (58)

Наконец, согласно (43), z1+4)< 0, L1+)> 2 J •                                  (59)

Легко убедиться в том, что подстановка (61) об- ращает выражение

в ноль. Таким

образом, в отличие от множителя sign

Условия (50), (51), (55), (58), (59) позволяют утверждать, что среди всех решений (40)–(43) уравнений (22) действительными положительными являются zli , z1"1) при 11  2 j • В соответствии с (16), (21), (40), (42), (44), (49) симме- тричные решения задачи синтеза трехзвенного ступенчатого фильтра Баттерворта задаются соотношениями:

произведение sign

- 2 Q является

непрерывной функцией Q . Очевидно, что этим ( + )     ( + )

свойством обладают и решения z ₁ , z ₃ задачи синтеза фильтра, определяемые формулой (60). ( - )            ( - )

Что касается функций z 1 ⁷( Q ) и z 3 ⁷( Q ) , то их непрерывность также не вызывает сомнений.

На рис. 3 представлены зависимости нормированных волновых сопротивлений звеньев фильтра

, ,    _z ⁽ ± )

z j "*= j - ( j = 1,2 ) ^z 0

от параметра Q . Как следует из графиков, при лю- ( ± )     ( ± )

бых значениях Q величины z 1 , z 2 удовлетворяют условиям:

z ^{( - ) z} 1

^z 0

z(-) z(+)\z z 2 , z 1    z 0

Z ^{( + )}

z 2 .

Заключение

Таким образом, задача синтеза трехзвенного ступенчатого СВЧ-фильтра Баттерворта имеет два симметричных решения. Этим решениям соответствуют конфигурации фильтра с низкоомным и высокоомным центральными звеньями.