Симметрийный анализ уравнения типа Беллмана

Уравнение Беллмана [1] является одним из основных инструментов теории оптимального управления и динамического программирования. Оно широко используется в технических науках и экономике, является ключевым элементом многих алгоритмов машинного обучения и искусственного интеллекта.

Одной из актуальных задач теории управления является задача оптимальной коррекции траектории движения материальной точки при малых возмущениях. Согласно подходу академика Ф.Л. Черноусько [2, 3], исследование таких процессов может быть сведено к решению краевой задачи для нелинейного уравнения в частных производных второго порядка (уравнения типа Беллмана).

Характерной особенностью уравнения, существенно усложняющей его аналитическое исследование, является его многомерность: даже в простейшей постановке оно содержит три независимые переменные – временную и две пространственные. Одним из эффективных методов анализа нелинейных уравнений является групповой анализ [4]. Данный метод позволяет не только установить ряд качественных свойств уравнения, но и найти его частные решения уравнения. Его преимущество при решении задач оптимального управления лазером, например, подробно описаны в работе [5]. Групповой анализ применяется и в задачах об оптимальном управлении пограничным слоем [6].

В работе рассматривается уравнение с квадратичной нелинейностью, которое является частным случаем дифференциального уравнения Беллмана, вида [7, с. 259]

u t u x - f( t ) u x u yy - g( t ) ( u y ) ² = 0, ⁽¹⁾ где f( t ) и g( t ) - произвольные функции, f( t ) ^ 0, g( t ) ^ 0. Решается задача групповой классификации относительно функций f( t ) и g( t ) по допускаемым этим уравнением однопараметрическим группам Ли точечных преобразований. Также строятся некоторые инвариантно-групповые решения уравнения (1).

Следуя работе [8], в дальнейшем используется обозначение д/д t = д _t .

• 1.    Групповая классификация

Будем искать для уравнения (1) допускаемую группу преобразований с оператором вида

X = т ( t , x , y , u ) д _t + Z ( t , x , y , u ) д _x + Z ( t , x , y , u ) д _y + n ( t , x , У , u ) д _u .                   (2)

Действуя вторым продолжением оператора (2) на уравнение (1), получаем определяющее уравнение

X f I utu x ^{- f(} t ) u x u yy ^- g⁽ t ) ( ^uy ) ²

= 0.

Расщепляя его по независимым переменным u_x , u_y , u_xy , … , приходим к довольно громоздкой определяющей системе, большая часть уравнений которой легко решается. В результате находим

т = т ( t ), £ = C 1 x + C 2 где C i - произвольные постоянные, i = 1,... нутся лишь следующие два уравнения:

,    Z = C 3 y + C 4 ,    n = C 5 и + C 6 ,

,6, а из нерешенных в определяющей системе оста-

< g T '+ g' T = ( 2 С 3 - С 1 ) g, f т '+ f' т = 2 С ₃f.

Таким образом, задача групповой классификации сводится к решению классифицирующей системы на функции f( t ) и g( t ) , построенной на основе системы (4)

< g(t) w'(t)+ g'(t)w(t) = (2A - B) g(t), ft )w'( t) + f'( t )w( t) = 2 A f( t), где A, B - произвольные постоянные, w(t) - произвольная функция. Поскольку f(t) Ф 0, g(t) Ф 0, разделим первое уравнение системы на g(t) , а второе – на f(t) . Переходя к логарифмам функций f( t) = ln|f( t )|,     g( t) = ln|g( t )|, имеем систему

'w'( t ) + g'( t )w( t ) = 2 A - B , w'( t ) + f '( t ) w( t ) = 2 A .

Вычитая первое уравнение из второго, приходим к соотношению (f' - g')w = B .

Случай 1 . Пусть ^f' Ф g', тогда из (6)

w =

B

ˆ.

f' - g'

Вычисляя производную w( t ) и подставляя в систему (5), получаем уравнение B f ' ( f' - g' ) - B ( f "-g'' ) = 2 A ( f' - g' ) 2 ,

которое связывает функции fˆ( t ), gˆ( t ) и постоянные A , B .

Если f(t) и g(t) - произвольные функции, то условие (7) выполняется при A = B = 0. Возвращаясь к системе уравнений (4), получаем, что С1 = 0, С3 = 0, т = 0. Следовательно, уравнение (1) допускает оператор (2) с координатами т = 0,    £ = C2,   Z = C4,   П = C5 и + C6.

Пусть f( t ) и g( t ) удовлетворяют условию (7). Выясним их общий вид, когда A Ф 0, B Ф 0. Обозначим

А =— ,   h( t ) = f( t ) - g( t ),

B причем h'(t) Ф 0. Условие (7) перепишется в виде f'h'- h'' = Ah'2, откуда f = Ah + lnh'+ In b,     g = (A -1) h + lnh'+ In b, где b - произвольная постоянная, b Ф 0. Получаем общий вид функций f(t) и g(t), которые удовлетворяют условию (7) в параметрическом виде:

f = b h' e ^{A h},      g = b h' e ^{( A - 1 ) h}.

С A„

Подставляя функции f( t ) и g( t ) в систему (4), находим т = ——, C ₃ = — C . Следовательно, в h'( t )    ³ 2 ¹

этом случае уравнение (1) допускает оператор (2) с координатами

Математика

т = С ), £ = C 1 x + C 2 , Z = - С 1 у + C 4 , П = C 5 и + C 6 .

Случай 2 . Пусть f' = g', тогда функции линейно зависимы: g( t ) = k f( t ), где k Ф 0 - произвольная постоянная. Из системы (4) получаем С 1 = 0 и находим функцию т , а координаты допускаемого оператора (2) будут иметь вид

2 С 3 J f( t ) dt + C 7

f( t )

,

£ = C 2 ,    Z = C 3 у + C 4 ,    П = C 5 и + C 6 .

Таким образом, доказана справедливость следующего утверждения.

Утверждение. В зависимости от вида функций f( t ) и g(t) уравнение типа Беллмана (1) допускает четырех-, пяти- или шестипараметрическую группу Ли точечных преобразований. А именно,

• 1)    если f( t ), g( t ) - произвольного вида, f( t ) Ф 0, g( t ) Ф 0, то уравнение (1) допускает четырехпараметрическую группу Ли G 4 с операторами

^G 4 :       X 1 =Э x , X 2 = ^д y ,    ^X 3 =Э u ,     ^X 4 = и Ә u ,

• 2)    если f = b h' e ^{A h},g = b h' e ⁽ ^ 1 ) ^h, где h( t ) - произвольная функция, h( t ) Ф сonst, b , A -произвольные постоянные, b Ф 0, A Ф 0, то группа Ли G 4 расширяется до пятипараметрической оператором

1             ^

X =---o, + x дг +—yo,,

⁵ h'( t ) ^{t x} 2 ^y

• 3)    если g( t ) = k f( t ), где k Ф 0 - произвольная постоянная, то группа Ли G 4 расширяется до шестипараметрической операторами

  1 f( t )

  
  

  6 = ~-----д, + у д

  ⁶       f( t )       ^t

  
  

• 2.    Инвариантные решения

Построим некоторые инвариантные решения уравнения (1). Общий инвариант для оператора X2 есть функция I(t, x, и). Анзац на решение и = ^(t,x) приводит к двум возможным инвариантным решениям уравнения (1) вида и = ^( t), и = ^( x).

Для абелевой подалгебры с базисными операторами X1, X2 инвариантное решение тоже имеет вид произвольной функции от переменной x: и = ^(x). Если взять за основу решения инвариант линейной комбинации операторов aX2 - b X1, где a, b - произвольные постоянные, то, предполагая, что решение имеет вид и = ^( t, ax + by), получим линейное редуцированное уравнение a?t = ab 2f( t )pzz + b 2g( t )pz, где z = ax + by.

Рассмотрим двумерную подалгебру L2 ={X1 + aX3,X2 + bX3}, где a,b - произвольные постоянные. Из общего инварианта имеем анзац на решение и = ax + by + ^( t), подставляя который в уравнение (1), получим редуцированное уравнение a^ = b 2g( t), которое легко интегрируется. В результате находится инвариантное решение в виде b2

и = ax + by + J g( t ) dt + C , где C – произвольная постоянная.

Камалетдинова Д.И.,                        Симметрийный анализ уравнения типа Беллмана

Лукащук В.О.

Рассмотрим другую двумерную подалгебру {X1 + aX4, X2 + bX4}, из общего инварианта которой имеем анзац на решение вида u = eax+Ьу?( t). В результате решения редуцированного урав- нения получаем инвариантное решение ax +Ьу+Ь 2 J| f(t)+g^ J dt u = Ce y a 2 , где C – произвольная постоянная.

Для оператора X ₅ , в случае параметрической зависимости функций f и g, анзац на решение

имеет вид и = ? xe <

h ( t ) , ye

Mi ( t ) ^

, а уравнение (1) редуцируется в уравнение с двумя переменны-

ми

z^z + M V^z^v + bPzPvv + bvV = 0,

Mh ( t )

где z = xe ^{- h (} t ) , v = ye ² .

В случае линейной зависимости функций f и g для оператора X ₅ получаем инвариантное решение и = ? ( x , у ) , где ? удовлетворяет редуцированному уравнению

?yy?x + к? = 0.

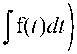
а редуцирован-

Для оператора X 6 инвариантное решение ищется в виде и = ?

ное уравнение меньшей размерности по пространству имеет вид

4 kz 2gz2z +(6 z - 1)PzPx + 4 z 2фх^2 = 0, где z =

Заключение

В работе исследованы симметрийные свойства уравнения типа Беллмана. Установлено, что в случае произвольного вида функций от времени, стоящих при первых производных по пространству, допускаемая группа преобразований для исследуемого уравнения является четырехпараметрической. Если функции связаны через параметрическое соотношение, то группа расширяется до пятипараметрической. В случае, когда функции пропорциональны, группа расширяется до шестипараметрической. Для некоторых допускаемых операторов и на их двумерных подалгебрах построены инвариантные решения, которые могут быть использованы в дальнейшем, например, при решении уравнения (1) с помощью численных методов для тестирования вычислительных программ. С помощью ряда операторов удалось понизить порядок уравнения (1) и выписать соответствующие редуцированные уравнения.