Simulation and Tuning of PID Controllers using Evolutionary Algorithms

Published Online October 2012 in MECS

PID Controllers find a large scale application in control of the nuclear power plants. In a nuclear power plant, the level control of the Process equipments like the Deaerator, Condenser Hot well is of high importance in determining the equipment safety, efficiency and the downtime of the plant. For the implementation of level controllers, tuning of the controller parameters is found to be a tedious job and often it is very difficult to precisely zero in on a certain combination of the PID parameters. A conventional PID controller tuned with fixed parameters may usually derive poor control performance when it comes to system complexities [1,2]. Since the gain and the time constants of the system change with the operating conditions, the conventional PID controllers result in sub-optimal corrective actions and, hence, require frequent tuning adjustments. This necessitates the development of tools that can assist engineers to achieve the best overall PID control for the entire operating envelope of the given process.

Methods such as Neural networks, Optimization algorithms are being used to confront the system complexities[3, 4]. Optimization algorithms have proved to be better off than the Neural network counter parts in their ease of implementation. Evolutionary algorithm is one of these Optimization algorithms which find application in control engineering. Genetic algorithms (GA), a sub set of Evolutionary Algorithms, are powerful optimization algorithms that work on a set of potential solutions, which is called population.GA finds optimal solution  through  cooperation and competition using the  potential  solutions. These algorithms are highly relevant for industrial applications, because they are capable of handling problems with nonlinear constraints, multiple objectives, and dynamic components – properties that frequently appear in real-world problems [5].

Further in this paper, Section 2 discusses about PFBR and its Operator Training Simulator. Section 3 discusses deaerator in PFBR with its level control philosophy. Section 4 presents the mathematical model of the deaerator. Section 5 elaborates on the PID controller tuning with traditional techniques followed by a section on Genetic Algorithm. Section 7 presents the GA implementation. Section 8 presents the Experimental results on PFBR OTS platform under steady state and transient condition. Section 9 shows the Conclusion of the experiment.

• II.    PFBR and PFBR Operator Training Simulator

Prototype Fast Breeder Reactor (PFBR) is a 500 MWe capacity, pool type reactor utilizing sodium as the main heat transport medium. The reactor core consists of fuel sub assemblies made up of (Uranium, Plutonium) Mixed Oxide Fuel. The Heat transport system consists of Primary sodium circuit, Secondary sodium circuit and Steam water system (Refer Fig.1). Steam and water system adopts a reheat and regenerative cycle using live steam for reheating. Energy transfer is done through Electrical System using Turbo alternator set of capacity 500 MWe .

A high fidelity Full Scope Operator Training Simulator is being developed at IGCAR for training the

PFBR Operators. It comprises of Simulation Computers, Control Panels, Operator Information Consoles, Input/ Output systems, Instructor station and has a horizontal coverage of all the main systems of the plant. The simulated systems include Neutronics system, Primary Sodium system, Secondary Sodium System, Decay Heat Removal System, Core Temperature monitoring System, Steam Water System, Electrical system, Fuel Handling System [6].

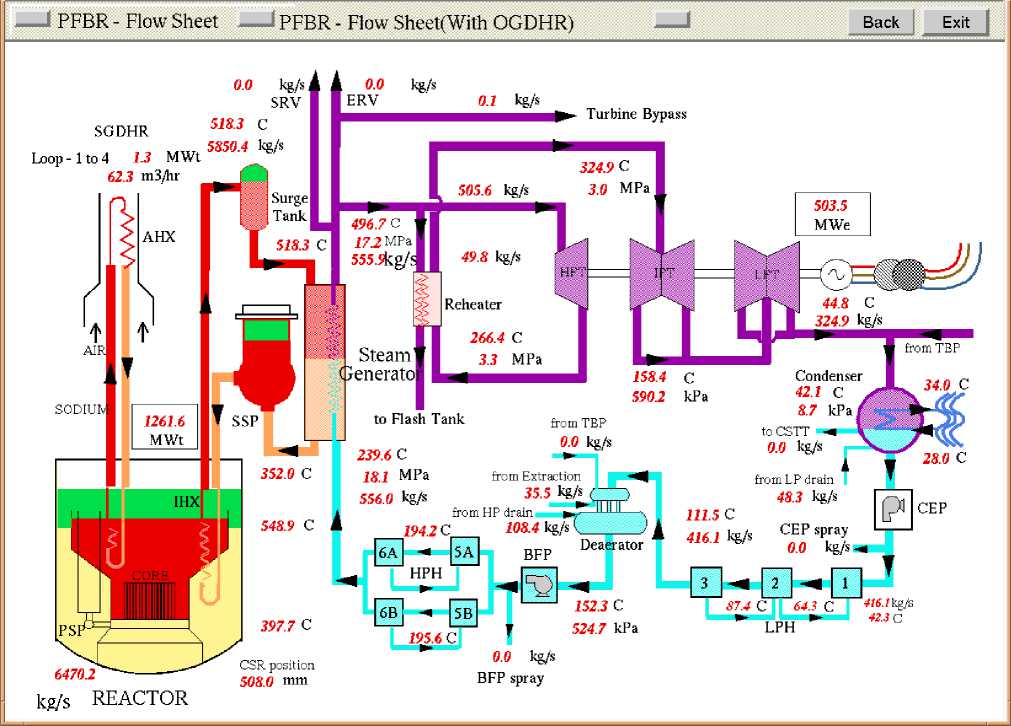
Fig 1. PFBR Flow sheet

• III.    Deaerator and its storage tank level control

The presence of oxygen and the other active gases dissolved in the condensate water cause the corrosion of the system, resulting in the plant life shortening. Deaerator is the equipment introduced in the steam cycle to remove the non condensable gases from the feed water before it enters the Steam Generator.

In PFBR, the deaerator located in the feed water system, accepts the condensate water from the Low Pressure Heaters (LPHs) to heat and deaerate the water and supply it as Feed water to the suction of Boiler Feed Pumps (BFPs) [7]. The BFPs further pump the feed water to the two parallel banks of High Pressure Heaters (HPHs) before it enters the Steam Generator. The deaerator is mounted on a storage tank which provides the Net Positive Suction Head (NPSH) of the BFPs. (Fig 2.) The deaerator storage tank also acts as a receiving vessel for the HPH drains and the BFP leaks-offs and pump recirculation.

The three inputs to deaerator are: Condensate water from the condenser through the previous low pressure heaters, w c , extraction pegging steam from the intermediate pressure turbine (IPT), w e , and the drains from the next set of high pressure heaters, w d . The central pipes link the deaerator and the storage tank and equalizers are provided to balance the pressures of the two tanks. The suction pipe is used to establish the suction head for the feed water pumps.

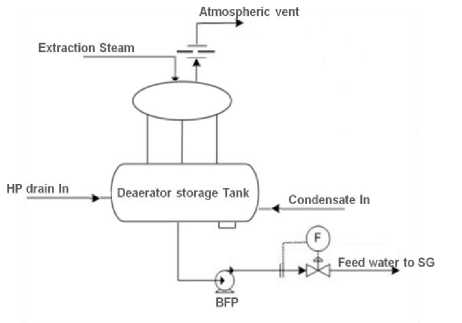
Fig. 2: Deaerator

In PFBR Operator Training Simulator, the normal level control of Deaerator storage tank is accomplished by controlling the Condensate flow from the Condenser Hot well to the Deaerator. This is done by regulating the Control valve (DALC) on the main condensate line to deaerator using a PID controller, which senses the level in the deaerator storage tank and accordingly delivers the control signal to the actuator of the control valve (Fig 3).

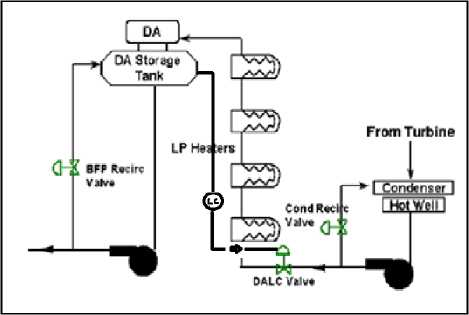
Fig. 3: PI Diagram of Deaerator level Control

• IV.    Deaerator Model

Tuning the controller to achieve good response is imperative. However, the effectiveness of the designed controller in terms of the system requirements is greatly governed by the accuracy of the system model. Hence, it is desirable to model the dynamics of the process near the operating point by simpler models for the purpose of controller design and also for process analysis.

A mathematical model of the deaerator is proposed. To establish the dynamic model which describes the relation between the storage tank level and the flow rates, the analogy of electrical resistance and capacitance is introduced as shown in Fig 4.

In this figure, H is the level in steady state and h is the deviation from H and Q is the normal flow rate and qi and qo denote flow rate deviation from the steady state inlet and outlet flow rates, respectively [8].

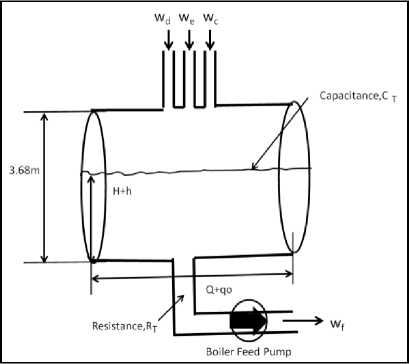
Fig. 4: Deaerator model

The variation of the condensate in the storage tank during dt is

Crdh = (qi - qo)dt                              (1)

Where C T is the tank capacitance defined as

variation of condensate volume.m-C- =------------------------------------------- " variation incondensate level instorage tank.m

Therefore, the tank capacitance is the surface area of the condensate as in the Fig 4. The tank resistance at the outlet, R T , is defined as

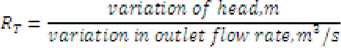
However, the head has relation to the flow rate in a non-linear manner. The non linearity is due to the circular vertical cross section of the tank. With the assumption that the variations are small, linearity could be obtained around the steady state point. Then the resistance at the outlet is

dH dh dQ"" Ro

So at steady state,

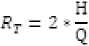
From equations, the rate of change of head is found to be

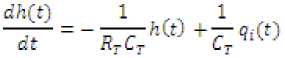
Converting the above equations in s-domain at steady state, results in the following transfer function:

H(s) 0.011Qi(s) * 1 + 0.022s

• V.    Tuning of PID Controllers

Today, the PID Controllers are put in use in more than 90% of the control systems because of their simplicity and robustness [9]. The effectiveness of the PID controller action is wholly dependent on the gains of the PID controllers. In general a classical PID control system can be depicted as shown in the figure in which the input-output relation of the PID Controller is expressed as

/dei

u=^e+(- edt + Td(-

Jp                                    (8)

Where u is the control signal, e is the error signal, and Kp ,Ti and Td, are the proportional gain, integral time and derivative time.

In the transfer function form it is,

„   _ Kps'+Kps+K]

P[D~      :                                 (9)

Proportional gain, Kp will have the effect of reducing the rise time but never eliminate the steady state error. The integral gain, Ki will have the effect of eliminating the steady state error, but it may make the transient response worse. The derivative gain, Kd will have the effect of increasing the stability of the system, reducing the overshoot, and improving the transient response.

The design of control system is an attempt to meet a set of specifications which defines the overall performance of the system in terms of certain measurable quantities. These measurable quantities are referred as performance indices like Integral Absolute Error (IAE), Integral Square Error (ISE), Integral Time Absolute Error (ITAE) and Mean Square Error (MSE). If performance indices increases, control system can perform poorly and even become unstable. So the controller parameters need to be tuned to achieve good control performance with the proper choice of tuning constants. Over the past years, Controller tuning was performed by numerous conventional methods like the Ziegler Nichols Ultimate Gain method, Trial and Error method, and Cohen-Coon method.

In this paper, the controller tuning is done using the Critical gain and Critical period method (Ziegler Nichols Ultimate Gain method,) and also with the non-conventional method based on Evolutionary Computation.

• A. Traditional Technique for PID Controller Tuning

The traditional technique for PID tuning employed here is the Ziegler-Nichols PID tuning rules based on critical gain and critical period [10].

For the Deaerator model,

H(s) 0.011

Qi(s) “ 1 + 0.022s the critical gain Kc, at which the output of the system exhibits sustained oscillations and the corresponding period Pc, are experimentally determined[11].

The values of Kc and Pc are 0.22 and 0.12 respectively. Considering these two parameters, the PID parameters Kp, Ti, and Td are estimated according to the formula:

K p = 0.6K c , T i = P c /2 , and Td= P c /8

Based on the application of Ziegler Nichols PID tuning method we get the PID tuning parameters as

K p = 0.1 , K i = 1.0, K d = 1.0

With these values of the gains of the PID, the unit step response of the tuned control system is plotted and discussed later in the paper.

• VI. Genetic Algorithm

Genetic algorithm is a powerful search algorithm that performs an exploration of the search space that evolves similar to the evolution in nature. GAs use probabilistic transition rules instead of deterministic rules, and handle a population of potential solutions known as individuals or chromosomes that evolve iteratively (Fig 5). Each iteration of the algorithm is termed as a generation. The evolution of solutions is simulated through a fitness function and genetic operators such as reproduction, crossover and mutation. The fittest individual will survive generation after generation; while also reproducing and generating offspring’s that might be stronger [12]. At the same time, the weakest individuals disappear from each generation.

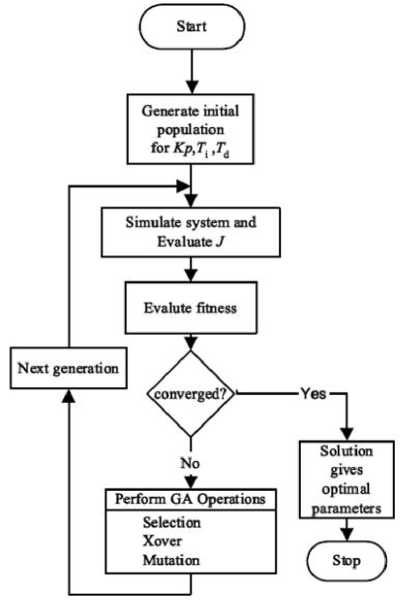
Fig. 5: GA Implementation

A genetic algorithm is typically initialized with a random population consisting of between 20 and 100 individuals. This population (mating pool) is usually represented by a real-valued number or a binary string called a chromosome. Fitness value is a measure of response of the chromosomes to the objective function. The fitness of each chromosome is assessed and a survival of the fittest strategy is applied. In this paper, the magnitude of the error is used to assess the fitness of each chromosome. There are three main operators for a genetic algorithm – Selection, crossover and mutation.

• A.    Selection

The fitness value of the chromosomes is used in the selection process to provide bias towards fitter individuals. Just like in natural evolution, a fit chromosome has a higher probability of being selected for reproduction. The probability of an individual being selected is, thus, related to its fitness, ensuring that fitter individuals are more likely to leave offspring.

• B.    Crossover

Once the selection process is complete, the crossover algorithm is initiated. The crossover operations swap certain parts of the two selected strings in a bid to capture the good parts of old chromosomes and create better new ones. The crossover probability indicates how often crossover is performed.

The different crossover techniques are the Single Point Crossover, Two Point Crossover, Uniform Crossover etc are defined for different types of chromosome encoding.

• C.    Mutation

Mutation is the occasional random alteration of a value of a string position. It is considered a background operator in the GA. The probability of mutation is normally low because a high mutation rate would destroy fit strings and degenerate the GA into a random search. Once a string is selected for mutation, a randomly chosen element of the string is changed or ‘mutated’.

• VII.    GA Based Tuning of the Controller

In this method, the GA is used to search for the optimal PID parameters that minimize the error when the process is in steady state. Therefore, the parameter tuning problem of PID controller using GA can be considered by selecting the three parameters such that the response of the system is desired (Fig.5). For the PID controller design, it is ensured the controller settings estimated results in a stable closed loop system [13,14].

• A.    Initialization of Parameters

Initialization of certain parameters, like the Population size, Number genes in a chromosome, Crossover probability, Mutation probability, Selection probability, Number of generations, is done at the first stage of GA implementation.

The encoding used for the population is real encoding where every gene in the chromosome represents the random value of the parameter to be optimized. The GA parameters are listed in Table 1.

Table 1: GA Parameters Initialization

POPULATION SIZE	20
NUMBER OF GENES	3
CROSSOVER PROBABILITY	0.8
MUTATION PROBABILITY	0.025
TOURNAMENT  SELECTION PARAMETER	0.75
VARIABLE RANGE	-100,100
NUMBER OF GENERATIONS	100

• B.    Objective Function

The objective function considered is based on the error criterion. A number of such criteria are available. In this paper controller’s performance is evaluated in terms of the Mean Square Error (MSE) criteria. The error criterion is given as a measure of the performance index given by the equation. The fitness value of each chromosome is defined as the reciprocal of the magnitude of the objective function. Thus the optimum values of parameters minimize the error, that is, maximizes the fitness function.

'mse =       * *^

Fitness value =

' L45E                         (11)

• C.    Termination Criteria

Termination of GA can take place either when the maximum number of iterations or generations gets over or with attainment of satisfactory fitness values. Here, the termination criteria is defined as the maximum number of generations as 100.

• D.    Selection, Crossover and Mutation

Tournament Selection method is used. In tournament selection, a number of individuals are chosen randomly from the population and the best individual based on the fitness value, is selected as the parent. This process is repeated as often until there are sufficient individuals to choose. These selected parents produce uniformly random off springs. The parameter for tournament selection is the Tournament Selection Parameter which is defined as 0.75.

For real value encoded GAs, the different crossover methods are Uniform Crossover, Arithmetic Crossover, and Heuristic Crossover etc. In this study, Arithmetic crossover is implemented on the selected chromosomes. Arithmetic crossover operator linearly combines two parent chromosome vectors to produce two new offspring according to the equations given below:

Offspring1 =a* Parent1 +(1-a)* Parent2

Offspring2 =(1–a)* Parent1 +a* Parent2

Where, ɑ is a random weighting factor (chosen before each crossover operation).

Mutation operators for real value encoded GAs are Boundary Mutation, non uniform mutation, Uniform mutation and Gaussian mutation. Of these mutation operators, the boundary mutation operator is implemented. A Boundary mutation operator replaces the value of the chosen gene with either the upper or lower bound for that gene (chosen randomly).

• VIII.    Experimental results

The proposed GA method was applied to the level control system of the deaerator model for minimizing the MSE error criterion for 100 generations. For each generation the best of the population, the Kp, Ki and Kd parameters, was chosen and plotted. The variation of the PID parameters is shown in Fig 6.

From the application of PID tuning based on GA we get the PID tuning parameters as

K p = 14.2853, K i = 38.0604, K d = 70.488

Generations

Kd Value

Generations

Fig. 6: PID gain variation with generations

The response of the PID controller with the gain parameters tuned using Ziegler –Nichols (ZN) and GA for a unit step input is shown in the Figure 6.It is seen from the above plot that the settling time with the parameters tuned using GA the settling time of the response is 70 secs as compared to that of the ZN tuned controller, whose settling time of response is 220 secs . Thus, the GA tuned controller outperforms the ZN tuned controller with its fast response.

With the optimum PID parameters obtained from the GA implementation, the PID controller for level control of deaerator in PFBR Operator Training Simulator was configured and its performance was studied under steady operation as well as under a transient condition of the power plant.

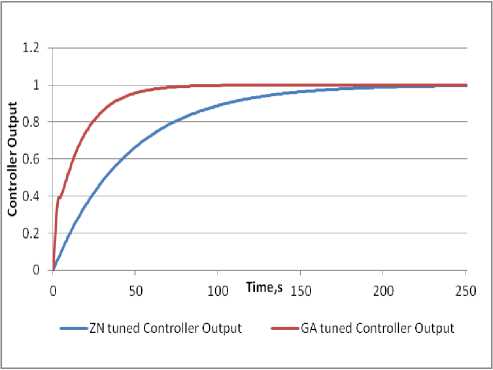
Fig. 7: Controller response to Unit Step as input

• A.    Under steady state condition:

The controller’s behavior is examined under the steady state operation of the plant. Under this condition, the deaerator level control valve maintains the steady value of normal level of water in the storage tank. This, it does by throttling the valve as demanded by the controller. The controller response is found to be satisfactory.

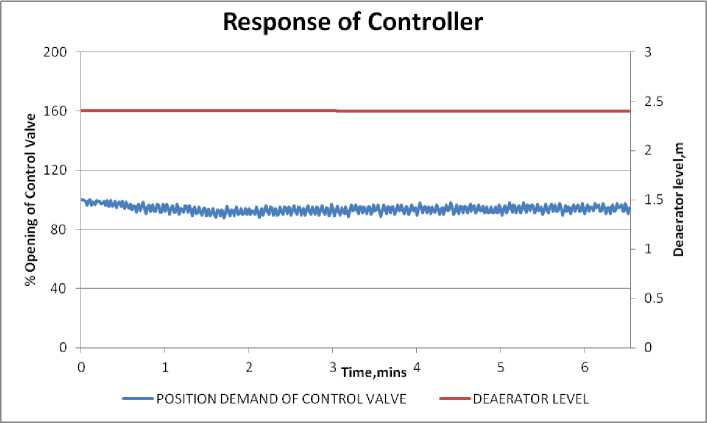
Fig. 8: Controller response in Steady state conditions

• B.    Under transient condition:

The controller’s behavior is studied under the transient “Tripping of one Condensate Extraction pump (CEP) and standby does not take over”. Under this event, because of the trip of the one of the two CEPs, the deaerator level starts decreasing. The level decreases to a value where it initiates the power setback, that is, 60% power condition in the plant. The decrease in deaerator level continues until the 60% flow at the exit of deaerator is established by the feed water control stations[15,16].

Subsequently, the level controller tries to maintain the level of water in storage tank at the normal value of 2.4m by throttling the valve accordingly. The behavior is shown in the Fig 9.The controller response under this scenario is acceptable.

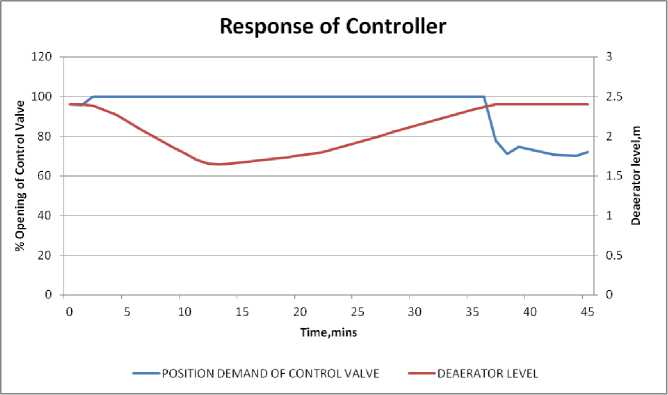
Fig. 9: Controller response under one CEP trip scenario

• IX.    Conclusion

The experimental results show that the GA provides optimum settings of parameters of PID controllers over that provided by the traditional tuning techniques. Hence the accuracy and efficiency of the system performance can be maintained. The performance of the controller with the optimum PID gain settings on PFBR

Operator Training Simulator Environment showed better tracking of the error and also a robust behavior. In conclusion, the performance of the Deaerator level control system improved greatly in terms of steady state response as well as transient response with the GA tuned controller. GA based tuning certainly shows a great promise to replace the cumbersome manual tuning methods.

• [1]    Salami, M. and Cain, G., “An Adaptive PID Controller Based on Genetic Algorithm Processor” Genetic Algorithms in Engineering Systems: Innovations and Applications, 12-14 September, Conference Publication No. 414, IEE (1995).

• [2]    Asriel, U.L. and Narendra, K.S., “Control of Nonlinear Dynamical Systems using Neural Networks-Part II: Observability, Identification and Control”, IEEE Transactions on Neural Networks, Vol. 7, No. 1, January (1996).

• [3]    Mistry,S.I.,Chang,S.L and Nair, S.S., “Indirect Control of a Class of Non-linear Dynamic Systems”, IEEE Transactions on Neural Networks, Vol. 7, No. 4, July (1996).

• [4]    Fabri, S. and Kadirkamanathan, V., “Dynamic Structure Neural Networks for Stable Adaptive Control of Non-linear Systems”, IEEE Transactions on Neural Networks, Vol. 7, No. 5, September (1996).

• [5]    Jan, J.A. and Sulc, B., “Evolutionary Computing Methods for Optimizing Virtual Reality Process Models”, International Carpathian Control Conference ICCC 2002, Malenovice, Czech Republic, May 27-30 (2002).

• [6]    Scope Document on PFBR Operator Training Simulator - PFBR/ 08610 / DN / 1000 /Rev A, (2003).

• [7]    Design Notes on Feed Water System -PFBR/43000/DN/2050.

• [8]    Kyung Youn Kim and Yoon Joon Lee,” Fault Detection and Diagnosis of the Deaerator Level Control System in Nuclear Power Plants”, Journal of the Korean Nuclear Society, Volume 36,Number 1,pp.73-82,February,2004.

• [9]    Sung, S.W., Lee, I.-B. and Lee, J., “Modified Proportional-Integral-Derivative(PID) Controller and a New Tuning Method for the PID Controller”, Ind. Eng. Chem. Res., 34, pp. 4127-4132 (1995).

• [10]    Ziegler, J.G. and Nichols, N.B., “Optimum Settings for Automatic Controllers”, Trans. Amer. Soc. Mech. Eng., Vol. 64, pp. 759-768 (1942).

• [11]    K Ogata, Discrete-Time Control Systems, University of Minnesota, Prentice Hall, 1987.

• [12]    David E. Goldberg, Genetic Algorithms in Search, Optimization and Machine Learning. The University of Alabama, Addison-Wesley Publishing Company Inc, 1989.

• [13]    T O. Mahony, C J Downing and K Fatla, Genetic Algorithm for PID Parameter Optimization: Minimizing Error Criteria, Process Control and Instrumentation 2000 26-28 July 2000, University of Stracthclyde, pg 148-153.

• [14]    Sadasivarao, M.V. and Chidambaram, M., “PID Controller Tuning of Cascade Control Systems Using Genetic Algorithm”, Journal of Indian Institute of Science, 86, July-August, pp. 343- 354 (2006).

• [15]    Preliminary Safety Analysis Report, Chapter 14 -PFBR Events Analysis Report.

• [16]    Preliminary Safety Analysis Report, Chapter 8 -Instrumentation & Control System.

T.Lakshmi Priyanka: Working as Scientific Officer at IGCAR, Kalpakkam. Interested in Process Modeling and Simulation.