Simulation of metal layers thickness influence on phase velocities of acoustic waves in the piezoelectric plates

Introduction. At the present time the properties of the elastic waves propagating in the thin plate which thickness has the same order as longitudinal and transverse waves lengths in the considered material are studied quite explicitly [1]. There is a large number of pilot and theoretical studies of characteristics of various Lamb elastic waves and SH waves modes in plates from isotropic, piezoelectric and composite materials [2–4].

Metal layer application (metallization) on piezoelectric plates surfaces leading to the electric short circuit of a surface, as a rule, decreases the velocity of acoustic waves propagation [5; 6].

Acoustic waves in piezoelectric plates are a perspective object for the development of microwave resonators and sensors of the next generation. Due to high interest in this issue there appeared many pilot and theoretical studies of acousto-electronic devices on the basis of the piezoelectric plates operating at various modes of elastic waves [7–10]. As a rule, for of elastic waves in devices electrodes (interdigitated transducers, IDT) placed on a plate surface are used.

In devices created on the basis of a single-layer or a multilayer piezoelectric structure, the thickness of electrodes can be comparable to the acoustic line plate thickness. At the same time the precious metals, such as gold or platinum which are often used in sensors for various biochemical applications, have essential values of an acoustic impedance [11].

Therefore, metal layers thickness and mass cannot be neglected. Thus, considering the impact of metal layers on the change of dispersion characteristics of various modes of an elastic wave in the piezoelectric plate is important for the improvement of devices characteristics on similar structures [12].

In this work the computer simulation of load influence in the form of two metal layers on dispersion characteristics of Lamb elastic wave modes in zincum oxide plates (Me/ZnO/Me structure) and aluminum nitride (Me/AlN/Me structure) was executed. These piezoelectric materials have great values of the electromechanical coupling coefficient and considerable values of phase velocities for bulk and surface acoustic waves. Thanks to these properties the considered materials are actively applied when developing various acousto-electronic devices. Aluminum and molybdenum in the form of the thin metalizing film were used as materials for metal layers, that is the metals which are often applied at electrodes production [13]. The choice of two metals with various acoustic impedances also allows to analyse how the material layer acoustic impedance influences the change of phase velocity of various elastic wave modes in an acoustic line.

The executed simulation results can be used when developing various acousto-electronic devices including those used as components of the rocket and space technology electronic base.

Theoretical bases of elastic waves propagation in layered piezoelectric medium. Let us consider the propagation of small amplitude elastic waves in unperturbed by external influences piezoelectric crystal. The motion equation, the electrostatics equation and the state of piezoelectric medium equations have the following form [14]:

^p0 ^U A  ^т AB,B ; D M,M ⁰ ;

E

^T AB = c ABCD ^П CD - e MAB E M ;

D M = ^ MN E N + e MAB ⁿ AB ,

where ρ₀ – crystal density in an undeformed state; U_A – vector of dynamic elastic displacements; τ _AB – tensor of thermodynamic stresses; D_M – electric induction vector; η CD – tensor of small deformations; c_A^E_BCD , e_MAB , ε ^η _MN – elastic, piezoelectric and dielectric constants of the second order.

For elastic displacements and electric potential in the form of plane monochrome waves of small amplitude the set of equations (1) is recorded as Green-Christoffel equation which has to be solved for each layered structure medium [15].

Let axis X ₃ be directed along an outward normal to the layer surface in a working orthogonal system of coordinates and axis X ₁ coincide with the wave propagation direction (fig. 1, а ). The elastic wave propagation in such system has to meet the corresponding boundary conditions.

Boundary conditions, in particular, for the threelayered structure „metal/piezoelectric/metal“ are: equality to zero of normal component of a stress tensor on the „metal/vacuum“ interface; equality of normal component of a stress tensor, equality of displacement vectors and equality to zero of the electric potential wave on the „metal/piezoelectric“ interface [16]:

^’l

3j lx3 = dx j т“|   ;ф“= 0|   ;U"> = U®\ ,.

x з = h                l x з = h                     l x з = h

t(2-= t»>|      ,ф-= 0|      ; t/--)= U»’\, j j lx3 = d2                  lx3 = d2                        lx3 = d2

т(3)|

³j l x 3 = 0

Here d 1 , d 2 and h – thickness of metal overlayer, sublayer and piezoelectric layer respectively.

In this work the d 1 = d 2 condition is met, i.e. metal overlayer and sublayer thicknesses are equal.

Substituting the elastic wave equation in the form of linear combinations of partial waves in boundary conditions:

Ui = Z Cm)a(n)exp [i (kix + k3n)x3 - ®t)] , n (3)

Ф = ^ C4m )a4n )exp [ i (k1 x1 + k3(n) x3 - to t)] , n where the superscript n is equal to the number of partial waves in the corresponding layer, we will recieve a linear equation system - boundary conditions. Equality to zero of boundary conditions matrix continuant (2) which dimension in this case is 20×20 elements allows to calculate phase velocities of the symmetric and antisymmetric modes of the Lamb wave and SH-wave.

Variations of boundary conditions (2) define all types of elastic waves propagating in the three-layered plate. When using isotropic metals and piezoelectric materials of a symmetry group 6 mm for the considered layered structures Me/ZnO/Me and Me/AlN/Me, a set of equations describing boundary conditions (2) is divided into two independent parts: a set of equations for the Lamb wave modes and a set of equations for SH-modes of the elastic wave.

The computing experiment was carried out with the use of the software developed by authors.

Analysis of mass load influence on waves velocities in three-layered plates. There are several determinations of piezoelectric structure sensitivity parameter to mass loading [17; 18]. In particular, S mass sensitivity of the multilayer resonator can be defined as the displacement of the relative resonator frequency normalized to the mass density surface [18]. However the disadvantage of this approach is that at great values of frequency f the changes of phase velocity at increase in thickness of a metal layer are smoothed.

In this work the following formula was used for mass sensitivity of elastic wave determination:

S = ^- (- 1, (4) dPv v )

where A v = v - v_met - the change of an elastic wave phase velocity when metallizating with a bulk density p ; d -the total thickness of metal layers. Velocities displacement is calculated concerning the elastic wave v velocity when metallizating with infinitely thin layer which does not change mechanical boundary conditions [19].

Let us note that this condition, as the computer experiment revealed, is carried out at a layer thickness less than 1 nanometer. Also the condition (4) levels the influence of the piezoelectric effect and, therefore, parameter S will not depend on the piezoelectric layer type.

The schematic representation of the studied layered structures is presented in fig. 1, а. Phase velocities dispersion dependences of the Lamb wave fundamental modes and fundamental and first modes of SH-wave on value of the hxf parameter (piezoelectric thickness x frequency) for the layered structure of Me/ZnO/Me type with orientation of the layer [100] (001) are presented in fig. 1, b, similar dependences for the layered structure Me/AlN/Me with orientation of the layer [100] (001) are presented in fig. 1, c. As a metal layer (Me) Al and Mo having various values of acoustic impedance Z = ρv were used. The acoustic impedances calculated for bulk longitudinal waves of all considered materials relate as ZAl < ZAlN < ZZnO < ZMo. The values of the material constants for aluminum and molybdenum are taken in [13], ZnO – in [20], AlN – in [21]. The change range of phase velocities of the elastic wave running modes in the structure Me/ZnO/Me at metallization with infinitely thin layers is ranging from values of a longitudinal wave phase velocity in ZnO crystal (v = 6084.14 m/s) or from zero (A0 mode) to the phase velocity of the Rayleigh wave in ZnO at the metallized surfaces ( v = 2677.6 m/s). It should be noted that due to „switching off“ of the piezoelectric effect at metallization of plate both surfaces the phase velocity of SH0 mode coincides with the velocity of a fast shear wave in ZnO crystal.

In Me/AlN/Me structure phase velocities of elastic wave running modes also change from the longitudinal wave phase velocity values in AlN film ( v = 10287.28 m/s) or from zero (mode A 0 ) to the phase velocity of the Rayleigh wave in AlN at metallized surfaces ( v = 5485 m/s). Unlike Me/ZnO/Me structure with the maximal value of the parameter h x f = 10000 m/s for calculation of Me/AlN/Me structure the range of change of the parameter h x f to 20000 m/s was increased due to the fact that phase velocities values of all elastic wave modes significantly increased.

Calculation of elastic wave phase velocities modes change was made at the ratio of a metal layer thickness to piezoelectric material thickness d / h = 0.001; 0.005; 0.01; 0.05; 0.1. Solid lines in fig. 1, b , c designated phase velocities modes of the Lamb elastic wave and SH-modes at metallization of a piezoelectric layer above and below by two infinitely metal layers which are not violating mechanical boundary conditions are shown with solid lines in fig.1, b , c . Dashed lines in fig. 1, b , c correspond to the piezoelectric material layer d / h = 0.1. In absolute values the presented values of phase velocities can be received at piezoelectric material thickness layers h = 1 mkm and each of metal layers d = 0.1 mkm at frequency change from 1 MHz to 10 GHz (20 GHz for AlN).

Metal use in a multilayer plate can considerably affect wave elastic energy redistribution due to acoustic properties of layers and also an interference between elastic wave modes falling and reflected from borders of layers. For example, in Al/AlN/Al structure at values h x f increase and metal layers of maximal thickness ( d / h = 0.1) use phase velocities of elastic wave modes tend to the value of phase velocity of the bulk shear wave in aluminum (fig. 1, c ). The similar situation occurs also when used other metals in multilayer structure. At the same time it is noted that in Me/AlN/Me structure elastic wave modes velocities at identical type of metal and the parameter value h x f decrease more significantly than in Me/ZnO/Me structure.

When comparing identical structures with metal layers different thickness it was revealed that the increase in metal layer thickness, as a rule, reduces the velocities of propagation of the first and the higher orders acoustic waves.

In fig. 2 the graph of sensitivity S calculated by formula (4) for fundamental A ₀, S ₀ modes, the first modes A 1 , S 1 of the Lamb wave and also fundamental and the two first modes of SH-wave depending on the parameter h x f in Al/ZnO/Al structure providing d / h = 0.001 is presented.

It is possible to note that on modes dispersion dependences S ₀, A ₁, S ₁ of the Lamb wave the expressed S maxima are observed. The maximal value of S = 251 sq.m/kg for S 0 mode at h x f = 2500 m/s , for A 1 mode S = 248 sq.m/kg at h x f = 4700 m/s, for S 1 mode S = 249 sq.m/kg at h x f = 7000 m / s (fig. 2).

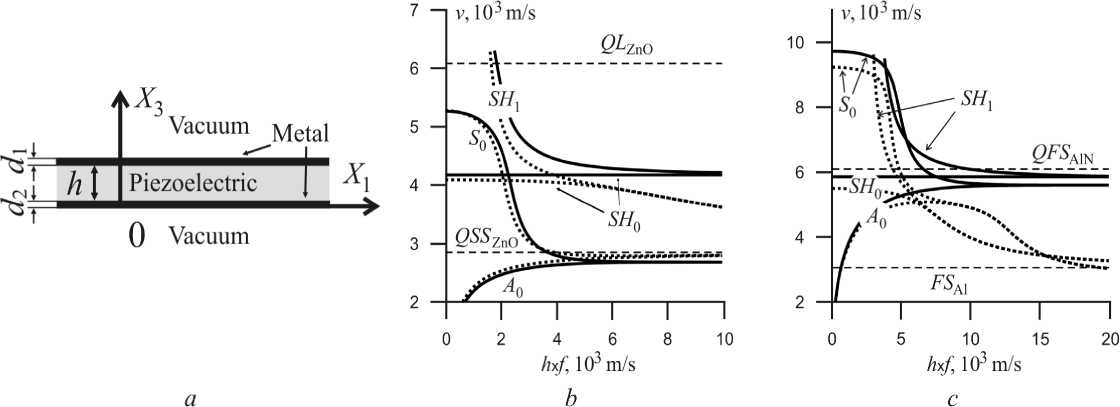
Fig. 1. Dispersive dependence of phase velocities on the product h x f for the layered structure Al/Piezoelectric/Al:

a – the scheme of the layered structure; b – fundamental and first modes of Lamb and SH -wave in the structure Al/ZnO/Al; c – fundamental and first modes of Lamb and SH -wave in the structure Al/AlN/Al. Solid lines – mode velocities for infinitely thin metal layers, dash lines – mode velocities for metal layers thickness d / h = 0.1

Рис. 1. Дисперсионные зависимости фазовых скоростей от произведения h x f для слоистой структуры Al/пьезоэлектрик/Al: а – схема слоистой структуры; б – фундаментальные и первые моды волны Лэмба и SH -волны в структуре Al/ZnO/Al; в – фундаментальные и первые моды волны Лэмба и SH -волны в структуре Al/AlN/Al; сплошные линии – скорости мод при бесконечно тонких слоях металла, точечные линии – скорости при относительной толщине металла и слоя d / h = 0,1

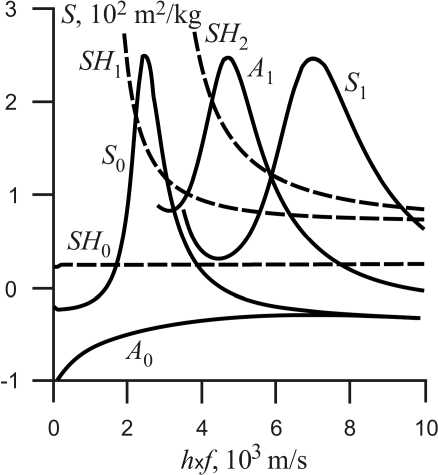
Fig. 2. Dispersive dependence of the sensitivity S for Lamb and SH -modes of an elastic wave on the product h x f for the layered structure Al/ZnO/Al. Ratio of the metal layers and piezoelectric d / h = 0.001

Рис. 2. Дисперсионные зависимости чувствительности S мод упругой волны Лэмба и SH -волны от произведения h x f для слоистой структуры Al/ZnO/Al при отношении толщин металла и пьезоэлектрика d / h = 0,001

Therefore, at metallization of a plate from above and from below by two metal thin layers the modes of an elastic Lamb wave above the zero order (except for mode A ₀) have the sensitivity maxima occurring practically through identical intervals of the parameter h x f values.

S value maxima are revealed only for the Lamb wave modes A ₁ and S ₁. They are explained by the condition of „resonance“ reflection of these waves from a piezoelectric boundary with metal layers realization, what leads to the emergence of local maxima in values of S (fig. 2). The graphs of sensitivity S fundamental mode of an antisymmetric wave A 0 and SH-mode with shear-horizontal and horizontal polarization on the studied frequency range have no peculiarities. Only the apparent dependence of the module S decrease at the increase of the parameter h x f is characteristic for them. It is possible to note that the decrease (on module) of S values is connected with gradual mode А ₀ velocity increase at the values of the parameter h x f increase. At the same time the velocity of this mode remains the minimal of all considered elastic wave modes velocities. The decrease in S values for transversal and horizontal polarization modes is connected with the same gradual decrease of these modes velocities at the increase of the parameter h x f values. Further in this work only features of acting of S sensitivity curves for the Lamb elastic wave mode having maxima on the considered range of the parameter h x f values are being described.

In fig. 3 the graphs of S sensitivity of S ₀ fundamental mode and the first modes A 1 и S 1 of the Lamb wave depending on the metal layer material, the ratio of d/h and h x f parameter in Me/ZnO/Me structure are presented. The maximal values of S parameter for S 0 mode are reached at h x f = 2400-2500 m / s and the ratio of d/h = 0.001 where condition h = 2λ/3 is satisfied, i. e. a piezoelectric layer thickness is equal to two thirds of the elastic wave S 0 length (fig. 3, а , d ). When using Al and Mo layers the value of parameter S = 251 sq.m/kg and S = 246 sq.m/kg, respectively. Essential decrease of S sensitivity for the considered elastic wave modes is particularly evident at d/h > 0.05. This decrease of S values at d/h increase is especially observed when using Mo – the metal with high acoustic impedance value. Numerical values of S maxima for both types of metal differ only at the considerable thicknesses of layers, for example, in Al/ZnO/Al structure at d/h = 0.1 the value of sensitivity of S = 200 sq.m/kg at h x f = 2300 m / s, and in Mo/ZnO/Mo structure S = 155 sq.m/kg at h x f = 2100 m / s (tab. 1). The maximal values of S parameter for A ₁ mode of the Lamb elastic wave are reached at h x f = 4700 m / s and d/h = 0.001 where the condition h = λ is satisfied, i. e. thickness of a piezoelectric layer is equal to A 1 elastic wave length (fig. 3, b, e ). The maximal values of S parameter for S 1 mode of the Lamb elastic wave are reached at h x f = 7000 m / s and d/h = 0,001 where the condition h = 3λ/2 is satisfied, i. e. the piezoelectric layer thickness is equal to one and a half length of S 1 elastic wave (fig. 3, c , f ). At the same time it was also revealed that application of Mo layers leads to more considerable decrease of the S maximal sensitivity value than when using Al.

According to the graphs in fig. 3 and to the data in tab. 1 it is noted that the increase in a metal layer thickness ( d / h ) always leads to wave frequency displacement in the S maximum to more low-frequency area.

In fig. 4 the graphs of S sensitivity of the Lamb wave fundamental and first modes depending on the metal layer type, the ratio of d/h and the h x f parameter in Me/AlN/Me structure are shown.

The maximal values of S parameter for S ₀ mode are reached at h x f = 5200 m / s and d/h = 0.001 on the condition when h = 2λ/3, as well as in the previous structure for the similar mode (fig. 4, а , d ). When using Al and Mo layers at S = 502 sq.m/kg and S = 493 sq.m/kg, respectively. Essential decrease of S sensitivity for the considered elastic wave modes is shown at d/h > 0.05, in particular when using Mo. S maxima numerical values for both types of metal differ only at the considerable thicknesses of layers, for example, in Al/AlN/Al structure at d/h = 0.1 the sensitivity value of S = 432 sq.m/kg at h x f = 4800 m / s, and in Mo/AlN/Mo structure S = 239 sq.m/kg at h x f = 4200 m / s (tab. 2). The maximal values of S parameter for A 1 mode of the Lamb elastic wave are reached at h x f = 9600 m / s and the ratio of d/h = 0.001 where h = λ condition is satisfied (fig. 4, b , e ). The maximal values of S parameter for A 1 mode of the Lamb elastic wave are reached at h x f = 13 800-14000 m / s and d/h = 0,001 where h = 3λ/2 condition is satisfied (fig. 4, c , f ).

The values of S parameter in maxima exceed similar values by 1.5–2 times for Me/ZnO/Me structure, at the same time the increase in thickness of a metal layer also leads to the wave frequency displacement in maxima of S parameter values.

At the same time unlike Me/ZnO/Me structure for the considered S ₀, A ₁, S ₁ modes of the Lamb elastic wave the essential increase in values of S sensitivity when using thick layers of Al is noted. In this case S at great values of the parameter h x f can be comparable or even exceed the values in the local maximum (fig. 4, a ). At the same time it is also possible, for example, for A 1 mode when the maximal value of sensitivity is noted at the moment of wave emergence, further the local minimum is observed and then S becomes almost dispersionless (fig. 4, b ).

In general the nature of parameter S changes in Me/AlN/Me structure is similar to changes of S in the three-layered plate of Me/ZnO/Me.

Features of S sensitivity curves of Lamb and SH waves in Me/ZnO/Me and Me/AlN/Me structures. For both structures the characteristic feature is that only S 0 , A 1 and S 1 modes of the Lamb elastic wave possess the localized by maxima S values. Other modes – antisymmetric fundamental A 0 with the lowest propagation velocity and the mode with shear-horizontal polarization of SH ₀, SH ₁, SH ₂ – have no apparent features of sensitivity curves on the studied frequency range.

Metal layers thicknesses increase results in the displacement of S sensitivity values maxima to the low-frequency area. At the same time S curve peaks amplitude and width with the increase in metal thickness for Me/ZnO/Me plate depend on the type of metal and the parameter h x f less than for Me/AlN/Me.

When comparing various structures of Me/Piezoelectric/Me type it is revealed that sensitivity values the Lamb elastic wave modes at d/h = 0.001; 0.005; 0.01 differ insignificantly. The essential de- crease of S sensitivity for the considered elastic wave modes at d/h > 0.05, in particular when using Mo, can limit metals layers of the considerable thickness application in sensor devices.

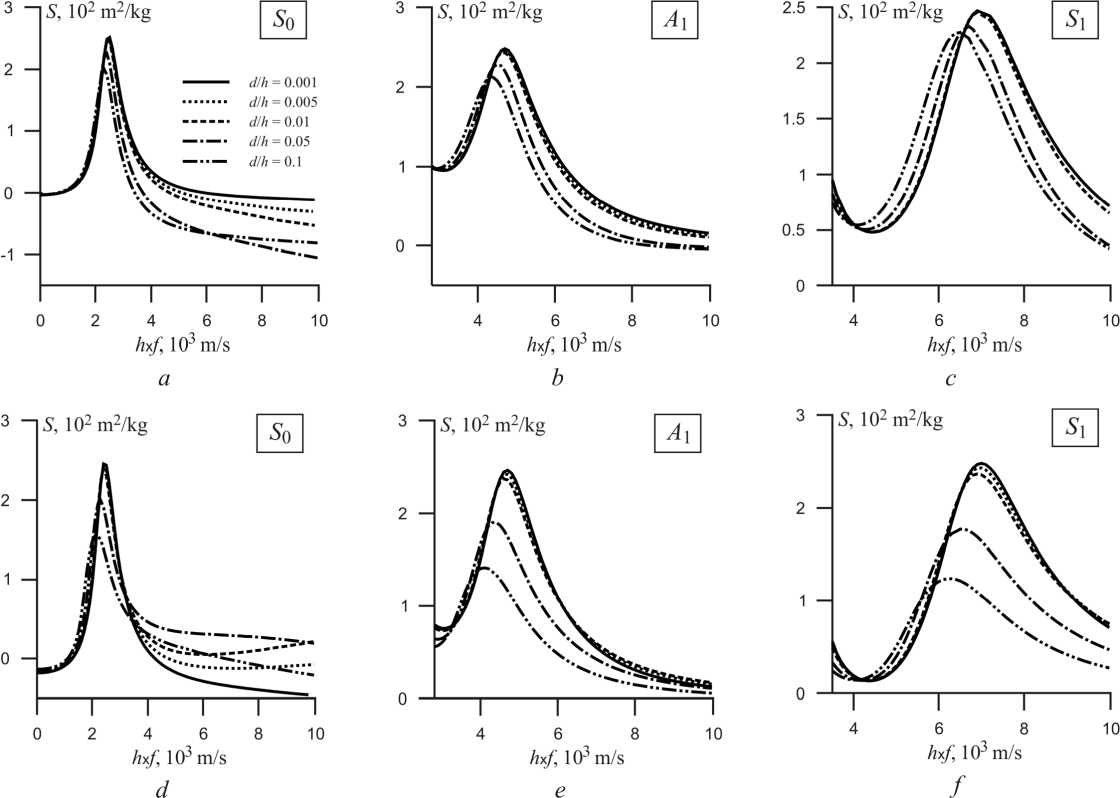
Fig. 3. Dispersive dependence of the sensitivity for 5 0 , A 1 и 5 1 modes on the product h x f for the layered structure Me/ZnO/Me: a–c – aluninium; d–f – molybdenum. Ratio of the metal layers and piezoelectric d / h : 0.001, 0.005; 0.01; 0.05; 0.1

Рис. 3. Дисперсионные зависимости чувствительности мод 50, A 1 и5 1 от произведения hxf для слоистой структуры Me/ZnO/Me:

а–в – алюминий; г–е – молибден. Отношение толщин металла и пьезоэлектрика d / h : 0,001, 0,005; 0,01; 0,05; 0,1

Тable 1

Максимальные значения чувствительности S в структуре Me/ZnO/Me

The maximum sensitivity values of S in the Me/ZnO/Me structure

d/h	Mode	S 0		A 1		S 1
	Metal	Al	Mo	Al	Mo	Al	Mo
0.001	S , m2/kg	251	246	248	247	249	248
	h x f, m/s	2500	2400	4700	4700	7000	7000
0.005	S , m2/kg	248	244	246	242	248	243
	h x f, m/s	2500	2400	4700	4700	6700	7000
0.01	S , m2kgг	246	240	244	237	245	237
	h x f, m/s	2400	2400	4700	4600	6900	6900
0.05	S , m2/kg	225	199	231	190	233	177
	h x f, m/s	2400	2300	4400	4400	6700	6500
0.1	S , m2/kg	200	155	212	141	227	124
	h x f, m/s	2300	2100	4300	4100	6500	6300
Mean value of h x f in maximum S , m/s		2420 ± 104	2320 ± 162	4560 ± 114	4500 ± 149	6760 ± 114	6740 ± 188

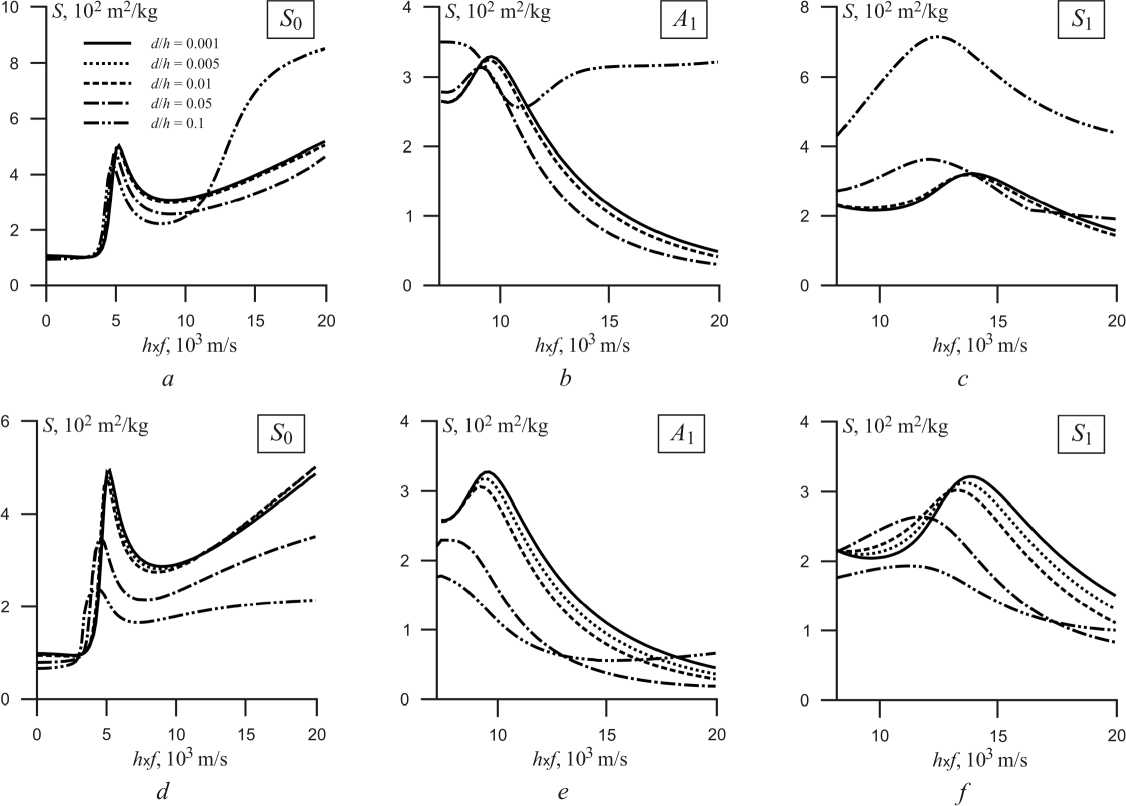
Fig. 4. Dispersive dependence of the sensitivity for 5 0 , A 1 и 5 1 modes on the product h x f for the layered structure Me/AlN/Me: a–c – aluninium; d–f – molybdenum. Ratio of the metal layers and piezoelectric d / h : 0.001, 0.005; 0.01; 0.05; 0.1

Рис. 4. Дисперсионные зависимости чувствительности мод 50, A 1 и 5 1 от произведения hxf для слоистой структуры Me/AlN/Me:

а–в – алюминий; г–е – молибден. Отношение толщин металла и пьезоэлектрика d / h : 0,001, 0,005; 0,01; 0,05; 0,1

Тable 2

Максимальные значения величины S в структуре Me/AlN/Me

The maximum sensitivity values of S in the Me/AlN/Me structure

d/h	Mode	S 0		A 1		S 1
	Metal	Al	Mo	Al	Mo	Al	Mo
0.001	S , m2/kg	502	493	329	327	323	321
	h x f m/s	5200	5200	9600	9600	14000	13800
0.005	S , m2kgг	500	489	327	318	321	312
	h x f m/s	5200	5000	9600	9400	13800	13600
0.01	S , m2kgг	497	479	324	306	319	302
	h x f m/s	5200	5000	9400	9200	13800	13400
0.05	S , m2kg	476	349	313	229	364	264
	h x f m/s	5000	4600	9000	7600	12000	11800
0.1	S , m2/kg	432	239	349	178	714	193
	h x f, msс	4800	4200	7600	7400	12400	11200
Mean value of h x f in maximum S , m/s		5080 ± 222	4800 ± 497	9040 ± 1046	8640 ± 1309	13200 ± 1153	12760 ± 1465

The feature of the elastic wave S0 mode propagation in Me/ZnO/Me layered structure is the emergence of S parameter negative values when using both Al and Mo metal layers, that is the value of the elastic wave phase velocity when metalizing, can increase (fig. 2, fig. 3, а, d).

For Me/AlN/Me layered structure this effect is not observed.

Conclusion. The influence of mass loading in the form of two metal layers (simulating the upper and lower electrode) on S sensitivity of elastic wave dispersion modes in piezoelectric layered structures Me/ZnO/Me and Me/AlN/Me change according to the frequency and d/h depends on the ratio of the metal layer acoustic impedance and acoustic line material. It is noted that the maximal values of elastic wave modes sensitivity are reached at the layered Al/AlN/Al system configuration, that is in the system with low values of acoustic impedances of a bulk longitudinal wave for layers and piezoelectric acoustic line materials. It is revealed that the maximal values of S sensitivity in all structures are observed in cases when a metal layer thickness is 2/3, 1, 3/2 of the corresponding Lamb elastic wave length. The results received during computer simulation can be useful when developing acoustic electronic devices on the Lamb waves and the SH-waves.