Синергетическая концепция при построении систем управления точностью изготовления деталей сложной геометрической формы
Автор: Заковоротный Вилор Лаврентьевич, Флек Михаил Бенсионович, Фам Динь Тунг
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Технические науки
Статья в выпуске: 10 (61) т.11, 2011 года.
Бесплатный доступ
Приводятся результаты математического моделирования, методики и построения программ ЧПУ для обработки деталей сложной геометрической формы в условиях ОАО «Роствертол».
Синергетическая концепция, качество изготовления, динамика, управление процессами обработки на станках
Короткий адрес: https://sciup.org/14249510
IDR: 14249510 | УДК: 621.9
Текст научной статьи Синергетическая концепция при построении систем управления точностью изготовления деталей сложной геометрической формы
Введение. Для авиационной промышленности характерно изготовление изделий, обладающих малой и изменяющейся жёсткостью по координатам перемещения инструмента относительно заготовки, а также деталей сложной геометрии, при обработке которых меняется направление формообразующих движений. При обработке таких деталей приходится считаться с тем, что траектории движения исполнительных элементов станка, программируемых в управляющей ЭВМ, отличаются от траекторий формообразующих движений инструмента относительно заготовки, по крайней мере, на величину упругих деформационных смещений вершины инструмента относительно точки его закрепления в исполнительном элементе. Динамические структуры металлорежущих станков вместе с процессом обработки обладают следующими свойствами [1]:
-Они являются диссипативными. Поэтому в пространстве состояния множеству UQQ соответствует множество траекторий формообразующих движений, которое является притягивающим, то есть соответствующие траектории формообразующих движений являются аттракторами.
-
- Как правило, с учётом физической реализуемости, можно выбрать такой вектор управления, формируемый в координатах исполнительных перемещений станка, которому соответствует асимптотически устойчивая траектория формообразующих движений, которая обеспечивает требуемые показатели геометрического качества обработки.
Для согласования программы ЧПУ, траекторий исполнительных элементов и траекторий формообразующих движений инструмента относительно заготовки, в случае, если обеспечиваются требуемые показатели геометрического качества изделий, возможно два подхода. Первый, широко используемый в настоящее время, основан на принципах подчинения всех координат программе ЧПУ. Второй основан на развиваемой в настоящее время синергетической теории управления и на определении UQQ таким образом, что в управлении используются естественные динамические свойства системы, в том числе и связи, формируемой процессом резания. При этом траектории формообразующих движений, обеспечивающие необходимое геометрическое качество, формируются естественным образом в данной динамической структуре и являются аттракторами системы [1, 2]. Второй подход, основанный на использовании всех дополнительных связей, рассматриваемых в парадигме расширения пространства состояния, применяемой в синергетической концепции управления, позволяет фактически включить в управление все естественно существующие связи.
Пусть определено многообразие траекторий xz е Z, обеспечивающих требуемые показатели геометрического качества обработки. Ему соответствует многообразие траекторий исполнительных элементов Хх е X, и далее программ ЧПУ Ху ell, то есть векторов управления UQQ. Если учитывать естественно существующие в динамической структуре связи и закономерности их изменения вдоль траектории движения исполнительных элементов, то именно на многообразии Ху должна строиться программа ЧПУ. Таким образом, для определения многообразия Ху необходимо решать обратные задачи динамики для уравнений, связывающих пространства X, 7и U. Алгоритм определения траекторий формообразующих движений. В статье ограничимся случаем токарной обработки. Случаи фрезерования концевыми фрезами, рассверливания, обработки отверстий многолезвийными инструментами подробно рассмотрены в монографиях [1—3]. Будем полагать заданными траектории исполнительных элементов, т. е. ^Х, (X^.dX^X^dtY
/ = 1,2,3,4. Их можно представить в функции времени, т. е. {%, (t),V( (t)], где
-
V, ^ = dXi ^Jdt . Каждой точке вектора X соответствует пара векторов упругих деформаций ин
струмента х = ^xv хг, х3} и заготовки у = {ук уг, у3} . Координаты X отсчитываются от центра вращения заготовки, находящегося на правом её конце (рис. 1). Упругие деформации х = ^xv хг, х3}, у = {ук у2, у3^ отсчитываются по направлению, противоположному телу заготовки (рис. 1). Таким образом, координаты формообразующих движений, определяющие геометрию детали, складываются из координат исполнительных элементов станка и упругих деформаций. Например, текущее значение радиуса г1^ в точке Х^, определяющее значение диаметра
D^, равно
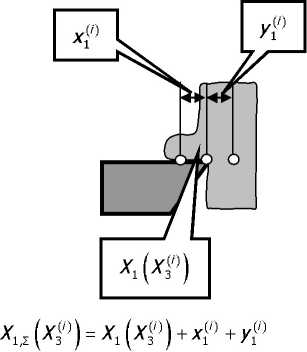
• ^Л3 ) “ Z1 кЛ3^ “ ЛЦЛ3 ^ЛЦЛ3 р/ЦЛ3 )
Тогда точка z,(X3) — координата формообразующих движений, а точка Хх(Х3) — точка координат исполнительных элементов станка. Имеет также место упругое смещение точки контакта инструмента и заготовки по отношению к координате Х^ на величину х3 (х4' ^) + Уз (^)-
Выясним закономерности формирования упругих деформаций при заданных траекториях ^Xj (t^Vj (f)}. Упругие же деформации прежде всего зависят от сил. Силы резания при обработке на металлорежущих станках формируются в результате пересечения тела режущего инструмента с заготовкой с учётом деформаций х, у (рис. 2). Уровень моделирования сил резания F =^FvF2,F3Y в координатах состояния может быть различным. Для того чтобы выяснить основные закономерности преобразования траекторий, будем анализировать медленные формообразующие движения, то есть полагать, что процесс резания по координатам упругих деформаций инструмента относительно заготовки является устойчивым и в пределах импульсной реакции подсистемы инструмента и заготовки система является замороженной. Более точные обоснования иерархии систем дифференциальных уравнений динамики даны в монографии [1].
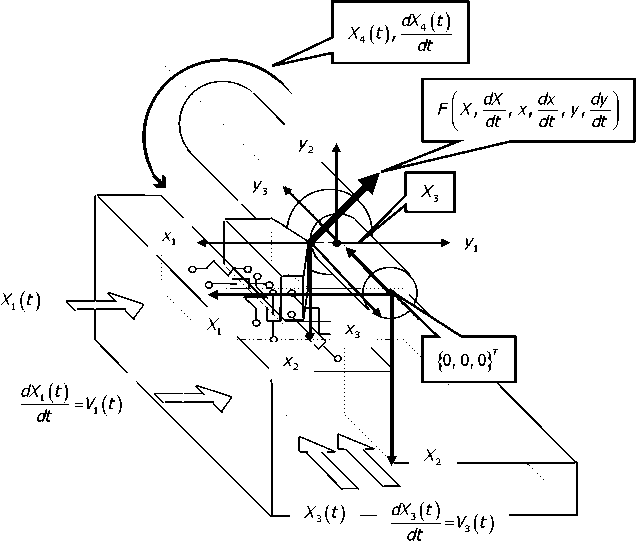
Рис. 1. Система координат, определяющая состояние управляемой динамической системы точения без учёта электромеханического преобразователя
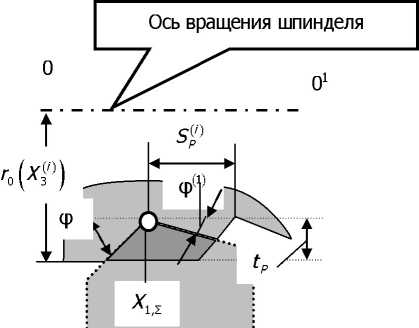
Рис. 2. Схема формирования площади срезаемого слоя и координаты формообразующих движений по направлению Ai с учётом упругих деформаций
Тогда при формировании сил резания F = ^FvF,,F3y можно принять следующие гипотезы (рис. 2) [1]:
— модуль сил пропорционален площади срезаемого слоя S, т. е.
/=Ъ=Р(Ит)^; (2)
— справедлива гипотеза неизменной ориентации сил в пространстве, т. е.
F=^,F.,F3 f =F^xY,x2,x3y, (3)
где Л ={ЛР Л2, Л3}г — вектор угловых коэффициентов. Заметим, что коэффициент р, имеющий смысл давления на переднюю поверхность инструмента, также зависит от износа инструмента.
Таким образом, силы при неизменных условиях определяются величиной подачи на оборот Sp^t) и глубиной резания tP(t) (рис. 2)
5(f) = 5,(f)f,(f)-C5)(f),
7 1 tgcptgcp(1) _ /,х г ~ ~ „ где ч t ; Sp\t)= | [И3(^)-иХз\t)-vy3 — пройденный вершиной инст румента за время одного оборота Т с учётом скорости упругих деформаций в направлении
Заметим, что в (4) предполагается движение инструмента вдоль обрабатываемой детали. При его движении по направлению оси вращения заготовки необходимо учитывать срезание материала на предыдущем обороте. Тогда на временном отрезке движений инструмента в сторону оси вращения детали величина глубины резания фактически определяется величиной подачи, то есть определяется по зависимости Sp(t^ = [ [l/^t)-^ (t)-yy3 (t)]tft. При движении инстру- мента вдоль оси вращения заготовки (это наиболее типичный случай для токарной обработки) силы, формируемые процессом резания, определяются следующими интегральными преобразованиями:
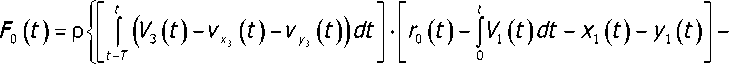
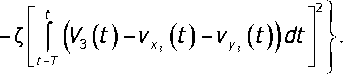
Причём знак скорости упругих деформаций и , и зависит от знака dF0/dt . Заметим,
t что r0^X3)-^(t^dt-x^f)-y^t^O, в противном случае контакт инструмента с заготовкой О отсутствует и процесса резания нет.
Введём в рассмотрение матрицы жёсткости подсистемы инструмента с(х)(Х3) = ^с£Ла] , s, А-=1,2,3 и заготовки с(к) =[с$Лк], s, к = 1,2,3. Во многих случаях бывает справедливым с(х) (Х3) = const. Пренебрегая в (5) квадратичными формами относительно малых упругих деформаций, а также учитывая, что С есть величина малая, получаем линеаризованное выражение для определения связи траекторий исполнительных элементов с траекториями упругих деформаций инструмента относительно заготовки:
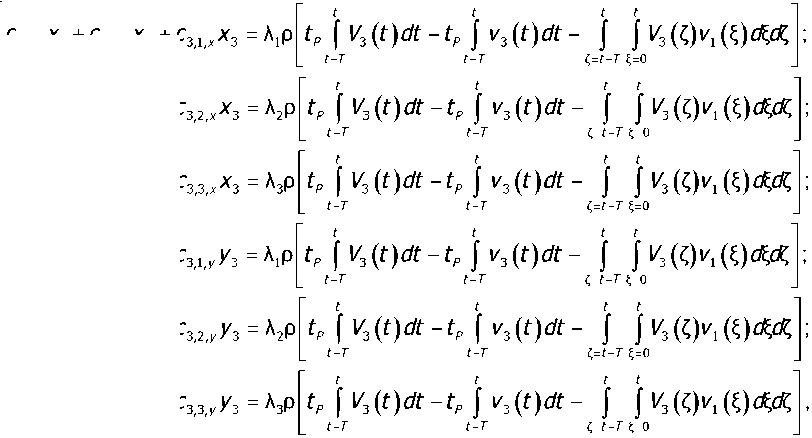
^——. В (6) полагается, что величина припуска tp = const.
где v.
|
Р\Д,хХ\ |
+ Рд,хХ7 |
+ С- |
|
Cv,7,xXY |
+ ^1Д,хХ1 |
+ С- |
|
Р\,3,хХ\ |
Рд,/Х7 |
+ с |
|
Рд.уУ, |
+ ^2,1, уУ 7 |
+ С- |
|
Рд^У, |
+ ^2,2, уУ 7 |
+ С- |
|
Рд.уУг |
+ ^2,3, уУ 7 |
+ С- |
|
_d(yx |
+ %1) |
с |
В частности, если скорость 1/3 можно считать постоянной (усреднённой) в пределах оборо- где
= const, то для вычисления упру-
|
C^x^'^ = F, |
|
|
Рд.х + ^1Р5р ^2,1,% |
СЗДх + ^ptp PpSp 0 ^iPtp |
|
1,2,х 2,2,х |
^3 7 x +^7Ptp K.pSp 0 k^Ptp |
|
с. о + Лор5р сэ о 1,3, х v2,3,x |
^3,3, x "*" ^зР^Р K3pSp 0 ^3Ptp |
|
K^Sp 0 |
K^ptp С^д у + ^pSp ^2,1,у ^3,1,у "*" ^iPtp |
|
KypSp 0 |
^ptp ^1,1,у "*" ^7?Sp P7,7,y Рз,7,у "*" ^7P^P |
|
K3pSp 0 |
^зР^Р Рд, у + ^зРЗр ^7Д, у ^3,3,У + ^зР^р |
|
X^ |
'^ — f Y Y V V V " — Лг, Лз, у I, у 7, уз^ , |
та заготовки и величину припуска в пределах оборота также tp гих деформаций хи у на каждом обороте из (6) получаем
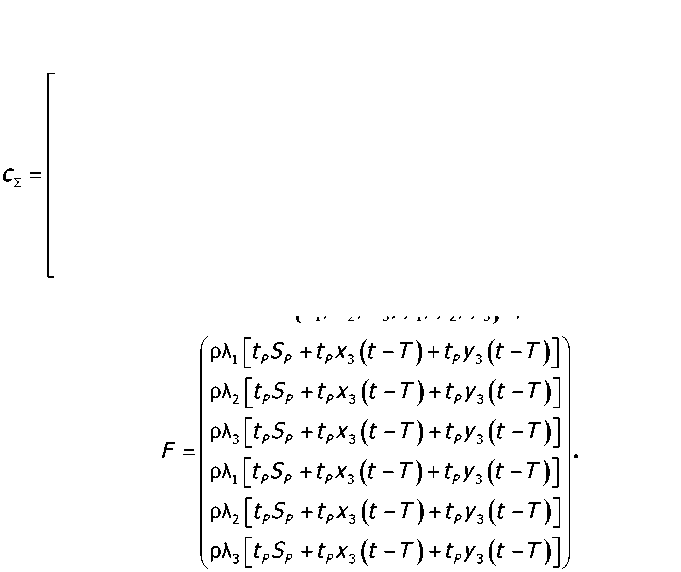
Вектор F кроме технологических режимов включает заданные функции х^-Г) И у, (t -Т) , которые определяются на отрезке (0, t-T) при определении деформаций в момент t Если вычисление деформаций осуществляется в пространстве состояния по координате Хз от оборота заготовки к обороту, то x^t-T) и у^-Т^ равны значениям упругих деформаций на предыдущем обороте. Таким образом, суммарная матрица жёсткости, имеющая размерность
6x6, складывается из матриц жёсткости инструмента, заготовки и коэффициентов, зависящих от технологических параметров, а также параметров процесса резания (определяются обобщённым коэффициентом р).
Кроме этого, будем считать направляющие станка идеальными, т. е. не вносящими искажений в траектории формообразующих движений. Принципиально кинематические возмущения со стороны направляющих можно учесть, если задана их статистика. Тогда для обеспечения, например, неизменности диаметра необходимо выполнить условие
%i - (%! + yj = const,
которое можно выполнить на основе решения обратной задачи динамики из (7) различным подбором Хх (Х3) и Sp (Х3). Условие (8) фактически определяет один из инвариантов функционирования станка в синергетической теории управления [4]. Кроме этого, tp и 5Р в (7) есть параметры управления. Подчеркнём, что траектории исполнительных элементов через изменения параметров управления смещают траекторию формообразующих движений. В общем случае перестраивают динамическую систему резания.
Связанная между собой совокупность Хх^Х3^, 5Р(Х3^, изменяющаяся по координатам перемещения суппорта вдоль оси вращения заготовки, после элементарных преобразований даёт совокупность траекторий исполнительных элементов, обеспечивающих требуемое в данном случае условие (8). Эти траектории и формируют многообразие е X траекторий исполнительных элементов станка, обеспечивающее условие (8), т. е. неизменность диаметра — одна из целей процесса резания.
Приведённые условия легко обобщаются на случай, когда деталь имеет сложную геометрическую форму. Здесь ограничимся случаем, когда геометрия детали допускает кусочнолинейную аппроксимацию (линейная интерполяция) и выделим на детали отдельный фрагмент (рис. 3). На этом фрагменте обработка ведётся с одновременным изменением скоростей продольной и поперечной подачи (в данном случае обрабатывается элементарный конус). При анализе траекторий в пределах /-го оборота частоту ш4 будем считать неизменной, т. е. 7м = 1/ш^ . Если заданы скорости Ух (t), 1/3 (t) и их вектор ориентирован по направлению образующей, то величина подачи на Ам обороте будет равна
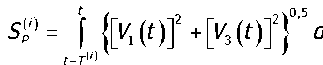
Причём при линейной интерполяции для обеспечения движений по образующей М -N (рис. 3) должно выполняться требование 1/3 ^(Vx (t) = k^’^ = const, если упругие деформации отсутствуют, то многообразие траекторий частот вращения двигателей исполнительных элементов станка (ш. (ХАш, , обеспечивающих движение по желаемой образующей
«М -N », определяется соотношениями:
v v 7 (10)
где Vp — скорость резания, (л^, ш3 — частоты вращения двигателей поперечной и продольной подач
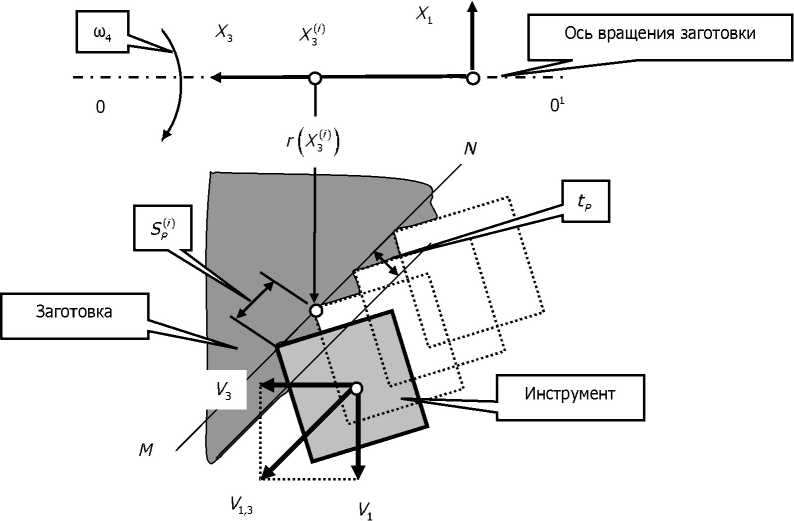
Рис. 3. Схема формирования формообразующих движений при точении детали сложной геометрической формы
Если Vp постоянна и соответствует традиционно определяемой оптимальной скорости резания, то частота вращения шпинделя есть функция радиуса, т. е. координаты Х3 ; коэффициент ki-M,N'1 определяется углом наклона образующей М -N (см. рис. 3). Упругие деформации инструмента в направлениях Хх и Х3 искажают реальную образующую (рис. 4). Если упругие деформации отсутствуют, то в процессе управления приводами за счёт асимметрии динамических характеристик приводов может нарушаться одно из условий (10), что не только вызывает отклонение реальной траектории относительно образующей М - /V, но и приводит к дополнительным возмущениям.
Для выяснения механизмов отклонения траекторий введём в рассмотрение вектор скоростей VlMN) =^MN1(X3),V^MN1(X3)^, отличающийся от V = {Ц (Х3 ), 1/3 (Х3 )[г матрицей перехода, зависящей от угла q>w , определяемого углом между осью вращения заготовки О,О1 и образующей MN (рис. 4). Связь между скоростями определяется геометрическими соотношениями
И*)(%3) = Ф1/(%3),
(И)
где ср =
5Юфж
— COS фдда
COS ф/ад ^ПфМЛ
Если 1/3 (%3)з1пфж = Ц(%3)cosфж, то суппорт движется по прямой М -N . Тогда формирование сил резания соответствует ранее проанализированному случаю, но вместо скорости 14 (%3) необходимо рассматривать скорость l/3(W) = 1^ (X3)sinQw + I/3(%3)cosqm/v и учитывать изменение угловых коэффициентов ориентации сил резания. Очевидно, что условию 14 (Х3) sin ф^ = Ц (Л^соэф^ соответствует выполнение второго соотношения в (10). Тогда для вычисления упругих деформаций для подсистемы инструмента (обрабатывается жёсткая деталь) можно воспользоваться соотношениями
|
с№х№ = р, |
(12) |
|
|
Сц COS фд^у ^зд ^in Фм/v ^д ^1д51Пфд^ + С3дСО5фж |
||
|
где cw = |
С1д cos ф^ — с3д sin фд^у С2д С^2 ^^ Фж "*~ С*з,2 COS Фд^/у |
, причём коэффициенты с5Л , |
|
С^з COS ф^ — C^ Sin ф^ С2,3 С^з Sin фд^ + С33 COS фж |
-
s, к =1,2,3 есть элементы матрицы жёсткости в системе координат х, т. е. при cpM/v=O cw = с . Для определения вектора управления (программы ЧПУ) полученное многообразие траекторий к\ необходимо перевести в многообразие ку. Эта операция осуществляется на основе прямой подстановки траекторий ^Х ^.dX^/dt] е N\ в уравнения управляемых двигателей исполнительных элементов. Тем самым учитывается не только особенность преобразования траекторий исполнительных элементов в траектории формообразующих движений, но и динамические особенности приводов, в частности, асимметрия их динамических характеристик.
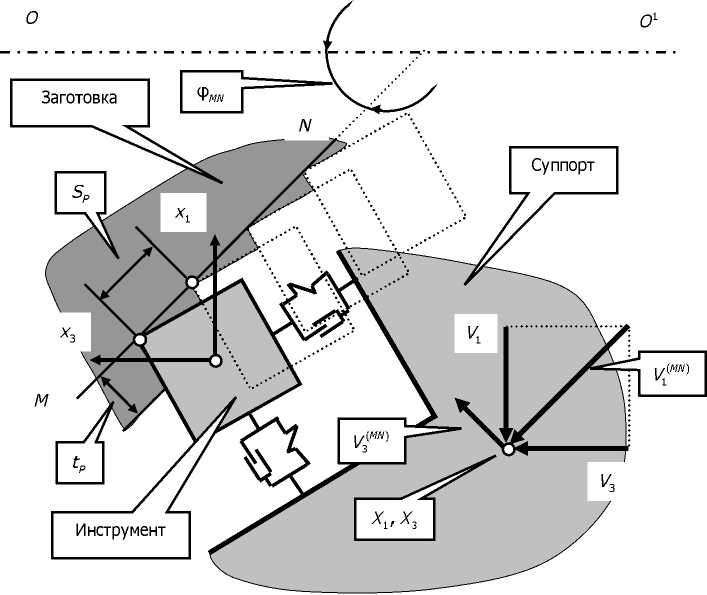
Рис. 4. Связь площади срезаемого слоя с траекториями Vt (%3), 1/3 (Х3) и упругими деформациями х3 (%3), х, (Х3)
Пример использования синергетической концепции. Рассмотрим модельный пример, соответствующий точению вала диаметром d =20,0 мм и длиной £ = 430 мм из Ст45. На рис. 5 приведена расчётная схема, а на рис. 6 — диаграммы изменения элементов матрицы жёсткости подсистемы заготовки, рассчитанные по методу конечных элементов. Матрицы жёсткости рассчитаны на основе программного комплекса ИСПА-386 — интегрированной системы прочностного расчёта методом конечных элементов. Для рассматриваемого модельного примера параметры матрицы жёсткости точек крепления заготовки и подвески режущего инструмента приведены в табл. 1. Для расчёта смещения точки равновесия xx+yx=w, усреднённой по периодам вращения заго- товки, и определения траектории «медленного» изменения скорости подачи {Х3 (т),^/^} е X необходимо иметь значения параметра р, которые приведены в табл. 2 для случая обработки Ст45 трёхгранными неперетачиваемыми пластинами из твёрдого сплава Т15К6 при варьировании скорости резания в диапазоне Vp = (60,0 4-180,0) м/мин для величины припуска tp = 2,0 мм.
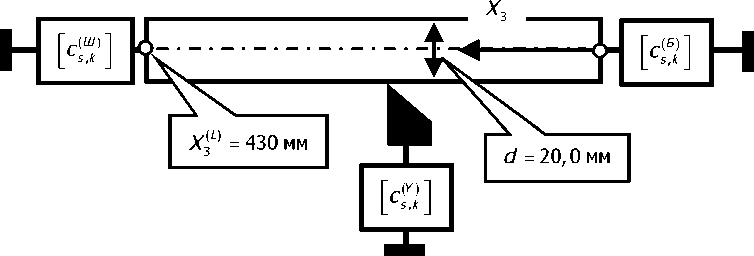
Рис. 5. Расчётная схема для определения матриц жёсткости заготовки по длине контакта инструмента и детали
Таблица 1
Исходные матрицы жёсткости системы резания
|
Наименование |
cu, кГ/мм |
С2,2' кГ/мм |
С33' кГ/мм |
С2Д' кГ/мм |
С3д, кГ/мм |
С3,2' кГ/мм |
|
Матрица жёсткости крепления заготовки в патроне [с^] |
8,0-104 |
6,8-104 |
5,8-104 |
4,2-103 |
2,8-103 |
2,4-103 |
|
Матрица жёсткости крепления заготовки в задней бабке ГС<6И |
1,3. ю4 |
0,8-104 |
7,2-104 |
0,5-103 |
2,8-103 |
2,3-103 |
|
Матрица жёсткости подсисте- Г (к) 1 мы инструмента сц |
0,5-104 |
0,3-104 |
0,3-104 |
0,08-Ю4 |
0,05-Ю4 |
0,04-Ю4 |
Таблица 2
Изменение коэффициента р при варьировании скорости резания
|
Vp, м/мин |
р, кГ/мм2 |
|
60,0 |
290,0 |
|
100,0 |
250,0 |
|
140,0 |
220,0 |
|
180,0 |
210,0 |
На рис. 7 приведены рассчитанные траектории изменения скорости подачи при различных значениях скорости резания Vp, при которых выполняется условие и/= const. Во всех случаях величина припуска считается постоянной равной tp =2,0мм. На рисунке вместо скорости приведена частота вращения шпинделя, которая, что очевидно, при неизменном диаметре детали отличается от скорости на коэффициент.
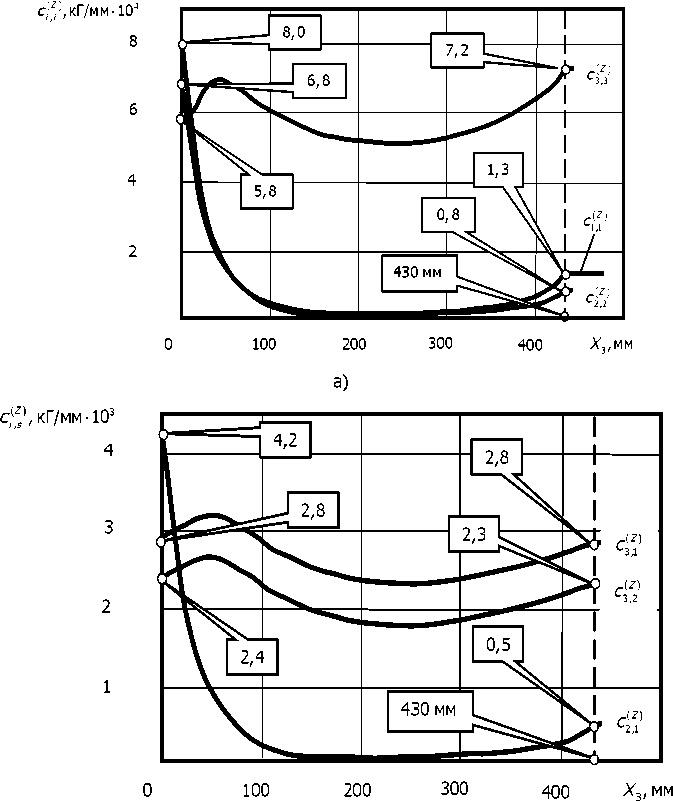
б)
Рис. 6. Изменение матриц жёсткости заготовки вдоль координат обработки а — диагональные элементы; б — недиагональные элементы
Все траектории, принадлежащие поверхности, приведённой на рис. 7, и удовлетворяющие условию dXjdt>0, обеспечивают обработку с постоянными значениями упругих деформаций инструмента относительно заготовки в направлении, нормальном к оси вращения шпинделя. На приведённой иллюстрации траектория А соответствует обработке при неизменной частоте вращения шпинделя, а траектория В — при монотонно возрастающей. Направление движения суппорта показано стрелками. На участке 1—2 скорость остаётся неизменной, она соответствует скорости врезания инструмента в заготовку. Кроме этого, по расчётам на участке врезания наблюдается резкое возрастание скорости подачи, которое на иллюстрации не показано. Оно длится в течение 2—3 оборотов и связано с переходными процессами в зоне резания. Сразу обратим внимание на многовариантность таких траекторий.
Естественно поставить вопрос о выборе на многообразии некоторой единственной траектории, являющейся оптимальной в определенном смысле. Методика выбора траектории оптимальной скорости резания вдоль траектории движения инструмента относительно заготовки по критерию минимизации приведённых затрат на изготовление партии изделий изложена в работах [5, 6]. Здесь же подчеркнём, что речь идёт не об оптимальной, но неизменной скорости резания, традиционно рассматриваемой в технологических исследованиях, а об оптимальной траектории. Такая траектория вычисляется на основе решения неклассических вариационных задач, в данном случае — на основе принципа динамического программирования.
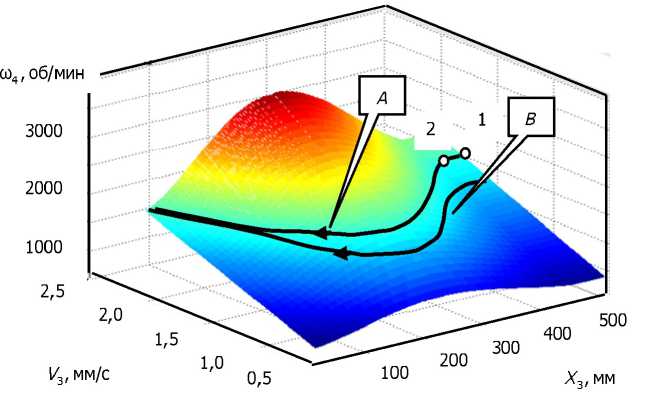
Рис. 7. Многообразие траекторий исполнительных элементов станка, обеспечивающее постоянство упругой деформации инструмента относительно заготовки при изменениях скорости подачи и частоты вращения шпинделя
Заключение. Опыт использования синергетической концепции при обработке изделий в условиях ОАО «Роствертол» показал возможность снижения трудоёмкости изготовления изделий ответственного назначения на 30-40 %. Однако внедрение этого метода в полной мере требует модернизации существующих на предприятии систем ЧПУ. Сущность модернизации заключается в установке сопроцессоров непрерывного управления траекториями исполнительных элементов, позволяющих обеспечивать изменение в каждом кадре управления скоростью по перемещению. При построении программы ЧПУ используется линейная интерполяция, но она осуществляется не по геометрическому образу детали, а по многообразию ку . При этом используются связи, естественно существующие в динамической системе станка и формируемые в процессе резания, которые автоматически обеспечивают принцип когерентности при управлении. Изложенный подход можно распространить на обработку концевыми фрезами, а также на другие процессы обработки, в том числе многолезвийными инструментами [1]. Этот подход, дополненный сопроцессорами динамического мониторинга обработки [7—9], характеризует новый этап в создании систем управления станками в интегрированном производстве.
Список литературы Синергетическая концепция при построении систем управления точностью изготовления деталей сложной геометрической формы
- Заковоротный, В. Л. Динамика процесса резания. Синергетический подход/В. Л. Заковоротный, М. Б. Флек. -Ростов-на-Дону: Терра, 2006. -876 с.
- Флек, М. Б. Технологичность и технология механической обработки деталей вертолётов/М. Б. Флек. -Ростов-на-Дону: Терра, 2004. -224 с.
- Флек, М. Б. Управление формообразующими траекториями на станках с ЧПУ. Тенденции и подходы/М. Б. Флек. -Ростов-на-Дону: Изд-во ИУИ АП, 2001. -116 с.
- Синергетика и проблемы теории управления/под ред. А. А. Колесникова. -Москва: Физматлит, 2004. -504 с.
- Определение оптимальных траекторий формообразующих движений при обработке резанием/В. Л. Заковоротный [и др.]//Вестник Донского гос. техн. ун-та. -2001. -Т. 1. -№ 3 (9). -С. 86-107.
- Заковоротный, В. Л. Методика выбора оптимальных траекторий формообразующих движений при обработке резанием/В. Л. Заковоротный, Д. А. Волошин//Исследования станков и инструментов для обработки сложных поверхностей. -Саратов: Изд. центр Саратовск. гос. техн. ун-та, 2002. -С. 35-47.
- Заковоротный, В. Л. Построение информационной модели динамической системы металлорежущего станка для диагностики процесса обработки/В. Л. Заковоротный, И. В. Ладник//Проблемы машиностроения и надёжности машин. -1991. -№ 4. -С. 75-79.
- Заковоротный, В. Л. Информационное обеспечение системы динамической диагностики износа режущего инструмента на примере токарной обработки/В. Л. Заковоротный, Е. В. Бордачёв//Проблемы машиностроения и надёжности машин. -1995. -№ 3. -С. 95-103.
- Заковоротный, В. Л. Динамический мониторинг состояния процесса резания/В. Л. Заковоротный, Е. В. Бордачёв, М. И. Алексейчик//СТИН. -1998. -№ 12. -С. 6-13.


