Синергетические базы знаний

Актуальным направлением развития интеллектуальных систем (ИС) является совместное использование методов и средств различных способов представления знаний. В настоящее время широко развиты работы по созданию гибридных систем [1-2]. Гибридизация представляет собой такое объединение методов и технологий, когда различные блоки системы реализуют какой-либо метод решения задач и взаимодействуют между собой. Гибридизация охватывает методы, объединяемые термином «мягкие вычисления» ( softcomputing ), которые включают: нечёткие системы [3, 4], нейронные сети [4-8], генетические алгоритмы [4, 9], и др. [10]. Представляется целесообразным расширить круг объединяемых методов, в который включить методы чётких вычислений «классического» искусственного интеллекта (ИИ) [11].

Синергетические системы ИИ обладают такими основными характеристиками, как множеством неоднородных компонентов и гибких взаимосвязей между компонентами, активностью, автономностью, семиотической природой взаимосвязей, открытостью, высоким эволюционным потенциалом. Архитектура и технологии синергетического ИИ отличаются неоднородностью, гибридностью, объединением различных информационных технологий [12].

1    Словарь базы знаний

Для создания синергетической системы ИИ необходимо рассмотреть возможность гибридизации передовых методов теории программирования и классического ИИ [13]. Ядром для построения синергетической системы ИИ являются чёткие знания классического ИИ. Нечёткие знания строятся на базе лингвистических переменных. Для наполнения математи- ческих знаний семантикой над ними нужно надстроить систему чётких знаний. При этом формальные математические переменные, связанные с переменными словаря базы знаний (БЗ), получают смысловое содержание.

Фундаментом для построения чётких знаний является словарь. Словарь имеет имя и методы, обеспечивающие сортировку и поиск слов, а также импорт слов из текстовых документов. Словарь состоит из слов, каждое из которых обладает именем-идентификатором, общепринятым наименованием и типом (целый, действительный или символьный). Имеются методы добавления и удаления слов, а также определения входимости слов в модули знаний (МЗ). Со словами могут быть связаны ассоциативные списки допустимых значений. Ассоциативные списки, также как и слова, имеют имя-идентификатор, наименование списка и тип значений. С ассоциативными списками связаны методы добавления, удаления, сортировки и поиска списка. Списки состоят из элементов, каждый из которых должен иметь значение и может быть добавлен или удалён.

На рисунке 1 приведён пример фрагмента словаря и ассоциативных списков для построения нечёткой БЗ. На основе словаря строятся МЗ [14]. Каждый МЗ имеет наименование, имя-идентификатор, имя предусловия и версию. С модулем связаны методы добавления, выбора модуля-аналога, трансляции и тестирования модуля, определения входимости МЗ в БЗ и другие модули, а также удаления модуля. МЗ имеет свой словарь, представляющий собой подмножество терминов из словаря БЗ и включающий входные и выходные переменные. Предусловие определяет область определения модуля и содержит набор взаимосвязанных логических выражений.

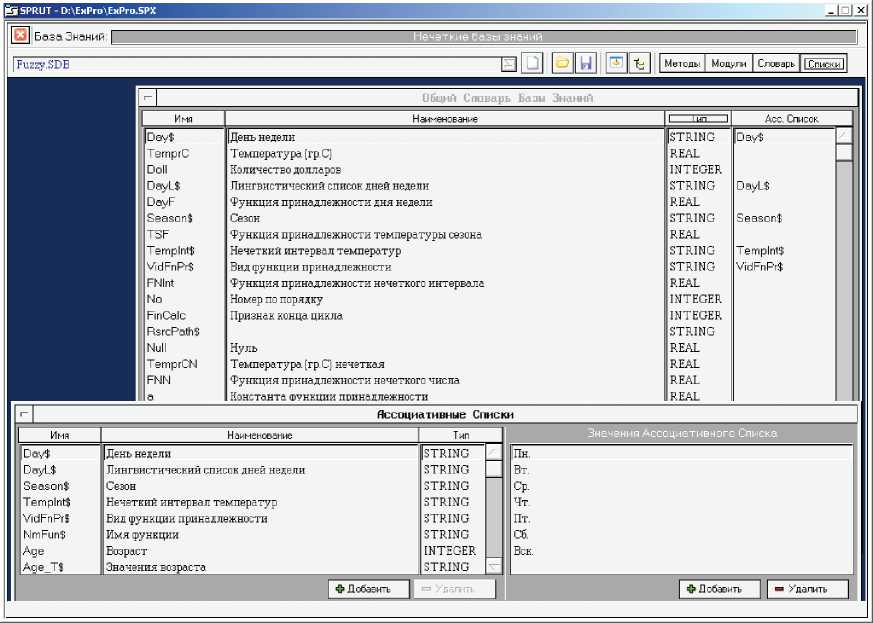
Рисунок 1 - Пример фрагмента словаря для построения нечёткой базы знаний

На рисунке 2 приведён пример модуля расчёта по формуле. Модуль имеет наименование «Расчёт функции принадлежности нечёткого числа по Гауссу» и имя «RsFNNG». Механизм модуля реализует формула FNN = 2.718^(-a_*(quant-quantn)^2).

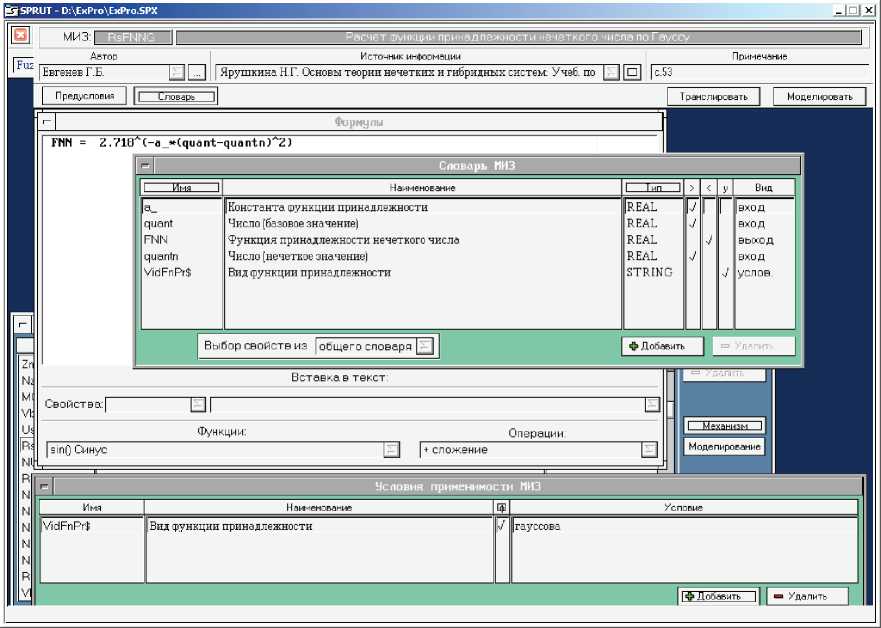
Рисунок 2 - Пример модуля знаний с механизмом вычисления по формуле

Словарь модуля включает входные переменные: a - константа функции принадлежности, quant - число (базовое значение), quantn - число (нечёткое значение), а также выходную переменную FNN - функция принадлежности нечёткого числа и управляющую переменную VidFnPr $ - вид функции принадлежности. Модуль применяется, если вид функции принадлежности имеет значение «функция Гаусса» [14].

2    Лингвистические переменные

Системы нечётких продукций строятся на основе понятия «лингвистическая переменная» [15]. Лингвистической переменной называется пятерка { x,T(x), X,G, M }, где x - имя переменной; T(x) - множество имён лингвистических значений переменной x , каждое из которых является нечётким множеством на множестве X ; G - синтаксическое правило для образования имён значений x ; M - семантическое правило для ассоциирования каждой величины значения с её понятием.

Например, лингвистическую переменную «возраст человека», можно представить так: х:     «возраст»;

X:    множество целых чисел из интервала [1, 120];

T(X): значения «молодой», «зрелый», «старый»;

• G:    «очень», «не очень» - модификатор возраста (например, «очень молодой», «не очень

старый» и пр.);

M:   правило, определяющее вид функции принадлежности для каждого значения из мно жества T.

В структуре чётких знаний лингвистическая переменная представляется в виде структурированного МЗ (см., например, таблицу 1).

Таблица 1 – Пример МЗ лингвистической переменной «возраст человека»

имя	наименование	тип	вид
x —	Переменная x	REAL	вход
Age_G$	Модификаторы возраста	STRING	выход
Age_T$	Значения возраста	STRING	выход
FnPr	Функция принадлежности	REAL	выход
a —	Константа функции принадлежности	REAL	локал.
dax	Разность а - х	REAL	локал.
dxb	Разность х - в	REAL	локал.
b_	Константа 2 функции принадлежности	REAL	локал.

В описываемом модуле использована шкала возрастов. Функция принадлежности равна 1: для значения «молодой» – до 30 лет, для значения «зрелый» – от 30 до 60 лет, для значения «старый» – от 60 лет. Модификатор возраста действует при отклонениях от этих значений в пределах 5 лет (например, до 35 лет – не очень молодой).

Например, для значения возраста «молодой» используется функция принадлежности класса L , которая определяется как:

Г 1, т ^ а,

Ь(^«,6) = < Й> а ^я О,

.

Структуры МЗ для расчёта этой функции имеют следующий вид.

МЗ: MRsFPrL - Метод расчёта функции принадлежности класса L

Предусловия запуска имя наименование тип условие

Age _ T$ Значения возраста STRING молодой

Входные свойства имя наименование тип значение x_ Переменная x                    REAL a_ Константа функции принадлежности REAL b_ Константа 2 функции принадлежности REAL

Механизм - Внешний Метод

Метод:    RsFPrL Расчет функции принадлежности класса L

Согласование свойств внешнего метода и свойств МЗ

a_	Константа функции принадлежности	=	a_	Константа функции принадлежности
b_	Константа 2 функции принадлежности		b_	Константа 2 функции принадлежности
x_	Переменная x	=	x_	Переменная x
FnPr	Функция принадлежности	=	FnPr	Функция принадлежности

Выходные свойства имя наименование тип значение

FnPr Функция принадлежности REAL

Используемые здесь константы в соответствии с принятой шкалой назначаются с помощью модуля.

МЗ: NzPrAge - Назначение параметров возраста

Предусловия запуска имя наименование тип условие

Механизм - Формула a_ = 30, b_ = 60

Выходные свойства имя наименование тип значение b_ Константа 2 функции принадлежности REAL a_ Константа функции принадлежности REAL

МЗ: NzAgG - Назначение модификатора возраста

Предусловия запуска имя наименование тип условие

Входные свойства

имя	наименование	тип	значение
FnPr	Функция принадлежности	REAL

Механизм - Таблица

Конф игурация свой ств в таблице

FnPr Age_G$

Таблица

1	очень
[0,1)	не очень

Выходные свойства

имя	наименование	тип	значение
Age_G$	Модификаторы возраста	STRING

3    Нечёткие базы знаний

Основой для проведения операции нечёткого логического вывода является база правил, содержащая нечёткие высказывания в форме «ЕСЛИ-ТО», и функции принадлежности для соответствующих лингвистических переменных (термов). При этом должны соблюдаться следующие условия.

• 1)    Существует хотя бы одно правило для каждого лингвистического терма выходной переменной.

• 2)    Для любого терма входной переменной имеется хотя бы одно правило, в котором этот терм используется в качестве предпосылки (левая часть правила).

В противном случае имеет место неполная база нечётких правил.

Пусть в базе правил имеется m правил вида:

R 1 : ЕСЛИ x 1 это A 11 … И … x n это A 1n , ТО y это B 1

R i : ЕСЛИ x 1 это A i1 … И … x n это A in , ТО y это B i

Rm: ЕСЛИ x1 это Ai1 … И … xn это Amn, ТО y это Bm, где xk, k=1..n – входные переменные; y – выходная переменная; Aik – заданные нечёткие множества с функциями принадлежности.

Результатом нечёткого вывода является чёткое значение переменной y^* на основе заданных чётких значений x k .

В общем случае механизм логического вывода включает четыре этапа: введение нечёткости (фазификация), нечёткий вывод, композиция и приведение к чёткости, или дефазификация. Алгоритмы нечёткого вывода различаются главным образом видом используемых правил, логических операций и разновидностью метода дефазификации.

Нечёткий вывод приведён на примере механизма Мамдани (Mamdani) [1,2]. Это наиболее распространённый способ логического вывода в нечётких системах. В нём используется ми- нимаксная композиция нечётких множеств. Данный механизм включает в себя: процедуру фазификации; нечёткий вывод; композицию, использующую максимальную композицию нечётких множеств; дефазификацию, или приведение к чёткости. Используются несколько методов дефазификации, например, метод среднего центра, или центроидный метод.

Пример применения нечёткой БЗ в задаче определения времени стирки на машине.

На входе БЗ имеются чёткие переменные: масса белья в килограммах ( Mass ) со множеством чисел из интервала от 0 до 5 и температура воды в градусах ( Tv ) со множеством значений от 0 до 90. На выходе определяется чёткая переменная - время стирки в минутах ( Dlt ) со множеством значений от 0 до 150. С массой белья связана лингвистическая переменная «количество белья» со значениями «много» и «мало». С температурой связана лингвистическая переменная «температура воды» со значениями «высокая» и «низкая». Со временем стирки связана лингвистическая переменная «длительность», имеющая значения «высокая» и «малая».

БЗ состоит из двух правил:

R 1 : ЕСЛИ <количество_белья> = <много> И

<температура_воды> = <высокая>, ТО

<длительность> = < высокая>

R 2 : ЕСЛИ <количество_белья> = <мало> И

<температура_воды> = <низкая>, ТО

<длительность> = < малая>.

Метод фазификации переменных осуществляется с помощью соответствующих МЗ.

МЗ Выполнение нечёткого вывода для стиральной машины

ранг	имя	наименование
0	NzImFn	Назначение имени функции
1	NzZnPr22	Назначение значения низкая переменной температура воды
1	NzZnPr21	Назначение значения мало переменной количество белья
1	NzZnPr11	Назначение значения много переменной количество белья
1	NzZnPr12	Назначение значения высокая переменной температура воды
2	MFuzif21	Метод фазификации 1 переменной 2 правила
2	MFuzif22	Метод фазификации 2 переменной 2 правила
2	MFuzif12	Метод фазификации 2 переменной 1 правила
2	VpR1	Выполнение правила R1
2	VpR2	Выполнение правила R2
2	MFuzif11	Метод фазификации 1 переменной 1 правила
3	MRsTnR2	Метод расчёта Т-нормы для правила R2
3	MRsTnR1	Метод расчёта Т-нормы для правила R1
4	RsDlml	Расчёт малой длительности
4	RsDlvs	Расчёт высокой длительности

Входные свойства имя наименование тип значение

Mass Масса, кг REAL 0.7

Tv Температура, град REAL 20.1

Выходные свойства имя наименование тип значение

Dlt Длительность, мин REAL 37.5

4    Нейросетевые модели знаний

Для построения ИС традиционно применяются два основных подхода. Первый основан на правилах. При этом подходе необходимо заранее знать весь набор закономерностей, описывающих предметную область. Он детально описан в [14]. При использовании другого подхода, основанного на примерах, надо иметь достаточное количество примеров для настройки адаптивной системы с заданной степенью достоверности. Нейронные сети (НС) представляют собой пример такого подхода. С точки зрения экспертного программирования НС может рассматриваться как механизм одного из правил [13]. При построении БЗ такое правило может использоваться совместно со всеми другими типами правил. Комбинированный подход обеспечивает получение правил на основе примеров, сохранённых в базе данных (БД). Это – извлечение знаний из данных.

Искусственные нейронные сети НС предназначены для решения широкого круга задач: принятия решений, распознавания образов, идентификации, прогнозирования, оптимизации, управления сложными объектами. Применительно к рассматриваемой тематике наибольший интерес представляет применение НС для принятия решений и управления. Эта задача близка к задаче классификации. Классификации подлежат ситуации, характеристики которых поступают на вход НС. На выходе сети при этом должен появиться признак решения, которое она приняла. При этом в качестве входных сигналов используются различные критерии описания состояния управляемой системы.

Формальным нейроном называется элемент, используемый в узлах НС. Ему может быть поставлена в соответствие структурная схема, представленная на рисунке 3.

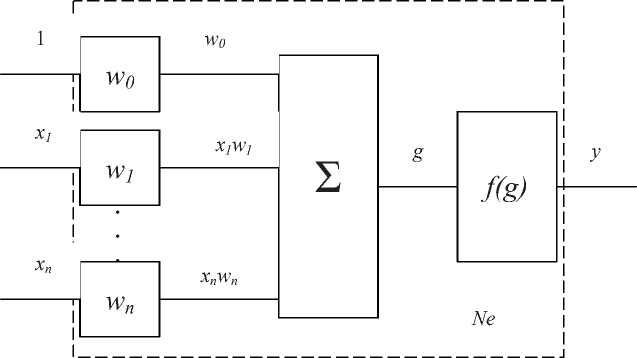
Рисунок 3 - Структурная схема формального нейрона

Схема формального нейрона включает n входных блоков умножения на коэффициенты w i , один сумматор и выходной блок функционального преобразования. Функция, которую реализует выходной блок, получила название функции активации. Коэффициенты w i получили название синаптических коэффициентов или коэффициентов межнейронной связи.

Формальный нейрон может быть представлен с помощью двух МЗ. Первый реализует входные блоки и сумматор, а второй – функцию активации. В качестве простого примера модуля, осуществляющего расчёт взвешенной суммы входов нейрона, приведено внешнее представление МЗ RSNeur11. Модуль не имеет предусловия запуска. Такой модуль запускается на исполнение, когда будут определены все входные свойства. В качестве входных свойств выступают входные переменные и синаптические коэффициенты. Выходом модуля является взвешенная сумма входов нейрона, которая вычисляется по формуле.

МЗ: RSNeur11 - Расчёт взвешенной суммы входов нейрона 1 слоя 1

Предусловия запуска имя наименование тип условие

Входные свойства

имя	наименование	тип	значение
w14	Вес связи 14	REAL
x_2	Входная переменная 2	REAL
x_0	Входная переменная 0	REAL
x_3	Входная переменная 3	REAL
x_8	Входная переменная 8	REAL
x_9	Входная переменная 9	REAL
w11	Вес связи 11	REAL
w13	Вес связи1 3	REAL
w12	Вес связи 12	REAL
x_1	Входная переменная 1	REAL
w16	Вес связи 16	REAL
w17	Вес связи 17	REAL
w15	Вес связи 15	REAL
w19	Вес связи 19	REAL
w18	Вес связи 18	REAL
x_6	Входная переменная 6	REAL
x_4	Входная переменная 4	REAL
x_5	Входная переменная 5	REAL
x_7	Входная переменная 7	REAL

Механизм - Формула s11=x_0+x_1*w11+x_2*w12+x_3*w13+x_4*w14+x_5*w15+x_6*w16+x_7*w17+x_8*w18+x_9*w19

Выходные свойства

имя	наименование	тип	значение
s11	Взвешенная сумма входов нейрона 1 слоя 1	REAL

Вычисление значения функции активации осуществляется модулем RFNeur11. Модуль имеет предусловие, которое определяет вид выбранной функции. В данном случае используется логистическая функция. Входные свойства модуля включают параметр функции активации и взвешенную сумму входов нейрона. Параметр функции активации выбирается из БД со свойствами сети нейронов, а взвешенная сумма входов вычисляется предыдущим МЗ.

МЗ: RFNeur11 - Расчёт функции активации нейрона 1 слоя 1 Предусловия запуска имя наименование тип условие

VidAktFn$ Вид активационной функции STRING логистическая

Входные свойства имя наименование тип значение a_ Параметр функции активации REAL s11 Взвешенная сумма входов нейрона 1 слоя 1 REAL

Механизм - Формула y11 = 1/(1 + 2.71828^(-a_*s11))

Выходные свойства имя наименование тип значение y11 Активационная функция нейрона 1 слоя 1 REAL

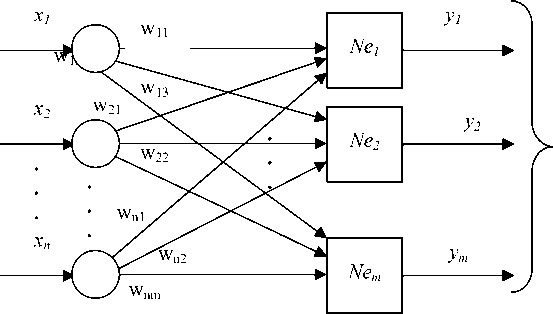
Приведённые выше два МЗ реализуют формальную модель нейрона. С помощью описанной технологии возможно генерировать модели с другими количествами входных переменных и синаптических коэффициентов, а также с другими активационными функциями и с другими моделями нейронов. Хотя один нейрон и способен выполнять простейшие процедуры распознавания, эффективность нейронных вычислений проявляется в нейронных сетях. Простейшая сеть состоит из группы нейронов, образующих слой (см. рисунок 4).

X <

Y

Рисунок 4 - Простейшая однослойная нейронная сеть

Вершины-круги, представленные на рисунке 4, предназначены для распределения входных сигналов. Каждый элемент из множества входов X соединён с каждым искусственным нейроном Ne i отдельной связью, которой приписан вес (синаптический коэффициент). Удобно считать веса элементами матрицы W . Матрица имеет n строк и m столбцов, где n – число входов, а m – число нейронов.

Для построения продукционной модели НС генерируется метод, состоящий из набора МЗ. Этот метод в дальнейшем может использоваться в качестве модуля в сложных БЗ.

На рисунке 5 представлена функциональная модель НС в соответствии со стандартом IDEF0 . Функция модели заключается в вычислении компонент y j вектора Y . Для этого в качестве входных переменных используются компоненты x i вектора X. Механизмом выполнения этой функции является МЗ и элементы матрицы весов W , которые хранятся в БД. НС характеризуется параметрами: количество входов и выходов, количество слоёв и нейронов в каждом слое, параметры активационной функции.

Ниже приведён пример внешнего представ

Параметры сети

X

Вычисление

нейронной сети

Модуль знаний

Y

Рисунок 5 - Функциональная модель нейронной сети

ления автоматически сгенерированного метода расчёта простой однослойной НС, включающей три нейрона, десять входных и три выходных переменных.

МЗ RsNeurNet - Расчёт нейронной сети

ранг	имя	наименование
0	VzPrNet	Вызов параметров сети
0	NUstN	Начальная установка номера входной переменной
0	NUstPer	Начальные установки переменных
1	MVvW	Метод ввода весовых коэффициентов 1-го слоя
2	RSNeur21	Расчёт взвешенной суммы входов нейрона 2 слоя 1

2    RSNeur11 Расчёт взвешенной суммы входов нейрона 1 слоя 1

• 2    RSNeur31 Расчёт взвешенной суммы входов нейрона 3 слоя 1

• 3   RFNeur21 Расчёт логистической активационной функции нейрона 2 слоя1

• 3   RFNeur11 Расчёт логистической активационной функции нейрона 1 слоя1

• 3   RFNeur31 Расчёт логистической активационной функции нейрона 3 слоя1

• 4    FrOut11  Формирование выхода однослойной сети с одним нейроном

• 4    FrOut12  Формирование выхода однослойной сети с двумя нейронами

• 4    FrOut13  Формирование выхода однослойной сети с тремя нейронами

Входные свойства

имя	наименование	тип	значение
x_10	Входная переменная 10	REAL
x_8	Входная переменная 08	REAL
x_7	Входная переменная 07	REAL
x_4	Входная переменная 04	REAL
x_6	Входная переменная 06	REAL
x_5	Входная переменная 05	REAL
x_9	Входная переменная 09	REAL
x_2	Входная переменная 02	REAL
x_3	Входная переменная 03	REAL
x_1	Входная переменная 01	REAL

Выходные свойства

имя	наименование тип значение
y_1	Выходная переменная 1 REAL 0.
y_2	Выходная переменная 2 REAL 0
y_3	Выходная переменная 3 REAL 0

МЗ метода автоматически ранжируются в порядке определения необходимых для их работы переменных. В данном случае в ранге 0 размещаются модуль вызова из БД параметров сети и служебные модули начальных установок переменных. Ранг 1 включает метод ввода весовых коэффициентов, вызываемых из БД.

Ранг 2 состоит из модулей расчёта взвешенных сумм входов всех нейронов, а ранг 3 – из модулей расчёта активационных функций для этих нейронов. В заключительном ранге 4 располагаются модули формирования выходных переменных.

Важнейшим компонентом построения БЗ на основе НС является обучение. В качестве примера построения алгоритма обучения рассмотрен метод обучения, названный δ -правило [5]. Пусть имеется обучающая выборка, состоящая из пар векторов ( X^k , Y^k ), k = 1, 2, … p . НС называется обученной на данной обучающей выборке, если при подаче на входы сети каждого вектора X^k на выходах всякий раз получается соответствующий вектор Y^k . Обучение заключается в итерационной подстройке матрицы весов W , последовательно уменьшающей ошибку в выходных векторах. Алгоритм включает следующие шаги.

Шаг 0. Проинициализировать элементы весовой матрицы W случайными значениями.

Шаг 1. Подать на входы один из входных векторов X^k и вычислить его выход Y^k .

Шаг 2. Если выход правильный ( Y = Y^k ), перейти на шаг 4. Иначе, вычислить вектор ошибки – разницу между заданным и полученным значениями выхода: δ = Y^k – Y.

Шаг 3. Матрица весов модифицируется по следующей формуле: w^t+1 ij = w^t ij + ν·δ·x i . Здесь t и t +1 – номера соответственно текущей и следующей итераций; ν – коэффициент скорости обучения (0< ν ≤1); x i – i -я компонента входного вектора X^k ; j – номер нейрона в слое.

Шаг 4. Шаги 1–3 повторяются для всех обучающих векторов. Обучение завершается, когда сеть перестаёт ошибаться.

МЗ ObNeurNet - Обучение нейронной сети ранг имя                   наименование

• 0    NUstN Начальная установка номера входной переменной

• 0    NUstNc Начальная установка номера цикла обучения

• 0    VzPrNet Вызов параметров сети

• 1    PerAdrOb Переадресация цикла обучения

• 1    VvNObVb Ввод номера обучающей выборки

• 2    MVvXob Метод ввода входных переменных обучающей выборки

• 2    MInitW Метод инициации весов матрицы W

• 2    MVvYob Метод ввода выходных переменных обучающей выборки

• 2    NzFnClOb Назначение признака конца цикла обучения

• 3    MModW Метод модификации матрицы весов

В ранг 0 входят служебные МЗ, которые не включаются в тело цикла обучения сети. Они осуществляют начальные значения переменных, необходимых для дальнейшего использования и вызов параметров сети, включающих количества входных и выходных переменных, слоёв нейронов, а также параметр функции активации.

В ранг 1 входят МЗ, осуществляющие переадресацию цикла обучения и ввод номера обучающей выборки.

В ранг 2 входят следующие МЗ. Структурированный модуль инициации весов матрицы W , выполняющий функции шага 0. Этот модуль выполняется однократно в начале цикла обучения. Два модуля ввода входных и выходных переменных обучающей выборки, выполняющие функции шага 1. Модуль назначения признака конца цикла обучения, выполняющий функции шага 2.

В ранг 3 входит модуль модификации матрицы весов, выполняющий функции шага 3.

Заключение

Базовыми принципами мягких вычислений являются: терпимость к неточности, неопределённости и частичной истинности, робастности, низкой стоимости решения и лучшего согласия с реальностью. Интеграция жёстких вычислений с мягкими может осуществляться посредством создания синергетических БЗ.

В работе представлен подход к созданию синергетических БЗ в формате структурированных МЗ.