Синергия гуманитарного и математического знания как педагогическое условие решения междисциплинарных проблем

В эпоху становления новой коммуникативной парадигмы постнеклассической науки, ориентированной на междисциплинарный подход и межкультурный диалог, требуется взвешенно и конструктивно подойти к решению задач, стоящих перед Россией и мировым сообществом в XXI в. – интеграции науки и культуры, технического и гуманитарного знания, совмещения современных достижений технического прогресса с культурными ценностями. Сегодня мир должен опираться на синергию знания, диалог разных культур. Данное направление представляется весьма актуальным и перспективным, поскольку имеет выходы в различные исследовательские и образовательные области.

Одним из наиболее успешных и плодотворных направлений исследований в последние десятилетия стала теория самоорганизации, или синергетика. Синергетический подход предполагает глубокое предметное знание, философский анализ, теорию и практику моделирования. Исходным совокупным онтологическим основанием процесса синергии выступают интегративность, сложносистемность, взаимосвязанность и взаимозависимость деятельности; гносеологическим основанием – научная картина мира как форма систематизации знаний, отражающая влияние философских категорий и принципов на конкретные научные теории.

Синергетический подход имеет свой достаточно специфический терминологический язык, одним из ключевых понятий которого является «синергия». Синергия рассматривается как общенаучный феномен, распространившийся на многие аспекты жизни и создавший информационное описание мира. Данный термин означает рост эффективности деятельности в результате соединения, интеграции, слияния отдельных частей в единую систему за счет системного эффекта – эмерджентности. В философии под синергией понимают создание целостного знания на основе соединения исторически сложившихся различных подходов, методов [1].

В последние десятилетия идеи взаимного проникновения гуманитарных и математических методов стали активно развиваться во всех областях знаний [2; 3]. Для эффективного решения междисциплинарных проблем, предполагающих адаптацию современных достижений науки в образовательный процесс, необходим комплекс педагогических условий с доминантой синергии математических и гуманитарных знаний.

В исследовании выделены следующие педагогические условия решения междисциплинарных проблем в контексте интегративного обучения:

– разработка совместных проектов исследования из различных дисциплинарных областей;

– обучение целенаправленному математическому моделированию проблемных ситуаций будущей профессиональной деятельности в процессе вузовской подготовки специалиста;

• –    постановка проблемных междисциплинарных задач, которые имеют решение за пределами изучаемого курса;

• –    обеспечение поиска и отбора необходимой информации в различных предметных сферах;

• –    разработка банка междисциплинарных задач для глубокой интеграции математического и гуманитарного знания;

• –    реализация системы форм организации, средств, методов и приемов обучения, способствующих междисциплинарной интеграции;

  – организация учебных занятий, мотивирующих студентов к свободному поиску информации и обращению к заранее созданным банкам данных при выполнении междисциплинарных учебных и научно-исследовательских заданий.

Выполнение перечисленных требований приводит к раскрытию индивидуальных особенностей, актуализации проявления творческой самостоятельности в образовательном процессе, формированию и развитию общекультурных и профессиональных компетенций, а также повышению учебной и профессиональной мотивации обучаемых.

Обзор литературы

Одной из актуальных междисциплинарных проблем образования представляется задача анализа и сравнения стилей текстовых произведений. Ее решение возможно с использованием как гуманитарных, так и математических средств. Математические методы позволяют получить не только количественные, но и качественные выводы в филологических исследованиях. В литературоведческой практике проверка текстов на близость стилей необходима для установления в спорных случаях подлинного авторства литературных произведений, особенно удаленных временем. В качестве примеров можно привести споры об авторстве некоторых произведений У. Шекспира, отдельных анонимных и псевдонимных публицистических статей, приписываемых Ф. М. Достоевскому, стихотворных текстов М. Ю. Лермонтова, прозаических произведений М. Е. Салтыкова-Щедрина, М. А. Шолохова и др.

Вопросами проверки текстов произведений на близость стилей с применением формально-количественных методов в российской и зарубежной науке занимались А. А. Марков [4; 5], Н. А. Морозов [6], В. Э. Сеземан [7], В. П. Фоменко, Т. Г. Фоменко, В. Фукс [8],

Д. В. Хмелев, Г. Хетсо [9], О. Г. Шевелев1 и др. Одним из первых исследователей, который применил математические методы к анализу литературных текстов, был А. А. Марков [5]. В 1913 г. он провел анализ распределения гласных и согласных среди первых 20 000 букв романа А. С. Пушкина «Евгений Онегин».

Несмотря на наличие ряда исследований по проверке близости стилей текстов, остается немало не исследованных или мало исследованных областей. Если рассматривать историю атрибуции текста с применением формальных методов анализа глубже, то можно заметить, что ни в одной из существующих ныне работ практически не поднимался вопрос о применении вероятностно-статистического метода для анализа изменения (сохранения) стиля автора, тексты которого были созданы в разные периоды жизни под воздействием объективных социокультурных факторов.

Анализ биографий многих писателей XIX–ХХ вв. установил, что под давлением революций и всякого рода общественных волнений авторам приходилось совершать вынужденные переезды. Могла ли изменяющаяся социокультурная среда влиять на стилевую специфику автора? Речь идет о представителях так называемой «белой» эмиграции, покинувших Россию после октябрьских событий 1917 г. (И. А. Бунин, Б. К. Зайцев, А. М. Ремизов, И. С. Шмелев и др.), и не вернувшихся на Родину. В связи с этим остро встает проблема не только совершенствования методов сравнения текстов, но и обучения им студентов.

Материалы и методы

Ведущим методом настоящего исследования стал метод экспериментального исследования, его констатирующий, поисковый и обучающий этапы. Рассмотрим, как были реализованы эти этапы при обучении студентов различных направлений подготовки. На первом этапе студентам-филологам и студентам-математикам старших курсов, обучающимся по направлению подготовки «Прикладная математика и информатика», была предложена профессиональная и соответственно прикладная задача на поиск методов анализа и сравнения авторских стилей. Сравнение конкретных текстов возможно на основе совокупности признаков, отражающих существенные свойства авторского стиля. К идентифицирующим признакам можно отнести статистические характеристики (частотность слов, букв, их сочетаний, количественное использование определенных частей речи, синтаксических конструкций и т. д.). В науке установлено, что вероятность появления сочетания пар символов различной природы в тексте отдельных авторов подчиняются некоторым устойчивым закономерностям. Объектом исследования были выбраны произведения выдающегося русского прозаика, лауреата Нобелевской премии И. А. Бунина.

Студенты-филологи задачу изменения стиля автора под влиянием социокультурной среды решали на примере двух произведений И. А. Бунина, первого – раннего периода его творчества «Деревня» (1910), второго – позднего творческого этапа «Жизнь Арсеньева» (1927–1929).

Приведем решение проблемы студентами-филологами.

Повесть «Деревня» создавалась И. А. Буниным под воздействием событий русско-японской войны, первой русской революции (1905 г.), последовавшей за ней правительственной реакции, и отражала предчувствие новых социальных потрясений, накал которых чувствовался в общественной и политической жизни страны. Писатель, живший в то время в центральной России, прекрасно знал тяготы крестьянского существования, проблемы мелкопоместного дворянства. Его представления о русском характере соотносились с мрачной картиной современной российской действительности. Отсюда стиль писателя определяется наиболее часто встречающимися биграммами { га, ха, да, та, зс, бп, … }, в которых зафиксированы тревожные переживания художника слова.

Роман «Жизнь Арсеньева» создавался в иной социокультурной атмосфере. Летом 1927 г. во французский городок Грасс к И. А. Бунину приехала Галина Кузнецова, ставшая, как известно, последней музой писателя. Ситуация влюбленности и великолепие окружающей природы рождало состояние умиротворения, которое отразилось в стиле произведения. Автобиографическое произведение наполнилось многочисленными воспоминаниями, ностальгическими настроениями, в которых не было надрыва и необратимой тоски. Наложение достаточно сильных экспрессивных переживаний на не менее активные положительные эмоции привело к созданию размеренного, почти лирического стиля. В условиях указанной социокультурной ситуации наиболее эффективными в репрезентации авторского замысла оказываются такие буквенные сочетания, как {ле, ло, ме, ми, ро, рл,}. Они со всей очевидностью позиционируются как более благозвучные, плавные, размеренные, чем те, которые выявлены в тексте повести «Деревня». Сравнение «ранних» и «поздних» буквосочетаний позволяет утверждать, что под влиянием социокультурной среды русского зарубежья 1920-х гг. произошли качественные изменения стиля выдающегося писателя И. А. Бунина.

Под руководством преподавателей студентами-математиками для реше-ния поставленной прикладной задачи была применена технология марковских цепей для анализа пар букв в их естественных последовательностях в тексте с целью установления устойчивости авторского стиля. Исходной предпосылкой построения модели было предположение, что в распоряжении имеются достаточно длинные фрагменты (не более 100 000 символов) прозаических произведений одного автора на русском языке, написанные в разные периоды жизни. Из текстов произведений раннего периода отдельного автора выбирался один контрольный. Осуществлялся подсчет чисел вхождений каждой n² возможных пар букв (биграмм) в достаточно длинных открытых текстах T = 1 1 t 2 ^t_l , составленных из букв алфавита { a₁, a₂, ..., a_n }. Вычислялась матрица переходных частот употреблений пар букв. По произведению более позднего периода аналогично строилась вторая экспериментальная матрица переходных частот. С применением χ² -критерия Пирсона устанавливалась значимость различий между переходными частотами матриц произведений раннего и позднего периодов. Если вычисленная оценка вероятности высока, то стиль автора под воздействием внешних факторов не изменился, и наоборот. Такой метод, по их мнению, оказался достаточно точным для естественно-языковых текстов.

Для построения матриц переходных частот были выбраны те же два произведения И. А. Бунина. Анализ сочетаемости букв (биграмм вида гласная – согласная, гласная – гласная, согласная – согласная) проводился с использованием матриц переходных вероятностей размерностью 33^33. Полученная первая экспериментальная матрица была соотнесена с экспериментальной матрицей, составленной по тексту позднего произведения при помощи х ²-критерия Пирсона. Расхождение между частотами на 10 % уровне значимости позволило сделать вывод о несовпадении двух экспериментальных распределений. Следовательно, стиль автора изменился.

В дальнейшем для проверки эффективности модели сравнения авторского стиля и степени устойчивости полученных результатов нами была разработана программа «Статистический стилевой анализатор», реализованная на языке C#. Особенность данной программы заключается в том, что с ее помощью можно выявить степень изменения авторского стиля на основе частоты встречаемости пар букв в их естественных последовательностях в тексте. Такой подход позволяет более точно учитывать роль, специфику распределения в сопоставляемых текстах стилистических, лексических и других признаков при классификации произведений авторов по стилю, а также при решении задач, связанных с определением авторства.

Представим алгоритм работы анализатора.

периоду творчества автора. Нажимаем кнопку «Составить матрицу частот» для двух текстов (рис. 1). Следует уточнить, что для корректной работы программы вводимый в поле текст дожен иметь размер не более 100 000 символов .

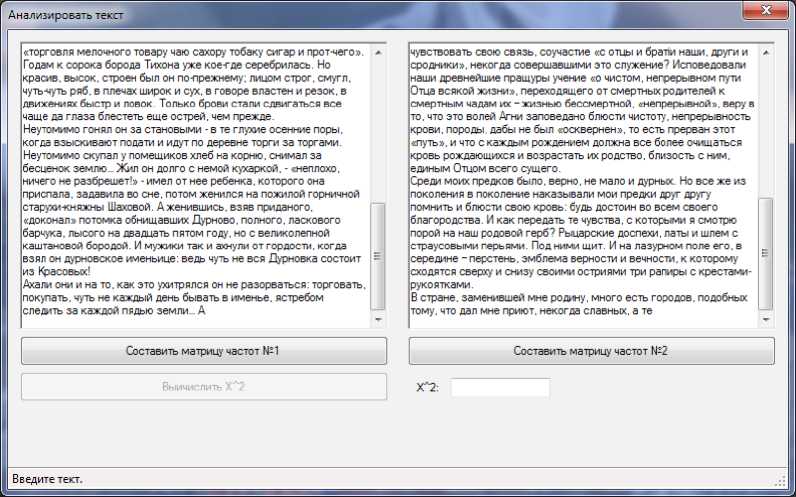
Р и с. 1. Первый этап алгоритма программы анализатора

F i g. 1. 1st step of the analyser programme algorithm

2. После того, как две различные матрицы с частотами сформированы, нажимаем кнопку «Вычислить χ²». Получаем значение Х²_эмп=1189,305 (рис. 2), что существенно больше Х²_кр=1012,425 , а это значит, что мы вынуждены отклонить нулевую гипотезу и признать, что авт ^р орский стиль И. А. Бунина изменился после эмиграции во Францию.

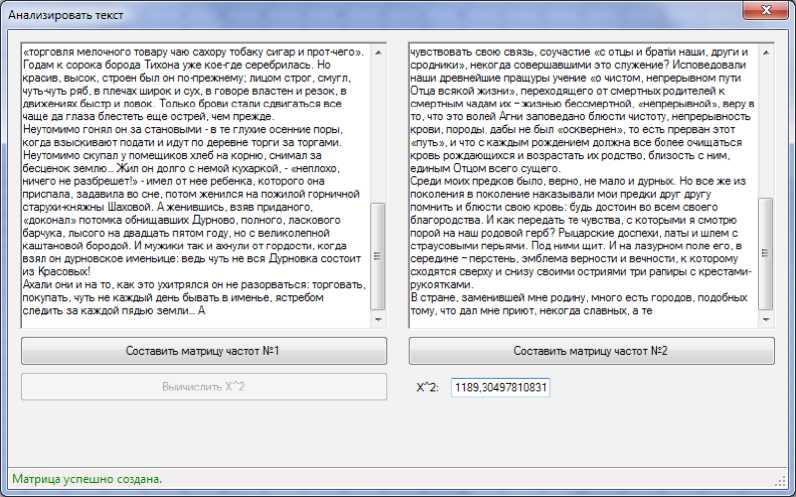
Р и с. 2. Второй этап алгоритма программы анализатора

F i g. 2. 2st step of the analyser programme algorithm

Следует заметить, что контрольная проверка адекватности работы разработанной модели осуществлялась на произведениях совершенно различных авторов. В качестве первого отрывка выступал роман М. А. Булгакова «Мастер и Маргарита», второго – роман «Лето Господне» И. С. Шмелева. Были сформированы основная проверяемая Н0={автор текста не изменился} и альтернатив- ная гипотезы Н1 = {авторы произведений различны}. Запускаем программу и вводим отрывки в поля «Текст № 1» и «Текст № 2» соответственно. Составляем матрицы переходных вероятностей, вычисляем Х2эмп. Конечный результат работы алгоритма представлен на экране: Х2эмп=1487,477>Х2кр=1012,425 (рис. 3). Полученный результат дает основания для отклонения основной гипотезы Н0 и принятия ее альтернативы.

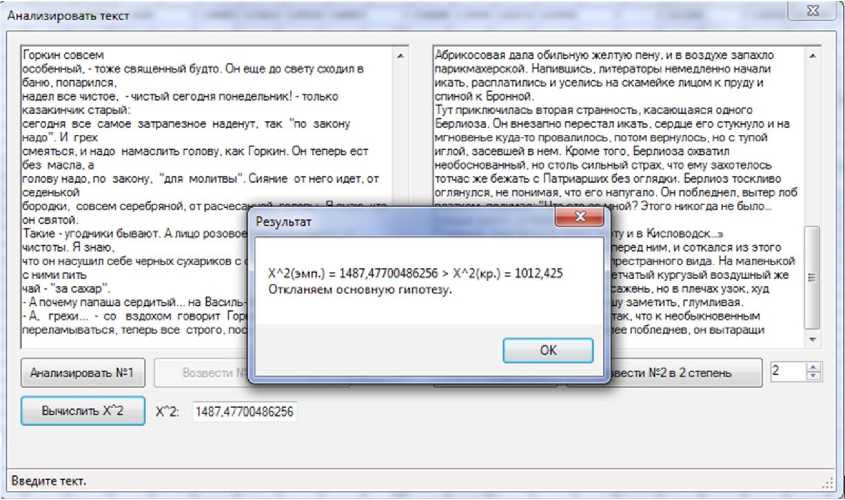
Р и с. 3. Результат проверки авторства

F i g. 3. The result of the authorship varification

Разработанный программный продукт может успешно применяться студентами-филологами при решении профессиональных задач, связанных с анализом стилевых особенностей, а также в лекционных курсах и на практических занятиях по стилистике, компьютерной лингвистике, лексикологии, русской и зарубежной литературе, по общим проблемам классификационного анализа.

Результаты исследования

В результате поискового этапа эксперимента было выявлено, что предложенная студентами-математиками вероятностная модель анализа и срав- нения стилей текстовых произведений, а также ее программная реализация не только количественно подтверждает полученные результаты качественного анализа студентами-филологами, но устанавливает их статистическую достоверность. Следовательно, необходим диалог математических и гуманитарных знаний, который обогатит представление обучаемых о научном подходе к исследованиям, о русских художниках слова, об особенностях творческого процесса как сложного духовного явления.

Это послужило обоснованием актуальности проектирования и внедрения в учебный процесс интегративного курса

«Математические методы в языкознании». С помощью такого специального курса студентам-филологам можно сформировать системное знание на основе диалога культур, навыки использования современного математического аппарата в решении профессиональных задач в соответствии со спецификой профиля; эффективно развить интегративные качества личности на основе теории фундирования в опоре на поэтапное расширение и углубление опыта [10]; выработать представления о роли и месте математики в современной цивилизации и в мировой культуре.

Реализация выделенных нами педагогических условий решения междисциплинарных проблем в контексте интегративного обучения позволила определить оптимальную структуру интегративного курса «Математические методы в языкознании», представленную следующими модулями:

• 1.    Становление современной математики как новой культурной парадигмы. Математика как часть общечеловеческой культуры. Взгляды на математику выдающихся деятелей прошлого и настоящего, их оценка роли и места математики, информатики и их методов в решении профессиональных задач из различных сфер человеческой деятельности.

• 2.    Основные математические понятия в языкознании.

  • 2.1.    О парадигме линейности. Понятие линейного пространства. Феномен нелинейного. Понятие фрактала. Семантические и фонетические фракталы в языке. Законы Ципфа в лингвистике.

  • 2.2.    Основные определения и парадоксы теории множеств. Элементы, множества, операции над множествами, мощность множества. Бинарные отношения. Эквивалентность. О числовых множествах. Конечные и бесконечные множества. Роль теории математических множеств в установлении падежей русского языка (по А. Н. Колмогорову). Падеж как класс эквивалентных семантических состояний.

  • 2.3.    Культурологические основы появления математического анализа. Исто-

• рическая необходимость возникновения в математике понятий последовательности, функции и их пределов. Зависимость между единицами языка. Последовательности языковых и иных знаков в лингвистике. Понятия производной, определенного интеграла и их приложения. Понятие о формуле Тейлора. Феномен нелинейности. Ряды – основа приближенных вычислений. Феномен бесконечного.

• 2.4.    Основные понятия дискретной математики. Элементы математической логики. Таблицы истинности. Некоторые формулы алгебры высказываний. Об исчислении предикатов и о нечеткой логике. Поиск логических структур в текстах Священного писания, афористических высказываний великих мудрецов, текстах народного фольклорного творчества.

• 2.5.    Элементы комбинаторики. Место комбинаторной лингвистики в структуре науки о языке. Сочетаемость в образовании словоупотреблений в поэзии, публицистике и художественной речи.

• 3.    Математические методы в языкознании.

  • 3.1.    Феномен случайного в различных сторонах человеческой деятельности. Отношение искусства и литературы к случайному событию. Исторические и культурные предпосылки появления теории вероятностей. Элементы теории вероятностей. Понятие случайного события и их виды. Алгебра случайных событий. Классическое, статистическое, геометрическое и эвристическое определения понятия вероятности. Генезис понятия вероятности (логическая, пропен-ситивная, субъективная) в библейских преданиях и историко-художественных текстах.

  • 3.2.    Математика как один из инструментов описания окружающего мира. Сравнение языка математики с языком литературы, искусства, естественных наук. Принципы построения математических моделей. Математическое моделирование закономерностей предметных областей. О линейных моделях математического моделирования. Решение профессиональных задач на установление

идентичности текстовых произведений методом моделирования.

Обсуждение и заключения

Таким образом, синергия матема-тического и гуманитарного знания оказывается весьма продуктивной как в научно-исследовательской деятельности обучаемых, так и в образовательном процессе через представленный и апробируемый комплекс педагогических условий посредством разработанного интегративного курса для студентов-филологов. Предложенный учебный материал может быть полезен для студентов, обучающихся по направлению подготовки «Филология», «Прикладная филоло -гия», «Журналистика», «Педагогиче- ское образование (профиль русский язык и литература / иностранный язык)». Более того, он представляет определенный интерес и для студентов, обучающихся по направлению подготовки «Прикладная математика и информатика», некоторым инженерно-техническим специальностям. Приведенную в данной статье профессиональную задачу и ее аналоги целесообразно включать как в интегративные материалы и курсы, так и в совместные научно-исследовательские проекты. Их решение способствует развитию учебной и профессиональной мотивации студентов и, следовательно, повышению эффективности и качества образования – гарантируемому эффекту синергии гуманитарного и математического знания.

СПИСОК

ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

• 1.    Дворяткина С. Н., Лопухин А. М. Этапы становления синергии математического образования в контексте мирового и отечественного опыта // Continuum. Математика. Информатика. Образование. 2016. № 2. С. 64-69. URL: http://elibrary.ru/item.asp?id=27289448 (дата обращения: 25.09.2016).

• 2.    Dvoryatkina S. N., Dyakina А. А. On variability of authors’ style under the influence of the socio-cultural environment in the context of dialogue of natural scientific and humanitarian cultures // Mediterranean journal of social sciences MCSER Publishing, Rome-Italy. 2015. Vol. 6, no. 5 S4. Pp. 167-171. URL: http://elibrary.ru/item.asp?id=24553891 (дата обращения: 25.09.2016).

• 3.    Розанова С. А., Смирнов Е. И . Психолого-педагогические проблемы преподавания математики студентам-гуманитариям и в школах с профильными гуманитарными классами // Труды Международной научной конференции «Образование, наука и экономика в вузах и школах. Интеграция в международное образовательное пространство». Армения, Горис, 2015. С. 544–550. URL: http://elibrary.ru/item.asp?id=24268034 (дата обращения: 25.09.2016).

• 4.    Марков А. А. Об одном применении статистического метода // Известия Императорской Академии наук. Сер. 6. 1916. Т. 10, № 4. С. 239–242. URL: http://www.textology.ru/library/book . aspx?BookId=8&textId=2 (дата обращения: 25.09.2016).

• 5.    Марков А. А. Пример статистического исследования над текстом «Евгения Онегина», иллюстрирующий связь испытаний в цепь // Известия Императорской Академии наук. Сер. 6. 1913. Том 7, вып. 3. С. 153–162. URL: http://books.e-heritage.ru/book/10085763 (дата обращения: 25.09.2016).

• 6.    Морозов Н. А. Лингвистические спектры. Средство для отличения плагиатов от истинных произведений того или иного известного автора: Стилеметрический этюд // Известия отд. русского языка и словесности Имп. Акад. Наук. 1915. Т. 20, кн. 4. С. 93-127. URL: http://www.textology . ru/library/book.aspx?bookId=1&textId=3 (дата обращения: 25.09.2016).

• 7.    Сеземан В. Э. «Лингвистические спектры» г. Морозова и Платоновский вопрос // Известия отделения русского языка и словесности Императорской Академии наук. 1918. Т. 22, кн. 2. С. 21–34.

• 8.    Фукс В. По всем правилам искусства: точные методы в исследованиях литературы, музыки и изобразительного искусства // Искусство и ЭВМ / Под ред. Р. Х. Зарипова. М. : Мир, 1975. С. 134–356.

• 9.    Хетсо Г. Проблема авторства в романе «Тихий дон» // Scando-slavica. 1978. Т. 24. С. 91-105.

• 10.    Смирнов Е. И. Фундирование как методология и инновационный механизм профессионального становления педагога // Научные труды SWORLD. 2013. № 4. С. 76–84. URL: http://www.

Поступила 06.10.2016; принята к публикации 07.12.2016; опубликована онлайн 30.03.2017.

Об авторе :

Дворяткина Светлана Николаевна, профессор кафедры математики и методики ее преподавания ФГБОУ ВО «Елецкий государственный университет им. И. А. Бунина» (399770, Россия, г. Елец, ул. Коммунаров, д. 28), доктор педагогических наук, ORCID: ,

Дякина Анжелика Александровна, профессор кафедры философии и социальных наук ФГБОУ ВО «Елецкий государственный университет им. И. А. Бунина» (399770, Россия, г. Елец, ул. Коммунаров, д. 28), доктор филологических наук, ORCID: ,

Розанова Светлана Алексеевна, профессор кафедры высшей математики ФГБОУ ВО «Московский технологический университет (МИРЭА)» (119602, Россия, г. Москва, пр-т Вернадского, д. 78), доктор педагогических наук, профессор, ORCID: ,

Заявленный вклад авторов :

Дворяткина Светлана Николаевна – развитие теоретико-методологических основ исследования; разработка математической модели идентификации текстов и ее программной реализации на С#; участие в составлении программы интегративного курса; написание текста.

Дякина Анжелика Александровна – постановка профессиональной проблемы анализа и сравнения стилей текстовых произведений, ее лингвистическое решение; определение перспектив исследования в гуманитарных областях.

Розанова Светлана Алексеевна – постановка научной проблемы статьи и определение основных направлений ее решения, участие в разработке программы интегративного курса; актуализация практических приложений результатов исследования в различных формах образовательного процесса; решение административных вопросов по подготовке текста.

Все авторы прочитали и одобрили окончательный вариант рукописи.