Single and Multi-Area Optimal Dispatch by Modified Salp Swarm Algorithm

Published Online June 2020 in MECS

During past few decades researchers had paid more attention to nature inspired optimization techniques for solution of different types of complex constrained real world problems. This may due to population based and involvement of random operator in almost all NI techniques, which helps to find out global or near global solution in single run for either nature of problem i.e. non-convex with multiple minima, discontinuous or non-differentiable function [1-5]. These methods are inspired by natural process and broadly classified in five categories based on source of inspiration: evolution, swarm intelligence, human intelligence, ecology or physical science [6].

Economic dispatch (ED) is one of the important optimization issues in power system operation. Goal of ED is to allot the load demand among the committed power generating unit in most economical way while satisfying all the physical and operational constraints too[7,8]. Solution of different types of single area ED problems were presented using either classical solution/ NI based approach by various researchers [9-16]. Among

NI technique evolutionary programming (EP) [9], differential evolution (DE) [10], harmony search (HS) [11], biogeography based optimization (BBO) [12], artificial bee colony (ABC) [13], crow search algorithm (CSA) [14], hybrid PSO-GSA [15], flower pollination algorithm (FPA) [16], were applied to solve ED problems. A detailed survey of particle swarm optimization (PSO) and application to ED problem is presented in ref. [17].

Multi-area ED (MAED) is the expanded version of ED where each area having several power generating units connected with each other via tie line. Also transmission line (tie-lines) has various complexities related to costing, power wheeling and transfer capability. Each area has been controlled by independent system operator (ISO) and has its own pattern of load variation as well as power generation characteristics. There are also issues related to environmental pollution and global warming, minimization of harmful emission from power plant considered as other objective. The MAED problem has become much complex to solve due additional tie line capacity constraints along with the above mentioned operational constraints [18-29]. Considering new regulation for excessive generated greenhouse gases, a combination of MAED and constraints on emission has come in to picture called multi-objective multi-area economic dispatch (MOMAED). Solution of MOMAED using distinct NI approach can found in ref [30-34].

Reserve requirement is an important issue by the stability and reliability point of view for the power system network. Several technical papers have used MAED with reserve based constraints [35-38].

In this paper Modified version of recently proposed salp swarm algorithm is proposed to solve complex constrained MAED, problems of power system. This paper is organized in the following manners. Section II gives the review of the related work on MAED problem. Section III is presenting formulation of problem, concept behind SSA and its modification in section IV, description of problem and simulation results are in section V and finally concluding remark is presented in section VI.

• II.    Literature Review

Pioneer wok for related to MAED problem includes [18-20]. In past NI techniques as harmony search

(HS)[21], artificial bee colony (ABC) [22], flower pollination algorithm (FPA)[23], evolutionary programming (EP)[24, 25], water wave optimization (WWO) [26], and teaching learning based optimization (TLBO)[27], were employed to solve MAED problems with different optional constraints. Attempt have been made for solution of two area problem with six generator unit system in ref [22],[23],[25-29], two area problem with four generator unit system in ref [29]. solution of MAED problem with three area system with three generator unit presented in ref [18] and with three area system with ten generator unit presented in ref.[22],[23],[25-30]. Whereas solution of MAED problem for four area with sixteen generating unit system are presented in [20, 21], [24], [29] and for four area forty generating unit system are presented in [22, 23], [25-29]. A comprehensive review of different metaheuristic and comparative analysis for solution of MAED problems are presented in ref [28].

Various solution approaches have been reported in literature that deal with solution of multi objective MAED problems using NI optimization. Solution of multi objective MAED problem with four area sixteen unit system found using ABC [29], chemical reaction optimization (CRO) in ref [30] and solution of four area forty unit system were presented using ABC [29], symbiotic organism search (SOS) [31], and using hybrid shuffle frog leaping algorithm and PSO in ref [32]. Hybrid direct search method (HDSM) were applied to solve reserve constrained two area six unit MAED problem [33], and variants of DE and PSO [35]. Hybrid DE and PSO presented in [34] to solve MAED problem in electricity market prospective using four area with sixteen generating unit system. Impact of wind penetration with three area 52 generating unit system is investigated in ref. [36] and with three area 54 generating unit system in ref [37-38].

• III.    Problem Formulation

MAED problem is basically extension of ED problem that knit together more area in a single network connected through tie-lines [18]. The objective function of MAED problem combines two terms: (a) fuel cost associated with committed power generating units in all area (b) cost associated with power exchange between interconnected areas [25, 29].

Considering quadratic cost function of committed generator unit, total fuel cost ( FC ) in all areas can be represented as [21, 22], [29]:

NM NM

FC X { X f j, ( P i, )} XX ( a ^ P + b . P i, + c , )} ⁽¹⁾ i = 1 j = 1 I = 1 j = 1

Here f ( P ) represents the fuel cost of j^th power generator in area i , a , b and c are the fuel cost coefficients, N is number of area and M represents the number of power generating unit in area i .

Active power transmission cost between areas ( TC ) can be represented as [22], [29]:

M - 1 M

TC = X X fA       (2)

j = 1 k = j + 1

f , Pt are the cost coefficient of power flow and power flow limit of tie line j to k respectively.

The objective function of MAED problem is to minimize the total costs F^Cost and also has to satisfy all operational constraints associated with it [20, 21].

Cost

" M

= X X MP) + TC

• A.    Area power balance constraints

In MAED problem the power balance constraints need to be satisfied for each area, neglecting transmission loss represented as [21, 22]:

M

XL Pi = Par + XLPtik , i ^e N        (4)

ij      di               ik j=1                   k, k * i

Where P is the power demand of i^th area, tie line power flow from i^th to k^th area is Pt .

• B.    Generating limit constraints

The real power output of each power generating unit must lie within their lower ( P ^min ) and upper ( P ^max ) limits, represented as [7-16], [22-29]:

Pmin < P, < P,max  i G N and j G M (5)

ij             ij        ij

• C.    Tie-line limit constraints

The tie-line real power flows ( T ) from area i to k area should be between the maximum ( T ^max ) and minimum ( — T max ) limits of tie-line flow and it is represented as [21-23]:

max            max

• — Tik   < Tik < Tik   .               (6)

• IV.    Salp Swarm Algorithm

  Salps are barrel shaped free floating tunicate belongs to family of salpida. They move forward in deep water by pumping their bodies by propulsion. Salps search their food source in Deep Ocean in the form of swarm called swarm chain. Based on unique swarming and foraging behavior salp swarm algorithm (SSA) for optimization is recently developed by Mirjalili in 2017 [39].

During optimization the possible solution of problem is considered as salp chain. The salp chain broadly classified in two groups i.e. leader and followers. Basically salp located at beginning of chain called leader whereas remaining salps are called followers. Best salp (best solution) represents food source which is followed by remaining salps. During iterative process leader salp changes their position according to food source and followers follows the leader without trapping to local optima finally converges to global optima solution in reasonable time frame.

x - x₀

t v final v0

With, v₀ = 0 the time in optimization process represents iteration and discrepancy between iteration considered as 1, analytically represented as (12):

Fig.1. Salp Chain

X j = 1( x j + X j ) i - 2

A. Modified salp swarm algorithm

Modification in SSA is applied to improve exploration and exploitation capability by avoiding stagnation of standard SSA. The exploration capability is enhanced by introducing more randomness. The random mutation is applied as below.

In the mathematical model salps are initialized randomly with ‘m’ dimension search space within lower and upper limits assuming ‘ F’ as food source (target).

Leader salp updates their position as (7):

j J Fj + c ( c₂ (Ubj - Lb_} ) + Lb_} ) X j  | F. - c ( c₂ (Ub. - Lb ) + Lb )

c 3 - 0.5   (7)

c ₃< 0.5

Where, X ¹ represents position of the first salp (leader) in the j^th dimension search space. F is the position of the food source in the   j^th dimension, Ub and

j

Lb represents the upper, lower bound of the j^th dimension respectively,

Eq. (7) shows that the leader only updates its position with respect to the food source.

The coefficient c 1 helps to make balance between exploration and exploitation and it is represented as (8):

c1

= 2 e

- (4 l )²

The parameter C and C are the random number between 0 and 1. Basically, they dictate whether the next position in j^th dimension should be towards positive infinity or negative infinity as well as the step size.

The position of follower salps updated with the help of Newton’s law of motion (9):

1     0

i 2

x, = at + v,.t  i - 2

j ₂0

Here also salps are randomly initialized within lower and upper limit similar to SSA.

But in MSSA Leader salp updates their position as (13):

j  J Fj + c_x ( c₂ (Ubj - Lb_} ) + Lb_} )

X j  | Fj - c_x ( c₂ (Ubj - Lbj ) + Lbj )

c ₃ > 0.7

c ₃< 0.7

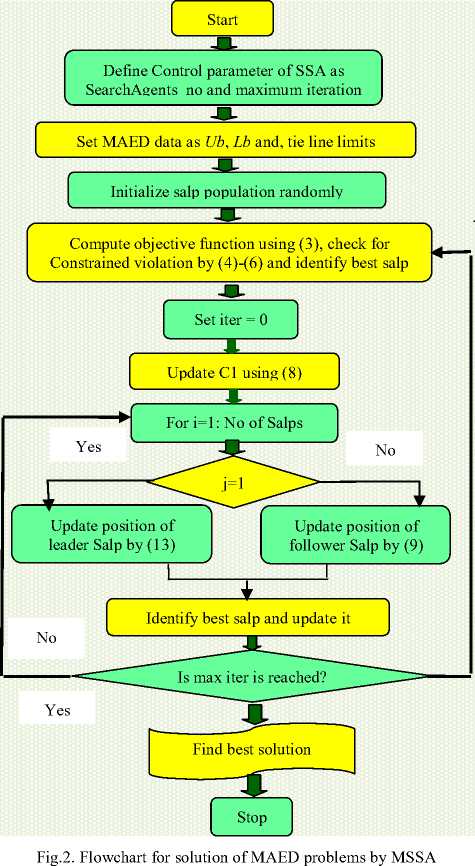
With C are the random number between (-1, 1) and C between (0, 1) . The solution procedure of modified SSA for solving MAED problems is depicted using flowchart in Fig. 2.

• V.    Results and Discussion

• 2.40GHz Intel core i3 processor with 4GB RAM. The description of test case and simulation results obtained by MSSA are presented as below. The search agent size for simulation is considered to be 100.

Performance of MSSA is evaluated on two types of problems. First type of problem consists of standard mathematical benchmark functions and second type of problem is related with power system scheduling with three different test cases of single and multi area ED problem with different complexity level. MSSA have been implemented in MATLAB 13 and executed on

• A. Test case 1

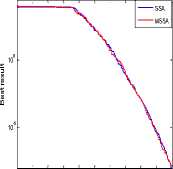
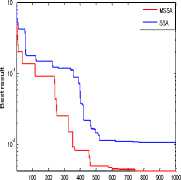
It has standard mathematical benchmark functions comprise with unimodal, multimodal and composite modal. The descriptions of function and dimension of test cases along with its upper and lower limits considered for simulation analysis are presented in Table 1. Simulation analysis was carried out on these functions using MSSA over thirty repeated run considering large dimension. The outcomes of simulation results in terms of statistical parameter are tabulated in Table 2. The comparison of convergence characteristics of SSA and MSSA for all tested benchmark under consideration is also plotted in Fig.3 (a) to Fig.3 (e).

Statistical results and convergence curves listed below. It is clear that MSSA performs better as compared to SSA, PSO and GA.

• Table 1. Description of benchmark test functions

Function (Dimension =30)

К = 2 L xi , — 100 ⁵ x. ^{5 100} &  f min = 0

f 2 = 221 Х + П21 x |, - 10 5 x. 5 10, f mn = 0

f = 2 mU x 4 + random (0,1), - 1.28 5 x . 5 1.28, f min = 0

• - 0.02 m " ' £ x ²     m - 2 „(2„ , )

f 4 =- 20 e   '  “  - e -      + 20 + e ; - 32 5 x 5 32 , f min = 0

f = 0.1[sin² (3 nx ) + 2 m ( x - 1) 2 {1 + sin² (3 nx + 1) + ( x„ - 1)²{1 + sin² (2 nx _n)} }] + 2 m u ( x ,5,100,4)

• - 50 5 x . 5 50, f „n = 0

  

  Fig.3(a). Sphere function

  
  
  

  100  200   300  400   500  600  700  800  900  1000

  Iteration

  
  
  
  
  
  

  -50                      _-50

  
  
  
  
  
  
  
  
  

  Fig.3(b). Schwefel function

  
  

Table 2. Simulation results of benchmark functions

f		f 1	f 2	f 3	f 4	f 5
MSSA	Ave	1.2235e-08	7.8202e-06	0.00202	9.7746e-06	5.9602e-11
	Std	1.8387e-09	1.2522e-06	0.0025	2.2038e-06	2.8124e-11
SSA[40]	Ave	0.000	0.2220	0.0028	0.0598	0.000
	Std	0.000	1.000	0.0070	0.5279	0.000
PSO[40]	Ave	0.2148	0.2858	0.0817	0.5917	0.0962
	Std	0.2663	0.0867	0.0635	0.9783	0.0911
GA[40]	Ave	0.3485	0.4172	0.3625	0.8864	0.0335
	Std	0.3714	0.0762	0.1503	0.2961	0.0438

Iteration

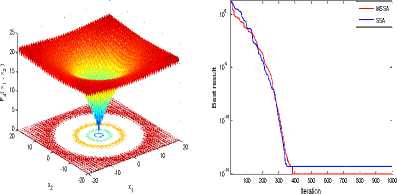
Fig.3(d). Ackley function

Fig.3(c). Quartic function

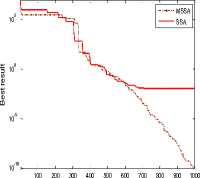
Fig.3(e). Levi function

Fig.3. Benchmark functions and their convergence curve

• B.    Test case 2 (a)

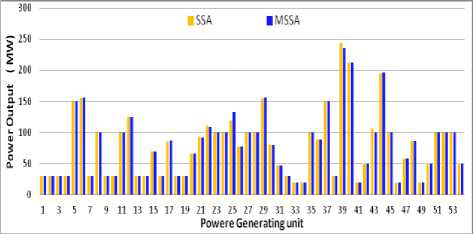
Fig.4. Optimum generation scheduling for 54 thermal unit system

Table 3. Comparison of simulation results for Test case 2 (a)

Method	Generation Cost ( $/ hr )
	Min Cost	Average Cost	Worst Cost
FPA[16]	22,432.3804	22,483.1643	22,896.9444
MFPA[16]	22,432.2307	22,432.2801	22,432.9153
SSA	22449.1679	22541.52722	22592.7308
MSSA	22432.2447	22446.9487	22495.6752

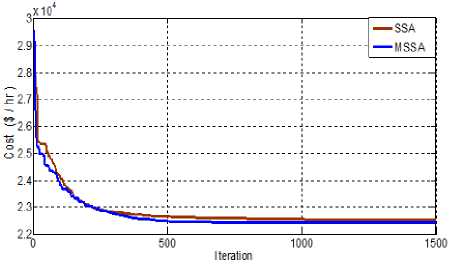
Fig.5. Convergence curve of SSA and MSSA for Test case 2(a)

• C.    Test case 2 (b)

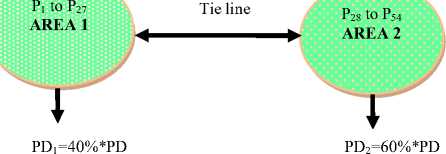
Fig.6. Two-area network with fifty four generating units

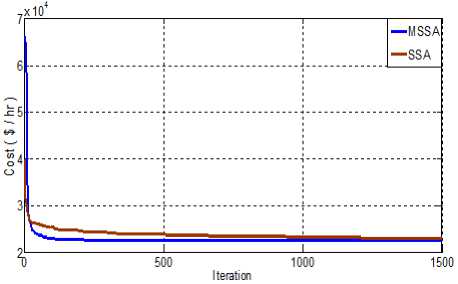
Fig.7. Convergence curve of SSA and MSSA for Test case 2 (b)

Table 4. Optimum generation scheduling for two area network Test case 2 (b)

AREA1 (PD 1 =40% *PD)			AREA2 (PD 2 =60% *PD)
unit	SSA	MSSA	unit	SSA	MSSA
P 1,1	29.6289	30	P 2,1	100	100
P 1,2	29.9746	30	P 2,2	183.2269	172.5939
P 1,3	29.3312	30	P 2,3	83.5606	84.2442
P 1,4	29.6695	30	P 2,4	49.3162	50.8741
P 1,5	152.1105	150	P 2,5	29.9581	30
P 1,6	135.4819	135.3002	P 2,6	19.6857	20
P 1,7	29.8818	30	P 2,7	19.7627	20
P 1,8	93.7774	99.9976	P 2,8	98.4046	100
P 1,9	29.8915	30	P 2,9	95.7134	96.5487
P 1,10	29.3854	30	P 2,10	150	150
P 1,11	100	100	P 2,11	29.9546	30
P 1,12	109.864	107.5305	P 2,12	256.4547	253.9666
P 1,13	29.5269	30	P 2,13	238.0034	231.3157
P 1,14	29.5576	30	P 2,14	19.9958	20
P 1,15	62.5678	62.0927	P 2,15	49.8045	50
P 1,16	29.4705	30	P 2,16	100.1254	100.0001
P 1,17	75.5007	74.9378	P 2,17	221.8563	215.2065
P 1,18	29.6521	30	P 2,18	100.0002	100
P 1,19	29.6448	30	P 2,19	19.8437	20
P 1,20	58.67	59.7689	P 2,20	56.5628	64.9687
P 1,21	79.0068	83.9322	P 2,21	93.6883	96.0421
P 1,22	106.0561	96.863	P 2,22	19.3746	20
P 1,23	99.2221	100	P 2,23	49.6174	50
P 1,24	99.8019	96.0321	P 2,24	84.4825	100
P 1,25	129.6249	120.8426	P 2,25	99.3574	100
P 1,26	66.7492	68.9418	P 2,26	99.9372	100
P 1,27	99.3111	100	P 2,27	49.9538	50
T 12				126.5592	119.4394
Cost ( $ / hr )				22660.1069	22605.891931

• D.    Test case 2(c)

It is much complex test case with three area networks. The cost coefficient data and total load demand are similar to case 2(a). Here fifty four generating units are segregated in three areas having each area of eighteen units. Each area shares the power demand of 20% in area one, 30% in area two, 50% in area three respectively. The whole network topology considered in this case is shown below in Fig.8. Here also power flow limit between each area are considered as 200 MW similar to test case 2 (b). With search agent size 100 over 1500 iteration, the simulation results in terms of optimum generation scheduling obtained by MSSA and SSA is listed in Table 5 and their convergence curves are presented in Fig. 9. Here also it is clearly observed that MSSA performs better for competitively large scale complex constrained test system.

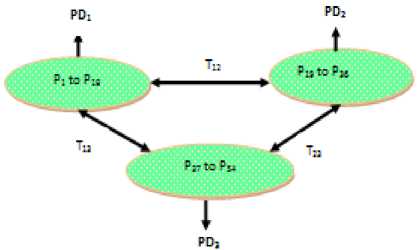
Fig.8. Three area topology with fifty four generating units

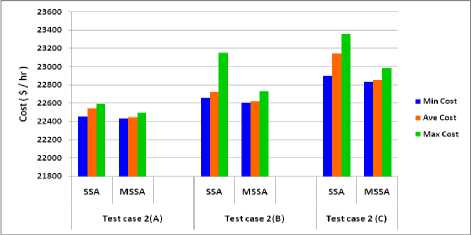
Fig.10. Comparison of Cost for practical Test cases

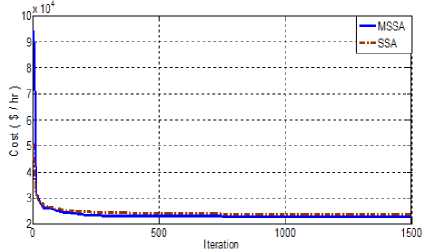
Fig.9. Convergence curve of SSA and MSSA for Test case 2 (c)

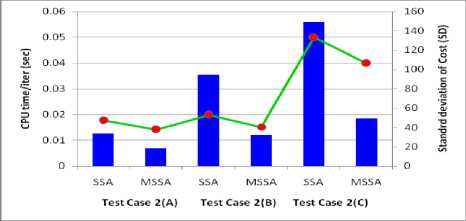
Fig.11. Comparison of Standard deviation and CPU time

• E.    Statistical Analysis of results

Simulation analysis has been carried out over 30 repeated run with search agent size of 100 for each test case. For test case 1, having mathematical benchmarks with diverse nature, the statistical comparison of results are made in Table 2 with other methods. Here, it is clearly observed that MSSA performs better than SSA, PSO and GA with low standard deviation (S.D.) for almost all tested benchmarks. Also for practical constrained optimization problems listed as Test case 2(A) to 2(C), simulation results over 30 repeated run with search agent size of 100, Comparison of statistical results in terms of minimum cost, average cost and maximum cost obtained by SSA and MSSA is presented in Figure.10. Standard deviation (S.D.) and average computation time (second) considered by two computational methods for practical test cases are presented in Fig. 11.Here also it is clearly observed that MSSA attained minima with low SD and CPU time in all tested problems in consistent manner. It may be due to increase in diversification and avoidance of local minima during optimization.

• VI. Conclusion

In this paper modified Salp Swarm algorithm (MSSA) is proposed for solution of constrained optimization problems. Salps are basically marine organisms. They form long dense swarm during their foraging headed by leader salp. Salps updates their position based on position of leader and followers depending on availability of food source. Salp swarm algorithm (SSA) basically a nature inspired optimization approach that mimics the unique swarming and foraging behavior of salps in its analytical model that comprises of stochastic initialization, fitness calculation and updation similar to other NI optimization. In MSSA modification has been carried out in updation phase by introducing more randomness, which helps to strengthen the exploration and exploitation property of SSA and enhance the searching capability in better manner. MSSA and SSA is implemented and tested on two types of problems, type one is related with five mathematical benchmarks with different distinct nature and type two has three complex constrained optimization problems related to power system scheduling problems. To validate the simulation results comparison are also made with results available in recent literatures .Considering all simulation results obtained by SSA and MSSA we can say that MSSA has potential to offer superior solution with reasonable CPU time and it can be applied to solve other real world problem in efficient manner.

Table 5. Optimum generation scheduling for three area network Test case 2(c)

AREA1 (PD 1 =20% *PD)			AREA1 (PD 1 =30% *PD)			AREA1 (PD 1 =50% *PD)
unit	SSA	MSSA	unit	SSA	MSSA	unit	SSA	MSSA
P 1,1	28.4067	30	P 2,1	29.1216	30	P 3,1	150.0018	150
P 1,2	24.9844	30	P 2,2	63.8576	62.6835	P 3,2	29.9202	30
P 1,3	25.3081	30	P 2,3	98.3576	87.5147	P 3,3	263.6299	263.1022
P 1,4	23.3214	30	P 2,4	114.8067	101.9755	P 3,4	247.4829	240.7523
P 1,5	153.2199	150	P 2,5	98.9125	100	P 3,5	19.9992	20
P 1,6	151.2317	132.7213	P 2,6	99.9593	100	P 3,6	49.7924	50
P 1,7	29.999	30	P 2,7	121.3953	125.9702	P 3,7	111.114	100
P 1,8	93.1698	95.3609	P 2,8	71.2182	72.4465	P 3,8	246.5447	225.2442
P 1,9	29.6561	30	P 2,9	99.9157	100	P 3,9	100.0528	100
P 1,10	28.7963	30	P 2,10	100.2046	100	P 3,10	19.9943	20
P 1,11	100.0033	100	P 2,11	138.2129	147.6164	P 3,11	66.1769	69.1804
P 1,12	126.2681	104.3482	P 2,12	87.22	80	P 3,12	85.2793	100
P 1,13	9.4604	30	P 2,13	36.6612	43.6419	P 3,13	19.996	20
P 1,14	29.7881	30	P 2,14	29.9935	30	P 3,14	48.1012	50
P 1,15	52.0936	61.2984	P 2,15	15.1111	20	P 3,15	99.9801	100
P 1,16	28.6801	30	P 2,16	19.9996	20	P 3,16	99.9063	100
P 1,17	83.8162	74.6712	P 2,17	99.9828	100	P 3,17	99.9998	100
P 1,18	29.842	30	P 2,18	64.995	83.4722	P 3,18	46.0578	50
T 12							0.0012	0.0000
T 13							199.644	200
T 23							117.3264	132.7209
Cost ($/hr)							23045.5133	22831.5761