Single Channel Speech Separation Using an Efficient Model-based Method

Published Online February 2015 in MECS

Speech signals are seldom available in pure form for speech processing applications, and are often corrupted by acoustic interference like background noise, distortion, simultaneous speech from another speaker etc. In such scenarios, it becomes necessary to first separate the speech from the background. In particular, the task of separating overlapping speech from multiple speakers, called speech separation, is especially challenging since it involves separating signals having very similar statistic and acoustic characteristics. The separation problem has attracted immense research effort in the past two decades, more so for the case when the mixture is available only from a single channel and multi-channel approaches cannot be used. This single channel situation is called the single channel speech separation problem and the two speaker case can be formulated as z(t) = x(t) +y(t), where x(t) is the speech signal of speaker one and y(t) is the speech signal of speaker two. Many techniques have been proposed to solve this problem. These approaches are mainly divided into two categories: source driven [1-4] and model-based methods [9-15].

As a major example for the first group, computational auditory scene analysis (CASA) has widely been studied [1]. Generally speaking, CASA-based methods aim at segregating audio sources based on possible intrinsic perceptual acoustic cues from speech signals [2]. For

CASA systems, a reliable multi-pitch tracking component is critical to find pitch trajectories of two interfering speech signals [5]. The CASA methods are fast and could be implemented in real time. There are, however, challenges that limit the pitch tracking performance for a mixture [2]: (1) Most existing pitch estimation methods perform reliably only with clean speech signals that have a single pitch track or harmonically related sinusoids [6] with almost no background interference [7]. (2) It is possible to perform a reliable pitch estimation using a mixture of a dominant (target) and a weaker (masking) signal as long as the pitches of the masking and target speech are different in a short frame [3]. A high similarity between the interference and target pitch trajectories results in performance degradation of CASA methods [8]. (3) Because of energetic masking defined in [8], the weaker signal frames are masked by the stronger ones complicating the pitch estimation. Accordingly, at targetdominant time-segments, it is possible to accurately track the pitch contour of only the dominant (target) signal. (4) Pitch tracking performance has not been promising for scenarios where the underlying signals include mixtures of unvoiced and voiced frames and as a result, the separated speech signals include severe cross-talks [4].

Model-based single channel speech separation is commonly referred to as the techniques which use the trained models of the individual speakers to separate the sources from a single recording of their additive mixture. The most prominent models are vector quantization (VQ) [9], [13], Gaussian mixture models (GMM) [11], [12] and Hidden Marcov models (HMM) [14]. Given the individual speakers' models, an estimation technique is applied to estimate the sources. In most recent proposed model-based single channel speech separation techniques, it is assumed that the test speech files are recorded at a condition similar to that of the training phase recording. This assumption is not, however, realistic and highly limits the usefulness of these techniques. Therefore, it is of great importance to consider situations in which the test speech files are mixed at an energy ratio different from that of the training speech files. In these situations, a desired technique is one that first estimates the gains associated with the individual speakers.

In [15], a technique is proposed in which, it is shown that gains of the speech signals can be expressed in terms of a signal-to-signal ratio (SSR) and using this relation a gain adapted minimum mean square error (MMSE) estimator is derived to estimate the sources. Following that, the patterns of the speakers and SSR which best model the observed signal in an MMSE sense are obtained. However this method sounds efficient to gain estimation, but it results long time processing in practice. In our proposed method we take the superiority of VQ which is simplicity computation to separate the speech signals [13]. In this paper we introduce sub-section VQ and use it instead of conventional VQ to achieve high accuracy in estimating gains and speech signals.

The rest of this paper is organized as follows. In section II, preliminary definitions are described where we express the sources-observation relation in the feature space and also the relation between speakers’ gains and energies of the underlying signals. In section III, we give a description of training phase. In this section we introduce sub-section VQ method and show how it is applied in separation process. In section IV, details are given on how the gains of the speakers are estimated and how the estimated gains are applied to estimate the sources. Experimental results are reported in section V where the proposed technique is compared with a gain adapted MMSE estimator [15]. Finally, conclusions are given in section VI.

• II.    Preliminary Definitions

• A.    Gain-SSR Relation

In gain adapted methods, the relation between observation signal and the two sources is supposed to be

L—1

/ j2nd\ v-1 j2nld X(e L )=∑Х(l)e L d=0,1,…,D-1

Let X denote the D dimensional, log spectral vector (feature vector) with dth component, X(d), defined by

X(d) = log10 |X(e j2nd /L)|  d=0,1,…,D-1     (5)

The relations between x[l], |X(e j2nd ^/L)|, ∠ Х(ej2nd ^/L) and X(d) are shown in Fig. 1.

{ X ( I )} 1 = 0

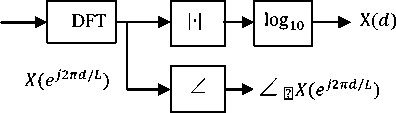
Fig. 1. Feature extraction

Let xr and y r be the L-dimensional vectors of the rth frames for the speech signals of speaker one and two in the time domain, respectively and z r be the corresponding frame of the observation signal. We next form the following vectors as the feature vectors according to Fig. 1

Xr =log10(|FD (x Г)|)

YГ =log10(|FD (y Г)|)

ZГ =log10(|FD (z Г)|)

z(t) =g x(t) +gуy(t)   t=0,1,…,Т-1     (1)

where g and g у , which are positive parameters, are speakers’ gains and it’s supposed that these speech signals have equal power before gain scaling, G ₌

∑tx2(t)= ∑ty2(t) . In [15] the speakers’ gains are obtained in terms of SSR (signal to signal ratio), square root of power of the observation signal and GО

g

g

and

G0√1+10 10

gу

g

G0√1+1010

where gI=  ∑tz2 (t) is power of the observation

„2

signal and SSR=10log10   . Also, a and aу are defined gy as a =log10 g and a у=log10 gу         (3)

where X r, Yr , and Z r denote the D -dimensional log spectral vectors of speaker one, speaker two, and the mixed signal, FQ (∙) denotes the D-point discrete Fourier transform, and |∙| denotes the magnitude operator.

The relation between feature vectors of the observation signal and the sources can be obtained using MIXMAX approximation [16]

Ẑ r = MIXMAX(Xr+a ,Yr+aу) = [max(Xr(1)+ a ,Yr(1)+aу),…,max(Xr(d)+a ,Yr(d)+      (9)

aу) ,…,max(Xr(D)+a,Yr(D)+aу)] T

This relation is used in the separation process to estimate the sources.

which will be used in gain estimation and source estimation process.

B. Sources-Observation Relation

Log magnitude of discrete furrier transform was selected as our feature. Let x(l) l=0,1,…,L-1 be the samples of some speech signal segment (frame), possibly weighted by some window function, and let X(e j2nd /L) denote the corresponding short time furrier transform.

• III.    Modeling the Sources

• A. VQ Modeling

VQ is referred to the techniques in which a set of available data vectors Ф={φm}, m=1,2,…,M are partitioned into a number of clusters Vn,n=1,2,…,N such that Ф=⋃n=l V „ and ⋂ n=l Vn=∅. Every cluster Vn is represented by a vector called a codevector cn and the set of all codevectors is called a codebook C={cn, n=1,2,…,N}. In this paper we use LBG algorithm for VQ [17]. In this algorithm, clustering is performed in a way two optimality criteria which are:

nearest neighbor condition

V П ={φ m :‖φ m -сn‖2<‖φ m -сn' ‖2, n≠n}  (10)

and centroid condition

∑Фт ∈Vn φт сn=∑     1

^Фт ∈  1

n=1,2,…,N       (11)

are met. In VQ modeling, a codebook is obtained for every speaker using training feature vectors of that speaker.

B. Sub-section VQ Modeling

In this method, training log spectral vectors for each speaker are divided into four sub-sections and for every sub-section, a VQ model is obtained. Also, log spectral vector of observation ( Z Г ) is divided into four subsections such that Z Г=[Z[;Z2;Z3;Z4 ] . We assume Xr=[X[;X ;X ;X4 ] and Y Г=[Yf;Y2Г;Y3r;YI] in which, Xк,k=1,2,3,4 is the kth sub-section vector of Xr and also, Y£,k=1,2,3,4 is the kth sub-section vector of Yr. According to (9) we have

Ẑ £ = MIXMAX(X +a ,Y £ +a у )  k=1,2,3,4   (12)

Sub-section VQ models are used to estimate the gains and the sources.

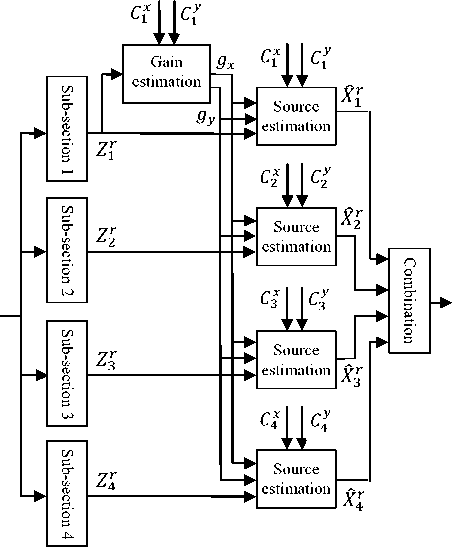
Fig. 2. Schematic of our proposed gain adapted single channel speech separation system

• IV. Estimating the Sources

The single channel speech separation presented in this paper involves three stages. In the first stage, the speakers' gains are estimated. In the second stage, the estimated gains of the speakers are used to estimate the sub-section feature vectors of each speaker and in the third stage, time domain signal of each speaker is obtained from feature vectors of the associated speaker. Fig. 2 illustrates our proposed gain adapted single channel speech separation method. As the figure shows, Zr indicates the feature vector of the observation signal, Cк ,k=1,2,3,4 is the codebook of speaker x in the kth sub-section, Cк , k=1,2,3,4 is the codebook of speaker y in the kth sub-section and ̂X is estimated feature vector of speaker x.

• A. Gain Estimation

As the Fig. 2 shows, the gains of the speakers are estimated in the first sub-section. In order to estimate the gains, we estimate the SSR. For a given SSR, a and aу are obtained using (2) and (3). Let с̃ , be MIXMAX estimator of two arbitrary codevectors in the first subsection, that is, с̃ , =MIXMAX.сJ. +a ,с [ +aу/ (13)

where с^. and с у are two arbitrary codevectors of speaker x and speaker y, respectively. All pairs of codevectors {с^. ,с у } are compared to find the minimum mean square error (MMSE) compared to the observation signal's feature vector Z[ . SSR which minimizes the MMSE for all frames is selected as the estimated SSR

SSR ^∗ =argmin SSR

∑ r m,in(∑ d (Z : (d)

-

с̃ , (d)))

We     define    Q(SSR) = ∑_r min , (∑ d (Z[(d)-

с̃ , (d))). Unlike the Q(SSR) defined in [15], it can be shown that our proposed Q(SSR) is a convex function.

Here we give a brief description to prove it: using (13), (3) and (2), Z[(d) -с̃ , (d) can be written as

Z[(d) -max(сlj(d) +log10 .г/- log10(1+ \  1               xuo/ 2\

-SSR\                 /а \           /SSR\\

10   ),сГ,(d) +log10 . £/- log10(1+10))

Both - log10(1+10   ) and

- log10(1+

SSR \

10  ) are concave functions. So, both functions in max

function argument are concave functions. Max of two concave functions is a concave function and when it’s

multiplied by a negative number, it becomes convex. So, Z [ (d) -с̃ , (d) is a convex function. Since power two of a convex ^, function, summation of a number of convex functions and min of a number of convex functions are all

convex

∑r min i ,j

functions,

(∑ d (Z [ (d)

-

we deduce that  Q(SSR) =

с̃ , (d)))

is a convex function.

More information about convex functions can be found in

As we proved above, Q(SSR) is a convex function, so it has a global minimum, mathematically Q(SSR ^∗ ) <  Q (SSR), ∀ SSR≠SSR ^∗ . To find SSR ^∗ , we can use a very efficient iterative quadratic optimization algorithm presented in [19] and used in [15]. In this algorithm, three points are selected

{(SSR , Q(SSR )),(SSRс, Q(SSRс)),(SSRг, Q(SSRг))} and they are updated each iteration to obtain a quadratic function of the form f(x) =ax2 +bx+с . Update of the points is performed usingx∗=- , the value that minimizes f(x), and Q(x∗). For initialization we regard: SSR ←SSRmin, SSRг←SSRmax, and SSRс← an arbitrary value between SSRmin and SSRmax . The algorithm iterates until reaching a value of SSRс that Q(SSR ) ≥Q(SSRс) ≤Q(SSRг). In experiments, we can see that for SSR>18 dB the signal with higher energy which is called target signal, completely masks the signal with lower energy known as interference signal. So we can set SSRmin =0 dB and SSRmax=18 dB. Now, using the estimated SSR (SSR∗) we obtain the estimated gains of the sources (g∗ and g∗) from (2). The estimated gains are used in the next subsection to estimate the feature vectors.

• B.    Source Estimation

Using the estimated gains of the sources, we obtain a∗ and a∗ from (3) and use them to form the MIXMAX estimator of two arbitrary codevectors of the speaker one and speaker two in the kth sub-section с̃ , =MIXMAX.сki +a∗,с £ +a∗/        (15)

Then in each sub-section, for each frame we select the optimal codevectors that cause minimum mean square error (MMSE) between the feature vector of the observation signal and the MIXMAX estimator

{i ^∗ ,ј ^∗ }=argmin ^,j

(∑ _d (Z к(d) -с̃к™ , Г(d)))

Then, we use a simple soft mask filter to estimate log spectral vectors of speaker x and speaker y . In this method, the dth component of the estimated log spectral vector in the kth sub-section for speaker x is given by

̂X £ (d)

Z£(d)- a ^∗ ={_с ki ∗ (d)

^с ki _∗ (d)+a ^∗ >сkj _∗ (d)+a ^∗ с ki _∗ (d)+a ^∗ <сkj _∗ (d)+a ^∗

Similarly, the estimation of Y£ (d) is given by

̂Y £ (d)

Zк(d) -a∗    ск,∗(d)+a∗>сki∗(d)+a∗ сkg∗(d)        с kj∗(d)+a∗<сki∗(d)+a∗

Then, the estimated sub-section vectors of each speaker are combined to obtain the entire feature vector of each speaker,   X̂r=[X̂ [ ;̂X ;X̂ ;̂X4 ]   , Ŷ =

[Ŷ Г;ŶI;ŶJ;̂Y4].

• C.    Synthesizing Estimated Speech Signals

Here, the reverse of what we do for feature extraction is applied to the estimated log spectral vectors of each speaker to obtain time domain signals:

The estimated log spectral vectors of each frame (X̂r and Ŷ r ) are transformed to the spectral domain and combined with the phase of the observed signal. Then, a D-point inverse DFT is applied to transform the vectors to the time domain. Mathematically, the procedure is expressed by x̂ r=FD1 (10 ̂ exp [(-1)2∠FD (z Г)])     (19)

and ŷ Г=FБ1 (10 ̂ exp [(-1)2∠FD (z Г)])     (20)

where ∠ 13 denotes the phase operator, exp[∙] denotes the exponential function, and FQ¹(∙) represents the D-point inverse Furrier transform and x̂ and ŷ are the estimated frames of signals in the time domain. Finally the inverse transformed vectors are multiplied by a Hann window and then the overlap-add method is used to recover the sources in the time domain.

• V.    Experimental Results

Our proposed method is evaluated in this section and it’s compared with the method presented in [15] which is a gain adapted MMSE estimator. The database we use for our experiments is presented in [20]. In our experiments, the sampling rate of the signals is decreased to 8 kHz from the original 25 kHz. In the test phase, to obtain mixed signals with different SSRs we select 10 pairs of speech files randomly that are not used in the training phase and mix them at SSRs equal to 0, 6, 12 and 18 dB. In the mixed signal, the speech signal that has higher gain is the target signal and the signal with lower gain is the interference signal. In both training and test phases, frames of the speech files are obtained using a hamming window whose length is 50 ms and it’s frame shift equals 20 ms. In the phase of reconstructing separated speech files, a Hann window is used in overlap add method. To obtain feature vectors of them, a 512 point discrete furrier transform is applied to them and after taking log magnitude of them and discarding their symmetric portions, 257 dimensional feature vectors are obtained. Afterward, we select 128 codevectors as the size of the codebook. In order to generate sub-section VQ models, training feature vectors of each speaker are divided into 4 sub-sections, 65-point log spectral vectors for first subsection and 64-point log spectral vectors for other subsections, and a VQ model is obtained for every subsection.

The similarity between the original signal and the estimated signal of speaker x is measured by signal-to-noise ratio (SNR) which is defined as follows

∑t(x(t))2    1

SNR =10log10 *∑ ;(x(t)-x̂(t)) 5 +         (21)

where x(t) and x̂(t) are the original and estimated speech signals respectively.

Our experiments include two stages: in the first stage, in order to show the effectiveness of our proposed VQ based gain estimation approach in the first sub-section, we select 20 pairs of speech files randomly and mix them at random integer SSRs within the interval [0, 18] dB. Then we estimate the SSR for each mixture using (14) and compare it with the actual SSR. We also keep tracking of the number of iterations performed in the quadratic optimization algorithm to reach estimated SSR ( SSR ^∗ ). Our experimental results of this stage are presented in Table 1. This table includes 4 columns. The first column determines the number of the mixture. The second column gives us the actual SSR of the corresponding mixture. The third column gives us the estimated SSR of the corresponding mixture and the forth column reports the number of iterations at which the quadratic optimization algorithm is reached to the corresponding estimated SSR. As it can be seen from the table, our proposed gain estimation approach estimates the SSR with reasonable accuracy and these estimated SSRs are reached with only one or two iterations for most of the cases.

Table 1. Experimental results of our proposed gain estimation method performed on 20 randomly selected pairs of speech files and mixed at random integer SSRs within interval [0, 18] dB

mixture	SSR actual	SSR∗	Itr
1	7	6.0204	1
2	12	11.0332	3
3	5	5.6115	1
4	1	1.5112	1
5	10	8.7727	2
6	9	8.5915	1
7	6	7.5366	2
8	2	2.2444	1
9	15	15.1206	2
10	4	3.4199	1
11	8	7.8029	2
12	13	12.5192	1
13	17	16.4497	1
14	2	2.8750	2
15	11	11.9618	3
16	5	4.4533	1
17	3	4.0130	1
18	9	8.1751	1
19	14	12.2161	3
20	7	5.8547	1

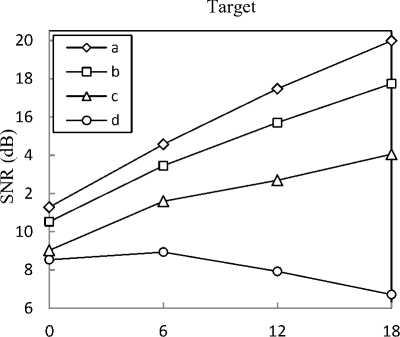
In the second stage of our experiments, we try to show the effectiveness of the entire gain adapted single channel speech separation system we proposed. For this purpose, we select 10 pairs of speech files randomly that are not included in the training phase and mix them at SSRs equal to 0, 6, 12 and 18 dB. Fig. 3 and Fig. 4 show averaged SNR results versus SSR for separated target and interference speech signals respectively, for: our proposed method (◊ line), the method presented in [15] which is a gain adapted MMSE estimator (□ line), our proposed method without gain adaptation (Δ line), and MMSE estimator (ο line). As the figures show, our proposed method outperforms the gain adapted MMSE estimator for both target and interference signals and also it can obviously be seen that when gain estimation is not included in that methods, separation performance greatly degrades which signifies importance of gain estimation in model-based methods. Our proposed method has much lower computational complexity with respect to gain adapted MMSE estimator, because both gain estimation and source estimation phases in our method deal with fewer parameters.

SSR (dB)

Fig. 3. averaged SNR versus SSR for separated target speech files obtained from our proposed method (a), gain adapted MMSE estimator (b), our proposed method without gain estimation (c) and MMSE estimator (d

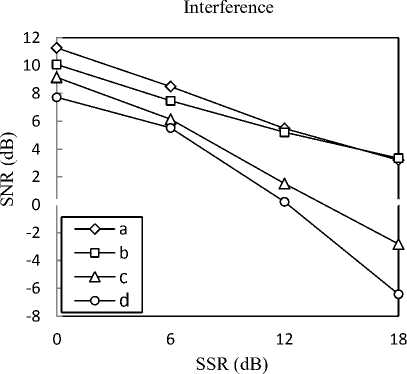
Fig. 4. averaged SNR versus SSR for separated interference speech files obtained from our proposed method (a), gain adapted MMSE estimator (b), our proposed method without gain estimation (c) and MMSE estimator (d)

• VI.    Conclusions

Gain difference between speakers causes improper performance of model-based single channel speech separation methods. In this paper we proposed a new VQ-based method to compensate this difference. In our proposed method, separation process is performed at the sub-section levels, gains of the speakers are estimated in the first sub-section and the estimated gains are used to estimate the feature vectors of the speakers in each subsection. Experimental results show that our proposed method outperforms the gain adapted MMSE estimator presented in [15].