Сингулярный элемент графовой модели упругой среды в декартовой системе координат

Анализ напряженно-деформированного состояния около дефектов типа трещин в деформируемом твердом теле составляет одну из основных проблем механики разрушения. При этом, как правило, распределение напряжений и деформаций в окрестности вершины трещины обладает особенностью типа r ^-а , где r — расстояние от исследуемой точки до кончика трещины.

Асимптотика r 0 5 присуща чисто упругим решениям [1, 2], а случай 0,5 <а< 1 возникает при решении нелинейных или упругопластических задач [3–5], а также в тех задачах, где трещина выходит на границу раздела двух сред с различными упругими свойствами [5, 6].

Следует отметить высокую чувствительность численных методов к особенностям моделирования напряженного состояния вблизи особых точек. В связи с этим предложен ряд альтернативных подходов к построению сингулярных конечных элементов, и в настоящее время парк этих элементов достаточно широк [7, 8]. Анализ результатов многочисленных исследований позволяет сделать вывод о том, что точность решения задач механики разрушения существенно повышается при адекватном моделировании асимптотики параметров напряженно-деформированного состояния у вершины трещины. Более того, в традиционных численных методах качество аппроксимации подчас важнее, чем количество используемых элементов и расположение узлов.

При численном решении разнообразных задач механики сплошной среды (и механики разрушения в частности) основными достаточно эффективными и широко

распространенными являются метод конечных элементов и метод граничных элементов. Общей закономерностью этих методов является то, что на этапе моделирования подвергается дискретизации не сама среда, а её континуальная модель. В то же время представляется целесообразным применение дискретных подходов на более ранних этапах моделирования. Такие возможности открывает метод анализа полей деформаций и напряжений, использующий в качестве дискретных моделей сплошного тела ориентированные графы [9–11]. Анализ системы на основе графового подхода сводится к тому, что: 1) среда делится на части, имеющие известное математическое описание (в рассматриваемом ниже случае — закон Гука); 2) для каждой части строится подграф (элементарная ячейка), являющийся ее моделью; 3) элементарные ячейки объединяются в граф — модель анализируемого тела, после чего с помощью матриц, характеризующих структуру графа, и уравнений, описывающих элементарные ячейки, получаются уравнения для системы в целом.

В основе вывода определяющей системы уравнений лежат вершинный и контурный законы Кирхгофа. Известно, что граф является моделью физической или технической системы только в том случае, если выбранные при его конструировании переменные удовлетворяют вершинному и контурному законам. Эти законы были установлены Кирхгофом для электрических цепей применительно к токам и напряжениям. Впоследствии оказалось, что они носят фундаментальный характер и применимы ко всем переменным вне зависимости от их физической природы [12]. Согласно вершинному закону алгебраическая сумма последовательных переменных, представленных дугами графа, равна нулю, а в соответствии с контурным законом алгебраическая сумма параллельных переменных равна нулю на любом замкнутом контуре.

Важно отметить, что континуальную модель сплошной среды удается полностью восстановить из ее дискретной модели в виде ориентированного графа. Можно показать [9–11], что при уменьшении размеров сетки вершинный и контурный законы приводят к выполнению уравнений равновесия и совместности деформаций теории упругости, что влечет сходимость приближенного решения к точному.

Данная работа посвящена построению на основе графовой модели сингулярного элемента, предназначенного для расчета напряженно-деформированного состояния в окрестности особых точек разреза, вблизи остроконечных включений и других сингулярных точек и линий двумерной упругой среды.

2.    Конструирование элементарной ячейки

Основой для построения моделей в виде графов служит объективный характер операций измерения выбранных независимых переменных. Как известно, целью любого измерения является установление зависимости между значением переменной и показаниями прибора. В то же время измерение связано как с точками системы, между которыми оно осуществляется, так и ориентацией измерителя. Эти свойства операции измерения можно представить направленным отрезком, то есть дугой графа.

С точки зрения операции измерения все переменные вне зависимости от их физической природы могут быть подразделены на два типа — параллельные и последовательные [12]. Параллельные переменные характерны тем, что измеритель подключается к двум точкам системы параллельно потоку энергии. Для измерения последовательных переменных прибор должен быть установлен в разрыв энергетического потока. К параллельным переменным относятся линейные и угловые разности перемещений, относительные скорости и ускорения, деформации, разности давлений, температур, электрических потенциалов и так далее. К последовательным переменным относятся силы, моменты сил, электрический ток, тепловой поток, поток жидкости или газа и другие. Выбор связной пары переменных определяется тем, что произведение последовательной и параллельной переменных должно давать скаляр с размерностью мощности или работы. При построении графа исследуемого тела за исходные удобно взять те переменные, которые измеряются установкой прибора непосредственно на исследуемый объект, то есть параллельные переменные.

Способ конструирования графа тела связан с процессом измерения полного и независимого комплекта переменных, которые однозначно характеризуют деформированное состояние элементов, полученных в результате декомпозиции. Элементарной ячейкой (графовым элементом) будем называть подграф, соответствующий одному элементу, полученному при разбиении исходной области на мелкие части.

При определении конфигурации элементарной ячейки в декартовой системе координат область, занятую двумерной сплошной средой, покрываем сеткой

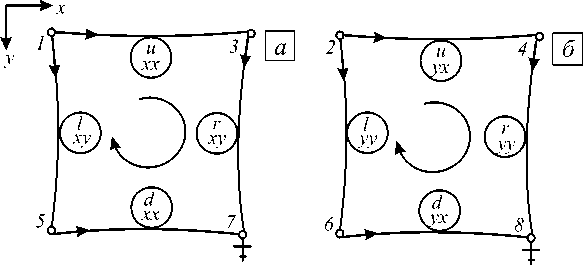
Рис. 1. Граф прямоугольного элемента сетки (в кружках – верхний и нижний индексы переменных, представленных дугами ячейки); u -компонента ( а ), υ -компонента ( б ); стрелкой показано направление обхода контура; точки 7 и 8 – корни подграфов

Измерители принимаем в качестве дуг графа и

координатных линий x = const, y = const, между узлами которой устанавливаем гипотетические измерители, определяющие абсолютные нормальные деформации 5 xx , 5 уу и деформации ⁵ y_X , ⁵ xy , обусловленные сдвигом. При этом 5 _xx измеряется между двумя точками оси x , 5 _xy — между двумя точками оси y , а 5 _yx — между двумя точками оси x и так далее.

изображаем их направленными отрезками линий, причем ориентация дуг совпадает с ориентацией осей координат. Точки, между которыми проводим измерения, считаем вершинами графа. Здесь подразумевается, что используются идеализированные приборы, то есть такие, что ножки нескольких из них могут быть одновременно установлены в одну и ту же точку тела. Поскольку одни и те же точки среды участвуют в разных группах измерений относительно осей x и y, то при построении графа они представляются разными вершинами. В результате получаем элементарную ячейку прямоугольного элемента, имеющую 8 дуг и 8 вершин и состоящую из двух компонент (Рис. 1).

Каждая из дуг графа отображает одну из следующих пар параллельных и последовательных переменных: ( 5xx , /xx ), ( 5yy , fy ), ( 5yx , fyx ), ( 5xy , fxy ), где fx , fyy и fyx , fxy — нормальные и тангенциальные внутренние силы (обобщенные напряжения). Таким образом, дугам элементарной ячейки соответствует следующая пара векторов:

{ f } T = { fix , / ", f x , /, ”' , fix , fi x' , / " , / ,'’ '} ,        { 8 } T = { 5 dx , 5 Уу , 5 dx , 5 Уу , 5 dx , 5 l„ , 5 u, , 5 ;, } ,    (1)

где индексы u, d, l, r обозначают, соответственно, верхние, нижние, левые и правые дуги элементарной ячейки, символ «Т» — операцию транспонирования, а индекс «c» указывает на принадлежность переменных отдельному графовому элементу.

Если измеряются положения точек тела относительно фиксированной системы

{ “ } .

координат, то в качестве параллельных переменных выступают перемещения { U } =

Для них парными последовательными переменными оказываются внешние силы, действующие на тело. При измерении перемещений ножки прибора устанавливаются между точкой тела и точкой пересечения нормали из нее с соответствующей осью координат. Этот тип дуги назовём внешним. В результате на каждой из осей декартовой системы координат появляется ряд точек, положение которых не зависит от деформирования тела. Это значит, что дуги, связывающие основания нормалей, нулевые, то есть их начальные и конечные вершины совпадают. Таким образом, все дуги, отображающие перемещения точек тела относительно фиксированных осей координат, имеют одну общую вершину в группе измерений по оси Ox и одну — в группе измерений по оси Oy. Поскольку некоторая определенным образом выделенная вершина в графе называется корнем [13], то указанные вершины и есть корни графового элемента.

3.    Построение матрицы жесткости сингулярного элемента

Связь элементарных векторов { f } c и { б } c , а также зависимость их от напряжений { σ } и деформаций { ε } упругого тела устанавливаем, принимая в качестве инварианта при переходе к дискретной модели энергию деформации произвольного элемента среды объемом V :

{ ^f } T№ c Р": И dv ^,                                                    (2)

V где {б}c и {f}c определяются по формулам (1). В результате энергию элемента в виде графа можем представить, с одной стороны, в виде

(f/ (б! = fxx5d + fyy5l + fxx5u + fyy5r + pyx5d + fxy5l + Pyx5u + fxy5r , ccdxxlyy uxx ryy dyxlxy uyx rxy, с другой стороны, энергия деформации элемента сплошной среды есть

J { o } T { в } dv = J ( ° xx ⁸ xx + О ^yy 8 yy + ^т xy Y xy ) ^dv .                                                ⁽³⁾

VV

Здесь напряжения { σ } и деформации { ε } связываются законом Гука, в двумерном случае записывается как:

который

И = №}, или в развернутом виде <

xx О

Оyy т xy

X + 2 ц

X

X 0

X + 2 ц 0 <8

0 ц

xx I

;_yy > , где X , ц — упругие постоянные

LY xy

Ламе, причем X = E v[ ( 1 + v )( 1 - 2 v ) ] для случая плоской деформации и X = E v ( 1 -v ² )

- 1

для плоского напряженного состояния; ц = 0,5 E ( 1 + v )

-I

¹, v — коэффициент Пуассона,

где r(x,y) = xx2 + y2 — расстояние от произвольной точки элемента до вершины трещины, а — показатель сингулярности напряженно-деформированного состояния в окрестности особых точек разреза; ai, bi, ci, di (i = 0, 1, 2, 3) — подлежащие определению коэффициенты. Предполагаем, что начало локальной декартовой прямоугольной системы координат располагается в вершине трещины, а направление трещины совпадает с направлением оси Ox.

Пусть произвольный элемент среды описывается неравенствами x1 < x < x2, элемента.

Выразим в (5) искомые

„ e x 2 du.

Поскольку 8 = —dx , ^J dx x ₁

коэффициенты y2 dU;

8* "ieydy ’ y1

через деформации сторон этого

⁸ xy = / l udy ’ ⁸ yx = J T^dx ’ то

J о y              -tx y1                                  x1

д u       .                   -a

8 xx =^ = a 0 + a1x + a 2 y + a3 r , дx д u       .                  -a

— = c ₀ + c 1 x + c ₂ y + c 3 r , д y

ди

8 yy =^ = b0 + Ьx + b y + Ь r , дy ди J J J J -a — = d 0 + d 1 x + d 2 y + d 3 r , дx

д u ди

^Y xy = ^ + ^ = ^c 0 д x  д y

+ d ₀ + ( c 1 + d 1 ) x + ( c ₂ + d ₂ ) y + ( c 3 + d 3 ) r ^a ,

подставляя соответствующие выражения из (5) и интегрируя вдоль той или иной грани элемента, получаем

8ux = a0Ax + 0,5 (x2 - x2) а1 + a2yxAx + a3 A1,(6)

8dx = a0Ax + 0,5 (x2 - x12) а1 + a2y2 Ax + a3 A2,(7)

8^ = b0Ay + bl x1Ay + 0,5b2 ( y 2 " y2 ) + b3 B1’

8'„ = b0 Ay + bi x2 Ay + 0,5b2 (y2 - y2) + b3 B2,(9)

⁸ xy = c 0 ^A y ⁺ c i ^x i ^A y ^{+ 0,5} c 2 ( y 2 ^- y 2 ) ⁺ c 3 B i , ⁽¹⁰⁾

• ⁸ xy = c 0 ^A y ⁺ c l ^x 2 ^A y ^{+ 0,5} c 2 ( y 22 ^- y l ² ) ⁺ c 3 ^B 2 , ⁽¹¹⁾ 8 ux = d₀ A x + 0,5 d 1 ( x ₂ ² - x 1 ² ) + d ₂ y 1 A x + d ₃ A 1 , (12) 8 dyx = d ₀ A x + 0,5 d 1 ( x 2 - x 2 ) + d ₂ y₂ A x + d ₃ A 2 , (13)

где   A x = x ₂ - x 1 ;   A y = y ₂ - y 1 ;   A i = J ( x ² + y² )   * dx ;   B i = J ( x ² + y ² )   * dy ( i = 1,2).

x ₁                                                        y ₁

Значения A _i , B _i находим с помощью известных численных процедур.

Из равенств (6), (7) и (10), (11) следует, что

8 d _x -8 U_x = a ₂ A x A y + a ₃ ( A ₂ - A ) ,                                                     (14)

xx xx 2321

a 0 =

- °’ 5<8 xx +8 dx ) „у av °'5 a 3 ( A 1 + A 2 )                                     (15) -      A x        a 1 x c a 2 y c         A x       ’                                        (15)

8 'y, -5 1 y = c , A x A y + c 3 ( B 2 - B 1 ) ,                                                     (16)

с 0 - 0,5 (8L +8 X)              0,5 c.(Bx + B2) xy xy                  ,   31    2 -      ay        c1 xc c2 yc         Ay       ’                                        (17) где xc = 0,5(x1 + x2), yc = 0,5(y1 + y2). Используя (14), (16) и контурный закон для u-компоненты ячейки (Рис. 1, а)

8 ^u -8 ^d +8 ' -8^l = 0,                                                            (18)

xx xx xy xy , получаем

( a ₂ - c 1 ) A x A y + a ₃ ( A ₂ - A 1 ) - c ₃ ( B ₂ - B 1 ) = 0.

При отсутствии в (5) сингулярных членов как контурный закон, так и соотношение

_ „     _ _     д2 и   д2 и                          _ смешанных производных ----=---- дают совпадение коэффициентов: a2 — c,. Будем

• д x д у д у д x

считать, что это равенство справедливо и в рассматриваемом случае. В результате контурный закон (18) будет выполняться при условиях a2 — c,,    c3 = ma3,                                                                   (20)

где m = ( A ₂ - A , ) • ( B ₂ - B , ) 1 .

Поступая аналогично с выражениями (8), (9) и (12), (13), будем иметь 5 r„ -5 ;, = b , A x А у + Ь з ( B 2 - B , ) ,

7               \ JO7 УУ / b =------ -

0            Aу

b ₂ y _c

0,5 b₃ ( B ₂ + B , )

А У

,

5 d_vx -5 “ = d ₂ A x А у + d₃ ( A - A ) , yx yx 2321

0,5(5u + 5d ) yx yx d 0 =

A x

- d,x.

-

d ₂ y _c

-

0,5 d ₃ ( A ₂ + A , ) A x

.

Тогда контурный закон для и -компоненты элементарной ячейки (Рис. 1, б )

5 ^и -5 ^d +5 r -5 ^; = 0 yx yx yy yy

дает ( b , - d ₂ ) A x А у + b ₃ ( B ₂ - B , ) - d ₃ ( A ₂ - A , ) = 0. Отсюда в силу предположений, аналогичных приведенным выше, получаем условия выполнения контурного закона (25):

• b, = d 2,      d3 = b3 m-1.(26)

Оставшиеся связи между неизвестными коэффициентами находим из уравнений равновесия элемента до xx дтxy A            дтxy доуу n

----+----= 0,          ----+= дx дуд

Используя (4) и (5), имеем

(X + 2ц) (a, + a 3 D,) + X (b, + b3 D,) + ц ^ c 2 + d 2 + (c 3 + d 3) D2 J — 0,(27)

(X + 2ц) (b2 + b3D2) + X (a2 + a3D2) + ц^c, + d, + (c3 + d3) D, J — 0 ,(28)

где D , и D ₂ — значения частных производных функции r ^-а ( x , у ) по x и у соответственно, вычисленные в центре тяжести элемента.

Далее записываем уравнение (27) дважды с учетом равенств (20), (26):

( X + 2 ц ) a , +X b , +ц ( c ₂ + b , ) + ( X + 2 ц ) a ₃ D , +X b ₃ D , + ц ( ma ₃ + b ₃ m ¹ ) D ₂ — 0,

( X + 2 ц ) a , +X d ₂ + ц ( c ₂ + d ₂) + ( X + 2 ц ) D , c ₃ m ^{- 1} +X d ₃ mD , +ц ( c ₃ + d ₃) D ₂ — 0.

Равенство нулю в этих уравнениях условий

( X + 2 ц ) a , +X b , — 0,

ц b , + ( X D , +ц D ₂ m ^, ) b ₃ — 0, ц d ₂ + ( X m D , + ц D ₂ ) d ₃ — 0 ,

будет соблюдаться, если потребуем выполнения ц c 2 +((X + 2ц) D, +ц mD2) a 3 — 0, ц c 2 +X d 2 — 0,                                 (29)

( X + 2 ц ) a , + ( ( X + 2 ц ) D , m ¹ +ц D ₂ ) c ₃ — 0 .

Зависимости (29) получены путем приравнивания к нулю групп коэффициентов, связанных с нормальными и тангенциальными составляющими напряжений, а также с частными производными функции u (x, у), входящей в контурный закон (18). Из (29)

следует:

a₁ = k₁ b ₁,     b₃ = к ₂ b₁,    a 3 = k 3 c ₂,    c ₂ = k 4 d ₂,    d 3 = k 5 d ₂,     c 3 = k ₆ a₁,

где k 1 = -Х/ ( Х + 2 ц ) , k ₂ = -цДХ D₁ + ц D 2 m ¹) , k 3 =-цД ( Х + 2 ц ) D ₁ + ц Л ₂ m ) , k 4 = -Х/ц , k 5 =-цДх D₁ m + ц D ₂ ) , k ₆ = - ( Х + 2 ц)Дц D ₂ + ( Х + 2 ц ) D₁ m ) .

Уравнение (28) также записываем дважды. Для этого используем равенства коэффициентов (20), (26), реализующих контурные законы (18), (25). В результате находим

Х a ₂ + ( Х + 2 ц ) b ₂ + ц ( a ₂ + d 1 ) + Х D ₂ a 3 + ( Х + 2 ц ) D ₂ b ₃ + ц ( ma ₃ + b ₃ m ¹ ) D ₁ = 0 ,

Х c ₁ + ( Х + 2 ц ) b ₂ + ц ( c ₁ + d 1 ) + Х D ₂ c ₃ m ¹ + ( Х + 2 ц ) D ₂ d ₃ m + ц ( c ₃ + d ₃ ) D₁ = 0.

Как и в предыдущем случае, группировкой коэффициентов и последующим приравниванием к нулю каждой группы, связанной с нормальными и тангенциальными составляющими напряжений, а также с коэффициентами в аппроксимации частных производных функции u(x, у), входящими через посредство (5) в контурный закон для и -компоненты (25), получаем: ц d1 + ((Х + 2ц) D2 + ц D1 c3 m 1) b3 = 0, (Х + 2ц) b2 + ((Х + 2ц) D2 m + ц D3) dз — 0 .

Отсюда следует, что

( Х + 2 ц ) b ₂ +Х a ₂ = 0, ц d 1 + Х c ₁ = 0,

ц a ₂ + ( Х D ₂ + ц m D ₁ ) a ₃ = 0,

ц c + ( ц D ₁ +Х D ₂ m ¹ ) c ₃ = 0,

b ₂ = k 1 a ₂,   a ₃ = k 7 a ₂,    b ₃ = k 8 d ₁,     d 1 = k 4 c ₁,   c ₃ = k ₉ c ₁,    d ₃ = k ₁₀ b ₂,                  (31)

где k ₇ =-цДц D ₁ m + Х D ₂ ) , k 8 = -цД ( Х + 2 ц ) D ₂ +ц D ₁ m ¹) , k 9 =-цДц D ₁ +Х D ₂ m ¹) , k ₁₀ =- ( Х + 2 ц )Д ц D ₁ + ( Х + 2 ц ) D ₂ m ) .

Используя (14), (16), (21), (23) и выражая a ₃ , b ₃ , c ₃ , d ₃ в силу (30), (31)

через a,, ,   b ,    c ,    d,, ,  соответственно,  имеем:    51 -5 “ = a . A x A у + a.k ( A. - A ) ,

2  1  1  2                  xx xx 22721

5 Гу -S t, = b 1 A x А у + b 1 k 2 ( B , - B 1 ) , 5 rу -s; = qA x А у + c 1 k , ( B , - B^ , 5 dx -6 ux = d 2 A x А у + d 2 k 5 ( A 2 - A 1 ) .

Отсюда следует:

5 ^d -5 ^u xxxx a ² = к ’ 11

5 r -5 ^

yy yy b1 =    к , k12

c ₁

5 r -5 "

xyxy k13     ,

d ₂ =

где      k ₁₁ = A x A у + k 7 ( A ₂ - A ₁ ) ,      k ₁₂ = A x A у + k ₂ ( B ₂ - B ₁ ) ,

5d -5u yx yx k14     , k13 =

k ₁₄ = A x A у + k 5 ( A ₂ - A ₁ ) . Из соотношений (15), (17), (22), (24)

A x A у + k 9 ( B ₂ - B ₁ ) , после некоторых

5“ +5 d.    .

преобразований получаем: a ₀ = ^x 2 A x ^xx - b₁k₁x _c - a ₂ у _е

^k 7 a 2 ( A 2 ^{+ A} 1 )

2 A x

,

^{- d} 2 ^k4 у _с

k₉c ( B ₂ + B )       ⁵_W^{+ 5}_W ,      ,

^{9 1} \ ² —-, b = ^уу , ^уу - bx -а^кy_r , 0                1 x c a 21 y c

-

k 2 b 1 ( B 2± B^

2 A у

,

5'

^d 0 =-

5^ +5 Гу c0 = ^AT " c1 xc

' u . +51

^lA x ^ ^{- c} 1 ^k 4 x c ^{- d} 2 у _с

-

kd , ( A + A )

--2a x   ’ Все другие коэффициенты в (30), (31) коэффициенты (32): a ₁ = k ₁ b ₁, a ₃ = k ₇ a ₂, b ₂ = k₁ a ₂, b ₃ = k ₂ b ₁, c ₂ d 3 = k 5 d 2 .

также выражаем через

= k ₄ d ₂, c ₃ = k ₉ c ₁, d ₁ = k ₄ c₁ ,

Найденные значения коэффициентов позволяют представить относительные деформации внутри прямоугольного элемента через абсолютные деформации его сторон:

где

to = [L]{6} c, r [£11 £12 £13 £14  0   0   00

[L]= £21 £22 £23 £24  0   0   00

0000 £„ £„ £_ £_

35   36   3738

; элементы матрицы [ L ]

имеют вид:

^£ 11 = 1/ ( ^{2 А х} ) ^{+ [} У - У с - k 7 ( A 2 ^{+ A} 1 )/( ^{2 А х} ) ⁺ k 7 r "“ ] Ik ^£ 14 = ^{- £} 12 , ^£ 21 = ( У - У с ) k 1 /41 , ^£ 22 = 1/ ( ^{2 А} У ) -^{[ Х} -

1 ,      ^ 12 =^- ( ^{X - X}c ) k 1 / k 12 ,

4а = 1 А х - £_m

'c ^{- k} 2 ( B + B )/( ^{2 А} У ) + Цr "“ ] Д2 , ^£ 23 =^{- k} 21 ,

^k 24 = 1 а У - У 22 , У 35 =V ( 2 А х ) +[ ( 1 + k 4 )( У - У с ) - k 5 ( A + A 1 )/( 2 А х ) + ^ 5 r ’“] ^4 ,    ^ 36 = 1 ( 2 А у ) +

+[ ( 1 + k 4 )( х - X c ) - k 9 ( B 2 + B 1 )/( 2 А У ) + k 9 r -“]/ k 13 , £ 37 = 1 А х - У 35 , £ 38 =1/ А y - £ 36 .

Подставляя { s } из (33) в (2), получаем: { f } c ^T{ 6 } _c = j { o } [ L ]{ 6 } cd^v = j { a } [ L ] dv { 6 } c .

T

v                   V V            7

Сокращая последнее равенство на { б } _с и осуществляя операцию транспонирования, имеем { f } c = j [ L ] { о } dv , а учитывая (4), получаем { f } c = j [ L ] [ C ][ L ] { 6 } cdv . VV

В результате уравнение состояния элементарной ячейки приобретает вид: { f } , = [ K ] c { 6 } с ,

где

[K ] c = №T №] dv.

V

Элементы матрицы [ K ] _c

находятся в результате матричного умножения и

последующего численного интегрирования с помощью квадратурных формул Гаусса с использованием известных табличных значений координат пробных точек и весовых коэффициентов [14].

4. Уравнения графовой модели тела

Граф всего тела строится по тому же принципу, что и графовый элемент, и является результатом операции объединения элементарных ячеек. На рисунке 2 представлен граф тела, состоящего из четырех элементов.

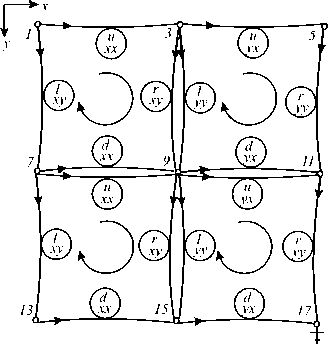
Рис. 2. Граф тела из четырех элементов: u -компонента ( а ); υ -компонента ( б ); точки 17 и 18 – корни подграфов

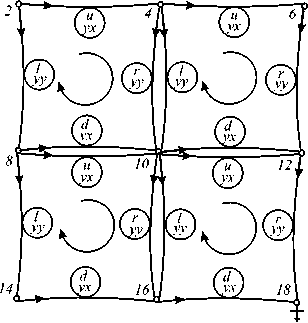
Тело, представленное в виде отдельных элементов, и соответствующая ему совокупность элементарных ячеек описывается уравнением

{ f } = [ K ] { б } .                                                                                 (36)

Здесь {f} и {б} — векторы внутренних сил и деформаций {f }Т ={ fc, f2Tc, f 1 ' ..., nc J ,

{ ^б } ^Т = { ^б 1 ^Т с , ^бТ с ,..., ^б Т с } , причем { ^f } Т , { ^б } Тс

определяются по формулам (1); [ K] —

глобальная несвязная матрица жесткости тела, представленного в дискретном виде: [ K ] = diag[ K 1 _с , K _{2 с} ,..., K _пс ], где [ K ] _ic имеют вид (35), а n — число ячеек, образующих граф.

В общем случае с помощью уравнения (36) определить деформированное состояние нельзя, поскольку заданными, как правило, бывают внешние силы и перемещения. Уравнения связного тела находим путем преобразования обобщенных координат, описывающих разрезанное на элементы и связное тело [10]. Для этого вводим преобразования переменных с помощью квадратных матриц дополнений [ A B ] и маршрутов [ P C ], получаемых сочленением матриц инциденций [ A ] и хорд [ В ], а также матриц путей [ P ] и контуров [ С ] [15]:

{F} = [A _B ]{f} = ^ A ] {f} = ( Af ) ,                                                      (37)

{ A } = [PC] { 6 } = [ C ] { 6 } = ( C6 ) .                                                         (38)

Поскольку матрицы дополнений и маршрутов несингулярны, то с учетом равенств [PC ]Т = [Ab Г1 и [Ab ]Т = [PC ]1 возможны обратные преобразования без выполнения процедур численного обращения:

{ f } = [ A b ] ^{- 1}{ F } = [ PC №}, { б } = [ PC ] ^{- 1}{ A } = [ A b ]^T{ A }.

Подставляя в правую часть (36) найденные значения { 5 } и умножая его слева на [ A_b ] , получаем уравнение, описывающее состояние связного тела:

{ F } = [ A b ][ K ][ A b ] ^{- 1}{ A },

где [ A b ][ K ][ A b ] ^{- 1}

A I K ] [ A T , B ^T ]- aka

akb ^t

BKBT

Рассмотрим вектор (37). Его член [A]{f}, согласно вершинному закону, представляет собой вектор вершинных переменных {F}e, которые идентифицируются как заданные внешние силы. Член [B]{f} отвечает дугам графа {f}b, являющимся хордами, которые отождествляются с неизвестными внутренними силами.

Вектор общесистемных перемещений { A } (38) включает в себя блок [ P ]{ 6 }, который является перемещениями { U } узловых точек в глобальной (заданной для всего исследуемого тела) системе координат. Действительно, если используем контур, в который входит путь от данной вершины к корню и внешняя дуга, связывающая ту же вершину с корнем, то получаем: [ P ] { б } = { U }. Из контурного закона также следует, что член [ C ]{ 6 } равен нулю. В результате уравнение (40) принимает такой вид:

F e f b

AKA ^Т BKA ^Т

AKB ^Т

BKB ^Т

0 ) , откуда следует

{ F } e = [ A ][ K ] [ A ] ^{- 1} { U } = [ K , ]{ U }. Решение

последнего уравнения получаем в виде {U} = [Ks ] 1{F} e, где [Ks J1 — матрица, определяющая связь между вектором внешних сил и вектором перемещений. Используя найденные узловые перемещения, далее с помощью соотношений (33) и (38), (39) определяем поле деформаций и затем по формулам (4) вычисляем поле напряжений в каждом элементе.

5.    Численные результаты

Рассматривается прямоугольная пластина с центральной трещиной, перпендикулярной оси y , при равномерном растяжении (Рис. 3, а ). Характеристики пластины: модуль упругости E = 10000 МПа, коэффициент Пуассона ν = 0,3, ширина W = 240 мм, высота H (в диапазоне от 0,4 W до 2 W ). Трещина имеет длину a . Граничные условия задачи формулируются следующим образом: полагается u = 0 при х = 0; υ = 0 при y = 0 вне разреза; остальной контур и стороны, параллельные Оу , свободны от напряжений. Изучается плоское напряженное состояние пластины. Ввиду симметрии рассматривается четверть расчетной области (на рисунке 3, а заштрихована).

Исследуемая область разбивается на 336 прямоугольных элементов. В окрестности вершины трещины используются 2 сингулярных (графовых) элемента размером (мм) 0,4 × 0,2 . Во всех других элементах применяется линейная аппроксимация деформаций. В расчетах при моделировании сингулярности напряжений особенность описывается как r ^{- 0,5} . Вид пластины после деформирования показан на рисунке 3, б .

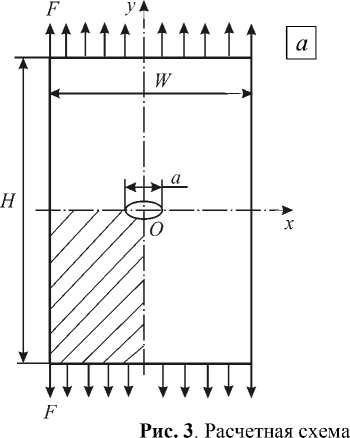
( а ) и деформированная сетка ( б )

Исида [16] получил приближенное решение этой задачи, используя представление комплексных потенциалов Колосова–Мусхелишвили в виде рядов Лорана. Далее (см. таблицу) приводятся результаты расчетов коэффициента интенсивности напряжений (КИН), полученные автором данной статьи и Исидой. КИН вычислены в зависимости от отношения высоты пластины к ее ширине ( HW ). Каждому отношению длины трещины к ширине пластины ( aW ) ставится в соответствие три строки таблицы. Верхние строки содержат данные Исиды, средние — значения, полученные графовым методом с использованием сингулярной ячейки, нижние — отношения авторских результатов к данным Исиды ( δ , в процентах).

Кривые относительной погрешности вычисления КИН в зависимости от HW при различных aW , найденные с использованием указанных методов, представлены на рисунке 4. Для определения КИН применялся энергетический инвариантный интеграл Черепанова–Райса. Как видно из таблицы, результаты расчетов (особенно при HW > 1 ) хорошо согласуются с данными Исиды [16].

Таблица. Сравнение коэффициентов интенсивности напряжений

	H / W
	0,4	0,5 \	0,6 \	0,7 \	0,8	0,9 \		1,0	1,2	1,5 \	1,8 \	2,0 1
a / W	Значения коэффициентов
0,2	1,256	1,175	1,130	1,103	1,083	1,067	1,055		1,039	1,029	1,025	1,025
	1,287	1,174	1,127	1,097	1,081	1,064	1,045		1,030	1,021	1,019	1,014
	102,4	99,9	99,7	99,5	99,8	99,7	99,1		99,0	99,2	99,4	98,9
0,3	1,520	1,371	1,285	1,228	1,184	1,150	1,123		1,088	1,066	1,060	1,058
	1,622	1,396	1,286	1,230	1,200	1,163	1,128		1,100	1,075	1,069	1,065
	106,7	101,8	100,1	100,2	101,3	101,1	100,4		101,1	100,8	100,8	100,6
0,4	1,843	1,629	1,497	1,400	1,323	1,262	1,216		1,158	1,122	1,112	1,109
	2,020	1,682	1,515	1,426	1,353	1,288	1,232		1,181	1,137	1,129	1,122
	109,6	103,2	101,2	101,9	102,2	102,1	101,3		101,9	101,3	101,5	101,1
0,5	2,247	1,967	1,773	1,619	1,496	1,403	1,334		1,251	1,203	1,190	1,187
	2,498	2,052	1,811	1,659	1,541	1,439	1,357		1,280	1,225	1,213	1,206
	111,2	104,3	102,1	102,5	103,0	102,5	101,7		102,3	101,8	101,9	101,7
0,6	2,806	2,424	2,123	1,883	1,702	1,572	1,481		1,380	1,320	1,310	1,303
	3,148	2,560	2,195	1,955	1,763	1,624	1,516		1,417	1,348	1,335	1,327
	112,2	104,3	103,4	103,8	103,9	103,3	102,3		102,7	102,1	101,9	101,8
0,7	3,670	3,040	2,550	2,190	1,940	1,780	1,680		-	-	-	1,488
	4,177	3,249	2,659	2,293	2,034	1,852	1,724		1,613	1,540	1,527	1,518
	113,8	106,8	104,3	104,7	104,8	104,0	102,6		-	-	-	102,0

δ, %

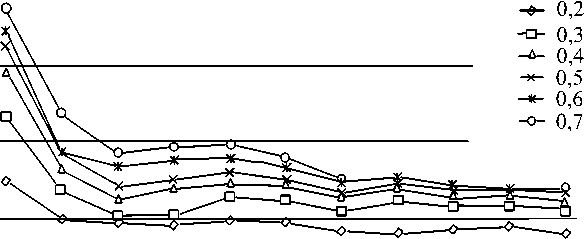
Рис. 4. Сравнительная погрешность графового метода и результатов Исиды [16]

по

95 __________________________________________________________

0,4    0,5 0,6 0,7 ' 0,8 ' 0,9 1,0 1,2 ' 1,5 ' 1,8 ' Н !W

6.    Заключение

Рассмотрена дискретная модель упругого тела в виде ориентированного графа и предложен элемент для описания особенности в напряжениях, которая возникает вблизи вершины трещины. Вывод определяющей системы уравнений основан на использовании фундаментальных законов Кирхгофа для графов и применении специальным образом сконструированных несингулярных взаимно обратных матриц. Графовый метод позволяет построить линейную или сингулярную аппроксимации деформаций (соответствует квадратичной функции перемещений) на четырехузловом прямоугольном элементе с 8 степенями свободы. В традиционном подходе на основе метода конечных элементов для такой аппроксимации требуется элемент, имеющий 8 узлов (16 степеней свободы). В результате определяющая система уравнений графового метода содержит уравнений примерно в 3 раза меньше по сравнению с системой, выведенной традиционным способом МКЭ.