Синхронизация автогенератора с дробной обратной связью

1 . В настоящее время формируется новый раздел теории динамических систем – дробная динамика [1] (в англоязычной литературе – фрактальная динамика [2]). Он охватывает исследования систем с интегро-дифференциальными уравнениями движения дробного порядка.

Учитывая роль осцилляторов в классической динамике, есть все основания рассматривать фрактальный осциллятор как базовую модель дробной динамики. В научной периодике можно найти ряд публикаций, посвященных различным вопросам динамики фрактальных осцилляторов. В частности, в монографии [3] приведены аналитические решения задачи Коши для линейных консервативных осцилляторов. Импульсная характеристика осциллятора с дробным затуханием получена в статье [4]. В работе [5] описан алгоритм численного анализа механического осциллятора с демпфирующей силой, пропорциональной дробной производной от сме-

щения. Ряд ссылок на оригинальные работы по динамике линейных фрактальных осцилляторов содержится также в библиографическом списке монографии [1]. Вместе с тем нелинейные колебательные системы с дифференциальными уравнениями дробного порядка пока исследованы в значительно меньшей степени.

В статье [6] предложена модель автогенератора томсоновского типа с дробной цепью обратной связи (цепью ОС) и проанализированы его колебания в автономном режиме. Настоящая статья посвящена исследованию режима синхронизации дробного автогенератора на основном тоне внешнего гармонического сигнала. В качестве базовой модели автогенератора с нормальными (недробными) связями использован осциллятор Ван дер Поля.

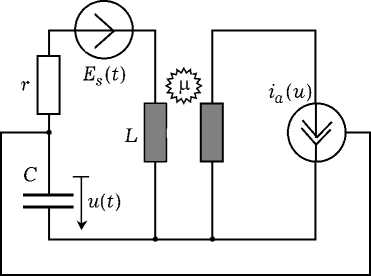
Рис. 1. Эквивалентная схема синхронизированного автогенератора

2 . Модель дробного автогенератора в [6] основана на предположении о том, что ток активного трехполюсника J_a ( t ), протекающий по первичной обмотке трансформатора ОС (см. рис. 1), возбуждает в его контурной обмотке эдс

E c ( t ) = Ц -_LI ^{1 -а} [ J a ( t ) ] , dt

где левосторонний интеграл Лиувилля порядка

1 - а при 0 < а < 1 определяется как

L I ^{1 -а} [ J a ( t ) ] =

Г(1 - а)

t

f

-да

J a (т)

( t -Т) ^а

— т ;

Г( х ) — гамма-функция аргумента ж . Размерный коэффициент ц в дробном дифференциальном © В.В. Зайцев, Ар.В. Карлов, Г.П. Яровой, 2013

преобразовании (1) замещает коэффициент взаимоиндукции M в стандартной модели трансформатора.

С учетом уравнения ОС (1) нетрудно запи-

сать полное уравнение движения автогенератора

при введении синхронизирующего сигнала E_s ( t )

в колебательный контур так, как показано на

рис. 1. Относительно переменного напряжения

(см. таблицы интегралов Лиувилля в [8]), нелинейное слагаемое в правой части (2) принимает форму линейного отклика to2—a gddtLl1—a[ ia (u)] —

to du

• — —2tonAto( A) u +----o--,

• ⁰            Q_ex^ ( A ) dt

u ( t ) на емкости контура оно имеет вид

с зависящими от амплитуды эквивалентными

d2u dt?+

to o du

Q dt

+ too u —

d

^{— to} o “ g^L I 1 ^a [ i a ⁽ u ) ] ^+to 0 E s ⁽ t ), dt

где to o и Q - собственная частота и добротность колебательного контура с характеристическим сопротивлением Z ₀. Нелинейная вольт-амперная характеристика (ВАХ) активного элемента в (2) аппроксимируется кубическим полиномом с коэффициентами S ₀ (малосигнальная крутизна ВАХ) и в (коэффициент нелинейности):

параметрами

Q ex^ ( A )

— gS 1 ( A )sin

Ato —

,

— to o gS 1 ( A ) cos

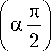
Параметры имеют простую физическую интерпретацию: Q_ex^ ( A ) – модуль внешней добротности контура, Ato( A ) — поправка на частоту свободных автоколебаний.

Таким образом, в приближении эквивалентной линеаризации уравнение (2) заменяется

Ja(u) — Soia(u) — So (1 -вu2)u. (3) Кроме того, при записи уравнения (2) использован безразмерный параметр глубины положительной обратной связи g = Ц So Zo L"' .

• 3 .    Анализ колебаний в осцилляторе (2) проведем в приближении метода эквивалентной (гармонической) линеаризации. Метод широко используется при решении прикладных задач теории нелинейных колебаний [7]. Условия его применимости – высокая добротность резонансной системы и слабая нелинейность активного элемента. Будем считать эти условия для исследуемого осциллятора выполненными.

В соответствии со стандартной процедурой эквивалентной линеаризации в токе (3) при гармоническом сигнале u ( t ) — A cos(to o t ) учитывается лишь первая гармоника колебаний тока J a ( u ( t ) ) :

Ja (t) « SoS1(A)A cos(toot) — SoS1(A)u(t), где средняя крутизна ВАХ по первой гармонике дается выражением

S1( A) — 1 - 4 в A2.(4)

Тогда с учетом того, что

1 —a                         ¹ I ^п I

LI    Lcos (too t )J — -га sin I too t + aal too уравнением d2u      I 1      1

+ to,— dt2    o V Q QeX (A) J dt

+ ( to o + 2to o Ato( A ) ) u — to o E s ( t ).

При внешнем гармоническом воздействии с амплитудой E и частотой

Es (t) — E cos(tot), решение уравнения (6) представим в виде

u ( t ) — A ( t ) cos ( to t + ф( t ) ) .

Амплитуда A и фаза ф принимают постоянные значения для режима синхронизированных колебаний с частотой внешнего воздействия и являются медленными функциями времени для режима биений вблизи границ области синхронизации. Предполагается, что указанные режимы наблюдаются в осцилляторе с дробной ОС, подобно тому, как это имеет место в классическом осцилляторе Ван дер Поля.

• 4.    В режиме синхронизированных колебаний дифференциальное уравнение движения (6) сводится к системе двух алгебраических уравнений для амплитуды и фазы колебаний:

I1              1 I

—

V Q Q .. ( A ) J

A — — E sin ф,

2 (5to(A) — ^) A — E cos ф, в записи которых использованы относительные величины ^ — (to — too)/ too и

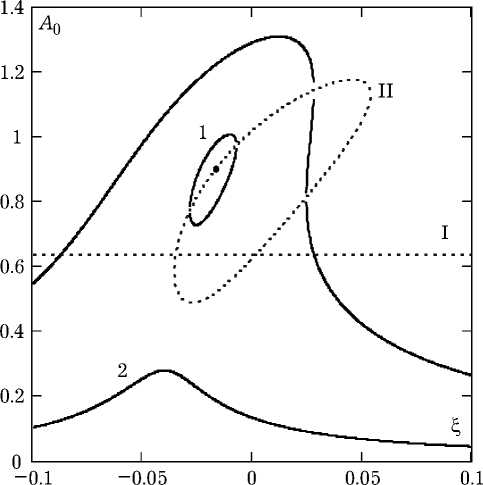
Рис. 2. АЧХ синхронизированного генератора

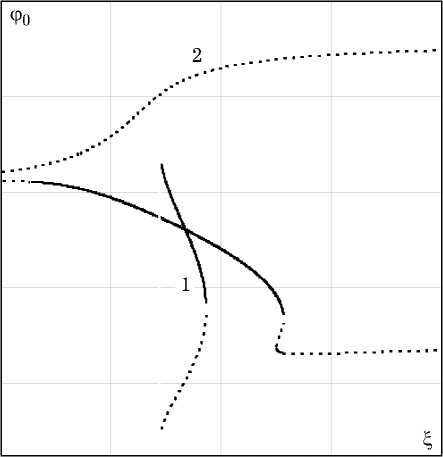
Рис. 3. ФЧХ синхронизированного генератора

0.1

Ato( A )

5to( A ) =------- to o

¹ Г ^П 1 - gS_A ( A )cos a .

2      1 I 2 )

После исключения фазы ф система уравнений

• (7)    дает амплитудное уравнение вида

II A ² + 4 ( 5to( A ) - a² A ² = E ²

I Q QeX (A) J        V или, с учетом (5), вида

Г 1              Г л^² о

• - gSi ( A )sin a A ² +

( Q ^{У 1} I 2^JJ

+ l gS 1 ( A )cos |а^П1 + 2^1 A ² = E 2 .

Для средней крутизны (4) это уравнение является кубическим относительно квадрата амплитуды, поэтому в зависимости от расстройки ^ оно имеет либо один, либо три вещественных корня.

На рис. 2 приведены графики амплитудночастотных характеристик синхронизированных колебаний, построенные по результатам решения уравнения (8) для системы с параметрами a = 0,5, Q = 30 и g = 0,12. Амплитуды сигналов нормированы на величину A * = 1 / д/р. При амплитуде внешнего сигнала E = 0,013 график АЧХ распадается на две ветви: ветвь 1 в форме замкнутой кривой и ветвь 2 резонансной формы. При увеличении амплитуды синхронизации две ветви сливаются в одну – резонансную. На рис. 2 характеристика такого вида построена для E = 0,075. Результаты исследований (см. ниже) показывают, что устойчивыми являются

части АЧХ, расположенные вне области, ограниченной замкнутой кривой II, и выше прямой линии I. Фазочастотные характеристики, соответствующие АЧХ рис. 2, приведены на рис. 3. Неустойчивые части ФЧХ показаны пунктирными линиями.

Общий вывод о форме частотных характеристик синхронизированного осциллятора Ван дер Поля с дробной ОС – наличие асимметрии относительно частоты свободных автоколебаний. Степень асимметрии увеличивается с уменьшением дробного показателя a. В этом осциллятор с дробной ОС аналогичен генератору с запаздыванием т в цепи обратной связи [9], удовлетворяющим соотношению (1 - a)n /2 = to 0 T.

5. В процессе установления синхронных колебаний и режиме биений амплитуда A и фаза ф полагаются медленными функциями времени,

и для них записывается система укороченных

уравнений

1 dA to 0 dt

1 d ф to₀ dt

A Г—

I ( Q

-^

-

-

gS ₁( A ) sin

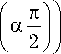
E

- sin ф, 2

-

¹ Г ⁿ

2 gS 1 ( A ) cos la -2

E

2 A

cos

ф.

Уравнения (9) позволяют также исследовать

устойчивость стационарных режимов синхронизированных колебаний с амплитудами и фазами, определяемыми решениями уравнений (7).

Для этого следует положить

A ( t ) = A 0 + a ( t ), ф( t ) = ф 0 + ф( t ),

где нулевыми индексами обозначены стационарные величины, и линеаризовать уравнения (9) относительно малых вариаций a ( t ) и ф( t ). Результатом линеаризации является система

1 da             л 1 d Ф            л

--г; = Р 11 a + Р 12 ^ф,-- = = Р 21 a + Р 22 ^{ф (10)} to g dt                     to g dt

с зависящими от амплитуды A0 коэффициентами p11( Ag) = — ~ + g    (u1( Ac) Ag )sin I agJ,

2 Q 2 dA g                у 2 у

Р 12 <«. A g ) = 5 A g + g S 1 ( A g ) A g cos I a У,

Р 21 (5, A g ) =

—

- . « JL ( u ( A ) ) —

A ₀   2 dA ₀   ^{1 0}

g                  i ^п 1

u i ( A i )cos a ,

2 A ₀¹        ( 2 J

1 g I п I p22(Ag) = — gg + “u1(Ag)sinI a— I•

2 Q 2           у 2 у

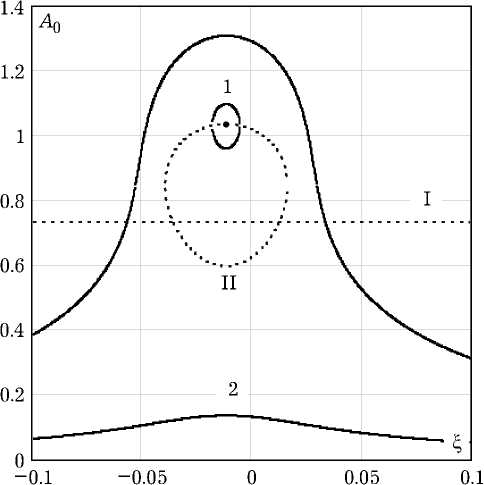
Рис. 4. АЧХ синхронизированного генератора с дробной диссипацией

Необходимым и достаточным условием релаксации вариаций a ( t ) и ф( t ) к нулевым значениям (условием устойчивости A g и ф д ) является выполнение неравенств

D I ⁽ A g ) = ^p 11^{( A} g^{) + p} 22⁽ A g ) ^ ⁰ ,

Dii (5, A g ) = Р 12 (5, A g ) Р 21 (5, A g ) —                (12)

^{— Р} 11⁽ A g ) ^Р 22⁽ A g ) ^ ^g .

1 dA tog dt

1 d ф to_g dt

—

A I 1 . п I sin I a

2 у Q

— gu 1 ( A )

E

— sin ф, 2

г 1 • I Л

—5 — sin a

2 Q у 2

1 E

^— 2 g ^u 1^{( A} )^——cos ф

Равенства в (12) соответствуют границам области устойчивости. Они показаны на рис. 2 пунктирными линиями I и II. Граница D I ( A g ) = 0 представляет собой прямую линию, параллельную оси частот, а граница D II (5, A g ) = 0 — замкнутую кривую второго порядка. При уменьшении дробного показателя a кривая размыкается и граница принимает вид наклоненной вправо линии параболического типа.

и амплитудному уравнению вида

I 1 I П1          12

sin a— — gSi ( A ) A ² +

| Q | 2^{J У B} J

+ 1 —cosI a-| + 25 I A ² = E ².

I _Q I ₂I I

6. Помимо автогенератора с дробной цепью обратной связи, представляет интерес рассмотрение генератора с дробной линейной диссипативной цепью и уравнением движения вида

d2u + О^ d 7 1—a  Y to2 u dt2 Q dt(L     [ J)   0

di ( u )     ₂

= to0 g         + to0 Es(t )• dt

Здесь Q – добротность колебательного контура с нормальной диссипацией, а все остальные переменные и параметры имеют тот же физический смысл, что и в уравнении (2). Описанная выше методика эквивалентной линеаризации уравнения (13) приводит к системе укороченных уравнений

Графики амплитудно-частотных характеристик синхронизации автоколебаний в системе (13), построенные по результатам решения уравнения (14), приведены на рис. 4. Пунктирными линиями показаны границы областей устойчивости стационарных режимов синхронизированных колебаний. Значения параметров АЧХ на рис. 2 и рис. 4 совпадают.

Как следует из рис. 4, частотные характеристики синхронизированных колебаний в генераторе с дробной линейной диссипацией симметричны относительно частоты свободных автоколебаний. Такая симметрия наблюдается и в осцилляторе Ван дер Поля с нормальной диссипацией. Следовательно, дробность линейной диссипации не вносит качественных изменений в характеристики автоколебательной системы.

7. Результаты проведенного анализа позволяют сделать вывод о том, что линейные дробные активно-диссипативные связи в автоколебатель-

ных системах качественно не меняют их динамических характеристик. За счет внесения в схему дополнительных реактивностей они лишь изменяют собственные частоты системы. Качественные изменения в динамике системы возникают тогда, когда дробные связи одновременно являются нелинейными.