Синтез корректирующего контура цифровой системы регулирования низкой чувствительности

Одноконтурные системы автоматического регулирования (САР) широко используются в процессах пищевой и химической технологии.

Улучшить качество переходных процессов в таких системах позволяет оптимизация настроек регуляторов, однако наличие у большинства объектов нестационарных свойств приводит к ухудшению динамики САР со временем их эксплуатации.

К решению данной задачи есть несколько подходов. Первый заключается в проведении повторной идентификации модели объекта управления с последующей перенастройкой регулятора, что не всегда технологически осуществимо. Кроме того, немаловажным является определение момента перенастройки в таких системах.

Второй подход связан с синтезом и реализацией адаптивных САР. Среди недостатков данного подхода можно выделить длительность процедуры текущей идентификации и перенастройки регулятора, что затрудняет использование данных систем, например, для малоинерционных процессов.

Рассматриваемый в данной статье третий подход, заключающийся в применении одного из методов теории чувствительности при проектировании САР, в отличие от приведённых выше обеспечивает требуемые динамические свойства систем в процессе их функционирования.

Свиридов Д.А., 2012

Однако долгое время он не имел практического применения по причине наличия большого числа сложных математических преобразований и вычислений, ограниченных возможностей цифровой вычислительной техники. Современные вычислительные средства, обладая высокой производительностью, дают широкие возможности практического использования методов, основанных на теории чувствительности.

Поэтому актуальной становится задача разработки алгоритма синтеза цифровой САР с применением методов теории чувствительности.

Алгоритм синтеза корректирующего контура. Будем считать, что задана исходная САР, для которой известны передаточная функция (ПФ) замкнутой системы Ф ( s ) (рис. 1) и максимально возможные вариации параметров в течение заданного интервала времени эксплуатации:

**0

Aaj = aj - a p j = 1, g, где a0j – номинальное значениe j-го парамeтра ПФ объeкта; a*j – допустимoe значeʜиe j-го па-рамeтра; g – общee число варьиpyeмых пара-мeтров.

Низкая чувствитeльность САР к проявлe-нию ʜecтационарных свойств объeктa peгули-рования достигaeтся путём ʙʙeдeʜия в замкнутую систeму дополнитeльногo ʙʜeшʜeго кор - ректирующего контура (рис. 1), в котором реализуется компенсация дополнительного движения системы за счёт использования функций чувствительности [1].

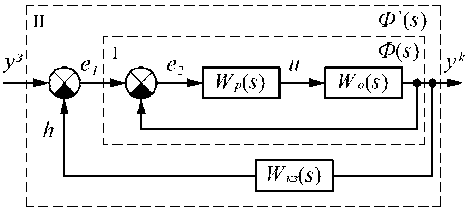
Рис. 1. Структурная схема одноконтурной САР низкой чувствительности: I - основной контур; II -корректирующий контур; W p ( 5 ), W o ( 5 ), W _кз( 5 ) - ПФ регулятора, объекта и корректирующего звена (КЗ); Ф ( 5 ) - ПФ замкнутой системы; Ф '( 5 ) - ПФ замкнутой системы с КЗ; У - задающее воздействие; e 1 , e₂ -величины рассогласований; и - управляющее воздействие; У - выход САР; h - коррекция задающего воздействия

Анализируя функции чувствительности

д Ф (5)

---—, j = 1, g, входящие в состав логарифми-д aj ческих функций чувствительности:

u ^{( 5} ). =

д ln ( Ф ( 5 ) ) д Ф ( 5 )    a j

д ln ( a j )

д a j Ф ( 5 ) ,

j = 1, g , (7)

ПФ замкнутой системы с КЗ имеет вид

можно определить степень влияния каждого параметра модели объекта регулирования на динамические свойства САР [2] и включить в закон коррекции только необходимые функции (7).

Используя приведённую модель чувствительности (МЧ) (7) - совокупность отобранных логарифмических функций чувствительности, преобразуем уравнение (6) к следующему виду:

. . g А a, д ln ( Ф ( 5 ) )

А Ф ( 5 ) = Ф ( 5 )^ - j   ⁽    ) . (8)

j = 1 a j     д ln ( a j )

Подставив уравнение (8) в (5), получим ПФ КЗ со связями по функциям чувствительно-

сти:

0 '( 5 ) =------ . ^{( 5} ) , . .

1 + О ( 5 ) • W^ ( 5 )

Отклонения параметров ПФ объекта в

исходной системе приводят к вариации А Ф ( 5 ),

что влечёт за собой изменение ПФ (1):

_{0 5} . =       ⁰ ( 5 ) + ^{А 0} ( 5 )

’ 1 + ( О ( 5 ) + А 0 ( 5 ) ) • W -_s ( 5 )

.

g А a * д ln ( Ф ( 5 ) )

= 1 a 0     д ln ( a, )

W_k3 ( 5 ) =---------. (9)

Ф ( 5 )      g А aj д ln Ф ( 5 ))

¹ jУ •^ Ы

При получении итоговой формулы (9)

Определим ПФ КЗ, используя условие компенсации дополнительного движения САР:

Ф '( 5 ) = Ф ( 5 ) .                  (3)

Подставив условие (3) в уравнение (2),

получим:

О ( 5 ) =      ⁰ ( ⁵ >  ^{+А 0 ( 5} ) „ .

' 1 + ( 0 ( 5 ) + А 0 ( 5 ) ) • W „ ( 5 )

Из уравнения (4) выразим ПФ КЗ:

W ( ₅ ) =_______ ^{А 0 ( 5} ) _______

0 ( 5 ) • ( 0 ( 5 ) + А 0 ( 5 ) ) ’

допущением является замена неизвестных текущих А a j и a j на заданные А a * и a 00 при расчёте МЧ (7) и вариации А Ф ( 5 ) (8). В противном случае необходима процедура текущей идентификации и дальнейшая постоянная перенастройка коэффициентов ПФ (9).

С учётом формулы (9) полная структурная схема системы с корректирующим контуром со связями по функциям чувствительности примет следующий вид (рис.2) [1].

или в следующей форме:

W ( 5 _Д_. ^{А 0(}5 )/*) . ^e?v ’ 0 ( 5 ) 1 + А 0 ( 5 )/ 0 ( 5 )

С точки зрения теории чувствительности вариацию А Ф ( 5 ) можно расписать следующим образом [1]:

g д Ф (5)

А Ф ( 5 ) = 1—^А _fly ,      (6)

j = 1 д a j

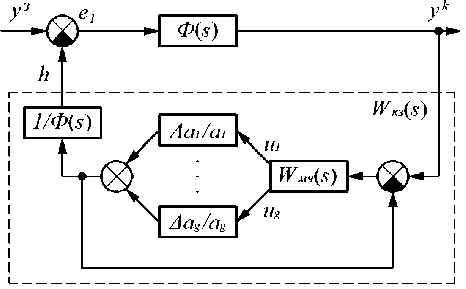
Рис. 2. Полная структурная схема одноконтурной САР со связями по функциям чувствительности: W_M4 ( 5 ) - модель чувствительности; и 1 , ..., u_g - выходы МЧ

где А a j - текущие вариации параметров САР.

Дискретное математическое описание алгоритма. Для реализации корректирующего контура САР низкой чувствительности (рис. 2) с помощью средств цифровой вычислительной техники необходимо иметь математическое описание в дискретной форме КЗ, для получения которого необходимо представить ПФ (9) в

Исследование работоспособности алгоритма. В качестве объекта для исследования работоспособности алгоритма синтеза корректирующего контура цифровой САР низкой чувствительности примем модель основного кана

следующем виде:

W k3 ( s ) =

^а п • s n + ^а п - 1 • s n ^{- 1} + ... + « 1 • s + ^а 0    (₁₀)

P m • S m + P m - 1 • S m ^{- 1} + ... + P i • S + в о

ла системы управления процессом синтеза аммиака в четырёхполочном реакторе: «расход по байпасу азотоводородной смеси - температура в слое катализатора» [4].

ПФ объекта и ПИ-регулятора соответ

Следует отметить, что в формуле (10) а ₀,..., a n и P ₀,..., P m являются функциями

ственно равны:

только номинальных значений параметров ПФ объекта a 0 и их максимальных вариаций

W o ( s ) = T . ■ • W p ( s ) =+ Т

ПФ замкнутой системы:

A a * , j = 1, g .

Воспользовавшись тем, что ПФ КЗ

, . ~                       h ( ^s )

(рис. 2) есть отношение , \ \ , перейдём к y k ⁽ s )

дифференциальному уравнению:

Ф ^{( s} ) =

к -к ■ s + k -к ор    оi

T • ^{s 2 +} ( ^ко^-к р ⁺ 1 ) • ^{s + к}о' ^ki

Для получения параметров дискретных моделей [3] примем такт квантования T ₀=2 с и воспользуемся формулами перехода (13):

P,/-^ + Л .' m dt m m ^{— 1}

d m ^{— 1} h ( t )

dt m ^{— 1}

+ ... +

a = TL^Tl b = kATL

Г ’ T ’ T 1                 T 1

q 0 = ^kp , q i = ^ki- T 0 ^{- k}p ,

+Pv

dh (t)    о , / x

,, + p0 •h(t) = dt

где a , b - параметры дискретной модели объекта; q ₀, q 1 - настроечные параметры цифро

= ап

d n y k ( t )

——— + а

d n ^{— 1} y k ( t )

+а 1 •

dtⁿ dy^k ( t ) dt

^П — ¹ ' df — ¹

^{+ а} 0 ^- y k ⁽ t ).

+ ... +

При малых тактах квантования T ₀ из дифференциального уравнения (11) можно получить разностное путём дискретизации. Приближённо заменим дифференциалы в уравнении (11) правыми разностями [3]:

вого регулятора.

Настройки q ₀, q 1 рассчитаны из условия минимума интегральной квадратичной ошибки.

Численные значения номинальных и возможно допустимых значений параметров модели объекта регулирования, а также их максимальные вариации приведены в табл. 1.

Pm’

A m h i

m

T 0

_R     A m ^{— 1} hi

^{+ P} - —Г    - —1   ⁺ ... ⁺

T 0

. Ah

^{+ P} r "V" T0

+ P 0 Л =

= ап

A n

yk

— + а

n

T 0

n - 1

A n ^{- 1} y k

----v- +... + rp n — 1

T 0

A y*       k

+ а1 • — + а0 • yi .

T 0

Уменьшим текущий индекс такта квантования на единицу в левой и правой частях уравнения (12) и выразим из него h i :

P 0 ,..., P - , h — ! ,..., h - - , kk

.

Таблица 1

Πaрaметры модели объектa

Параметры		Номинальные значения параметров ПФ объектa	Максимальные значения вариаций параметров ПФ объектa	Допустимые зʜaчения пaрaметров ПФ объектa
о S са о о § к	kо	3,4 ° С/%	-20%	2,72
	T 1	102 с	+15%	117,3
S У & г^	a	0,98	+0,003	0,983
	b	0,067 ° С/%	-0,021	0,046

Неизменные при моделировании оптимальные настройки аналогового и дискретного регулятора:

к_р = 1,34; k_i = 0,044;

Представим ПФ (16) в форме дифференциального уравнения:

в d 3 h (t t^^B в3 •        +в2 •

d ² h ( t )

q о = 1,34; q i =- 1,251.

Далее составим МЧ, для чего определим функции (7), которые будут входить в закон коррекции:

_ 6In(О (s)) _

()1= d in (ко) "

( Т • s +1)- s

T 1 • s ² + ( k 0 • k p + 1 ) • s + k о • ki

_ aIn (0 (s)) _

( 1      a in (т)

= а 4 •

От

- T 1 • s ²

^Т1 • ^{s 2 +} ( ^к о • k p ⁺ 1 ) • ^{s + к} о • k i

Подставив МЧ (14) в формулу (9), выведем ПФ КЗ:

W ( s ) = А- ^{e?V }} О ( s )

А 7 *               А т *

A k      A T

— • u (s)1 + ' • u (s)2

--Ч------Ч-----, (15)

A кA T

1+Т" •u (s )+ /' •u (s )2

где A к * и A Т 1* - максимальные вариации коэффициента усиления и постоянной времени модели объекта регулирования в течение ин

тервала времени его эксплуатации.

Из (15) получим отношение полиномов (1о):

W k3 ( s ) =

4 . ,         3 . _         2 . .

а • s + а • s + а • s + а • s + а

—---------------1------о, (16)

в3 • s3 + в2 • s2 + в1 • s + во

где

а4 =(AТ • к0-Aк* • T1 )• Т;

аз =(AТ • к* -Aк* • T)•(к* • кр + 1) —Aк* • Т;

а 2 = (A Т • к* - A к* • Т1 ) • к* • ki — A к* • (к* • кр + 1);

а 1 =- к * • k i •A к * ;

а о = о;

вз =(A Т • к* -A к* • Т1 - к* • Т1 )• к* • кр;

• в2 = (A Т1 • к* - A ко • Т1 - к* • Т1 ) • к* ' ki —

• — (к*2 • кр + к* + Aко ) • к* • кр ;

• в1 = -(к*2 • к р + к* + A ко ) • к* • к р - к*3 • ki • кр ;

• во =-к* • к/.

+ в1 •

dt ² dh ( t )

dt

+ в о • h ( t ) =

d ⁴ у^к ( t )

dt ^{4    +а} 3

+ а 2 •

•

d ³ у^к ( t )

dt ³

d ² у^к ( t ) dt ²

+

₊ а dy " ( t )

^{+ а} 1--- —. ^(1/)

dt

дифференциального уравнения (17)

перейдём к разностному [3]:

в 3 • h i + i

—

3 • h i + 3 • h i

—

+ в 2 • h i ^{1 1}

+в1 •

h i + 1

= а 4 •

—

—

T То

У м

k

+ а ₃ • y i + ¹

k

+ а ₂ • y i + ¹

^Т о 2 • h + h — 1 Т о² h i - + в о • h =

h

-J-2 +

—

4 • У к + 6 • yt

—

4 ^Т о

3 • у к + 3 • у к — 1 — у к — 2

— 4 • yki-2 + yki-3 +

Т о³

— 2 • у к + y ^1

^Т о

+ а1 •

+

У^к + 1 ^— y^k i

Т То

.

В результате получим сложное разност -ное уравнение третьего порядка относительно h i ^:

в о ,

а 1 ,

..., в 3 , h — 1 ,..., h — 3 , kk

...,

.

Для оценки работоспособности алгоритма получим отклик цифровой САР на единичное ступенчатое воздействие при номинальных значениях параметров модели объекта регулирования. Для этого рассчитаем переходный процесс по заданию в замкнутых системах: без КЗ (18) исКЗ (19):

^ui = ^ui — 1 ⁺ q о • ( У з ^— y ) ⁺ q 1 • ( У в1 ^— y — 1 ) ,

. У1 + 1 = a • У1 ⁺ b • ^ui ,

i = 1, N .

в о ,..., в 3 , h — 1 ,..., h — 3 , kk

а 1 ,

...,

,

^ui = ^ui — 1

+ q о • (yi — hi — yi )

^{+ q}1 • ( ^y! — 1

.yi+1 = a • у" + b • ui,

^— h i — 1 ^{— у к} — 1 ) ,

i = 5, N .

Динамические характеристики в прира-

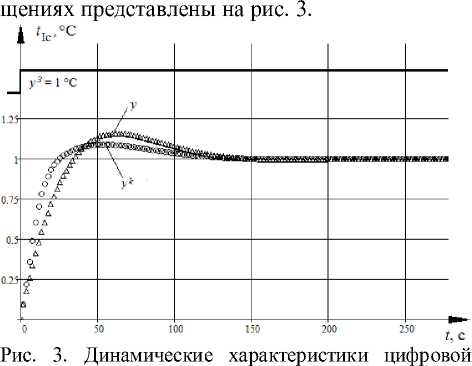
САР при номинальных значениях параметров ПФ объекта: у - замкнутой системы без КЗ; yk - замкну той системы c КЗ

Аналогично осуществим расчёт переходных процессов (рис. 4) замкнутых систем при допустимых значениях параметров ПФ объекта

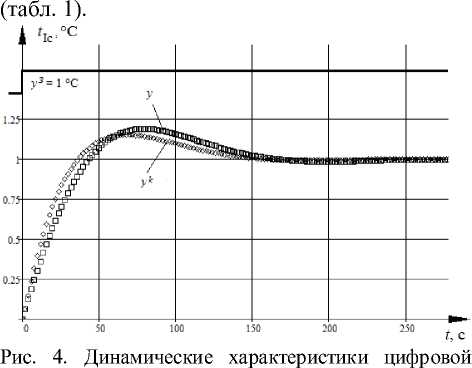
САР при допустимых значениях параметров ПФ объекта: у - замкнутой системы без КЗ; y k - замкнутой системы c КЗ

Проведём расчёт переходных процессов замкнутых систем при следующих промежуточных значениях параметров объекта регулирования:

k = 3,06 °N/%; T 1 = 109,65 c; или в дискретной форме:

a = 0,982; b = 0,056 °N/%.

По критерию

N           \2

^s = ^ ( у■ - y,)

j = 1 осуществим расчёт значений интегральноквадратичной ошибки для всех рассчитанных вариантов (табл. 2).

Таблица 2

Интегрально-квадратичная ошибка

САР	Значения параметров модели объекта регулирования
	Номинальные	Промежуточные	Возможно допустимые
Без КЗ	10,681	12,44	14,56
С КЗ	7,248	9,021	11,24

Переходный процесс системы с КЗ при возможно допустимых параметрах объекта практически полностью совпадает с переходным процессом системы без КЗ при номинальных параметрах объекта. Отсутствие полного совпадения объясняется наличием допущений при синтезе КЗ.

Алгоритм синтеза корректирующего контура цифровой системы регулирования низкой чувствительности работоспособен и обеспечивает требуемые динамические свойства. При увеличении вариации параметров динамическая характеристика системы с КЗ обладает свойством приближения к динамической характеристике системы без КЗ при номинальных параметрах модели объекта.