Синтез линзы Люнеберга с плоской поверхностью с использованием квазиконформных оптических преобразований

С развитием современных технических средств все большую актуальность приобретает использование сверхширокополосных систем радиолокации, навигации и связи, неотъемлемым элементом которых являются антенны, удовлетворяющие ряду критериев:

• a)    работать в широком диапазоне частот;

• b)    осуществлять перестройку направления главного лепестка диаграммы направленности.

Подобные системы могут быть построены с использованием диэлектрических структур, формирующих диаграмму направленности антенны. Такие структуры могут представлять собой диэлектрические (с однородным или неоднородным распределением диэлектрической проницаемости) или металловоздушные линзы [1]. Одной из наиболее известных диэлектрических линз с неоднородным распределением диэлектрической проницаемости является линза Люнеберга [2]. Ее особенность состоит в том, что она обладает сферической симметрией. Это позволяет использовать ее для построения многолучевых антенных систем. Однако шарообразная форма линзы усложняет практическую реализацию подобной системы.

В данной работе предложена диэлектрическая структура, представляющая собой линзу Люне-берга с плоской поверхностью. Подобная структура позволит реализовать простую систему с электронным управлением диаграммой направленности, состоящую из линзы и массива излучателей, расположенных вдоль плоской стороны линзы.

• 1.    Метод квазиконфромных оптических преобразований

Синтез предлагаемой линзы был проведен с использованием метода квазиконформных оптических преобразований.

Суть метода состоит в осуществлении преобразования из так называемого виртуального пространства в реальное . При этом в виртуальном пространстве мы можем расположить диэлектрическую структуру с заранее известными свойствами, а преобразование это должно быть подобрано таким образом, чтобы волновой фронт в апертуре антенны в реальном пространстве соответствовал необходимым нам условиям.

Однако диэлектрическая проницаемость новой структуры, полученной в результате преобразований, требует пересчета.

Пусть задано преобразование

, x = x ' ( x ) , _ У = У ' ( У ) .

Тогда, согласно [3], свойства среды в реальном пространстве будут рассчитываться как

е i 'j j ' =е i ^, j Л i ' л j det ( л i ' ) ,                                  (2)

^{— 1}

Ц i ^- j ц i ^{- J} Л i Л J det ( л i ) ,                               (3)

где Л i - оператор преобразования.

Если основания, обозначенные индексами i и i' , являются координатным базисом, оператор преобразования будет выглядеть как

Л г

д x '

^д x i

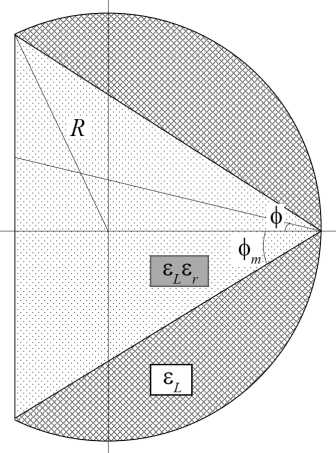
Рис. 1. Построение линзы Люнеберга с плоской поверхностью

Fig. 1. Construction of a Luneberg lens with a flat surface

для функции преобразования координат x i = x i ( X i ) .

Таким образом, мы можем трансформировать

n' = n • tr

исходную диэлектрическую структуру в новую при помощи произвольных преобразований координат (1). Однако, согласно (2) и (3), диэлектрическая и магнитная проницаемость материала преобразованной линзы может стать анизотропной. При этом физическая реализация материалов с анизотропной диэлектрической проницаемостью на настоящий момент является достаточно сложной задачей.

Решить данную проблему помогает методика квазиконформного преобразования - QCTO , которая для некоторых преобразований может позволить синтезировать линзу со свойствами, идентичными стандартным преобразованиям, линза при этом может быть изготовлена из изотропных

" л T Л

12 Л

2. Линза Люнеберга с плоской поверхностью

Классическая линза Люнеберга представляет собой шарообразную структуру с распределением диэлектрической проницаемости, зависящим только от расстояния от центра линзы [5]:

Г r л ² e_L( r ) = 2 - . L^V I R J

материалов.

Суть методики состоит во введении в изначальные преобразование свободных параметров и их оптимизации. Целевой функцией для минимиза-

где r – расстояние до центра линзы; R – радиус линзы.

Для того чтобы сделать одну из поверхностей линзы плоской, было использовано координатное преобразование:

ции в таком случае является tr (Л T л)

K ( x , у ) = - K + - = \ , ^У >  1, ^{( 7)} 2 ( K J      2|Л|

x ' = kx , 1 y = ^ky - z = ^{kz -}

где K =

— > 1, Х₁ ( x , y ) > Х₂ ( x , у ) - собственные

Л;      '

, cosф где k =------L (см. рис. 1). cos ф

Изменяя угол ф _m , мы можем задавать положение «среза» на плоской стороне линзы.

Согласно (2):

T числа матрицы ЛЛ .

В некоторых случаях существует возможность избежать подобных ресурсоемких вычислений. Так, согласно [4], для плоской волны (TEM) или поперечной волны (TE) с вертикальной поляризацией показатель преломления может быть аппроксимирован по следующей формуле:

е' = ЛЛ ^Т det ( л ) ¹ =

<    2

x             xy

xy     x ⁴ + 3 у ² x ² + у ⁴

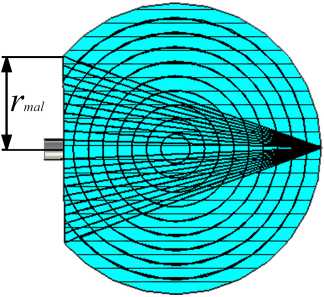
Рис. 2. Улучшенная квазиконформная линза Люнеберга с расположенным на ее срезе возбуждающим волноводом

Fig. 2. Improved quasi-conformal Luneberg lens with an exciting waveguide located at its cut

Используя (7), получим:

• 8 r = -^.                          (11)

• 3.    Результаты моделирования

COS ф m

На основании (11) можно построить модель с изотропными параметрами.

Физическая реализация подобной модели возможна с использованием технологии 3D-печати. Структура с неоднородной диэлектрической проницаемостью может быть получена за счет неоднородности материалов, из которых она изготовлена. Неоднородность диэлектрического заполнения при печати может быть достигнута с неоднородностью самого заполнения (чередования диэлектрика и воздушных прослоек), например с применением технологии, предложенной в работах [6–8]. Соотношение воздушных прослоек и диэлектрика рассчитывается с использованием формулы Лихтенекера [9].

Геометрические размеры модели были выбраны, исходя из рабочей частоты в 8 ГГц, при этом радиус линзы составил R = 300 мм.

Модель представляет собой классическую линзу Люнеберга, один край которой срезан, исходя из выбранного угла ф m , и перпендикулярно срезу структура линзы изменена таким образом, чтобы распределение диэлектрической проницаемости соответствовало формуле

8 = 8 L 8 r , (12) где 8 l - диэлектрическая проницаемость классической линзы Люнеберга, 8 r рассчитана согласно (11).

На основании данных предыдущих исследований [10] количество слоев в линзе было выбрано равным 10 (рис. 2).

Одним из важных параметров построения данной линзы является угол ф , от него зависит, какой диапазон сканирования мы получим при том или ином значении ф . В эксперименте будет использоваться параметр ф = 20 ° , а также ф = 30 ° . Линза с параметром ф = 20 ° является более стабильной и устойчивой, так как при увеличении среза увеличивается и величина боковых лепестков на диаграмме направленности.

На рис. 3 видно, что полученный диапазон сканирования достигает ± 36 ° при угле среза линзы ф = 20 ° . Ключевым результатом стоит отметить низкий уровень боковых лепестков по сравнению с главным, а также отсутствие граничных эффектов на краях линзы. Помимо того, это также свидетельствует о том, что угол среза линзы может

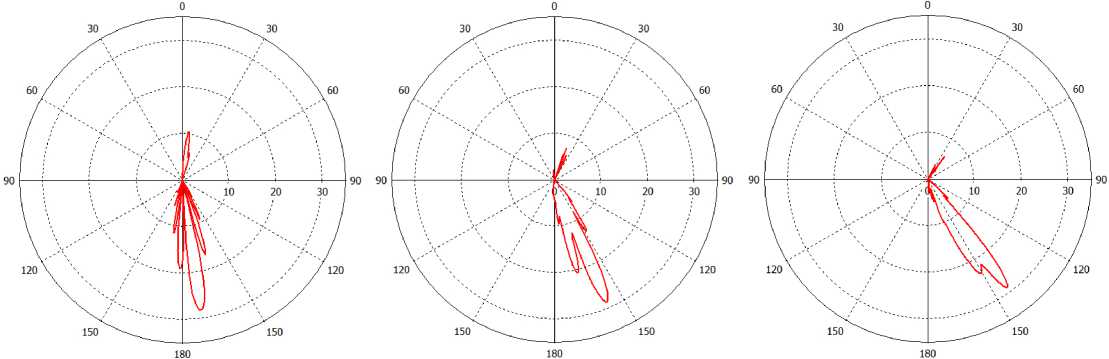
б                                     в

Рис. 3. Диаграмма направленности линзовой антенны для случаев возбуждения волноводом, расположенным на различных рас-

135 стояниях относительно центра: а - r ; б - r ; в - r 6 mal 6 mal 6 mal

Fig. 3. Radiation pattern of the lens antenna for cases of excitation by a waveguide located at different distances from the center: 135 л —   г • п —  г • г —  г _ a rmal ; b rmal ; c rmmal 666

Таблица. Параметры диаграмм направленности для различных расположений возбуждающего волновода

Table. Parameters of radiation patterns for different locations of the exciting waveguide

Расстояние от волновода относительно центра линзы	Угол отклонения главного лепестка относительно центрального направления, °	Уровень главного лепестка, dBi	Уровень побочного излучения, dB	Ширина главного лепестка по уровню –3dB
0	0	28,5	13,2	5,6
1 6 r mal	8	28,2	18,9	5,4
2 6 r mal	16	28,3	19,9	5,4
3 6 r mal	23	28,5	20,6	5,2
4 6 r mal	30	28,5	21,5	4,9
5 6 r mal	36	28,7	23,1	4,5
r mal (волновод на краю среза)	38	28,5	23,8	4,5

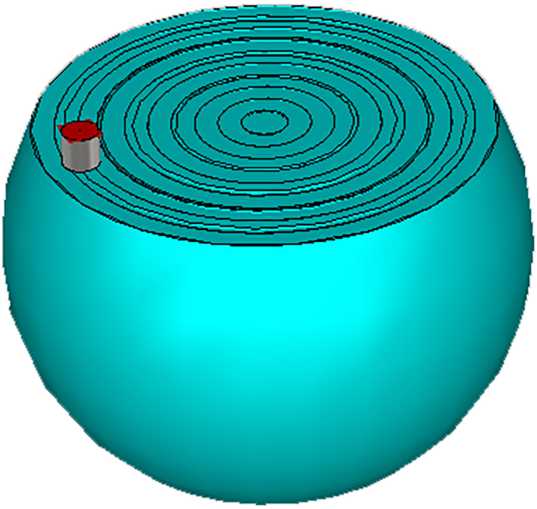
Рис. 4. Улучшенная линза для случая волновода, расположенного на краю плоской поверхности линзы с углом среза θ

Fig. 4. Improved lens for the case of a waveguide located on the edge of a flat lens surface with a cut angle θ быть увеличен для получения больших углов сканирования.

Все результаты зафиксированы при частоте 8 ГГц.

Параметры диаграмм направленности для случаев возбуждения волноводом, расположенным на расстояниях относительно центра, представлены в таблице.

Из полученных результатов следует линейная зависимость угла отклонения главного лепестка диаграммы от смещения волновода относительно центра линзы. Данную линзу можно продолжить «раскрывать», увеличивая угол среза θ . На рис. 4

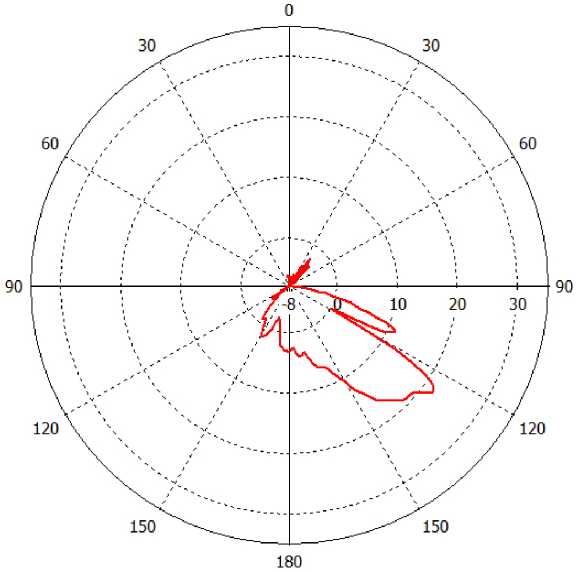
Рис. 5. Диаграмма направленности улучшенной линзы для случая волновода, расположенного на краю плоской поверхности линзы с углом среза θ

Fig. 5. Radiation pattern of the improved lens for the case of a waveguide located on the edge of a flat lens surface with a cut angle θ представлена модель линзы с углом сканирования вплоть до ±60 градусов. Однако это существенно повышает уровень боковых лепестков по отношению к главному с ростом угла отклонения, что можно наблюдать на рис. 5.

Заключение

В ходе работы синтезирована линза Люнеберга с плоской поверхностью с использованием метода квазиконформных оптических преобразований.

С помощью полученной линзы возможно построить сканирующую систему на основании линзы и массива излучателей, расположенных вдоль плоского края линзы.

Однако, углы сканирования данной системы ограничены геометрией линзы, чем больший мак- симальный угол сканирования мы выбираем, тем существеннее становится влияние боковых лепестков на диаграмму направленности. Решение данной проблемы является целью будущих исследований.