Синтез марковской модели термохимической деструкции полимера в растворе

Одним из перспективных новых способов получения низкомолекулярных полимеров является термохимическая деструкция полимеров в растворе. При этом в качестве сырья рассматриваются как товарные каучуки промышленного назначения, так и отходы их производства [1]. Разработка таких технологий требует детального изучения кинетики происходящих химических реакций, в том числе и методом моделирования.

Механизм деструкции представляет собой последовательность случайных событий (элементарных актов разрушения макромолекул) с конечным количеством исходов, которые можно рассматривать как в дискретныемоменты времени, так и непрерывно. При этом вероятность перехода в новое состояние (молекулярно-массовое распределение (ММР) полимера) зависит только от состояния, из которого совершается переход и не зависит от всей предыстории процесса. Для описания такого рода процессов помимо уравнений химической кинетики [1], часто используется математический аппарат теории цепей Маркова [2]. В этом случае рассматривается не кинетика превращения на уровне отдельных макромолекул, а ММР всего полимера, участвующего в процессе деструкции. Случайным событием при таком подходе является совокупность элементарных актов деструкции, а состояниями – диапазоны (фракции) молекулярных масс ММР. Интенсивности переходов из состояния в состояние характеризуют скорость прямых и обратных процессов (деструкции и сшивки, полимеризации).

В работах [3, 4] показано применение аппарата цепей Маркова для описания процессов синтеза полимеров на уровне кинетики превращения отдельных макромолекул. В работе [5] предложено описание процесса разрушения зерен крахмала на основе цепей Маркова, в работе [6] рассмотрено описание динамики массового распределения жировых шариков молока в ходе его деструкции.

Методика моделирования

Предлагается использовать аппарат цепей Маркова для описания непосредственно измеряемого ММР полимера в ходе деструкции. В этом случае рассматривается не кинетика-превращения на уровне отдельных макромолекул, а ММР всего полимера, участвующего в процессе деструкции. Случайным событием будет совокупность элементарных актов деструкции, а состояниями – диапазоны (фракции) молекулярных масс в ММР. При этом интенсивности переходов из состояния в состояние характеризуют скорость прямых и обратных процессов (деструкции и сшивки). Вероятность нахождения в определенном состоянии характеризует количество макромолекул соответствующей фракции ММР, а распределение вероятностей характеризует соответственно ММР полимера. Преимуществом такого подхода является простота описания процесса, возможность использовать измерения ММР полимера методами гель-проникающей хроматографии (ГПХ), не проводя их масштабирования и предварительной обработки, а представление интенсивностей в виде функций режимных параметров процесса деструкции (расходов агента деструкции, температуры и т. п.) позволит создавать алгоритмы управления процессом, ориентируясь на желаемое ММР. В качестве недостатков можно отметить то, что полученные значения интенсивностей переходов будут феноменологическими и «привязаны» к технологическому оборудованию, на котором проводился эксперимент для идентификации значений интенсивностей переходов.

Основываясь на вышесказанном, предлагается следующая модель процесса деструкции полимера. Под действием агента деструкции с течением времени система макромолекул может переходить из одного состояния в другое. Система принимает состояния, которые будут ассоциироваться с диапазоном длин (масс) макромолекул, соответствующих определенной массовой или объемной фракции ММР. Дискретное конечное множество состояний в соответствии с принятой шкалой описывается множеством состояний в виде следующего множества X = { x 1 ,x 2 ,...,x n } , n e N , где x n -числовой диапазон длин ( масс) макромолекул в n- ой фракции.

При синтезе структуры, в рамках теории цепей Маркова, приняты следующие допущения: процесс деструкции последовательный характер; интенсивность перехода из одного состояния в другое отражает интенсивность процесса деструкции и характеризуется величиной λ i,j , а интенсивности обратных переходов равны нулю; процесс деструкции моделируется переходом из состояния x i в x j , где j>i , при этом интенсивностью переходов λ j,i пренебрегаем; состояние сис тем ы характеризуется вероятностью Р i , где i = 1, N, где N - количество фракций [7, 8]. При принятых допущениях граф состояний представлен на рисунке 1. Распределение макромолекул по фракциям соответствует индексам (пусть i =1 фракция с наибольшей молекулярной массой или длиной).

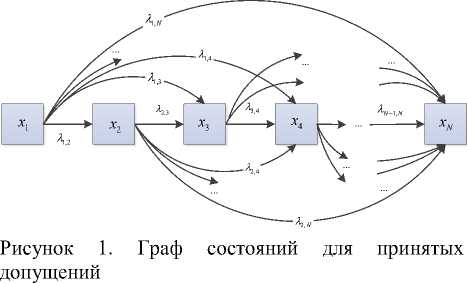
Figure 1. State graph for accepted assumptions

Запишем систему уравнений Колмогорова-Чепмена для графа, представленного на рисунке 1:

dPT -^- 2 j ( ■ ) ;

dP 2 ( t )   „ zx

T ^- Л ,2 ^P1 ⁽ t ) - 2 A i, j^P2 ⁽ t ) ;

^dt                   j - 3

dP. (t)    . „ z x dt - A,P (t) + ^2,iP2 (t) + ... + A-1,iPi-1 (t) -

N

- 2 V. ( t ) ;

j - i + 1

dP t

⁼ ^ 1, n P 1 ( t ) + ^ 2, n P 2 ( t ) + ... + ^ .,n P ( t ) +

+ ... ⁺ A n - 1, n^Pn - 1 ⁽ t ) ;

P 1 ( 0 ) - P 10 , P 2 ( 0 ) - P 20 ,..., P n ( 0 ) - P n ,0 ,...,

P n ( 0 ) - P n ,0 ;

A i , j >  0, i - 1, N , j - 1, N .

где t – время деструкции.

Пусть плотности потоков A i j постоянны, тогда, задаваясь матрицей интенсивностей прямых переходов λ и вероятностей состояний P

N

- 2 A 1, j

j - 2

^A 1,2

0       ...        0

N

^-2 ^A 2, j  ...       ⁰

j - 3

Л-

N

A 2, i

.

.

.

-

2 a , j

A 1, N

j - i + 1

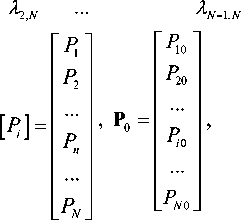
° J

в матричном виде запишем

S = ^Л- ^P ,PI ,- - P 0 .          (3)

В данной записи вектор P ₀ задает начальное ММР полимера до начала процесса деструкции.

Математическая модель

В качестве среды моделирования использована интерактивная графическая среда имитационного моделирования MathWorks Simulink™, позволяющая при помощи блок-диаграмм в виде направленных графов, строить динамические модели, включая дискретные, непрерывные и гибридные, нелинейные и разрывные системы. Кроме того, среда Simulink™ имеет в своем составе инструменты генерирования сигналов различной формы, анализа сигналов во временных и частотных областях, что позволяет осуществлять генерирование, имитацию прохождения и всесторонний анализ сигналов в рамках одной среды моделирования [9]. Преобразование системы дифференциальных уравнений в структурную Simulink™ модель осуществлялось по методике, представленной в [10]. Для интегрирования системы дифференциальных уравнений использовался метод Рунге-Кутта 4/5 порядка в модификации Дорманда– Принца (функция ode45), а в случае большого разброса в значениях интенсивностей метод конечных разностей переменного порядка в сочетании со схемой обратного дифференцирования (метод Гира функция ode15s) [11].

Для оценки параметров математической модели были проведены экспериментальные исследования процесса деструкции полибутадиена в растворе. В качестве исходных данных для оценки ММР полимера использовались данные ГПХ раствора полибутадиена [12]. Из исходной хроматограммы, содержащей 100 фракций усреднением выделено 6 фракций (рисунок 2) . Определение молекулярных параметров и молекулярно-массового распределения образцов каучука осуществлялись с помощью ГПХ. В качестве оборудования для ГПХ анализа применялась система Breeze фирмы Waters. Результаты экспериментальных исследований представлены в таблице 1. Ввиду наибольшей интенсивности процесса деструкции в первый час и необходимости идентификации всех 6-ти фракций ММР разбиение на фракции в ходе процесса деструкции отличаетсяот исходного.

Таблица 1.

Результаты исследований

Research results

Table1.

№ фракции (fraction)	масса M (ln М)	доля	масса (mass) М (lnM)	доля
		0 ч		2 ч	3 ч	4 ч	5 ч
P 6,0	6–7.7	0	31000 (10.34)	0.667	0.887	0.98	0.992
P 5,0	7.7–9.3	0,01	93000 (11.44)	0.234	0.097	0.02	0.007
P 3,0	9.3–11	0,62	155000 (11.95)	0.058	0.016	0	0
P 4,0	11–12.7	0.255	217000 (12.3)	0.02	0	0	0
P 2,0	12.7–14.3	0.39	279000 (12.54)	0.011	0	0	0
P 1,0	14.3–16	0.01	341000 (12.74)	0.01	0	0	0

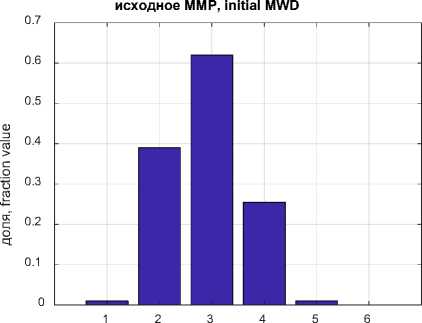
номер фракции, fraction number

Рисунок 2. ММР исходного полимера

Figure2. MWD of the starting polymer

Соответствующий сделанным допущениям граф представлен на рисунке 3.

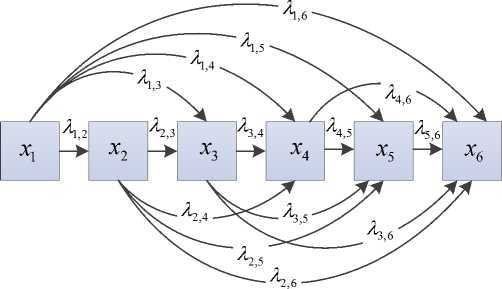
Рисунок 3. Граф, моделирующий процесс деструкции полимера с ММР из шести фракций

Математическая модель процесса деструкции для случая 6-ти фракций описывается системой (4).

dP (?)      6

d -^ ^ ⁽ * ) ;

dP^ l = 2 , P , ( t ) - ± Л,„ , P , ( t ) ;

dPJA  i , . Л

-d* -²= S 2 ,3 P i ( * ) - g V> ( * ) ;

dP T = 1 2 P ( t ) - !    . ( * ) ;

dP 5 ( * )

d* = ^ ^ ,5 ^Pi ⁽ * ) - Л ;,б ^P 5 ⁽ * ) ^;

dP₆(*)    5

"- P ( * ^{) ;}

P , ( 0 ) = P ,0 , P i ( 0 ) = P ₂ ,0 , P 3 ( 0 ) = P 30 ,

P 4 ( 0 ) = P ₄ ,0 , P 5 ( 0 ) = P 5,0 , P 6 ( 0 ) = P 6,o ;

2,, . 0.

I                                                 (4)

где P i , ₀, i = 1..6 задает начальное ММР полимера до начала процесса деструкции из таблицы 1.

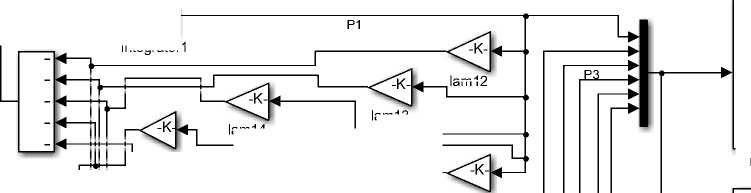
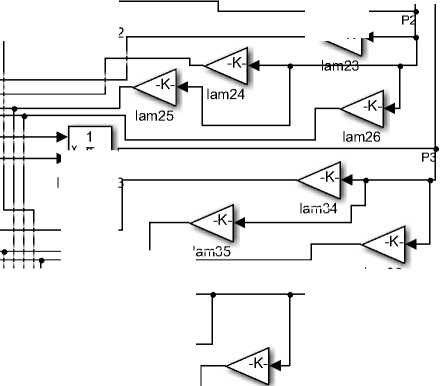
Структурная схема, в формате MathWorksSimulink™, реализующая математическую модель (4) представлена на рисунке 4.

• Figure3.    Graph modeling the process of destruction of polymer with MMP from six fractions

  0.011

  
  

  P2(0)

  
  

  0.02

  
  

  0.058

  
  

  P4(0)

  
  

  0.234

  
  

  P5(0)

  
  

  ntegrator1

  1 ^xo^s

  0.01

  P1(0)

  

  am12

  am13

  am14

  lam15

  
  
  
  
  

  P3(0)

  
  
  
  
  
  

  lam16

  Integrator2

  -K-

  1 ^xo^s

  tr

  

  am34

  lam35

  ^xos

  Integrator3

  lam36

  P4

  Integrator4

  -K-

  lam45

  lam46

  1 ^xo^s

  
  
  

  Integrator5

  
  

  P5

  
  

  0.667

  
  
  
  

  -K-

  lam56

  
  
  
  
  
  
  
  
  
  

  Scope1

  simout

  
  

  To Workspace

  P1

  P2

  P4

  P5

  P6

  
  
  
  
  

P6(0)1

P6

Integrator6

Рисунок 4. Модель Simulink

• Figure4.    Simulink model

Для корректного использования аппарата сетей Маркова были нормированы, исходя из условия

N

E p ( ^= i,             (5)

= 1

где N – количество фракций.

Для этого вводился дополнительно коэффициент нормировки k _норм , на который умножаются значения таблицы 1 для каждого образца, обеспечивающего выполнение равенства (5):

^киорм    N         *                ⁽⁶⁾

E p ( Pi)

= 1

Для численного поиска значений параметров минимизировалось среднеквадратичное отклонение расчетных данных от экспериментальных по каждой фракции

MN ₂

• ⁵ = EE ( j^ эксп — P j (t i ) расч ) -T^ min ,(7) j = i i = i

где M, N – количество фракций и точек контроля при заданном времени деструкции соответственно.

Для минимизации критерия (7) использовался нелинейный метод наименьших квадратов на основе алгоритма Левенберга–Марк-вардта [13] из библиотеки OptimizationToolboxMathWorks™ [14].

Результаты математического моделирования

Результаты численного эксперимента представлены на рисунке 5, где показаны динамика изменения доли каждой фракции во времени (рисунок 5а) и фракционный состав в заданные моменты времени (5б). Погрешность расчётов в среднем составила около 5%, что говорит о приемлемой ошибке оценки изменения долей фракций полимера в ходе процесса деструкции для рассматриваемого процесса и условий. Параметры математической модели (4) (матрица интенсивностей переходов), полученные в результате минимизации критерия (6) представлены в таблице 2.

Таблица 2.

Матрица интенсивностей переходов

Table2.

Transition intensity matrix

λ i,j	p1	p2	p3	p4	p5	p6
p1	0	1.0015	1.0077	1.0395	1.1457	0.88349
p2	0	0	1.0098	1.0687	1.2755	0.84755
p3	0	0	0	1.1516	1.7132	0.73419
p4	0	0	0	0	2.8476	0.082361
p5	0	0	0	0	0	1.3532
p6	0	0	0	0	0	0

номер фракции, fraction numder

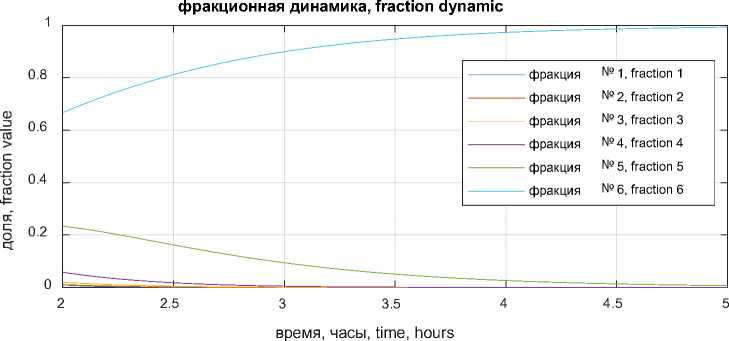
(a)

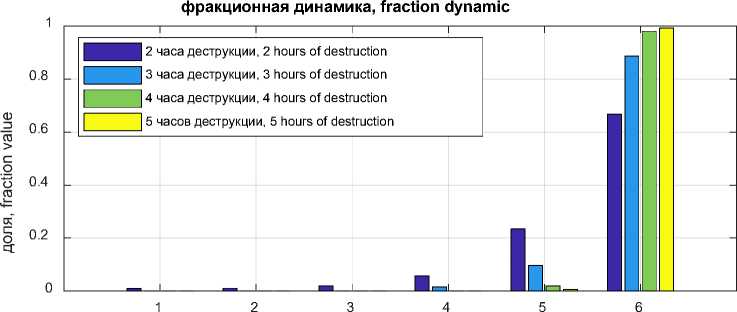
(b)

Рисунок 5. Фракционная динамика в ходе процесса деструкции, (a) динамика изменения доли каждой фракции во времени, (b) фракционный состав в заданные моменты времени

Figure5. Fractional dynamics during the process of destruction, (a) the dynamics of the change in the fraction of each fraction in time, (b) the fractional composition at specified times

Выводы

Как видно из представленных данных предложенная математическая модель качественно верно описывает как динамику изменения долей фракций, так характер изменения фракционного состава. Кроме этого, проведенные экспериментальные исследования и оценка параметров математической модели (6) показали приемлемую погрешность расчетов долей фракций полимера в ходе процесса его деструкции для рассматриваемого процесса и условий.

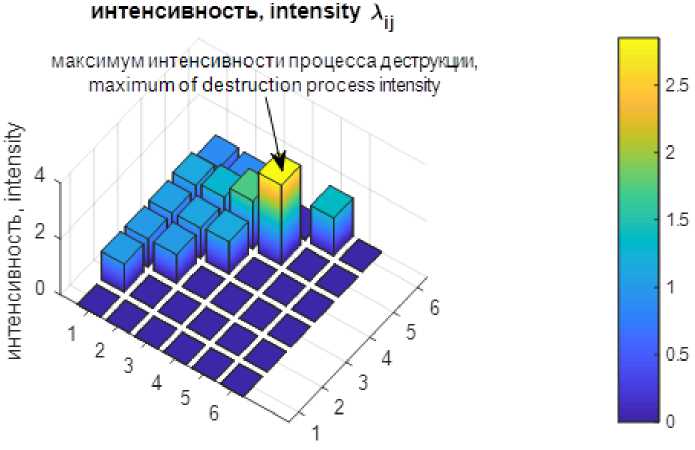
Визуализация найденной в ходе исследования матрицы интенсивности даёт наглядную картину интенсивности процесса деструкции для каждой фракции (рисунок 6), что существенно облегчает анализ процесса деструкции и позволяет в дальнейшем оптимизировать его с учетом фракционной динамики.

№ фракции, fraction number

№ фракции, fraction number

Рисунок 6. Визуализация матрицы интенсивности переходов λ _{i , j}

Figure6.Visualization of the intensity matrix of transitions λ _{i , j}

Все это позволяет использовать предложенную математическую модель для исследования процессов деструкции, отладки алгоритмов управления процессом и его оптимизации.