Синтез молибдата свинца PbMoO4 распылением Pb и Mo ионными пучками

Тонкие пленки молибдата свинца PbMoO4 являются весьма перспективными аку-стооптическими материалами. Среди существующих методов выращивания тонких пленок можно выделить метод распыления ионными пучками, который обладает рядом существенных преимуществ [1]. В частности, в данном методе рабочая камера отделена от пространства горения разряда, эксперимент проводится в условиях хорошего вакуума, ионным лучом можно управлять. В результате возможен рост тонких пленок без примесей, с воспроизводимыми свойствами.

В связи с этим исследование закономерностей роста тонких пленок молибдата свинца распылением ионными пучками представляет как научный, так и практический интерес.

В работе предложена методика выращивания тонких пленок молибдата свинца распылением двумя ионными пучками, а также проведен расчет коэффициентов распыления с помощью математической программы MathCad, что позволило определить оптимальные режимы ростовых процессов.

Результаты и обсуждение

В работе была использована установка с двумя ионными пучками [1]. В данной установке возможно осуществлять раздельное распыление двух мишеней двумя ионными пучками. В частности, выращивание тонких пленок молибдата свинца PbMoO4 может быть осуществлено распылением двух мишеней, одна из которых состоит из свинца Pb, а вторая — из молибдена Mo. Такое независимое распыление мишеней позволяет формировать стехиометрический состав газообразных потоков свинца и молибдена к подложке, что позволяет в последующем получать качественные пленки соединения. Предполагалось, что молибден и свинец по-разному распыляются под действием ионных пучков аргона. Следовательно, для каждой мишени необходимо подбирать разные энергии распыляющих ионов.

Такая методика вполне реализуема в данной установке. На рисунке 1 показана конструктивная схема установки с двумя ионными пучками.

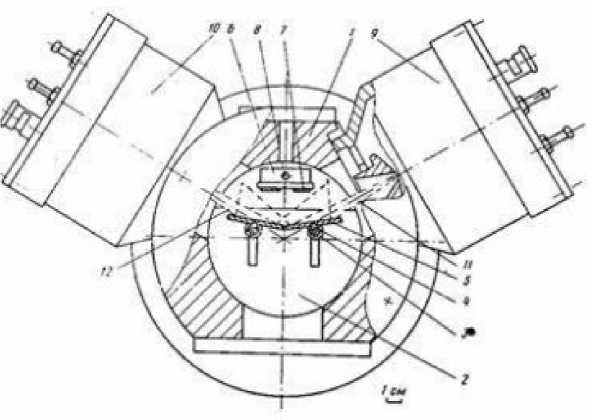
Рис. 1. Конструктивная схема установки с двумя ионными пучками: 1 — корпус;

2 — рабочая камера; 3 — стойка; 4 — держатели мишеней; 5 — мишени; 6 — держатели подложек; 7 — подложки; 8 — валик; 9, 10 — плазменные источники ионов;

11, 12 — пучки ионов аргона Ar+

С помощью математической программы MathCad были проведены расчеты, приближенные к реальному эксперименту. В данной работе были осуществлены расчеты по распылению мишеней из свинца и молибдена распылением ионными пучками аргона с введением формул и данных из теории Зигмунда [2]. Свинец и молибден в виде газообразных частиц поступают на поверхность подложки, последующий отжиг получившихся пленок на воздухе приводит к формированию тонких пленок молибдата свинца. Распыление осуществляется в результате каскадов атомных столкновений, подобно бильярдным шарам. Основной характеристикой процесса распыления является коэффициент распыления S, определяющий число выбитых атомов мишени одним падающим ионом (атом/ион). При расчетах учитывался угол падения ионов (углы в эксперименте были меньше 600):

s= ^s-^ . cosa Коэффициенты распыления рассчитывались по формуле Зигмунда:

s = 0,042 * a * ^, (2)

где α зависит от масс распыляющих ионов аргона М1 и масс распыляемых атомов мишени М2 свинца и молибдена; Sn(E) характеризует энергию упругого торможения ионов; Sn(ψ) — сечение ядерного торможения; U — энергия поверхност- ной связи. Поскольку определение энергии поверхностной связи весьма затруд- нительно, за U в вычислениях принимали энергию сублимации атомов мишени как наиболее близкий процесс.

Энергию упругого торможения иона аргона вычисляли по формуле: ^s_n(E} = 4n*Z₁*Z₂*e²* cr₁₂ * [ _(M^₂₎ ] * ^s_n⁽^⁾, где ^ = - ^{M 2 E} “ ¹² ₂ ; a₁₂ = 0,885 * a₀ * (Z f + ZT) ^ ;

(M₁+M₂)z₁z₂e² ’    ¹²     '          и ^{1     2}

S n (ψ) зависит от ψ и определяется экспериментально; а 0 — радиус Бора.

На рисунке 2 представлены зависимости коэффициентов распыления свинца и

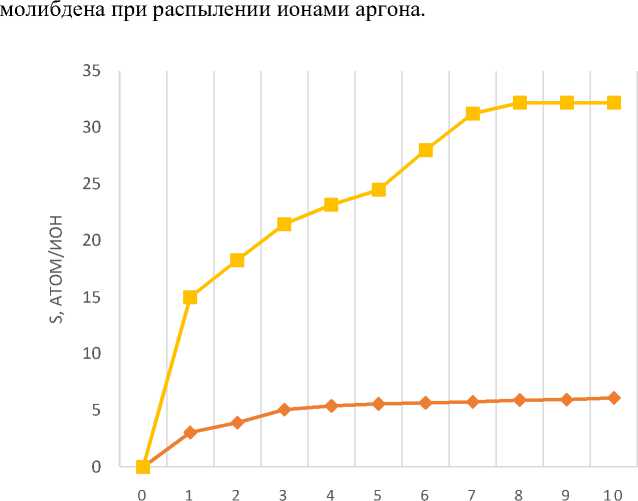
Е, КЭВ

Рис. 2. Зависимость коэффициентов распыления мишеней свинца Pb и молибдена Mo от энергии распыляющих ионов аргона Ar⁺ .

S (Mo)

S(Pb)

Результаты расчетов показали, что предлагаемая методика синтеза тонких пленок молибдата свинца путем первоначального распыления отдельно двумя пучками ионов аргона мишеней из свинца и молибдена, формирования потоков газообразных частиц свинца и молибдена по направлению к подложке, после- дующим отжигом в атмосфере полученных пленок приведет к формированию стехиометрических тонких пленок молибдата свинца.

Моделирование процессов распыления ионными пучками было проведено с помощью математической программы MathCad.

Расчеты приводят к выводу, что коэффициенты распыления свинца значительно превышают коэффициенты распыления молибдена. Следовательно, необходимо проводить корреляцию в энергии распыляющих ионов аргона для разных мишеней, что позволит определить оптимальные режимы ростовых процессов.