Синтез нейрорегуляторов для сложных технологических установок с применением бинарных нечетких отношений

• ¹ В связи с бурным развитием современных интеллектуальных технологий в отечественной и зарубежной промышленности приходится решать проблемы повышения эффективности работы систем управления

  © Буянкин В. М., 2013

сложными техническими установками. В системах управления сложными техническими установками довольно часто используются стандартные регуляторы: интегральный (И), интегрально пропорциональный (ПИ), интегрально пропорциональный дифференциальный (ПИД), которые широко зарекомендова-

HAVKO____________

Ж ГРАДА ли себя благодаря своей простоте и высокой надежности. Однако они не могут оперативно самообучаться и перестраиваться при изменении нелинейных параметров сложных элементов технических установок, особенно в случаях нечетких внешних возмущающих воздействий. Вместо этих регуляторов с жесткой структурой актуально использовать нейрорегуляторы на базе нейронных сетей, которые легко перестраиваются и переобучаются, изменяя свои коэффициенты и приспосабли-34 ваясь к внешней окружающей среде. Анализ работы большинства элементов технических установок сложен и не формализуем из-за неточности исходных данных. Многие характеристики невозможно измерить, например, параметры электрической дуги в ионно-плазменной установке, трение в электродвигателях, изменяющиеся во время работы моменты инерции. Поэтому для улучшения эффективности и качества управления актуально использовать нечеткую логику с мягкими вычислениями. Правильное сочетание нейронных сетей с нечеткой логикой позволяет получить необходимые статические и динамические характеристики систем управления сложных технических установок. Все это приводит к интеграции в нейроуправление нечетких интеллектуальных технологий.

Синтез систем управления с нечеткой логикой, выбирающей необходимую структуру нейрорегулятора для токового контура цифрового электропривода

В большинстве случаев сложная техническая установка с первоначальными параметрами по своим динамическим свойствам не удовлетворяет желаемым требованиям: она оказывается неустойчивой или имеет плохие показатели качества. Улучшение характеристик сложных технических установок может быть достигнуто при правильно сконструированном регуляторе. Регулятор – это один из наиболее важных функциональных элементов. Он обеспечивает необходимые динамические свойства – устойчивость, качество переходных процессов. От правильности выбора и выполнения регуляторов зависит в большинстве случаев работоспособность технологической установки. Выбор места включения, схемы и параметров регуляторов является одним из основных этапов синтеза. Динамические свойства элементов технических установок при классическом подходе математически вы-

№ 1 (3) январь-март 2013

ражаются передаточными функциями, полученными по экспериментальным частотным характеристикам. Используя стандартные классические теории синтеза систем автоматического управления, рассчитывают частотные характеристики регулятора. Традиционно на практике широко используются И (интегральные), ПИ (пропорциональные-интегральные), ПИД (пропорциональные-интегральные дифференциальные) регуляторы (рис. 1), которые хорошо и эффективно зарекомендовали себя для управления техническими установками с линеаризованными математическими моделями. Было разработано много методов настройки этих регуляторов. Наиболее распространенным является метод, основанный на данных работы технической установки при реакции единичного ступенчатого воздействия. Этот метод использовался достаточно продолжительное время и эффективно применяется инженерами-практиками и по сей день. Однако на современном этапе к сложным техническим установкам предъявляются все более высокие требования в отношении качества, эффективности и точности. Работу многих сложных технических установок невозможно описать системой линейных дифференциальных уравнений, рабочие точки статических и динамических характеристик из-за возмущений и существенных нелинейностей изменяются. Поэтому для обеспечения оптимальной настройки приходится вручную подбирать и перестраивать коэффициенты регуляторов. Оптимальная настройка в таких условиях становится невозможной, поскольку традиционные регуляторы не могут само-обучаться, особенно в условиях нечеткой информации, с неопределенными параметрами. Вместо традиционных регуляторов с жесткой структурой актуально использовать нейрорегуляторы на базе нейронных сетей, которые легко перестраиваются и переобучаются, изменяя свои коэффициенты, приспосабливаясь к внешней окружающей среде [1–3].

Для синтеза объектов регулирования с переменными нелинейными параметрами, представляющих собой одномассовые структуры, разработаны универсальные нейрорегуляторы первого и второго типов, обладающие интегральными и пропорциональными характеристиками (рис. 2).

Для синтеза объектов регулирования с переменными нелинейными параметрами, представляющих собой двухмассовые струк-

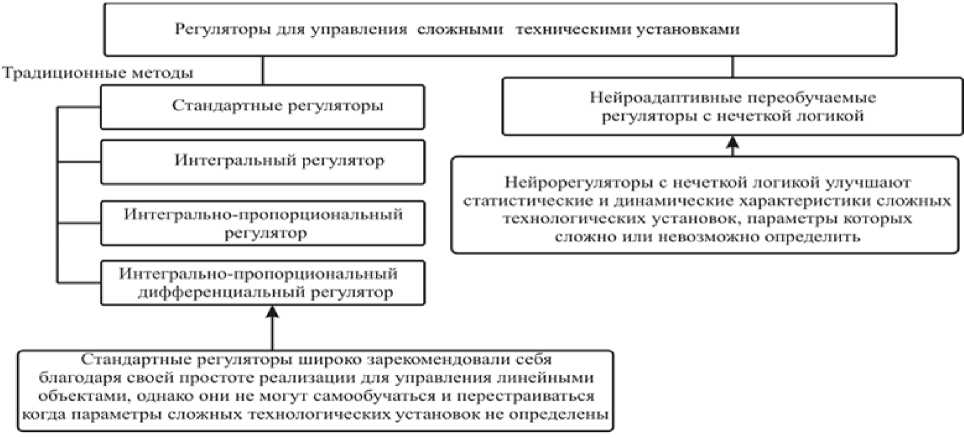
Рис. 1. Регуляторы для управления сложными техническими установками

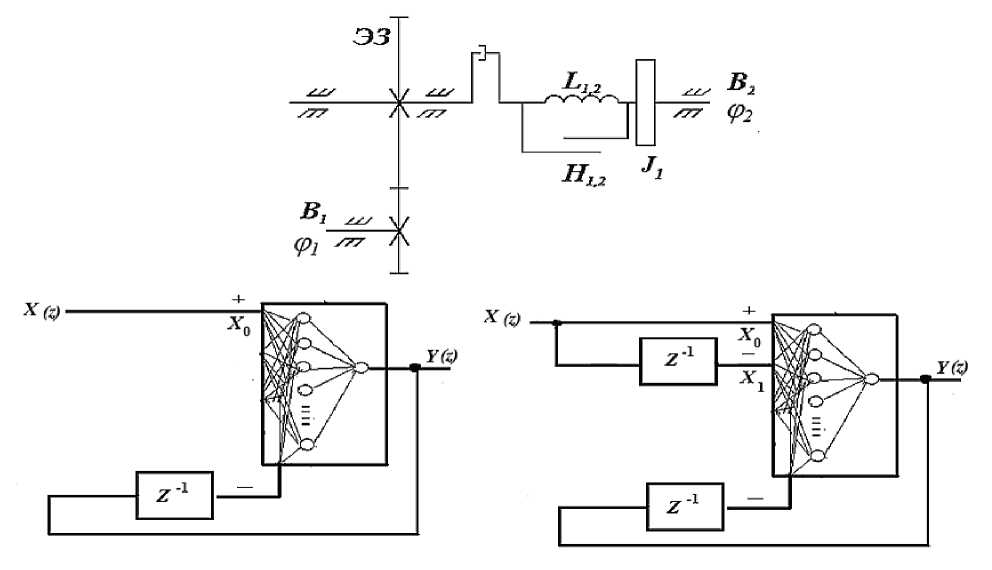
Рис. 2. Нейрорегуляторы первого и второго типов для синтеза одномассовых объектов регулирования

туры, разработан универсальный нейрорегулятор третьего типа, обладающий интегральными пропорциональными и дифференциальными характеристиками (рис. 3).

На рис. 2, 3 обозначено:

В 1, В 2, В 3 - входной и выходной валы;

Ф1, ф2, ф3 - углы поворота входного и выходного валов;

J 1, J ₂ - моменты инерции на выходном валу;

L ₁₃, L _2-3 – коэффициенты жесткости упругих ^, элементов;

Н 12 - коэффициенты демпфирования, характеризующий наличие внутренних сил вязкого трения в упругих элементах;

ЭЗ – безынерционный элемент зацепления с передаточным числом.

В представленных нейрорегуляторах элемент z осуществляет задержку сигнала на j шагов. На входы нейрорегуляторов подается n значений X ( z ) и m значений сигнала с выхода Y ( z ) .

HAVKO____________

Ж ГРАДА

Работа нейрорегуляторов с n количеством нейронов описывается системой уравнений:

X, = X₀*Z"',X₂ = X₀*Z"' Y^Y^Z"¹.

El = X0Wn-X1W12-X2W13-Y,Wl4;

Ei = X₀W₂₁ - X_xW_n - X₂W₂₃ - Y,W₂₄;

E₃ = X₀W₃₁ - Х^₃₂ - X₂W₃₃ - ^;

E = XW -XW -XW -YW •

^4 A0FK41 АГ K42 Л2КК43 /ГК44’

E„ = XtiW,lX-XxWn2-X2Wn3-YxWll4;

R, = tan szg(£,);                             (1)

R₂ = tan sig (£₂);

R₃ = tan sig (£₃);

R₄ = tan szg (£4);

R„ = tan sig (£„);

y₍; = ^iv^ /?₂w,'+ /г₃и<+ r₄w;+............r„w;,;

Уо = purelineYo, где Х0 – входной сигнал нейронной сети;

Y ₀ – выходной сигнал нейронной сети; Х ₁ = Х ₀ Z^{- 1} , Х ₂ = Х ₀ Z^{- 2} – входные сигналы

№ 1 (3) январь-март 2013

нейронной сети, задержанные на 1, 2 такта; Y ₁ = Y ₀ Z^{- 1} – выходной сигнал нейронной сети, задержанный на 1 такт; Е ₁… Е_т – выходные сигналы первого слоя нейронов; W ₁₁ …W_{n 4} – веса первого слоя нейронов; R ₁ …R_n – сигналы на выходе блоков активации первого слоя нейронов; Y ₀ ^’ – сигнал на выходе второго слоя нейронов; W ₁ ^’ …W_n ^’ – веса второго слоя нейронов; pureline – линейная функция активации.

Для решения задачи выбора необходимого типа нейрорегулятора, обеспечивающего требуемые статические и динамические характеристики работы сложных технических установок, используется модель, основанная на двух бинарных нечетких отношениях . Первое из этих нечетких множеств строится на двух базисных множествах X и Y , а второе – на двух базисных множествах Y и Z.

Множество X { J ₁, J ₂, R _я, L _я, H ₁₂, H ₂₃, L ₁₂, L ₂₃} описывает технологические параметры сложной технической установки:

R _я – сопротивление якоря электродвигателя;

L – индуктивность якоря электродвигателя.

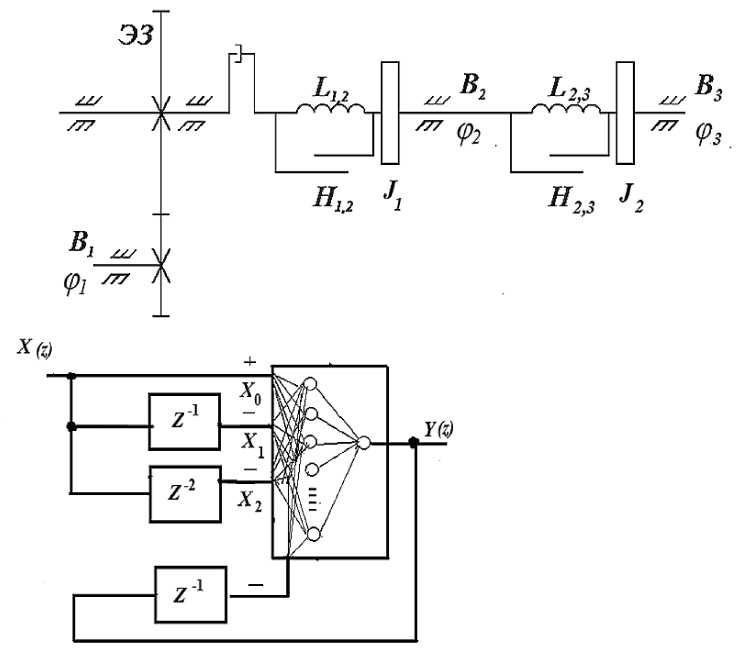
Рис. 3. Нейрорегулятор третьего типа для синтеза двухмассовых объектов регулирования

Множество Y { 0, n , 5, т } описывает технологические характеристики сложной технической установки:

• 0 - запас устойчивости;

• n - число колебаний переходного процесса;

• 5 - перерегулирование;

• т - длительность переходного процесса.

Множество Z { z 1, z ₂, z 3} описывает набор структурных схем нейрорегуляторов: нейрорегуляторы первого, второго, третьего типов.

На рис. 4 изображена функциональная схема блока вычисления max-min-свертки бинарных нечетких отношений.

Функция принадлежности max-min-свертки бинарных нечетких отношений Q, R вычисляется по формуле

И Q ® R ⁽ < x i , x k > ) =

• = max xi _c x { min { ц q ⁽ < x i , x j > ), ц r ⁽ < x i , x k > ) } } (2)

( V <  x i , x k >e Y x Z ).

При вводе параметров сложной технологической установки в блок вычисления maxmin-свертки бинарных нечетких отношений выбирается необходимый тип нейрорегулятора, который обеспечивает требуемое качество работы, соответствующее технологическим характеристикам.                               ³⁷

На рис. 5 изображена структурная схема с этапами синтеза и выбора адаптивных нейрорегуляторов на базе нейропрогнозирующей идентификации для систем управления сложными техническими установками с желаемы-

Технологические характеристики Y {0.11,5.Г }

е

п

Технологическне параметры

J г

R, - ^ - ^HV._ н^ —

L

Блок вычисления max-min свертки нечетких отношений

первый тип второй тип

третий тип

2{1\,1г,

Типы нейрорегуляторов

Х{ J\,Ji,R, ,L,,Hn,HB,Lxl }

Рис. 4. Функциональная схема блока вычисления max-min-свертки бинарных нечетких отношений

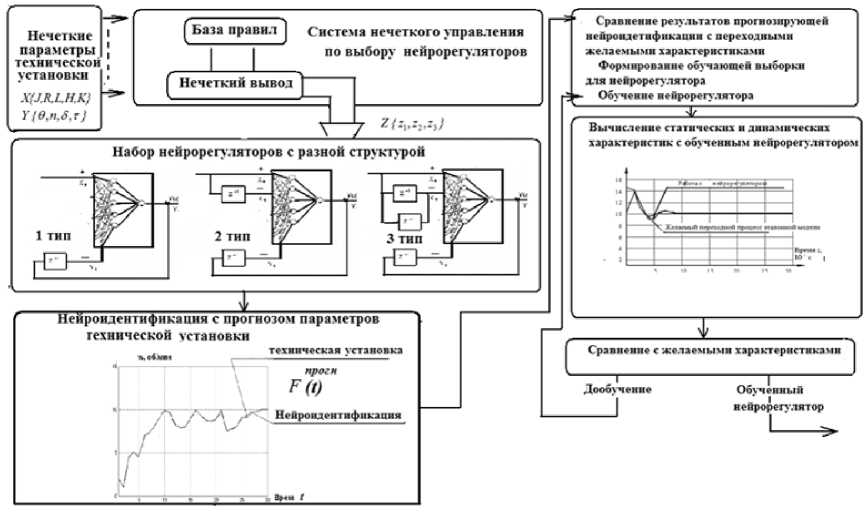
Рис. 5. Структурная схема синтеза адаптивных нейрорегуляторов на базе нейропрогнозирующей идентификации для систем управления сложными техническими установками с желаемыми характеристиками

HAVKO____________

Ограда ми характеристиками с применением нечетких интеллектуальных технологий.

Синтез нейрорегулятора состоит из этапов:

• 1)    выбора структуры нейрорегулятора с использованием нечетких параметров технической установки;

• 2)    нейроидентификации с прогнозом статических и динамических характеристик технической установки;

• 3)    сравнения результатов прогнозирующей 38 нейроидентификации с желаемыми переходными характеристиками;

• 4)    формирования обучающей выборки для нейрорегулятора;

• 5)    обучения нейрорегулятора;

• 6)    вычисления статических и динамических характеристиктехнической установкисобу-ченным нейрорегулятором;

• 7)    сравнений с желаемыми характеристиками эталонной модели.

Если необходимая точность управления сложной технической установкой не достигается, то проводится дообучение нейрорегулятора.

Работа адаптивного нейропрогнозируе-мого нейрорегулятора с эталонной моделью, имеющей желаемую характеристику сложной технической установки, описывается следующими уравнениями.

Уравнение эталонной модели

_ к=0                         /ОХ .(3)

Ъа^

1=0

Уравнение нейропрогноза

.

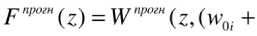
и7=1

Вычисление ошибки e_k ( z ):

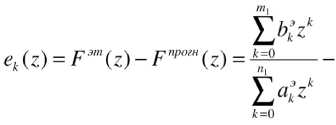
i=ij=i

Уравнения нейрорегулятора:

№ 1 (3) январь-март 2013

г^хл^^+УДз,

Е2=Х01У21-Х11У22+У11У2з

Е^ХЛ-^з+У,^

R^ = pureline^Ex\ r0 = W+............+r,X

Уо = purelineY0, где X0, Y0 - входной и выходной сигналы нейронной сети; X1, Y1 - входные сигналы нейронной сети, задержанные на один такт; E 1. En - выходные сигналы первого слоя нейронов; W... Wn3 - веса первого слоя нейронов; R j. Rn - сигналы на выходе блоков активации первого слоя нейронов; Y0 - сигнал на выходе второго слоя нейронов; W(... Wn - веса второго слоя нейронов; pureline - линейная функция активации.

Настройка нейрорегулятора осуществляется при условии

.            (7)

Эффективность данной методики была проверена на системе нейроуправления токовым контуром цифрового электропривода (рис. 6), смоделированной в среде MATLAB.

В структурной схеме:

• V A , V B , V C - напряжения трехфазного источника;

I з_ад, I я, I - ток задания, ток якоря электродвигателя, ток в обмотке возбуждения электродвигателя;

M _в, М – возмущающий момент, момент, развиваемый электродвигателем.

Структурная схема управления токовым контуром электропривода металлорежущего станка описывается системой нелинейных дифференциальных уравнений:

– уравнение обмотки

B В         в в

_ dt возбуждения;

– уравнение

Xi I             Xi xi          xl            •/ 1

at обмотки якоря;

J—^ = м-мн – уравнение моментов dt на валу электродвигателя;

Ф_в = k _Ф i _в, е _я = k_g ω _m Ф_в – уравнение ЭДС в обмотке возбуждения электродвигателя;

M = k _м i _я Ф_в – уравнение вращающего момента электродвигателя;

U_z = U_m (1 + cosα)/3,14 – уравнение тиристорного преобразователя,                (8)

где U _в – напряжение в обмотке возбуждения; i _в – ток возбуждения; r _в – активное сопротивление обмотки возбуждения; L _в – индуктивность обмотки возбуждения; Ф_в – магнитный поток обмотки возбуждения; U _я – напряжение на якоре; i _я – ток якоря; е _я – ЭДС якоря; r _я – активное сопротивление якоря; L _я – индуктивность якоря; J – момент инерции электродвигателя; ω – частота вращения электродвигателя; М – вращающий момент электродвигателя; М _н – момент нагрузки; k_g – коэффициент ЭДС электродвигателя; k_m – коэффициент момента электродвигателя; U_m – амплитудное значение напряжения; α – угол поджигания тиристоров.

В процессе работы многие параметры электропривода ( r _в, L _в, r _я, J ) изменяются по нелинейным зависимостям, поэтому использование традиционных классических регуляторов представляет большую сложность, так как они не обеспечивают необходимые статические и динамические характеристики.

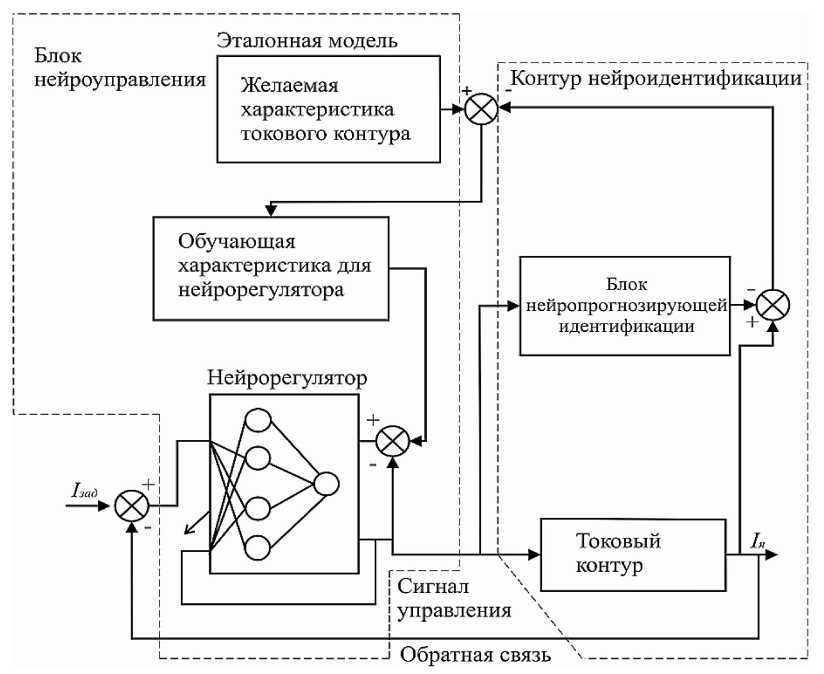
На рис. 7 представлена структурная схема контура нейросамонастройки с блоком нейропрогнозирующей идентификации. Контур нейросамонастройки состоит из эталонной модели с желаемыми характеристиками токо- вого контура [1, 6, 7, 9]. Желаемый выходной сигнал описывается следующим разностным уравнением:

I _{я gk} = Fg [ Iz_k + Izg_{k – 1} + Izg_{k – 2} + … + Izg_{k – n} ]. ( 9)

Структурная схема (рис. 7) состоит из контура нейроидентификации, где вычисляются и прогнозируются статические и динамические характеристики, и контура нейроуправления, где вырабатываются обучающие характеристики для нейрорегулятора, управляющего током электродвигателя согласно желаемым характеристикам эталонной модели. Данные блока прогнозирующей нейроидентификации сравниваются с данными эталонной модели, в результате сравнения получаются сигналы обучения для нейрорегулятора. Для обеспечения необходимых статических и динамических характеристик системой нечеткого управления выбран нейрорегулятор (рис. 8) с интегрально-пропорциональной структурой. Нейрорегулятор выполняет роль компенсации электромагнитной постоянной времени электродвигателя, что существенно увеличивает быстродействие токового контура.

При моделировании электропривода с переменными нелинейными параметрами было получено семейство обучающих характеристик для нейрорегулятора. В результате обучения нейрорегулятора и тестирования токового контура с нейросамонастройкой был получен переходный процесс, совпадающий с желаемым переходным процессом эталонной модели (рис. 8).

По переходным процессам, изображенным на рис. 8, можно сделать вывод, что си-

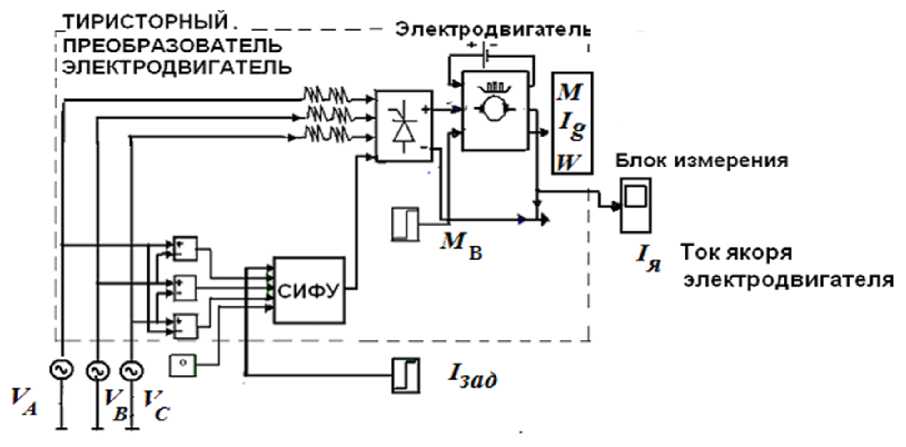
Рис. 6. Структурная схема управления токовым контуром цифрового электропривода, смоделированная в среде MATLAB

Havko-

Ограда

Нейрорегулятор

-| Обратная связь \

Эталонная модель

Блок нейроуправления

Обучающая характеристика для нейрорегулятора

Контур нейроидентификации

Желаемая характеристика токового контура

Блок н ейро пр о гн оз и ру ю щ ей иденти ф икаци и

Токовый контур

Сигнал управления

Рис. 7. Структурная схема контура нейросамонастройки с блоком нейропрогнозирующей идентификации

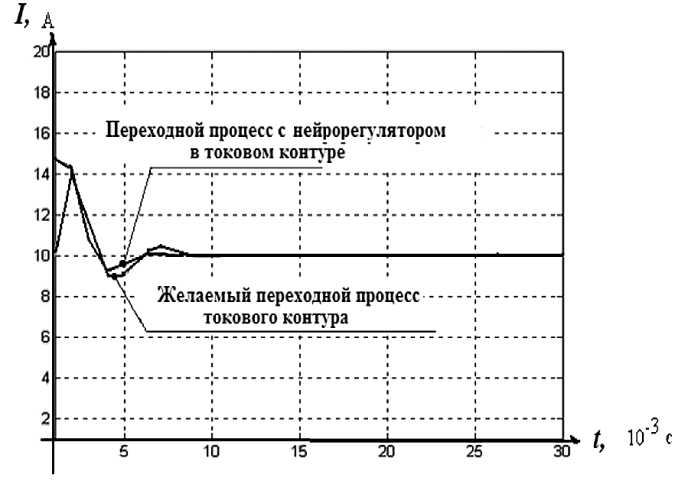
Рис. 8. Переходные процессы в токовом контуре с нейрорегулятором

стема нейроуправления с блоком прогнозирующей нейроидентификации обеспечивает необходимые желаемые статические и динамические характеристики токового контура электропривода.

Таким образом, разработанные методы синтеза нейроадаптивных нейрорегуляторов с использованием нечетких технологий с желаемыми характеристиками позволяют существенно повысить и улучшить статические и динамические параметры систем управления сложными техническими установками, что является на нынешний день важной и актуальной задачей.

Синтез нейрорегуляторов для сложных технологических установок