Синтез оптимального состава механизмов защиты путем решения задачи о назначениях в нейросетевом базисе нейронной сети Хопфилда

Выпуск 1/2019

В соответствии с принятой в Российской Федерации Доктриной информационной безопасности одной из основных задач национальной безопасности России является активное противоборство угрозам функционирования критически важных государственных информационных структур. Особое место в их перечне занимают механизмы защиты баз данных, обеспечивающие защиту хранимой информации в системах управления базами данных [2].

В стандартной постановке задачи существует множество уязвимостей, группируемых в уникальные группы и принимаемых как работы в задаче о назначениях (рис. 1). Наличие временных ограничений по скорости принятия решений на задействование тех или иных средств защиты входит в противоречие с размерностью задачи о назначениях.

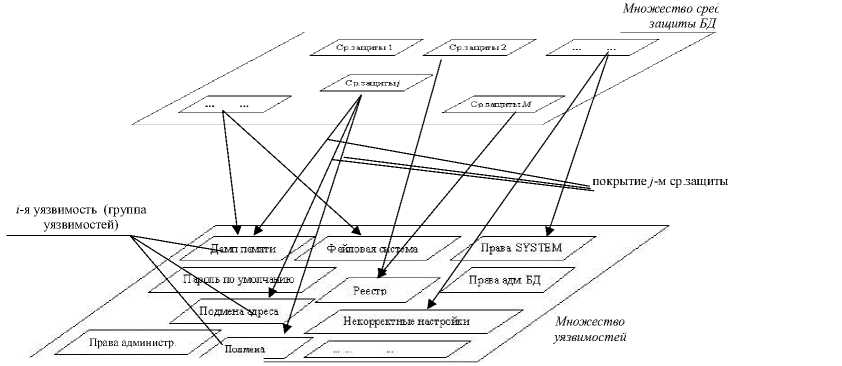
Множество средств защиты БД покрытие j-м ср .защиты i-я уязвимость (группа уязвимостей)

Права SYSTEM

Реестр

. П о дмена'эдре са

Некорректные настройки

Множество уязвимостей

Права администр.

Подмена

Рис. 1. Каждая группа уязвимостей БД представляется как i -я работа, j - е средство защиты БД представляется как j -й исполнитель

Пусть i -я группа уязвимостей состоит из k уязвимостей из N , где N – общее количество уязвимостей информационной системы. Число вариантов поочередного выбора к уязвимостей из N составляет N !/( N—k )!. В сформированных подмножествах из k уязвимостей каждая имеет свою определенную позицию. Однако от перестановок уязвимостей в покрываемом подмножестве номер соответствующего средства защиты не изменяется. Число подмножеств с различными мощностями составляет N . Поэтому максимальное количество групп уязвимостей (или работ в терминах задачи о назначениях)

N

n !

N max = ^ /к !( N - к ) к = 1

где N – общее количество уязвимостей БД или СУБД.

В связи с этим возникает необходимость в разработке эффективного алгоритма решения задачи о назначениях, к которой сводится задача синтеза оптимального состава механизмов защиты информационной системы [10].

Одним из математических аппаратов, позволяющих разработать высокоскоростной алгоритм, является аппарат теории динамических нейронных сетей Хопфилда.

Гладышев А.И., Буров Г.Г. Синтез оптимального состава механизмов...    141

В общем случае может быть рассмотрена нейронная сеть (рис. 2), содержащая произвольные обратные связи, по которым переданное возбуждение возвращается к данному нейрону, и он повторно выполняет свою функцию.

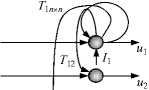
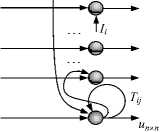
Рис. 2. Нейронная сеть Хопфилда – модель оптимизации при назначении средств защиты БД

Ответ на вопрос об устойчивости динамики произвольной системы с обратными связями крайне сложен и до настоящего времени является открытым. Дискретная сеть Хопфилда имеет один слой элементов (входные элементы, представляющие входной образец, не учитываются). Каждый элемент связывается со всеми другими элементами, но элемент не всегда связывается с самим собой [9]. За один шаг обновляется только один элемент, в отличие, например, от сети с обратным распространением ошибок, где все элементы слоя могут изменяться одновременно, если сеть реализована в виде аппаратных средств с соответствующими параллельными возможностями [5]. Элементы обновляются в случайном порядке, но в среднем каждый элемент должен обновляться в одной и той же мере. Например, в случае сети из 10 элементов после 100 обновлений каждый элемент должен обновиться приблизительно 10 раз. Вывод элемента ограничен значениями 0 или 1 (либо –1 или 1).

Изменение состояния каждого нейрона u_j в модели Хопфилда происходит по известному правилу для формальных нейронов Мак-Каллока и Питтса. Поступающие на его входы сигналы X_i в момент t взвешиваются с весами матрицы связей T_ij и суммируются, определяя полный уровень силы входного сигнала [6]:

h i = ∑ T ij u i .                                   (2)

i ≠ j

Далее в момент t + 1 нейрон изменяет состояние своего возбуждения в зависимости от уровня суммарного сигнала h и индивидуального порога каждого нейрона I :

U j ( t ⁺ 1 ) = - 1, h j ( t ) < I j.

* U j ⁽ t ^{+ 1 )} = ^{+ 1}, h j ⁽ t ) > I j ,                                  ⁽³⁾

U j ( t ⁺ 1 ) = U j ( t ) , h j ( t ) = I j .

Изменение состояний возбуждения всех нейронов может происходить одновременно, в этом случае говорят о параллельной динамике.

При обучении весовые значения для сети Хопфилда определяются непосредственно из учебных данных без необходимости проведения обучения в более привычном смысле. Сеть Хопфилда ведет себя как память, и процедура сохранения отдельного

142 Выпуск 1/2019

вектора представляет собой вычисление прямого произведения вектора с ним самим [1]. В результате этой процедуры создается матрица, задающая весовые значения для сети Хопфилда, в которой все диагональные элементы должны быть установлены равными нулю (поскольку диагональные элементы задают автосвязи элементов, а элементы сами с собой не связаны). Таким образом, весовая матрица, соответствующая сохранению вектора Х , задается формулой

T = X ^T X .                              (4)

При функционировании нейронной сети входной вектор задает начальные состояния всех элементов. Элемент для обновления выбирается случайным образом [12]. Выбранный элемент получает взвешенные сигналы от всех остальных элементов и изменяет свое состояние. Выбирается другой элемент, и процесс повторяется. Сеть достигает предела когда ни один из ее элементов, будучи выбранным для обновления, не меняет своего состояния [7].

Определим архитектуру нейронной сети, решающую следующую задачу:

f

У xj. < 1 i = 1 N, j=i

MNN

F (X) = У У rjiXji ^ max, при ограничениях: < У Xji < 1, j = 1,M,

• j=i i=i

x j. e { 0,1 } , j = 1 M , i = 1 N

Введем в рассмотрение сеть бинарных нейронов, представляющую собой матрицу размерностью n x n , где n = N = M - число средств защиты или групп уязвимостей. Требование бинарности нейронов не является обязательным и введено только из соображений наглядности и исходного соответствия значений параметров задачи и выходных сигналов бинарных нейронов. Каждой целочисленной переменной x_ij поставим в соответствие выходной сигнал j j -го нейрона u j. , стоящего в i -й строке и j -м столбце матрицы сети:

( X j = 1) О ( U j = 1), V i , j e l, n . (6)

На рисунке 3 схематично представлена матрица сети в состоянии покоя, где в виде заштрихованных квадратов изображены нейроны с единичными выходными сигналами Совокупность возбужденных нейронов интерпретируется как план назначений.

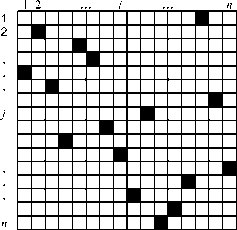
Рис. 3. План назначений – матрица нейронной сети Хопфилда в состоянии покоя

Гладышев А.И., Буров Г.Г. Синтез оптимального состава механизмов...    143

В соответствии с (6) интерпретируем ограничения и целевую функцию, в результате получаем                        _n

X u, = 1, V i е1, n; j=1 (7) n X ил = 1Vie1, n; (8) i=1 nn XX ъ=n; j=1 i=1 (9) nn ф(и) = XXииги ^ max, (10) j=1 i=1

где и . - значения выхода нейронной сети Хопфилда (см. рис. 2); j - значения матрицы производительности (табл.), элементы которой представляют собой эффективность средства защиты с номером j относительно уязвимости (группы уязвимостей) с номером i .

Задача о назначениях

	Уязвимость 1	Уязвимость...	Уязвимость i	Уязвимость...	Уязвимость N
Ср. защиты 1	r 11		r 1 i		r 1 N
Ср. защиты …
Ср. защиты j	rj 1		r ji
Ср. защиты …
Ср. защиты M	rM 1		rMj		rM N

Сконструируем энергетическую функцию E ⁰ ( и ), минимизация которой обеспечивает выполнение ограничений (7)–(9) и решение задачи (10). Построим ее в виде

E 0( u) = E U u) + E ф( и), где последнее слагаемое обеспечивает оптимизацию функции стоимости и с точностью до константы F > 0 однозначно определяется следующим образом [4]:

nn

E ф( и) = - F XX и„(12)

j = 1 i = 1

а первое слагаемое обеспечивает выполнение ограничений и может быть построено несколькими способами. Согласно первому из них данный компонент конструируемой энергетической функции имеет вид nnn      nnnnn

E К и) = у XXX V,. + 2 XXX и,и „ + Т (XX -  n) ■

• 2 j=1 I =1 VTI              2 I = 1 j=1 Ц* j              2 у j=1 i=1

где А, В и С - положительные константы.

Первое слагаемое принимает минимальное и равное нулю значение лишь в том случае, если каждая строка матрицы { u j } содержит не более одной единицы, второе слагаемое принимает минимальное нулевое значение, если каждый столбец данной матрицы содержит не более одной единицы, наконец, третье слагаемое принимает минимальное нулевое значение, если во всей матрице { и , } содержится ровно n единиц.

144 Выпуск 1/2019

То есть построенная функция E ° р ( и ) достигает своего минимума во всех состояниях, удовлетворяющих совокупности ограничений (7)–(9) и представляющих собой план назначений. Согласно второму способу построения данного компонента конструируемой энергетической функции будем иметь

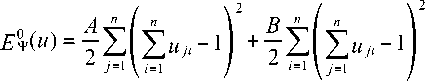
где первое слагаемое принимает минимальное нулевое значение только в том случае если в любой строке матрицы {и.} будет ровно один возбужденный нейрон, а второе -если в любом столбце этой матрицы будет ровно один возбужденный нейрон. В целом данная функция принимает минимальное нулевое значение только на состояниях удовлетворяющих ограничениям (7)–(8) и представляющих собой планы назначений.

Суммируя функцию (12) с функцией (13) или (14), сконструируем энергетическую функцию в завершенном виде:

nnn      nnn       _nn        nn

E ⁰( и ) = A ZZZ U j U j v + B ZZZ U ji U .- + C ( ZZ U ji - n ) - F ZZ U ji r ji , (15)

² j = 1 i = 1 v^ i             ² i = 1 j = 1 ц^ j            ² I j = 1 i = 1           /         j = 1 i = 1

или

( \ ²          /           \ ²

nnnnn

Z U ji - 1 + B Z Z U ji - 1 - F ZZ u ji r ji . i = 1           )     ² i = 1 \ j = 1          )        j = 1 i = 1

Определим параметры сети, сопоставив одну из полученных функций с энергетической функцией, записанной в общем виде:

nnnn

E ( u , T , I ) = - 1 ZZZZ T ² j = 1 i = 1 Ц= 1 V= 1

ji µν u ji u µν

nn

+ ZZ U ji i ji , j = 1 i = 1

где T_{ji μν} – коэффициент связи между входом ij -го нейрона и выходом μν -го; I_ji – смещение ij -го нейрона.

В данном выражении для энергетической функции сети умышленно опущен временной параметр в связи с тем, что при определении синапсов и внешних смещений он не играет какой-либо существенной роли как для сетей с дискретным временем, так и для сетей с непрерывным временем. Более того, данным выражением мы будем пользоваться при определении параметров синтезируемых сетей как с дискретными, так и с непрерывными состояниями. Основанием для этого служит тот факт, что энергетические функции сетей с дискретными и с непрерывными состояниями отличаются только наличием у последних интегрального слагаемого, которое ни от значений синапсов, ни от внешних смещений в явном виде не зависит [11].

Для того чтобы определить параметры сети в соответствии с построенной энергетической функцией, приведем выражение для этой функции к виду nnn

E °( u ) = A ZZZ U j U j v ² j =1 i =1 v^ i

nnn     nnnn

+ B zzz u j-i u .+ C zzzz U ji u hv

² i =1 j =1 h^ j           ² j =1 i =1 H=1 v=1

nn

— Cn YI uji j =1 i =1

nn

- F ZZ u ji r ji + Cn² i =1 /=1                ²

Гладышев А.И., Буров Г.Г. Синтез оптимального состава механизмов... 145

и приравняем коэффициенты при линейных и квадратичных членах последнего выражения и энергии (17). Последнее слагаемое из рассмотрения можно исключить, так как оно не зависит от состояния сети.

Сопоставление линейных членов позволит определить значения внешних смещений а сопоставление квадратичных членов даст возможность определить синаптические связи между нейронами [8].

Анализ первого слагаемого сконструированной энергетической функции свидетельствует о том, что любой нейрон сети должен иметь синаптические связи с коэффициентом –А со всеми нейронами одноименной с ним строки (условие μ = i ), кроме самого рассматриваемого нейрона (условие ν ≠ j ). Второе слагаемое диктует наличие связей с коэффициентом –В между нейронами одноименного столбца (условие ν = j ), кроме собственной обратной связи (условие μ ≠ i ). Третье слагаемое свидетельствует о том что все нейроны сети связаны друг с другом синапсами с коэффициентами –С . Воспользовавшись символом Кронекера δ _ji , запишем результирующее выражение для синаптических связей сети в виде

T ji ^v - ^- A 8 j _Ц (1 ^- 8 i v ) ^- B 8 i v (l — 8 j _ц ) ^- C ^-

• ^{- -} A 8 j ц ^- B 8 i v ^{+ (} A ⁺ B ) 8 j _ц8 i v - C , i , j , ^ ^{, VG} 1, n •             ⁽¹⁹⁾

Анализ четвертого и пятого слагаемых сконструированной энергетической функции свидетельствует о том, что на все нейроны сети необходимо подавать внешние смещения в виде

I ji - — Cn — FC ji , i , j e 1, n .                       (20)

Как правило, в практических задачах принимают F = 1 и А = В , тогда все ненулевые связи имеют одинаковый вес, равный –A . Кроме того, анализируя выражения (19) и (20), можно заметить, что наличие глобальных связей с коэффициентом –С каждого нейрона с каждым в конечном состоянии сети, соответствующем некоторому плану назначений, обеспечивает подачу на любой нейрон со стороны всех других суммарного сигнала, равного –Сn , который компенсируется постоянным смещением –Сn . Следовательно, для упрощения структуры синапсов сети глобальными связями с весом –С и смещения –Сn в первом приближении можно пренебречь [3]. В этом случае упрощенную структуру сети для синтеза оптимального состава механизмов защиты путем решения задачи о назначениях можно представить в виде, изображенном на рисунке 4.

Группы уязвимостей

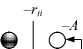
j _{– A}

n

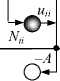
ОО

–

О

1     2 … i … n

Рис. 4. Динамическая нейронная сеть, релаксирующая к своему энергетическому минимуму интерпретированному в качестве оптимального состава механизмов защиты