Синтез оптимальных дифференциаторов для алгоритма обнаружения локально ориентированных текстур

Обнаружение областей с локально ориентированными текстурами является важным этапом в различных задачах анализа изображений слоистых структур земной коры [1], отпечатков пальцев [2, 3], следов от инструментов взлома [4], дефектов в виде трещин [5] и т.п. Обнаружение заключается в том, чтобы на основе анализа фрагмента изображения решить, принадлежит ли он информативной анизотропной области (локально ориентированной текстуре) или изотропному фону. При этом возможны два вида ошибок. Первый вид ошибок состоит в принятии решения о том, что анализируемый фрагмент является анизотропным, когда в действительности он является изотропным. Второй вид ошибок состоит в принятии анизотропного фрагмента за изотропный. Далее эти ошибки по аналогии с терминологией, принятой в математической статистике, будем называть ошибками первого и второго рода, обозначив соответственно а и р .

В большинстве практических случаев функция яркости локально ориентированной текстуры в пределах области малых размеров может быть аппроксимирована детерминированной полигармонической функцией, изолинии которой представляют собой параллельные прямые [3, 6, 7], проходящие под углом у к оси абсцисс:

z = ^{ z ( i , , i 2 ) =

= z ( i , cos у + i ₂ sin y ); i , = - n , n , i ₂ = - n , n }, где

z ⁽ i , , i 2 ) =

L

= ^ A, cos ( 2 n ( Q li , cos y + Q li ₂ sin y ) + ф l ) .

1 = 1

В (1) и (2) частоты Ql образуют возрастающую последовательность 0 < Q, < Q2... < QL < 0,5 , начальные фазы фl и амплитуды Al - произвольные неслучайные величины, (2n +,) х (2n +,) = N х N - размер анализируемого фрагмента, угол у является случайной величиной. При отсутствии априорной информации о преимущественных направлениях ориентации анизотропной текстуры распределение угла y обычно полагают равномерным на интервале

( -

п п

2,2].

Двумерные сигналы (1) обладают свойством локальной линейной симметрии (ЛЛC; local linear symmetry) [6]. Для их обнаружения широко применяются алгоритмы на основе градиентного структурного тензора (ГСТ) [6, 7], использующие масочные дифференцирующие фильтры (МДФ) для вычисления производных по вертикальному и горизонтальному направлениям дискретных двумерных сигналов. Поскольку цифровые изображения заданы на дискретной решётке, которая является анизотропной, то оценки ориентации имеют значительное смещение [7, 8]. Для снижения уровня систематической ошибки в [7] предложено использовать оптимизированные МДФ, аппроксимирующие идеальные дифференциаторы с высокой точностью. В [9] предложен способ построения МДФ, минимизирующих уровень систематических ошибок исходя из спектрально-корреляционных свойств локально ориентированных текстур.

Но существенно более важным для алгоритма обнаружения является синтез МДФ на основе минимизации ошибок обнаружения. В [10] получены соотношения для вычисления вероятности ошибки только первого рода на основе метода главных компонент при условии, что поля производных изотропного фона по вертикальному и горизонтальному направлениям являются статистически независимыми дискретными гауссовскими белыми шумами. В [11] вероятность ошибки первого рода вычисляется на основе анализа спектральных моментов при аналогичных условиях. Применение этих методов ограничено тем, что производные по направле- нию даже для дискретного белого шума являются коррелированными случайными последовательностями. Кроме того, методы вычисления вероятности ошибки второго рода отсутствуют.

Целью работы является разработка метода построения оптимальных помехоустойчивых МДФ, учитывающего влияние шума наблюдения, свойства и размеры анализируемого фрагмента анизотропной текстуры на вероятности ошибок алгоритма обнаружения на основе ГСТ.

1. Алгоритм обнаружения на основе ГСТ

Обозначим через H ₀ гипотезу о том, что анализируемый фрагмент λ является изотропным фоном, а через H ₁ – гипотезу о том, что λ является анизотропной текстурой (1), наблюдаемой на фоне аддитивного шума:

Ho' x = П о ,                                       (3)

H 1 ' X = z + П 1 ,                                    (4)

где

П о = { П о ( i i , i 2 ), i = - n , n , i 2 = - n , n}

и

П 1 = H( i i , i 2 ), i i = - n , n , i 2 = - n , n}

– дискретные гауссовские белые шумы с нулевыми математическими ожиданиями и дисперсиями D _η ⁽⁰⁾ и D _η ⁽¹⁾ соответственно.

Если мера анизотропности [6,7]

J J2 + J²

X ( J ) = ^{V 1    2} <  C ,                            (5)

J ₃

то принимается решение о том, что истинной является гипотеза H ₀ , в противном случае принимается решение об истинности гипотезы H ₁ , где

J ₁

J    J 2

J ₃

nn

2 EE K i ( fi , f 2 ) G x ( f , f 2 )

k i =- n k 2 = i

= 2

nn

EE к 2( fi, f2) gx (fi, f2)+ ki =-n k2 =i

n

+ E K 2( fi ,0) G x (fi ,0) ki=i nn

E E к з ( f i , f 2 ) g x ( f i , f 2 )

k i =- n k 2 = i

n

+ E к з ( f i ,0) G X ( fi ,0) k i = i

– вектор компонент ГСТ;

G x ( f i , f 2 ) = _y | S x ( f i , f 2 )|                           (7)

– выборочный двумерный спектр мощности фрагмента λ ;

S _λ ( f ₁, f ₂) – двумерный спектр этого же фрагмента, вычисленный с помощью дискретного преобразования Фурье;

k f = —i-, i = i, 2 - пространственные частоты;

iN

K i ( fi , f 2 ) = K x ( fi , f 2 ) ^( f , f 2 ),

K 2 ( f , f 2 ) = | K x ( f , f 2 )| ² - IK y ( f , f 2 )| ² ,

K з ( f , f 2 ) = | K x ( f , f 2 ) I ² + | K y ( f , f 2 ) I ²

• – двумерные весовые функции;

• 2. МДФ с разделимыми КЧХ

K_x ( f ₁, f ₂) и K_y ( f ₁, f ₂) – комплексные частотные характеристики (КЧХ) МДФ, дифференцирующих двумерную функцию яркости соответственно вдоль строк и столбцов дискретного изображения;

C – порог, принимающий значения от 0 до 1 , поскольку мера анизотропности 0 < x ( J ) <  i; для изотропного поля x ( J ) = 0, а для текстуры с ЛЛС при отсутствии шума x ( J ) = i [6, 7].

В (6) учтено свойство симметрии спектра мощности G _λ ( f ₁, f ₂)и то, что весовая функция K ₁( f ₁, f ₂) равна произведению КЧХ K_x ( f ₁, f ₂) и комплексно сопряжённой КЧХ K_y ( f ₁, f ₂) дифференцирующих фильтров. Кроме того, следует отметить, что мера анизотропности (5) инвариантна к значению дисперсии шума D _η ⁽⁰⁾ .

По аналогии с помехоустойчивым оператором Собела будем строить помехоустойчивые МДФ размером W х W = (2 w + 1) х (2 w + 1) элементов в классе разделимых фильтров, сглаживающих изображение в направлении перпендикулярном дифференцированию:

K x ( f i , f 2 ) = S( f i ) D( f 2 ),                          (8)

K y ( f , f 2 ) = D( f )S( f 2 ),                       (9)

где КЧХ дифференцирующего и сглаживающего масочных одномерных фильтров соответственно равны [7] :

w

®( f ) = 2 j (sin(2 n f ) + E d k sin(2 n kf )),        (i0)

k = 2

w

5( f ) = i + 2 E ^i cos(2 n kf );                  (ii)

k=i d = {dk, k = 2, w} и s = {sk, i = i, w} - весовые коэффициенты одномерных фильтров c конечными им- пульсными характеристиками размером W = 2w +1 элементов;

j – мнимая единица.

Поскольку величина решающей статистики х ( J ) не изменится при умножении КЧХ одномерных фильтров S( f ) и S( f ) на произвольную положительную константу, то, не нарушая общности, в (10) и (11) принято, что (( = 1 и У 0 = 1.

• 3.    Критерий оптимизации

При анализе изображений информация об априорных вероятностях гипотез H ₀ и H ₁ обычно отсутствует, поэтому будем полагать распределение гипотез равновероятным. Оптимальные значения коэффициентов d , s и порога C определим путём минимизации вероятности ошибки P :

P m = min P ,                               (12)

d,s,C где

P = ( а + в )/2.                            (13)

В (13) учтено, что вероятность ошибки первого рода не зависит от параметра у . Вероятность ошибки второго рода зависит от у , так как сетка отсчётов и квадратная область, на которой задана анизотропная текстура, являются также анизотропными. Поскольку в алгоритме обнаружения значения коэффициентов d , s и порога C не должны зависеть от неизвестного параметра у , то в (13) используется усреднённая вероятность ошибки второго рода:

• 1    п/2

в = - f e ( Y ) d Y .                              (14)

^П ■' :

гипотеза H_r и при фиксированном значении пара-

метра y ■

Вероятности ошибок первого и второго рода для (5) равны:

а = 1 -

MM    M

P(y) =

MM    M

=JJ J

-M

-M

k

N 3 ( m ⁽⁰⁾ , R ⁽⁰⁾ | H o )d J з d J , d J 2 ,

J

V ( J 1² + J 2² )/ C ²

N ₃( m ⁽¹⁾ , R ⁽¹⁾ | H 1 )d J ₃ d J 1 d J ₂.

J

Используя свойства числовых характеристик статистически независимых случайных величин, условные математические ожидания (15) и компоненты условных ковариационных матриц (16) c учётом (6) можно представить в виде:

m

( r ) =

= 2

nn

2 ZZK1(f, f2)M{GXr)(f, f2)} kJ =-n k2 =1

nn

ZZ K 2 ( f , f 2 ) M { G x r ) ( f , f 2 )} + k 1 =- n k 2 = 1

n

+ Z K 2 ( f ,0) M { G x r ) ( f ,0)} k 1 = 1

nn

Z Z K 3 ( f , f 2 ) M { G x r ) ( f , f 2 )} k 1 =- n k 2 = 1

n

+ Z K 3 ( f ,0) M { G x r ) ( f ,0)} k 1 = 1

4. Параметры условных распределений компонент вектора J

Для гипотез (3) и (4) компоненты вектора (6) представляют собой взвешенные суммы статистически независимых отсчётов двумерного дискретного спектра мощности    G _λ ( f ₁, f ₂) . Поэтому при

N ² >  70 - 80 условные трёхмерные распределения вектора J можно считать приближённо гауссовскими: N ₃( m ⁽⁰⁾ , R ⁽⁰⁾ | H ₀) и N ₃( m ⁽¹⁾ , R ⁽¹⁾ | H ₁) , где

m ^{( r} ) = ^ m{^r )

и

m 2 ^r ) m 3 ^r ) J ; r = 0,1

R ⁽ r ) =

( r ) 11

( r )

R ₁₂

( r ) R ₁₃

( r ) R ₁₂

( r ) R ₂₂

( r ) R ₂₃

( r ) R ₁₃

( r ) R ₂₃

( r ) R ₃₃

; r = 0,1

nn

^ 1⁽2 r ) = 8 Z Z K 1 ( f , f 2 ) K 2 ( f , f 2 ) D{G x r ) ( f , f 2 )}, k ₁ =- n k 2 = 1

nn

R (3 ) = 8 Z Z K 1 ( f , f 2 ) K 3 ( f , f 2 ) D { G X r ) ( f , f 2 )}, k 1 =- n k 2 = 1

R 2 ₃ ^{r )} = 4 X

I n n x| Z Z K 2 ( f1, f2 ) K3 ( f1 , f2 ) D { GXГ) ( f , f2 )} + k k]=- n k2 =1

n                                                    1

+ Z K2 (f ,0) K3 (f ,0) D {GXr) (f1,0)} I, j1=1                                                        J

I n n r2;)=4| ZZk2(f1,f2) d{gxr)(f1,f2)}+ k k1=- n k2 =1

^1

+ Z K2 (f ,0) D {Gxr) (f ,0)} I, j1=1                                          J

– математические ожидания и ковариационные матрицы вектора J при условии, что истинной является

I n n

R 33) = 4 ZZ K 3 ( f i , f 2 ) D { G i r ) ( f i , f 2 ) } +

I k J =- n k 2 = 1

n

+ Z K3 (f ,0) D {G^r) (f ,0)} ji =1

свойств гауссовского распределения, математическое ожидание и дисперсия отсчётов выборочного двумерного спектра мощности для гипотезы H ₁ равны:

r = 0,1, где M{Gλ(r)(f1, f2)} и D{Gλ(r) (f1, f2)} - математические ожидания и дисперсии статистически независимых отсчётов выборочного двумерного спектра мощности фрагмента λ при условии, что истинной является гипотеза Hr и при фиксированном значении параметра у .

Для гипотезы H ₁ из (4) и (7) следует, что

G (1) ( f , f 2 ) = G z ( f , f 2 ) + G П ¹) ( f , f 2 ) +

+ N(Re Sz (f, f2) Re S™(f, f2)+

+ Im Sz (f, f2) Im S« (f, f2)), где

Gz (f, f2) = ^ Sz (f, f2)|2,(21)

GП1)( f, f2) = n't |S™( f, f^

– выборочные двумерные спектры мощности анизотропной текстуры z и аддитивного шума η ₁ ; Re S z ( f 1 , f 2 ), Re S η ⁽¹⁾ ( f 1 , f 2 ) и Im S z ( f 1 , f 2 ), Im S _η ⁽¹⁾ ( f ₁ , f ₂ ) – действительные и мнимые части выборочных двумерных спектров S _z ( f ₁, f ₂) и S _η ⁽¹⁾ ( f ₁, f ₂) соответственно.

Используя свойства преобразования Фурье, нетрудно показать, что спектр дискретного полигар-монического сигнала (1) равен:

S z ( f , f 2 ) =

= j Z A ( * ( f -Q । , . , f 2 -Q । , c ) exP ( j Ф । ) +      (23)

⁺ ^ ( f i ^{+ Q} l , s , ^f 2 ^{+ Q} l,c ) exP (^{- j} Ф l ) ) ,

M { G Г’ С f i , f 2 )} = G z ( f i , f 2 ) + D ™,               (24)

D { G (1) ( f i , f 2 )} =

2 D П ¹) ( D ; ¹) + G z ( 0,0 ) ) , f i = f 2 = 0;             (25)

D¹^¹ ( D n i'¹ + 2 G _z ( f i , f 2 ) ) в остальных случаях.

Приравняв нулю G _z ( f ₁ , f ₂ ) и заменив D _η ⁽¹⁾ на D _η ⁽⁰⁾ , получим аналогичные соотношения для гипотезы H ₀ :

M { G Г( f i , f 2 )} = D Г                     (26)

D { G < ⁰⁾ ( f i , f 2 ) } =

= j 2 ( D^ ) ² , f i = f 2 = 0;                        (27)

l ( D ПП 0) ) , в остальных случаях.

5. Результаты экспериментальных исследований

Синтез МДФ проводился для анизотропной текстуры

z ( i ), i ₂) = A Z cos(2 n ( Q _li_i cos у + Q _li ₂ sin Y ))     (28)

l = i

при Q ' = 0,i5 и Q ₂ = 0,2

Вероятности ошибок a , Р ( у ) и в в соответствии с (17), (18) и (14) определялись численным интегрированием. Для поиска оптимальных значений коэффициентов d , s и порога C , удовлетворяющих критерию (12), использовались стандартные

методы оптимизации.

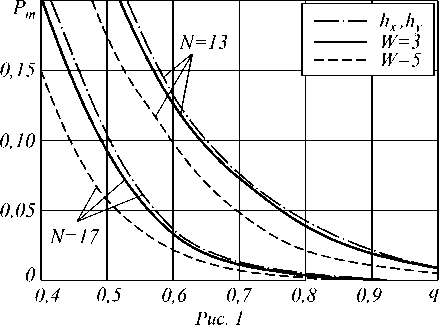
На рис. 1 приведены зависимости вероятности

ошибки P от отношения сигнал/шум q = .     , m                                          2Dη(1)

где

где

Q _l s = Q _l sin у ; Q _lc = Q _l cos у ;

0,3 0 - 0,3

h x

= h T

- 1

* ( f, f =    li^ in ^ f;^

N = 1 sin n f i

– нормированная час-

тотная характеристика двумерного прямоугольного окна с единичными весовыми коэффициентами [12].

Отсчёты действительной и мнимой частей дискретного спектра белого гауссовского шума S _η ⁽¹⁾ ( f ₁ , f ₂ ) являются гауссовскими статистически независимыми случайными величинами с нулевыми математическими ожиданиями. С учётом (20) и

0,3 0 - 0,3

– нормированные импульсные характеристики МДФ, полученные в [7] с целью минимизации систематической ошибки оценивания ориентации алгоритмом на основе ГСТ; 2 A / 2 – эффективное значение полигармонического двумерного сигнала (28).

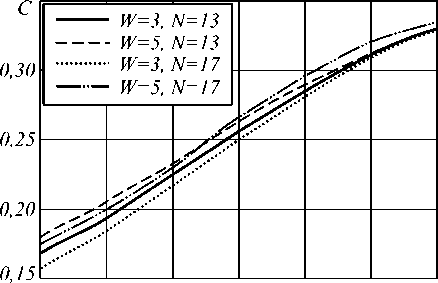
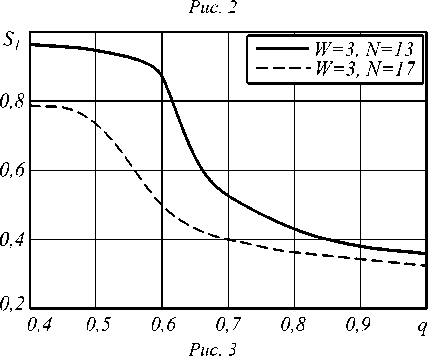
На рис. 2 и рис. 3 приведены зависимости оптимальных значений порога C и весового коэффициента jj МДФ размером 3 х 3 от отношения сиг-

нал/шум. Отметим, что в (29) весовой коэффициент j = 0,3 .

Поскольку предложенный метод синтеза является приближённым, то эффективность оптимальных дифференциаторов проверялась методом компьютерного моделирования. Оценка вероятности ошибки обнаружения P_m ^* вычислялась путём усреднения по 10 ⁵ тестовым изображениям для каждого значения отношения сигнал/шум q при независимых реализациях аддитивного дискретного белого гауссовского шума от изображения к изображению. Значение у в (28) менялось случайным образом от изображения к изображению в соответствии с равномерным распределением в диапазоне ( -л/ 2,л/2].

0,4    0,5     0,6    0,7    0,8    0,9 q

На рис. 4 приведены зависимости вероятности ошибки обнаружения от q , полученные путём ап-

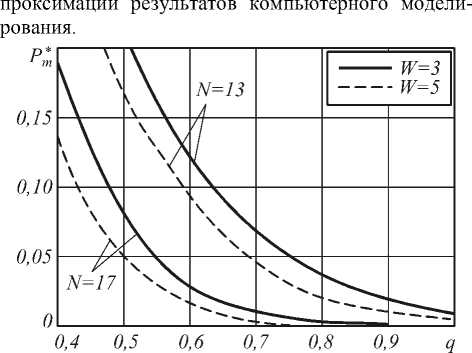
Рис. 4

По результатам проведённых исследований можно сделать следующие выводы.

• •    Использование оптимальных МДФ обеспечивает уменьшение вероятности ошибки обнаружения более чем на 5% для маски размером 3 х 3 и более чем на 20% для маски размером 5 х 5 по сравнению с МДФ, предложенным в [7].

• •    Значение порога C увеличивается при увеличении отношения сигнал/шум и слабо зависит от размеров анализируемого фрагмента и МДФ.

• •    При q <  1 помехоустойчивый оптимальный МДФ размером 3 х 3 значительно отличается от МДФ (29).

• •    Рассчитанные значения вероятностей ошибок алгоритма обнаружения хорошо согласуются с результатами компьютерного моделирования .

Заключение

В работе предложен метод синтеза оптимальных масочных дифференцирующих фильтров, минимизирующих вероятность ошибки алгоритма обнаружения локально ориентированных текстур на основе ГСТ. Метод основан на гауссовской аппроксимации совместного распределения компонент ГСТ. Отличительной особенностью метода является учёт шумов, искажающих анализируемую текстуру. Результаты экспериментальных исследований показали, что помехоустойчивые оптимальные МДФ отличаются от известных в литературе дифференциаторов.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант № 11-07-00077-а) .