Синтез программного и финитного законов движений в аналитических моделях управления конечным состоянием биомеханических систем

Аналитический синтез управляющих воздействий спортсмена целесообразно рассмат- ривать с позиций теории автоматического управления (ТАУ), моделирования [1, 6, 7, 14, 16, 17] и робототехники [3, 15, 19, 20, 22]. В ТАУ выделяют такие виды управления, как программное и финитное [13, 18, 21].

В соответствии с терминологией, принятой в теории управления [18, с. 18]: «Финитное управление (Fixed-timecontrol) – управление, цель которого заключается в переводе объекта управления из заданного начального состояния в заданное конечное состояние за ограниченное время». Здесь время процесса перемещения объекта заранее указывается, а начальное и конечное состояние объекта регламентируется его координатами.

Определение программного управления

(Programmedcontrol) следует из источника [18, с. 18]: «Управление, при котором значения управляющих и (или) управляемых координат изменяются в соответствии с заданной программой».

В настоящем исследовании биомеханиче- ская система рассматривается как материаль- ная точка, за которую можно принять, например [9], общий центр масс биосистемы, а также суставы опорно-двигательного аппарата тела человека, центр масс сегментов и т. п.

В работе [2] выделяются следующие виды движений, для которых выполняется синтез программного и финитного управления на уровне материальной точки: разгон, приведе- ние, разомкнутое по времени сближение, замкнутое по времени сближение. В рамках настоящей статьи рассматривается алгоритм синтеза программного и финитного управлений для биомеханической системы, совершающей разгон, что и актуализирует тему исследования.

Результаты исследования. Алгоритм синтеза программного и финитного управлений для биомеханической системы . Введем обозначения для фазовых координат биомеханической системы (материальная точка):

S0 – начальное фазовое состояние объекта движения по координате;

V 0 – начальное фазовое состояние объекта движения по скорости;

Sk – конечное фазовое состояние объекта движения по координате;

Vk – конечное фазовое состояние объекта движения по скорости.

Соответственно: u = V, V, S - ускорение, скорость и перемещение объекта управления.

Сформулируем задачу управления. Пусть известны параметры начального фазового состояния объекта управления по скорости [ V 0 ]. Требуется за время T перевести объект в конечное фазовое состояние [ V k ].

Известный программный закон управления, разомкнутый по управляемой фазовой координате V [2, с. 18], для модели разгона материальной точки представим в следующем виде:

V = V o + VT t, при t G [ T o ; T o + T ]. (1)

Из (1) следует, что постоянное ускорение ( u ) равно

V u = —

V 0

T

.

Если текущее фазовое состояние объекта считать начальным, то, заменив V 0 в (2) на текущую скорость V , а заданное время разгона T соответственно на оставшееся время T – t , получим закон управления с обратной связью [2]

u =

V k - V T - t "

Здесь t отсчитывается с момента времени начала разгона. Из (3) следует, что в момент времени t = T знаменатель уравнения превращается в нуль, т. е. в конечный момент времени уравнение (3) имеет особенность. Один из способов устранения особенности, предложенный в [1], заключается в том, что (3)

приводится к виду u = k0 + k1t + kvV,

где k = Vk — Vo + V^. k = Vk — Vo ; 0 T A T ; 1 TA T ;

kv =- —, v A T

A T - малая величина времени. V - текущая скорость объекта движения; t – текущее время (G <  t <  T ).

Абсолютная величина A T, трактуемая как «жесткость управления» [2], обычно составляет 0,03 T – 0,05 T (с). Текущая скорость ( V ) определяется из уравнения

V = ( V o* - V o )e ^- t/ ^{A T} + V , + V k TV^t . (5)

Здесь V ₀^* – действительное фазовое состояние объекта при t = 0, отличающееся от программного начального состояния V 0 , которое принято при расчете программы движения.

Уравнения (4)–(5) не предоставляют полной картины о движении объекта, так как отсутствуют аналитические зависимости, описывающие эволюцию траектории объекта. Поэтому в своих исследованиях мы использовали метод численного интегрирования, реализация которого приведена в работах [8, 12]. Дважды интегрируя u из (4), получаем на каждом шаге интегрирования скорость ( V ) и координату ( S ) объекта движения.

Компьютерная реализация алгоритма программного и финитного закона управлений. Авторская разработка компьютерного обеспечения темы статьи реализована в языковой среде Visual Basic 2010 [11] на базе интегрированной среды разработки Visual Studio Express 2013 под управлением Windows. В ка-

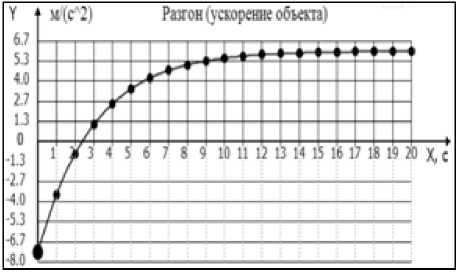
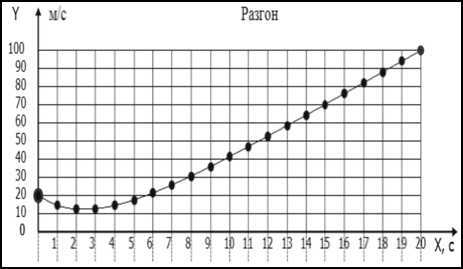
Ускорение [ и ]                                      Скорость [ V]

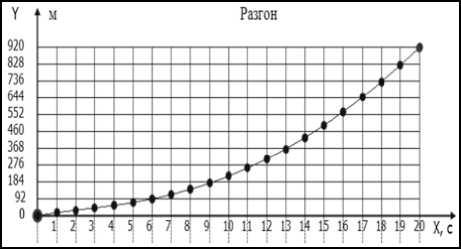
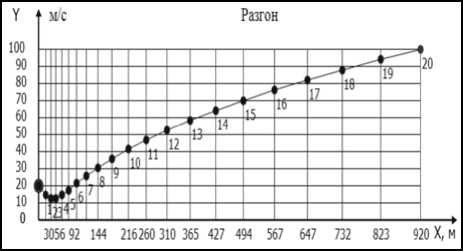
Координаты ^[ S ]                             Фазовые координаты [ V , S ]

Синтез финитного закона управления на основе заданного постоянного программного ускорения Synthesis of finite law of control based on a given continuous program acceleration честве иллюстративного примера приводится решение задачи разгона материальной точки из [2, с. 23].

Пример (см. рисунок). Объект разгоняется в течение T = 20 c от начальной скорости V ₀ * = 20 м/с до конечной скорости V k = 100 м/с. При расчете коэффициентов к о и к 1 начальная скорость объекта была задана равной V ₀ = - 20 м/с, а «жесткость управления» принималась равной A T = 3 с.

Закон управления, соответствующий заданным условиям задачи, принимает вид: и = - 0,667 + 2 t - 0,333 V . Следовательно, обратная связь о кинематике движения в алгоритме управления ( и ) осуществляется на основе данных смешанного программного управления, являясь функцией временного ( t ) и координатного программных управлений по скорости ( V ). Координаты объекта (S) вычислялись численным интегрированием системы уравнений

V = и ,

, S' = V .

В компьютерную программу блока интегрирования был включен метод Рунге-Кутты четвертого порядка точности. Шаг интегрирования составлял 1 с.

Заключение . По результатам выполненного исследования можно сделать следующие выводы:

• 1.    Количественное представление о параметрах позиционирования звеньев биомеханической системы на границе фаз упражнения задается численной величиной запланированных значений обобщенных координат модели в узловых точках траектории.

• 2.    Аналитическое представление эволюции управляющих воздействий должно удовлетворять принципу совместности запланированных значений программного и финитного управлений в узловых точках траектории биомеханической системы, кинематическое состояние которых и является целью управления.

• 3.    Фазу разгона в технике спортивных упражнений можно прогнозировать аналитической моделью управления конечным состоянием биомеханических систем на основе синтеза программного и финитного законов движений.