Синтез псевдоградиентных процедур привязки изображений по критерию максимума взаимной информации

При решении практических задач более эффективными и гибкими являются рекуррентные процедуры, работающие в пространственной области. При этом высоким быстродействием обладают процедуры, основанные на псевдоградиентной безыдентификационной адаптации:

аt = аt-1 - лt в(J, аt-1) , где а - вектор оцениваемых параметров; в -псевдоградиент целевой функции J; Л t -матрица усиления; t - номер итерации. Псевдоградиент в находится на t-ой итерации по локальной выборке Zt = {z^ Sj1} отсчётов z(2 с привязываемого и j с опорного изобра-(2) женин, где jt - координаты отсчетов zjt , по-~(1)   ~(1)П- павших в локальную выборку; z-jt = z (jt, at-1) - отсчеты непрерывного изображения z(1), полученного из опорного изображения по оценкам аt । модели привязки с использованием некоторой интерполяции. Объем выборки ц равен числу отсчетов zj'. ПГП работают в условиях априорной неопределенности, применимы к обработке изображений с плавно меняющейся неоднородностью, не требуют предварительной оценки параметров изображений.

Псевдоградиентные процедуры [2] основаны на оптимизации многомерной целевой функции качества оценивания, характеризующей меру подобия (или различия) между парами изображений. Существует множество мер [3], которые могут быть использованы в качестве целевых функций. Среди мер подобия можно выделить корреляционное отношение, энергия совместной плотности распределения вероятностей яркостей, взаимная информация Шеннона, взаимная информация Реньи, взаимная информация Тсаллиса, меры F-информации, стохастическая и детерминированная смена знаков, порядковая мера, коэффициенты межкадровой корреляции, Танимото, минимального отношения, ранговой корреляции Спирмана, ранговой корреляции Кендалла, наибольшего отклонения. К мерам различия изображений, которые могут быть использованы в качестве целевых функций, можно отнести средний модуль разности, медианы модулей разности и квадрата разностей, средний квадрат межкадровой разности, нормированный средний квадрат межкадровой разности, инкрементальное знаковое расстояние, дисперсия отношения яркостей, дисперсия отношения отображения яркостей, среднее ранговое расстояние, энтропия совместной плотности распределения вероятностей яркостей, исключающая F-информация.

Исследования показали, что в условиях сильных яркостных искажений изображений перспективными являются меры, основанные на информационных критериях [4], в частности взаимная информация (ВИ). Применение ВИ в качестве целевой функции при обработке изображений долгое время сдерживалось требованием больших вычислительных затрат, особенно для методов прямого вычисления ВИ. Снизить указанное требование при решении задач оценивания параметров изображений позволило появление методов восстановления плотности распределения вероятностей (ПРВ) яркостей изображений [5] по ограниченной выборке. Это дало возможность синтеза реализуемых процедур. Тем не менее, их реализация в современных информационных системах, характеризующихся все более высокими скоростями передачи данных, остается проблемной, так как требуемый объем вычислений остается большим, а вопросы синтеза и анализа рекуррентных процедур по критерию максимума ВИ изображений – исследованными слабо.

Эффективность взаимной информации как целевой функции. Исследована эффективность использования ВИ в качестве целевой функцией в ПГП при различных видах яркостных искажений: аддитивные несмещенные гауссовы шумы, линейные и нелинейные искажения проведено на имитированных и реальных спутниковых изображениях. Для сравнительного анализа в качестве целевых функций исследованы также средний квадрат межкадровой разности (СКМР) и коэффициент межкадровой корреляции (КМК) [6, 7]. Целевые функции, выбранные для исследования, имеют разную размерность, поэтому их численные значения нормировались. Для наглядности в качестве исследуемого параметра использован взаимный сдвиг h изображений вдоль одной из координатных осей. Заметим, что выбор в качестве α только сдвига, незначительно ограничивает общность рассмотрения, поскольку для каждой точки пространства оцениваемых параметров проведенные исследования справедливы и для евклидова расстояние рассогласования (ЕРР) оценок, комплексно характеризующего произвольный набор параметров модели привязки.

На рис. 1 приведены графики зависимости целевых функций от сдвига h при шумах, дисперсии которых различаются в 10 и 100 раз, где q =дисперсия шума/дисперсия сигнала. Кривая 1 соответствует СКМР, кривая 2 – КМК, кривая 3 – ВИ (та же нумерация кривых на рис. 2 и 3. Видно, что при небольших шумах наибольшую крутизну имеет ВИ, что при использовании этой целевой функции в рекуррентных процедурах обеспечит и большую потенциальную скорость сходимости оценок параметров. Эта же функция благодаря «острому» экстремуму обеспечит и большую точность оценок. Однако при увеличении интенсивности шума крутизна и максимум характеристики ВИ падают. При изменении q от 0 до 2 величина максимума уменьшается в 15 раз.

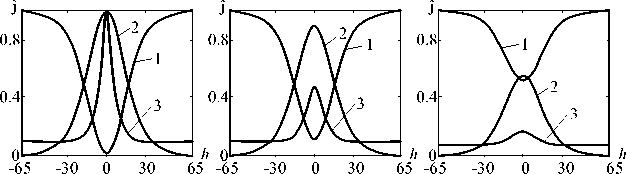
Рис. 1. Целевые функции при разном отношении шум/сигнал

В рекуррентных процедурах оценивания потенциальную скорость сходимости оценок параметров во многом определяет максимальная крутизна K целевой функции. Зависимости максимальной крутизны СКМР, КМК и ВИ от q приведены на рис. 2. При небольших шумах кривая ВИ имеет существенно большую крутизну по сравнению с СКМР и КМК, однако по мере увеличения шума по этому показателю она начинает им проигрывать. Если изображения отличаются только аддитивными шумами, использование в качестве целевой функции ВИ при q >0,1 уже потенциально не обеспечит большую скорость сходимости оценок привязки по сравнению с использованием СКМР и КМК.

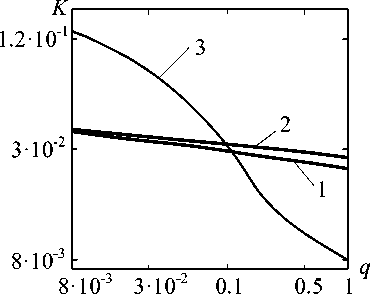
Рис. 2 . Зависимость максимальной крутизны от отношения шум/сигнал

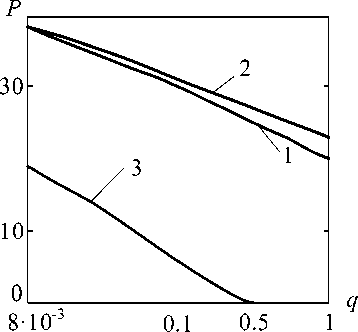
Рис. 3 . Зависимость эффективного рабочего диапазона от отношения шум/сигнал

Еще одним важным на практике показателем является эффективный рабочий диапазон P ПГП, под которым в этой работе понимается подобласть области определения параметров привязки, в которой достигаются требуемые точностные показатели при заданных ограничениях (вычислительные затраты, число итераций и др.). Условием вхождения точки пространства оцениваемых параметров в эффективный рабочий диапазон может являться крутизна целевой функции в этой точке, превышающая некоторое критическое значение. Для примера на рис. 3 приведены зависимости потенциального рабочего диапазона от q при критическом значении крутизны 0,035. Видно, что по этому показателю ВИ примерно вдвое уступает СКМР и КМК, которые при отсутствии шума обеспечивают практически одинаковый P. С ростом q до 1 рабочий диапазон уменьшается для КМК в 1,65 раза, для СКМР - в 1,9 раза, а для ВИ с заданной эффективностью оценивание возможно лишь до q~0,5.

Исследование целевых функций на изображениях с линейными яркостными искажениями показало, что лучшие результаты обеспечивает ВИ, немного отстает КМК. Однако учитывая значительный выигрыш КМК по вычислительным затратам относительно ВИ, в большинстве случаев предпочтителен первый. Но для изображений, имеющих значительные нелинейные яркостные искажения, единственной мерой, обеспечивающей приемлемую эффективность, оказалась ВИ.

Оценка градиента взаимной информации изображений. Ключевым этапом при нахождении псевдоградиента ВИ является оценка ПРВ яркостей изображений по локальной выборке. Воспользуемся методом окна Парзена [8], при котором оценка ПРВ находится как суперпозиция аппроксимирующих функций, центрированных на яркостях отсчетов, попавших в локальную выборку. Тогда вероятность яркости z:

- p(z) ~ л 1Ё R (z - zi)

i = 1

где R ( • ) - аппроксимирующая функция.

Для нахождения энтропии изображения по восстановленной ПРВ яркостей обычно используют дополнительную выборку Z b объема ^ b . При этом энтропия рассчитывается как выборочное среднее логарифма p ( Z b , Z a ):

HI ^{( Z )} = ^- Л ^- Ё   log ( p ⁽ z i , Z a ))

^zi ^E Z b

Тогда для псевдоградиента ВИ получаем:

в = — Ё z(W(1) - Wz(1’2))x

О Lib i e Z b j e Z a

x(zi"

-

j)

d ( ~P

-

d α

где:

wz^ =

W <*’2)

z

j)

R (zt(1) - ~7(1))

Ё R(zi" - j)

^z j ^e Za                    .

;

R (~<'> - j) R (z(2) - z < 2>)

= ЁR(z«- -?j") R(z»' -zj2>)'

z j E Z a

о - параметр ширины аппроксимирующей функции.

В релейном варианте синтезированная ПГП принимает вид:

^a t + 1 = ^a t - ^л t sign ^e

,

где: β - определяется выражением (1).

Отметим, что при нахождении псевдоградиента ВИ наиболее затратной с вычислительной точки зрения является оценка энтропии (совместной энтропии) исследуемых изображений, которая производится на каждой итерации оценивания. Поэтому сокращение вычислительных затрат при оценке энтропии дает существенное увеличение быстродействия ПГП. Для решения поставленной задачи воспользуемся процедурой скользящего контроля [9], используемой в задачах машинного обучения при оценке вероятностей по методу окна Парзена. В соответствии с этой процедурой из исходной локальной выборки объемом µ формируется µ возможных разбиений. Каждое разбиение делится на две части, одна из которых состоит из единственного отсчета, используемого для оценки энтропии, а вторая ‒ из всех оставшихся отсчетов, которые используются для оценки ПРВ яркостей изображения. Выигрыш в вычислительных затратах при этом достигается за счет того, что на каждой итерации используется одна и та же выборка, как для оценки распределения, так и для оценки энтропии изображений:

Hi(Z) = -^1 S logp 1 S  R(z, zi ■ Zt     V     zje Ztj *1

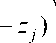
где z i , ^z j ^e Z t . Применяя к решаемой задаче данный подход, для псевдоградиента ВИ получаем выражение:

в = ¹ S I W ^1) - W ^^1,2) V ( ~ ⁽¹⁾ - ~ /⁽¹⁾ ) х zz

v    dx    da      dy    da j подстановка которого в (2) дает еще один вариант релейной ПГП по критерию ВИ.

Экспериментальные исследования, проведенные на имитированных изображениях при использовании в качестве модели привязки модели подобия, показали, что по сравнению с алгоритмом EMMA [10] вычислительные затраты на нахождение энтропии изображений сокращаются примерно на 10-15%, а дисперсия погрешности при этом увеличивается в среднем лишь на 2,5%.

Вычислительная сложность синтезированных процедур. Детальный анализ вычислительных затрат на нахождение псевдоградиента ВИ требует учета не только особенностей и структуры расчетного соотношения, но и большого числа других влияющих факторов (скорость и условия считывания отсчетов изображений, тип вычислительного устройства, время на операции обращения к памяти, пересылки и др.). Многие из этих факторов зависят от конкретных устройств регистрации изображений и вычислительных средств. Ниже приведены некоторые результаты анализа вычислительной сложности только расчетных соотношений, реализующих предложенные способы, через число операций (сложения (+), вычитания (-), умножения ( ^x ), деления ( •• ), взятия корня (^), тригонометрических функций ( sin, cos ), интерполяции яркости одного отсчета ( ^z ), экспоненцирования ( exp ).

Получены расчетные выражения, позволяющие найти вычислительные затраты и быстродействие разработанных способов нахождения псевдоградиента ВИ для конкретных вычислительных средств. Так, суммарные вычислительные затраты для вычисления псевдоградиента:

N = c₊N₊ + c_xN_x + c.N. + c ~ N ~ + ±   ±      x x       .    .       z z

+ c Nii I+ c sin Nin + CexnNexn sui sui     exp exp

, где             c ± , c x , ^c ^ , ^c ~ , c p, ^c sin , ^c _e x             и

N ± , N _x , N ^ , N ~ , Np , N _sin, Nx - время и число выполнения соответствующих операций.

Проведено также сравнение вычислительной трудоемкости с ситуациями использования в качестве целевой функции СКМР и КМК. Так в таблице приведено число операций, требуемое для нахождения псевдоградиента СКМР, КМК и ВИ как функции μ при аффинной модели деформаций и билинейной интерполяции яркостей.

На рис. 4 для примера приведены графики зависимости времени вычисления псевдоградиента ВИ для процессора AMD Turion II X2 M500, при этом кривая 1 соответствует алгоритму EMMA, а кривая 2 – алгоритму вычисления по методу скользящего контроля. Последний обеспечивает меньшие затраты, при этом выигрыш в быстродействии растет с ростом μ. Однако при обоих способах зависимость вычислительных затрат от объема выборки носит квадратичный характер, тогда как аналогичные зависимости для СКМР и КМК линейные.

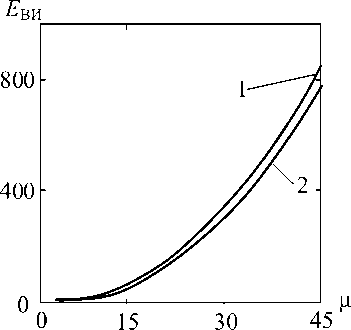
Рис. 4. Зависимость времени вычисления псевдоградиента от μ

Таблица. Число операций на нахождение псевдоградиента для одной итерации

Операция	Число операций
	СКМР	КМК	ВИ (EMMA)	ВИ (скользящий контроль)
+, ‒	34 ц- 2	38 ц- 5	16 ц 2 + 8 ц	1б ц 2 + 8 ц
X	14 ц + 10	18 ц + 11	( 34 ц 2 + б)/ 2 + 10	( 34 ц 2 - 28 ц )/2 + 10
+	10	20	4 ц 2	4 ц 2 - 4 ц
z	4 ц	4 ц	8 ц	8 ц
sin, cos	2	2	2	2
	-	5	1	1
exp	-	-	ц 2	ц 2 -ц

Выводы:

• 1.    Исследование эффективности использования в задаче привязки изображений в качестве целевой функции ВИ при различных видах яркостных искажений (аддитивный несмещенный шум, линейные и нелинейные искажения) показало, что при рекуррентном оценивании для изображений, не имеющих мультипликативных яркостных искажений, в качестве целевой функции целесообразно использование СКМР. При небольших аддитивных шумах наибольшую крутизну имеет ВИ, что потенциально обеспечивает и большую скорость сходимости оценок параметров привязки. Однако при увеличении шума крутизна и максимум характеристики ВИ резко уменьшаются. Для изображений, яркости которых связаны линейным преобразованием, лучшие результаты показывает ВИ, немного отстает КМК, для изображений, имеющих значительные нелинейные яркостные искажения, единственной мерой, обеспечивающей приемлемую эффективность, является ВИ.

• 2.    При синтезе ПГП использован метод окна Парзена, при котором оценка распределения вероятностей находится как суперпозиция одинаковых по форме аппроксимирующих функций,

• 3.    Проведенный анализ вычислительных затрат на расчет псевдоградиента целевой функции показал, что способ вычисления, основанный на методе скользящего контроля, обеспечивает выигрыш в быстродействии, который растет с увеличением объема выборки. Так, при μ=10 он составляет 9 %, при μ =30 – 10%, μ =50 – 16%. Отметим также, что при μ =10 вычисление псевдоградиента ВИ с использованием метода скользящего контроля по сравнению с СКМР требует вычислительных затрат в 10,7 раз больше, а с применением алгоритма EMMA – в 12,4 раз больше. При μ=30 – уже соответственно в 34.5 и 37.8 раз больше.

центрированных на яркостях всех отсчетов выборки. Показано, что по сравнению с «гистограммными» методами он дает существенно лучшее качество оценивания ПРВ. При нахождении псевдоградиента ВИ наиболее затратной с вычислительной точки зрения является оценка энтропии исследуемых изображений. Предложенный способ оценки энтропии, основанный на процедуре скользящего контроля, дает по сравнению с алгоритмом EMMA сокращение объема выборки до двух раз. При этом вычислительные затраты на нахождение энтропии изображений сокращаются на 10-12 % при незначительном увеличении дисперсии погрешности (единицы процентов).

Исследование выполнено при финансовой поддержке гранта РФФИ № 13-01-00555 а b государственного задания Минобрнауки России № 2014/232.