Синтез системы автоматического управления глубиной резания круглошлифовального станка

Введение. Качество продукции машиностроительного производства во многом определяется эксплуатационными свойствами входящих в ее состав деталей, а это в свою очередь, ведет к росту требований к изготавливаемой продукции по критериям точности, шероховатости поверхности, гарантировании ее физико-механических свойств и т. д. Одно из важнейших мест в ряду технологических процессов занимают технологические процессы финишной обработки, наиболее распространённым из которых является процесс шлифования [1–6]. Специфика развития машиностроительного производства, заключающаяся в широком внедрении в промышленную практику шлифовальных станков с ЧПУ, требует осуществлять автоматическое управление процессом обработки, т. е. необходима разработка систем автоматического регулирования параметров процесса шлифования в соответствии с выбранными критериями качества обработки. Решение данной задачи осложняется такими особенностями процесса шлифования, как нестационар-ность, недетерминированность и нелинейность [7–12], для учета которых необходимо выполнять постоянную оценку состояния технологической системы с учётом динамики процесса. Такую возможность дает применение системы автоматического управления процессом обработки. Из-за необходимости учета и описания ряда факторов, наиболее существенными среди которых является учет динамики процесса шлифования, синтез системы автоматического управления (САУ) процессом шлифования представляет собой достаточно сложную задачу [13–17].

Достаточно часто для уточнения характеристик модели управления процессом используют синтез системы обработки наблюдений, введение в контур управления адаптации по формальным [16, 18, 19] либо физическим параметрам [20–22]. При описании системы управления процесс круглого шлифования может быть представлен звеном задержки [17, 20, 22] либо его

Технология упрощенной моделью – апериодическим звеном первого порядка [16, 21], что является грубым приближением.

Целью статьи является поиск по известным параметрам звеньев технологической системы параметров коррекции, обеспечивающих устойчивость системы автоматического управления глубиной резания на операции круглого шлифования, при условии отсутствия колебательности процесса в случае изменения режимов обработки.

Материалы и методы. Рассмотрим систему управления подачей шлифовального станка (рис. 1), включающую в себя двигатель постоянного тока 1 (например серии 4ПБ), кинематически связанный со шлифовальной бабкой станка 4 через редуктор 2, и ходовой винт 3. Контроль снимаемого припуска производится устройством активного контроля 5, связанного с дифференциальным усилителем 6, на второй вход которого поступает сигнал, соответствующий размеру заготовки D ₀. Питание двигателя 1 осуществляется через усилитель-преобразователь 7. Обрабатываемая деталь 8 установлена в центрах 9 и приводится во вращение приводом 10.

От системы управления врезной подачей 11 через цифро-аналоговый преобразователь 12 напряжение U _вх, которое представляет в определенном масштабе значение нужной величины снятия припуска, поступает на сравнивающее устройство 13. На второй вход сравнивающего устройства 13 с дифференциального усилителя 6 поступает сигнал U пр , значение которого пропорционально величине снятого припуска, информация о величине которого поступает на вход дифференциального усилителя 6 от прибора активного контроля 5. После сравнения сигналов U_вх и U пр формируется сигнал ошибки ∆ U, поступающий после обработки в усилителе-преобразователе 7 как напряжение U на двигатель 1, и, как результат, шлифовальная бабка 5 перемещается на величину, необходимую для обеспечения заданной глубины резания.

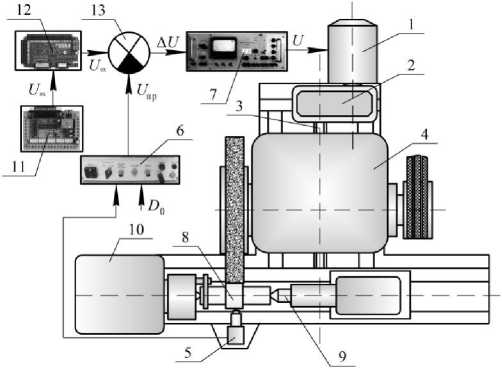
Рис. 1. САУ врезной подачей круглошлифовального станка

Для анализа САУ необходимо иметь ее математическое описание. Для системы управления, показанной на рис. 1, оно может быть представлено описанием ее звеньев в операторной форме

[16–23]: W 1 (p)	k 1        .	к 1 = 10...100;   T 1   <   0 , 1 c ;
	T 1 p + 1 ’
W 2 ( p )	к 2	к 2 = 1 . 3 , 5 ; Te <  0 , 1 c ; Tm = 0 , 1 . 0 , 7 c ;
	TeTmp 2 + Tmp + Г
W ( p )	= кз;  к 3 = 0 , 01. . 0 , 1 ;
W 4 (p)	= к 4 ;	к 4 = ( 4 ... 8 ) / 2 я мм/об ;
W 5 ( p )	exp( - r p ) = к 5                 ’ p	T- время одного оборота детали с ; к 5 <  1 ;
W 6 =	к 6 ;	к 6 = 0 , 01 . 0 , 12 ;
W 7 =	к 7      .	к 7   <  0 , 15 ; T 7   <  0 , 05 c .
	T 7 p + 1 ’

Богуцкий В.Б., Шрон Л.Б.

Синтез системы автоматического управления глубиной

резания круглошлифовального станка

Для моделирования поведения системы при произвольном входном воздействии необходимо упростить выражение звена задержки exp — т p), входящего в состав передаточной функции W₅ ( p ) , описывающей технологический процесс удаления припуска. Среди возможных выберем наиболее общий подход, позволяющий уточнять модель по мере необходимости.

Представим звено задержки exp( — т p ) приближенным выражением

n

—

„^{— т} p ~

e    ~

та p n

1 + ip

—

n, а 1

к          n )

где а может выбираться в пределах 0 <  а < 1 . Положив а = 0 , получим

e ^{— т p}

.

n

f1 + т Р) k      n)

Применив разложение по формуле бинома, перейдем к тождественной форме

e—т p =           ,

Ё a i p

i = 0

где a, = C i ( т/ n ) , C ni - биномиальный коэффициент.

Реакцию звена, представленного в той или иной форме, можно получить на основе обратного преобразования Лапласа:

y(t) "  invlaplace (X • W/p,p,t);

K(t) := invlaplace (X ■ exp^ T - p^lp,p,f);

Рис. 2. MAPLE-интерпретации для единичного входного воздействия X

На рис. 2 _{w =} ^fm + — ) — результат аппроксимации звена задержки exp — p ) звеном n -го к      n )

порядка.

На рис. 3 показаны графики переходного процесса при единичном входном воздействии X = 1( t ), T = т = 0,1 с и разных значениях n , из которого видно, что, выбирая n , можно уточнять результат моделирования звена задержки, что решает одну из поставленных задач.

Таким образом, технологический процесс шлифования может быть описан линейным выра-

жением, учитывающим процесс задержки врезной подачи w ( p ) = | 1 + Tp k      n

—

n и процесс удале-

ния припуска Wpr(p) = —, имеющий интегральный характер. С учетом выполненных преобра-p зований окончательно запишем для технологической операции шлифования

— n k 5 f 1 + Tp)

w(p) = W(p)w„(p> = —i----n-L- p

.

Технология

Одной из основных является задача обеспечения устойчивости при заданном качестве переходного процесса. На устойчивость и качество работы САУ оказывают влияние изменения графика технологического процесса для деталей различного типа, настройки ЧПУ, параметров инструмента, заготовки, материала и другие факторы, вызывающие отклонение режима ее работы. Отдельный учет указанных факторов является трудоемкой задачей [17, 20, 21].

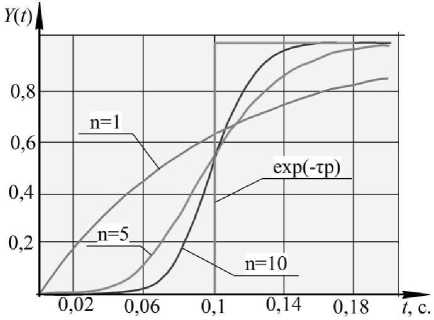
Рис. 3. Графики переходного процесса при единичном входном воздействии (приближение звена задержки)

Воспользуемся комплексным подходом, основанном на методе замещения коэффициентов операторной дробно-рациональной передаточной функции при выборе собственного оператора желаемой передаточной функции [18, 24]. Для этого введем последовательную коррекцию передаточной функции САУ (рис. 4), положив W 0( p ) = 1 W C ( p ) , где W ( p ) - числитель нормализованной передаточной функции САУ W ( p ) , изображенной на рис. 1

W ( p ) W 2 ( p ) W 3 ( p ) W ( p ) W 5 ( p )

W ( p ) =

.

⁺    ( p )   2 ⁽ p )   3 ⁽ p )   4 ⁽ p )   5 ⁽ p )   6 ⁽ p )   7 ⁽ p )

В рассматриваемом случае после преобразований найдем

Wc (p) = k^k^k, (1 + Tp).

Выполнив коррекцию, запишем передаточную функцию САУ в дробно-рациональной форме

W k p =

W ( p )  _    1

W c ( p ) = W z ( p )

где W z ( p ) = Z a_zp ^j .

.j = 0

Введем требование абсолютной устойчивости при апериодическом переходном процессе [23]:

WZ(p) - WQ(p) = (1 + т p)n.

Приняв w ( p ) = '^qp j , запишем .j = 0

nn

Z a j p^J - У. q j p^J = ^{( 1 + т} p ) n .

j = 0              j = 0

Учтя, что ( 1 _{+ т} p ) ⁿ = Zlcip j , где ^cj = т ^j C ^j _n , получим условие реализации наложенного

.j = 0

требования в виде Qj = a₂ - c₂ , которое можно выполнить введением обратной связи (см. рис. 4).

Для формирования обратной связи U _k применим разностную рекуррентную схему [23, 24]. С введением обратной связи эквивалентная передаточная функция САУ приводится к виду

W E ⁽ p ) =        ¹     * ,

^{( 1 +} т p ) где можно принять т = т а"^ .

Богуцкий В.Б., Шрон Л.Б.

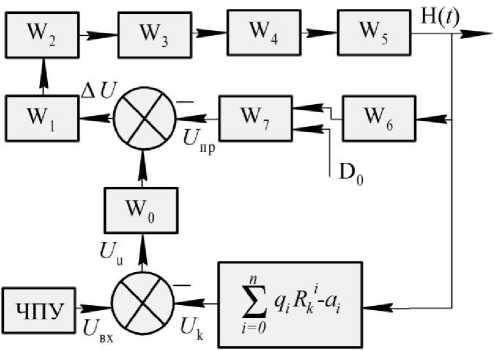
Рис. 4. Функциональная схема САУ

С помощью полученной передаточной функции легко вычисляется реакция на стандартные воздействия, которые могут быть описаны в изображениях по Лапласу.

	H 1 ,                    if  0 <  t <  T i ; H? — H z -------^ ( t - T i ),   ff  T i   <  t <  T 2 ;
X ( t ) =	T 2  - T i H 2 ,                   ff  T 2 <  t <  T 3 0,                         otherwfse

with ymttransy

Tu - ^nj^//»); TO := 20. ■ Tu; X" L;

WEQp) : = 1/sum ^binomial (n, z) • ТиЧ • р^Т/Т^О.-п);

Digits := 20.;

Рис. 5. Алгоритмическая MAPLE-модель САУ

На рис. 6 а приведен график изменения входного воздействия X(t) и выходного сигнала Y ( t ), вычисленного при аппроксимации процесса шлифования апериодическими звеньями первого ( n = 1) и третьего ( n = 3) порядков (реакция системы) в соответствии с MAPLE-описаниями, приведенными на рис. 6 б (Shlif_12.mws).

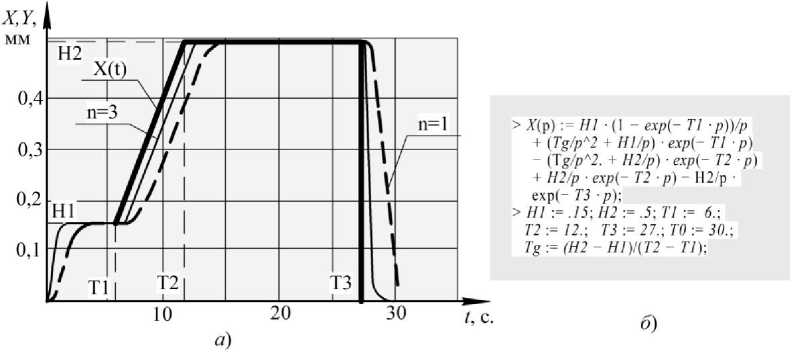
Рис. 6. График изменения входного воздействия X( t ) и выходного сигнала Y( t ), (реакция системы)

Технология

Для упрощения описания входного воздействия при необходимости вычисления реакции на сигнал произвольной формы (например, шумового воздействия) необходимо применение численных методов. В этом случае отпадает необходимость перехода к изображениям, что упрощает алгоритм решения задачи. Задача решается во временной области. Для передаточной функции рассматриваемого типа

W k ( P ) = -v²— ’

Ё ajPJ j=о где по определению W (p) = Y(p) / X(p), Y(p) и X(p) - изображения выходного и входного сигналов соответственно, получим [4] решение относительно изображения выхода:

Y(p) = — (Yn-1)(p) - «n-1Y(p)), anp где Y(n-1)(p) - изображение производной (n - 1)-го порядка.

Изображение производной ( n - 1)-го порядка находится по рекуррентной зависимости:

Y(J)(p) = — ( Y(j-1)(p) - aj-YCp)), где 1 < j < n ; Y04p) = X(p).

Результаты и обсуждение. Полученное решение во временной области приводится к рекуррентному виду

Yj(k) = Yj(k - 1) + ( Yj-1(k) - aj-1Yn(k - 1)) h ; 1 < j < n,

Y n ( k ) = Y n ( k - 1 ) + ( Y n ^{- 1} ( k ) - a_n - 1 Y n ( k - 1 ) ) hja_n , где k - номер шага, h - его величина.

Таким образом, по передаточной функции системы можно сразу получить решение во временной области для входного сигнала и вх произвольной формы, заданного в любом виде (аналитически или таблично). Алгоритмическое MAPLE-решение (Shlif_14. mws) показано на рис. 7 ( U u : = U bx - U k :).

> F[(U] := Uw.

for i to n - 1. do

' nu] := Y[i,k - 7.] + (Y[z - l.,k\ -

Рис. 7. Алгоритмическое MAPLE-решение во временной области для входного сигнала U вх произвольной формы

Заключение. Предложена компоновка системы автоматического управления процессом обработки и разработана математическая модель, представленная описанием ее звеньев в операторной форме, которая учитывает динамику процесса шлифования.

Рассмотренный подход может быть использован при анализе процессов управления объектами, имеющими запаздывание, позволяя получить решение непосредственно во временной области.