Синтез законов управления движением объектов по предписанным траекториям

В различных практических областях ставятся задачи по обеспечению движения объекта по предписанным траекториям. Это задачи управления движением рабочего органа манипулятора, лазерным лучом, промышленными роботами, рабочим органом 3D-принтера, квадрокоптерами и. т. д. Проблемы синтеза законов управления предписанным движением, на данное время до конца не решены, это связано с трудностями при рассмотрении многомерных, нелинейных систем, а также с трудностями аналитического описания предписанных траекторий движения. В большинстве случаев на практике, например, при построении систем управления с промышленными роботами или применения 3D-принтеров, предписанную траекторию движения описать аналитически очень сложно. В этом случае используется подход синтеза на основе табличного задания предписанной траектории движения.

Синтез законов управления в случаях задания предписанной траектории движения в аналитической форме. Рассмотрим объект, описываемый математической моделью в виде x = F(x) + G(x)u,                                 (1)

где x = (x 1 , x₂,..., x_n ) ^T — вектор состояния;

u = (u 1 , u₂, ., u_m ) ^T — вектор управления;

F(x) — в общем случая нелинейная вектор-функция;

G (x) — матрица, элементы которой-нелинейные функции от “ x ”.

Данная структура модели включает в себя и случай линейного объекта:

x = Ax + Bu, где А, В – числовые матрицы.

Предписанная траектория движения задаётся в виде системы аналитических выражений:

^r(x, t) = 0,    r = l,s .(2)

Назначая далее требуемый закон отработки ошибки выполнения программы движения в виде

^^^ = Rr(8,x, t),  Rr(0, x, t) = 0,     8r = ^r(x,t) Ф 0,(3)

синтезируется искомый закон управления из условия обеспечения 8_r ^ 0 в виде

U^i^x)^.(4)

где коэффициенты C i , r = 1, s определяется из следующей системы:

^1Ci(GT(z)^, GT(x)^)= Rt — ^^^           l=XS;(5)

Л             МЛ               МЛмс а искомый вектор управления существует при условии rank (g(x) • ^1=1 Ci^) = rank G(x).(6)

Если данное условие не выполняется, то это говорит о невозможности осуществления движения управляемой системы по заданной (предписанной) траектории.

Пример синтеза алгоритмов осуществления предписанной траектории . В качестве примера рассмотрим управляемый объект, который описывается системой уравнений

( x 1 = —x₂ + u 1 ;

* 2 = * з ;

x 3 = u 2 ;

или x = Ax + Ви,

где

/ 0  -1

A = ( 0   0

) ;     B = (1   ⁰⁾

Поставим задачу осуществления движения системы по траектории, описываемой системой уравнений

( ^p1(x1, x2, x3, t) = x1 + x2 +x3 - 1 = 0;

\^2(*l,*2,*3,t) = x1 — 2x2 — 3x3 — 5 = 0.

Для решения задачи синтеза предварительно выясним вопрос линейной независимости векторов Вт • ^\ Для этого определим

„т . W1 _ Г1  0  01, [11 _ Г11.         от .     _ [1  0  0] . [ М _ Г 1 1

В —=[0 0  1] |J|"I1I'      В 17= [0 0  11 [:2]"1-з1

Согласно [1] закону управления (4), имеем выражения искомых законов f U1 = ^ (12^1 + 4г2 + 16*2 - 4хз);

I U2 = ^ (4Г1 - 47-2 - 12%з).

Моделирование замкнутой системы управления с помощью ППП MATLAB.

Уравнение замкнутой системы исходя из (7) и (10) определяется в виде

( ^х1 = \ ^Х 2

(x3 =

-

- • x

= ^x3^;

-

2;

— x3.

16    ³

Моделирование осуществляется на основе системы (11). На рисунке 1 показана модель, выполненная в пакете Simulink. Результаты моделирования показаны на рисунке. 2.

Таким образом, синтезированный закон обеспечивает движение системы по предписанной траектории, заданной в виде системы уравнений (9). Физическая реализация полученных синтезированных функций U 1 , U₂ не вызывает никаких затруднений.

Модельный пример синтеза адаптивного закона управления программным движением. Пусть объект управления описывается системой

Х = ах + ви + Дах,

,  „    f 0   1\        /0\    .     /а11 а12\                       О

где, а=( q) ; в = (J; Да = (а а ) — параметрические возмущения.

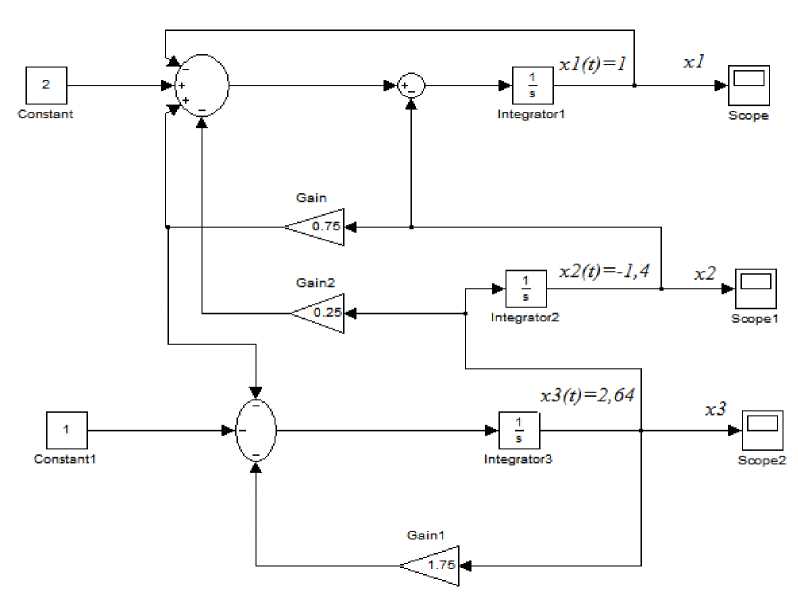
Рис. 1. Моделирование замкнутой системы управления в Simulink.

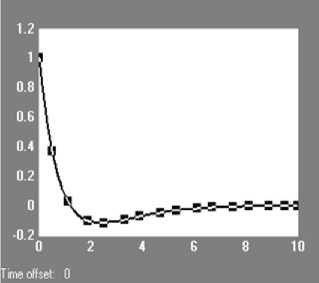
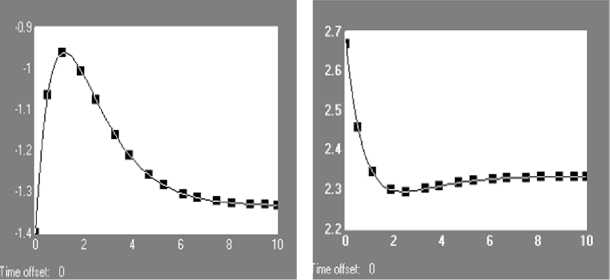
Рис. 2. Результаты моделирования для x 1 (t), x₂(t) x₃(t).

Предписанная программа движения описывается гармоническим законом

X(t) =А sin tot   или

² ^(X 1 ,X 2 ) = X 2 + — - А 2 =0.

U_np строится в виде:

Unp = (а(х) • ^(х, t) - 2x1X2)^-.

Окончательно уравнение замкнутой системы управления с учётом регулятора вида

U= Unp-Cx, структуры

где С - матрица параметрических возмущений, представится в виде:

(

* 2

к

* 1 = * 2 + ^а11 * 1 + ^а12 * 2 ;

а 21 * 1 + а22 * 2 - " 2 [* 1 + а0 (* 1 +		4- л2 «2	) * 2]   C1 * 1   C2 * 2 ;
А _ 2X1X2 C1 =      2 1       «2	( * 2+ i	- Л2);
с - 2х ! С2 =   « 2	(* 2 + 5‘	- Л2).

Проинтегрировав приведенные выражения, можно исследовать процессы

* 1 (t), *₂(t), C 1 (t), C₂(t) и наблюдать фазовые портреты с помощью пакета MATLAB.

Моделирование синтезированной адаптивной системы управления на MATLAB Simulink. Зависимости * 1 (t), *₂(t), C 1 (t), C₂(t) можно исследовать, интегрируя выражения (17) с помощью пакета Simulink (рисунок 3). Полученные результаты моделирования показаны на рисунках 4 – 7, соотношение между изменением выхода параметры и скоростью изменения *₂(t) иллюстрируется фазовым портретом, представленном на рисунке 8.

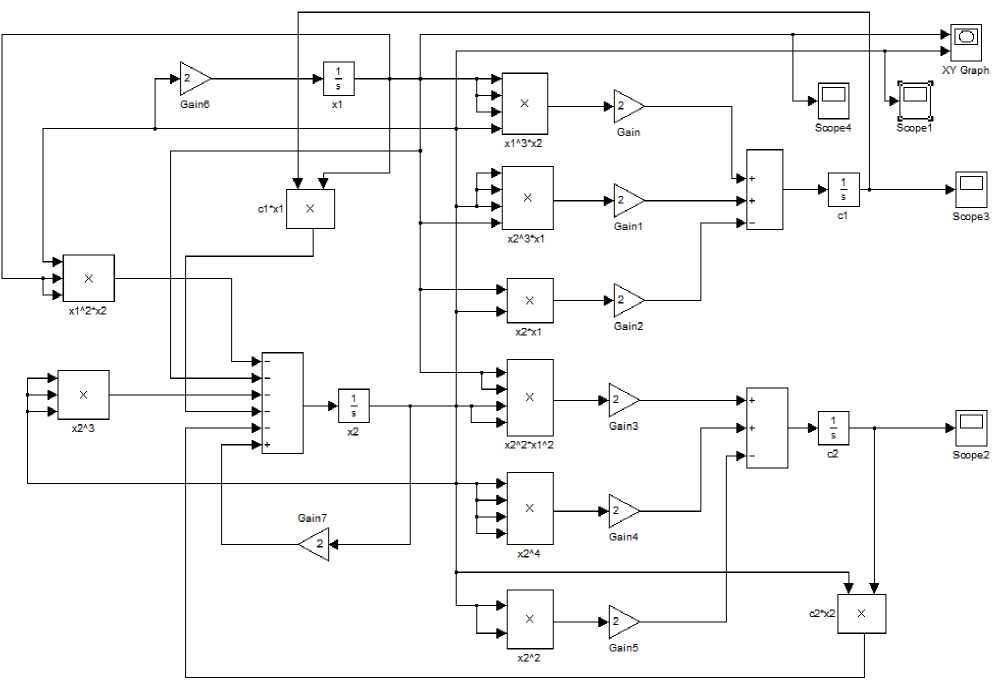
Рис. 3. Структурная схема моделирования синтезированной системы в пакете MATLAB Simulink.

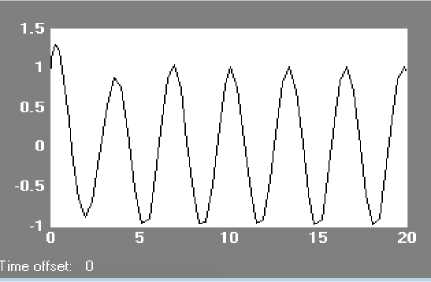
Рис. 4. Процесс на выходе x 1 (t).

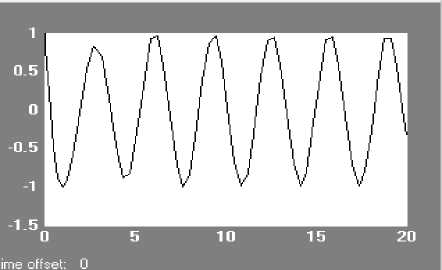
Рис. 5. Процесс на выходе x2(t).

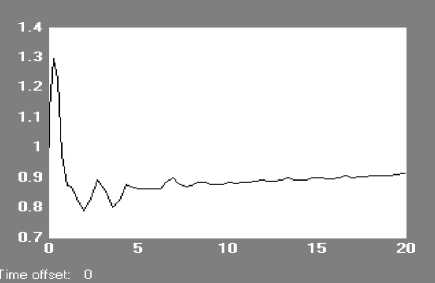
Рис. 6. Процесс на выходе C 1 (t).

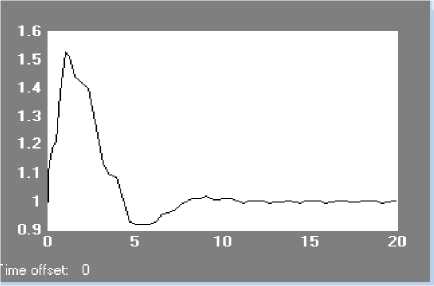
Рис. 7. Процесс на выходе C 2 (t).

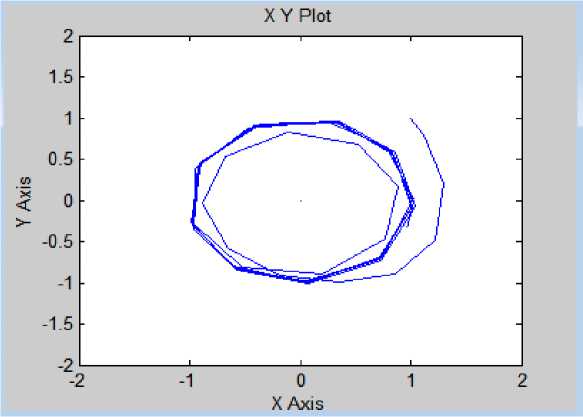
Рис. 8. Фазовый портрет выходных сигналов x 1 (t) и x₂(t).

Данный фазовый портрет полностью подтверждает теоретические выводы и показывает процедуру синтеза (определения) искомых законов управления, когда предписанная траектория задается в аналитической форме.

Подход к синтезу законов управления в случаях задания предписанной траектории движения в табличной форме. Во многих практических важных случаях, например, в задачах робототехники, при автоматизации раскроя и конструирования одежды, использования лазерных технологий микроэлектроники, в системах 3D-технологий и др. аналитическое представление предписанной программы движения вызывает большие затруднения. В этих случаях предлагается следующий подход к синтезу. Пусть объект описывается системой x = f(x,u, t),                                           (16)

где x = (x 1 ,x₂,... ,x_n)^T — вектор состояния;

u = (u 1 , u₂,..., u_m ) ^T — вектор управления.

Требуется синтезировать закон управления по осуществлению траектории движения управляемой системы, заданной в табличной форме (см. таблицу 1).

Таблица 1

Предписанная траектория движения, заданная в табличной форме

tk	t0	t1	t2	t3	...
X 1	x10	x ii	x12	x13	...
x2	x20	x21	x22	x23	...
...	...	...	...	...	...
xn	xn0	x n1	xn2	xn2	...

Для удобства принимается  tk = k,   k = 0, 1, 2..., т. е. вводятся абстрактные дискретные моменты времени.

Математическая модель объекта записывается в дискретной форме

x(k + 1) — x(k)                          x(k + 1) — x(k)

= f(x(k), u(k), k) или -------------- = f(x(k), u(k), k).

t k+1   t k                                         A

Ее представляем в виде

x(k + 1) = x(k) + f(x(k),u(k),k)A,                         (17)

где: x(k) - текущее состояние, x(k +1) - состояние на следующем шаге.

Из выражения (17) можно определить u(k): u(k) = U(x(k),x(k + 1), k, △ ).

Управление будет определяться из условия минимизации квадрата невязки:

^ ^хтабл^(к + 1)   ^xтекущ < ^k+ 1)11 2 ^ min.

Для линейного объекта x = Ax + Bu вышеописанного процедура синтеза приводит к результату

u(k) = -47(ВтВ)-1[2Вт8хтабл(к+1) - 2BT(A5 + E)Sx(k)] =