Система инвариантных признаков для распознавания дактилограмм

Персональная идентификация с помощью распознавания дактилограмм вызывает устойчивый интерес и важна для задач обеспечения безопасности. В настоящее время большинство систем для распознавания дактилограмм использует или анализ структуры полос дактилограммы (папиллярного узора) с помощью оптической нейронной сети, предназначенной для выделения участков прямых линий на изображении [1], или подсчитывает число Галтона (число разветвлений и концов полос дактилограммы) [2]. Все эти методы являются операция -ми с определенными затратами машинного времени. Причем наибольшее время тратится на процесс сравнения набора признаков дактилограммы с признаками дактилограмм в базе данных. В работах [3,4] исследуется метод распознавания дактилограмм по полю направлений. Т.к. вектор признаков представляет собой совокупность коэффициентов разложения по базису Адамара, процедура сравнения с базой данных была сравнительно быстрая. Но этот метод, как показано в работе [5], пригоден только для баз данных небольшого размера (не более 104 элементов). Основная проблема, препятствующая использованию этого метода с базами данных большего размера, заключается в зависимости поля направлений от ориентации дактилограммы. Для того, чтобы использовать метод поля направлений для распознавания дактилограмм в базах данных большего размера (до 106 элементов), необходимо использовать признаки, инвариантные к ориентации дактилограммы.

В качестве таких признаков в данной работе предлагается использовать коэффициенты разложения по базису Цернике Фурье-спектра комплексного поля направлений.

1. Комплексное поле направлений

Поле направлений изображения - это функция координат точки, равная углу касательной к линии уровня интенсивности изображения. Так, если I ( x,y ) есть интенсивность света в изображении, то поле направлений ф x,y ) определяется соотношением:

.   . dI (x, y)/ dx _               m tg ф(x, y) = - —---——,  0 < ф(x, y) < n. (1)

dI ( x , y ) / dy

Очевидно, что угол ф ( x,y ) задает направление, перпендикулярное вектору градиента

( d I ( x , y ) / d x , d I ( x , y ) / d y ) .

Как видно из формулы (1), функция ф (x,y) не инвариантна к повороту исходного изображения I(x,y).

Исходное поле направлений ф(х,у) записывается в фазовую часть изображения v(x,y)• Получа ется изображение ^ (x, y) = exp (i2ф(x, y)), где коэффициент 2 вводится для того, чтобы диапазон значений фазы составлял от 0 до 2п [6]. Данное изображение будем называть в дальнейшем комплексным полем направлений. Оно также не является инвариантным к повороту. Но данное изображение обладает свойством, благодаря которому мы сможем получить набор инвариантных к повороту признаков. Фурье-спектр комплексного поля направлений поворачивается вместе с полем направлений, не изменяя при этом своей структуры. Для получения вектора признаков вычисляется Фурье-образ комплексного поля направлений. На практике коэффициенты разложения по базису Фурье находятся путем вычисления Фурье-образа (преобразования Фурье) от изображения поля направлений.

Двумерное дискретное преобразование Фурье матрицы отсчетов изображения определяется в виде ряда

1 N - 1 N - 1 / 2 _ i \

з(u,v) = т;££F(k,1)exPI -фг(uk + vl) I, (2) N k=0 1=0 V N J где i = V-1, 3(u, v) - Фурье-образ исходного изображения F(k,1), k, 1 - номера отсчетов (дискретные переменные) в плоскости исходного изображения, u, v - номера отсчетов в плоскости Фурье-образа.

Фурье-образ инвариантен к сдвигу исходного изображения, но не инвариантен к повороту. Для получения вектора признаков, инвариантного и к сдвигу, и к повороту, необходимо разложить Фурье-образ по ортогональному базису Цернике. Полиномы Цернике определяются по формуле

^ nm ⁽ r , Ф^ = A n R m ⁽ r ^)eXP⁽ im ^ ), ⁽³⁾

. n + 1 где An = J---T ’

V ^nr 0

⁽ n ^- m ^)/2

R m ( r ) = £ ( - 1) p ( n - p) !

P = 0

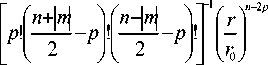
R nm ( r ) - радиальные полиномы Цернике:

R- m (r) = Rm (r), R± (re) -1, n, m - целые числа со следующими ограничениями: n>0, |m|< n ,

(r, ф) - полярные координаты. Вид нескольких полиномов Цернике представлен на рис.1.

Коэффициенты разложения по полиномам Цернике определяются по формуле ^r 0 2 n

C nm = J J E ( r , ф ) ^ nm ( r , ф ) rdrd ф .    (4)

0 0

а)

Рис. 1. Полиномы Цернике: а) 1,1; б) 2,0; в) 2,2

Покажем, что коэффициенты C nm инвариантны к повороту.

Действительно, рассмотрим представление некоторого изображения E ( r, ф ) в виде ряда (4) с коэффициентами (6).

Изображение, повернутое на некоторый угол ф о , выглядит в полярных координатах в виде E ( г, ф + ф о ). Коэффициенты разложения повернутого поля по базису Цернике имеют вид:

r o 2 п

^C nm = J j ^{E (} r , Ф + Ф о ) ^ ‘ nm ⁽ r , Ф ) rdrd Ф = 00

r o 2 п

= A n J J E ( r , ф + Ф _о ) R m ( r ) exp( - im ф ) rdrd ф = 00

= exp(im фо ) An J J E(r, Ф + Фо )Rm (r) x xexp[-im(ф + фо )]rdrd(ф+фо) =

• =    [ 0 = Ф+Ф о ] =

r o 2 п

• =    exp( im ф о ) J J E ( r , 0 ) T nm ( r , 9 ) rdrd 9 =

• =    exp⁽ im ф о ) C nm .

для 57 пальцев (каждый палец вводился 120 раз). Так как при реальном формировании вектора признаков достигнуть полной инвариантности вектора признаков невозможно (всегда есть небольшие отличия) было решено для сравнения разных систем формирования векторов признаков использовать статистические характеристики.

R_ср – среднее расстояние между средними векторами признаков разных отпечатков пальцев, r ср – среднее расстояние между реализациями и средним

rср вектором для всех пальцев, Q = —— - статистиче-Rср

ский показатель раздельности векторов признаков в пространстве признаков. Для идеальной системы признаков Q =0, достигаемая при этом надежность 100%. При Q =1, надежность должна составлять около 50%.

В качестве эталона для сравнения была использована система набора вектора признаков из коэффициентов разложения по базису Адамара [3-5].

Результаты сравнения представлены в таблице 1.

При этом интенсивности коэффициентов исходного и повернутого изображений будут равны:

|C nm | = C nm C nm = ^exp^{( i}m Ф о ^{) C} nm ^exp^{( -} i^m Ф о ) ^C „m =

*

nm nm nm

,

Таблица. 1 Сравнительные характеристики распознавания

Система набора вектора признаков	R ср	r ср	Q
Базис Адамара	4957	1027	0,207
Базис Фурье	1083	186	0,171
Базис Цернике	1041	138	0,132

также, как и их

модули |<€ nm | = C nm | .

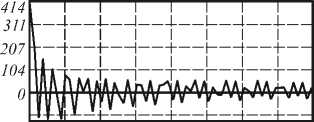
На рис. 2 приведены примеры коэффициентов Фурье и коэффициентов Цернике для исходного и повернутого отпечатков.

Как видно из рис. 2 при повороте исходного изображения вектор признаков не меняется.

2. Результаты эксперимента

Для проверки инвариантности вектора признаков из коэффициентов разложения по полиномам Цернике был проведен вычислительный эксперимент. Для эксперимента была использована база данных, содержащая 6840 различных дактилограмм

Как видно из таблицы, система набора вектора признаков из коэффициентов разложения по базису Цернике по величине Q существенно лучше двух других представленных в таблице систем. Меньшее значение показателя Q означает меньшую вероятность ошибки при распознавании. Наличие некоторого разброса векторов в пространстве признаков можно объяснить наличием (кроме сдвига и поворота) деформации отпечатков.

Заключение

Описанный метод сочетает такие достоинства методов распознавания по коэффициентам ортогональных базисов, как высокая скорость работы и малый размер вектора признаков с достоинствами ме-

тодов распознавания по бифуркациям линий (инвариантность к сдвигу и повороту). Приведенные выше результаты доказывают перспективность использования коэффициентов Цернике в качестве основы для формирования вектора признаков в задачах распознавания дактилограмм. В частности, данный метод позволяет использовать векторы признаков относи- тельно небольшого размера. Использование в качестве компонент векторы признаков коэффициентов ортогональных разложений позволяет упростить саму процедуру распознавания, тем самым ускорив ее, а инвариантность к сдвигу и повороту гарантирует достаточно высокую надежность распознавания в случае практического использования.

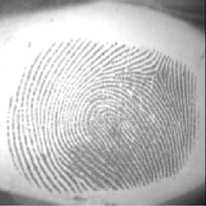
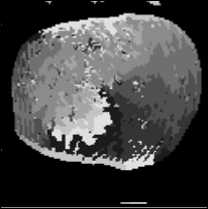
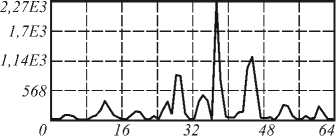
д)   О 16      32       48     64

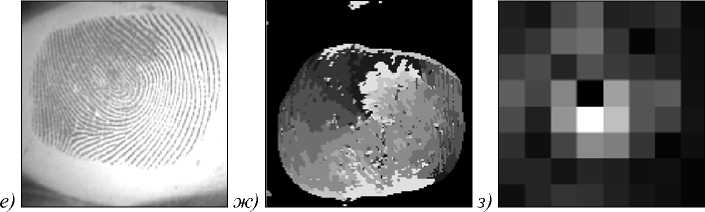
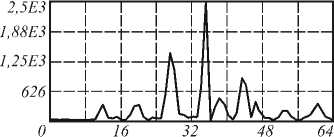
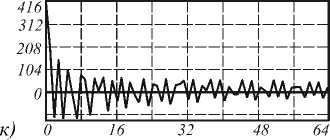
Рис. 2. а) исходный отпечаток пальца, б) его поле направлений, в) центральная часть Фурье-спектра от поля направлений, г) вектор признаков из Фурье-коэффициентов, д) вектор признаков из коэффициентов разложения Фурье-спектра по полиномам Цернике, е) повернутый отпечаток пальца, ж) его поле направлений, з) центральная часть Фурье-спектра от поля направлений, и) вектор признаков из Фурье-коэффициентов, к) вектор признаков из коэффициентов разложения Фурье-спектра по полиномам Цернике

Работа выполнена при поддержке грантов Президента РФ №№ МД-209.2003.01 и НШ-1007.2003.01, а также российско-американской программы «Фундаментальные исследования и высшее образование» («BRHE»).