Система непрерывного тестирования при обучении математическим дисциплинам в вузе

[4, 5]. Выделяются такие преимущества этих подходов, как экономичность (по времени), технологичность, гибкость и возможность индивидуализации процесса обучения.

Анализ литературы, многолетняя педагогическая практика позволяют утверждать, что тестирование при обучении матема- тическим дисциплинам обладает огромными возможностями. Оно может применяться не только для контроля результатов обучения, но и непосредственно для обучения (формирования математических умений), развития мышления, систематизации знаний, воспитания профессиональной направленности. Причем все это мо- жет быть реализовано, в том числе и в форме самостоятельной работы студентов.

Нами предлагается система непрерывного тестирования на примере дисциплины «Линейная алгебра». Эта система представляет собой комплекс тестов различных уровней сложности, охватывающих все темы учебной программы дисциплины, а также необходимые для выполнения тестовых заданий дидактические материалы. Тестирование осуществляется на каждом этапе процесса обучения, начиная с входного контроля (для определения начального уровня подготовки студентов и предварительной их дифференциации) и заканчивая итоговым экзаменационным тестом. Решение тематических тестов осуществляется студентами в форме самостоятельной работы во внеаудиторное время.

При построении системы непрерывного тестирования мы учитывали следующие закономерности процесса обучения, представленные в дидактических принципах: системности и последовательности в обучении, его профилирования, сознательности, активности, самостоятельности и прочности усвоения знаний, индивидуализации и дифференциации обучения.

В соответствии с принципами системности и последовательности в обучении учебные и контрольные тесты системы предлагаются в определенном учебной программой порядке с таким расчетом, чтобы каждый новый элемент содержания учебного материала логически связывался как с предыдущим его элементом, так и с последующим, обеспечивая таким образом наложение новых знаний на усвоенные ранее, что позволит в будущем использовать их как фундаментальную основу для изучения последующего содержания дисциплины. В табл. 1 представлено содержание системы непрерывного тестирования

Таблица 1

Содержание системы непрерывного тестирования по дисциплине «Линейная алгебра»

№ п/п	Раздел дисциплины	Темы учебных тестов
1	АЛГЕБРА МАТРИЦ	1.    Действия над матрицами. 2.    Определители. 3.    Обратная матрица. 4.    Эквивалентные преобразования матриц. Ранг матрицы
2	СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ	1.    Нахождение единственного решения системы уравнений. 2.    Исследование и решение системы линейных уравнений в общем случае. 3.    Модель межотраслевого баланса Леонтьева
3	ВЕКТОРНАЯ АЛГЕБРА	1.    Векторы на плоскости. 2.    Векторы в пространстве. 3.    Линейные векторные пространства
4	ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ	1.    Линейные операторы. 2.    Собственные векторы и значения линейного оператора. 3.    Квадратичные формы
5	ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ	1.    Прямая на плоскости. 2.    Кривые второго порядка. 3.    Прямая в пространстве. 4.    Плоскость

по дисциплине «Линейная алгебра» направлений подготовки бакалавров «Экономика» и «Менеджмент.

Все темы представлены тестами трех уровней сложности. При этом тест каждого уровня предлагается в четырех вариантах и включает 10, 15 или 30 заданий. Задания в вариантах расположены по принципу «параллельности», а также по возрастанию уровня сложности, что способствует более качественному усвоению и закреплению учебного материала. Новым является только используемый подход к построению тестов и выделению уровней сложности. Первый уровень сложности предназначен для отработки базовых математических умений. Задания этого уровня выполняются в одно действие. Второй уровень содержит более сложные задания, для выполнения которых необходимо несколько действий и знание технологии решения стандартных учебных задач. В тесты третьего уровня включаются нестандартные задания, а также прикладные, профессионально ориентированные задачи, предполагающие актуализацию полученных знаний и активизацию мыслительной деятельности студентов при их решении.

В полном соответствии с теорией тестирования используются задания закрытого типа с пятью альтернативными ответами, один из которых является верным. Дистракторы подобраны с учетом типичных ошибок студентов таким образом, чтобы исключить возможность угадывания ответа. Особое внимание уделено заданиям, которые затем используются в следующих разделах дисциплины «Линейная алгебра», а также других математических и экономических дисциплинах.

Приведем примеры тестовых заданий (рис. 1).

Из заданий тематических тестов разных уровней сложности затем составляются итоговые тесты по разделам дисциплины, а также зачетные и экзаменационные тесты.

Согласно принципу профилирования, математическое образование рассматривается с двух сторон. Оно должно быть ориентировано на профиль вуза (факультета), получаемую специальность (направление подготовки),

1

1

2

2

3

1	' 51 '
Для матрицы	02	транспонированной является матрица
- 5    0     a ^	V 1 3 >
V 1 b - 3 a 3 J	, если b равно
102		5334150

Задание относится к разделу дисциплины «Алгебра матриц». Тема учебных тестов «Действия над матрицами». Для его выполнения требуются два действия, продолжительность выполнения – одна минута.

' 4 x 1 - 3 x 2 + 2 x з = 12,

Для системы линейных уравнений ^ 2 x 1 + 2 x ₂ - 3 x 3 = 3, значение x 1

Равно                                [ 5 x ₃ - x 1 - 4 x ₂ = 1

Задание относится к разделу дисциплины «Системы линейных алгебраических уравнений». Тема учебных тестов «Нахождение единственного решения системы уравнений». Для его выполнения требуются три действия, продолжительность выполнения – 2 минуты.

3	Квадратичная форма L = – x 12 – 2 x 22 + mx 32 + 4 x 1 x 2 отрицательно определенной при	– 2 x 1 x 3	+ 2 x 2 x 3 является
1	m = -0,5         2 m e R	3	m >  -0,5
4	m e 0             5 m <  -0,5

Задание относится к разделу дисциплины «Линейные отображения». Тема учебных тестов – к теме «Квадратичные формы». Для выполнения требуются три действия, продолжительность выполнения – две минуты.

Рис. 1. Тестовые задания то есть должно учитывать потребности как общенаучных, так и профильных дисциплин. С другой стороны, математическое образование должно быть направлено на формирование и развитие таких важнейших свойств личности, как ее социальная и психологическая направленность на профессиональную деятельность.

В рамках обучения математическим дисциплинам профилирование реализуется через прикладные профессионально ориентированные задачи, используемые во всех формах учебного процесса как на лекционных, так и на практических занятиях, обязательно включаемых в тематические тесты. Опыт показывает, что для реализации профилирования достаточно включения в тест 10% прикладных задач.

Приведем примеры таких задач разного уровня сложности (рис. 2).

2

4

–1

5

0

Следует отметить, что использование в тематических тестах прикладных, профессионально ориентированных задач означает необходимость пропедевтики специальных знаний, которая может осуществляться в разных формах. Например, решение подобных задач разбирается на лекциях и практических занятиях. Кроме того, в системе непрерывного тестирования предусмотрено использование методических рекомендаций, позволяющих студентам самостоятельно разобраться и выполнить решение задания. Последний подход является наиболее продуктивным, так как дает возможность полноценно описать постановку задания, принятые гипотезы, необходимое моделирование, его решение и анализ.

В соответствии с принципами сознательности, активности, самостоятельности прочность усвоения знаний обеспечивается целенаправленным активным восприятием студентами изучаемых явлений, их осмыслением, творческой переработкой и применением. Базовые математические дисциплины обычно изучаются на младших курсах, но первокурсники не сразу осваивают объективные установки, требования, новые условия образовательного процесса, поэтому для них важно создать условия для преобразования студентов в субъектов этого процесса, осознающих его цели, формы, направленность на самостоятельную работу. В решении этих задач существенно помогает автоматизация системы непрерывного тестирования.

В НИУ «ВШЭ» – Пермь действует индивидуальная автоматизированная система контроля знаний «Траектория», реализующая систему непрерывного тестирования, когда студенты самостоятельно во внеаудиторное время решают учебные тематические тесты по математическим дисциплинам. Тесты компилируются автоматически из имеющейся базы, регулярно обновляющейся и пополняющейся преподавателями кафедры высшей математики. При этом количество решений тестов по одной и той же теме не ограничено. После завершения решения задач студенты сразу же получают результаты с выделенными неверно решенными заданиями.

Получение индивидуальных результатов тестирования с указанием верных и неверных ответов значительно повышает мотивацию обучения студентов, активно стимулирует их к самоанализу собственных результатов, позволяет выявить системные ошибки в изучаемой теме. Поскольку однообразие любой работы снижает интерес к ней, а в математических курсах (и дисциплина «Линейная алгебра» не исключение) встречаются темы, изучение ко-

Предприятие производит два типа продукции, используя три вида ресурсов. На производство одной единицы i-го вида продукции нормы .. f 3 2) - затрат j-го вида ресурса заданы матрицей A = 2 1 .Объемы выпус-. 1 3,

ка каждого из двух типов продукции заданы матрицей B = 1 g^g i - Сто-

имость единиц каждого ресурса задана матрицей P =(21 18 20). Полная стоимость всех затраченных ресурсов составит

1	65700 денежных единиц	2	65740 денежных единиц	3 65670 денежных единиц
4	56760 денежных единиц	5	Правильного ответа нет

Задание относится к разделу дисциплины «Алгебра матриц». Тема учебных тестов «Действия над матрицами». Для выполнения требуются два действия, продолжительность выполнения – одна-две минуты.

₂ Если при цене p = 99 объем спроса составил q = 3, а при цене p = 51 объем спроса составил q = 9, то линейная зависимость между ценой и объемом спроса будет представлена в виде

p + 8 q + 123 = 0

p + 4 q = 87

Задание относится к разделу дисциплины «Элементы аналитической геометрии». Тема учебных тестов «Прямая на плоскости». Для выполнения требуются два действия, продолжительность выполнения – одна минута.

Структурная матрица торговли двух стран имеет вид A =

f 0,3 0,2 ) 1 0,7 0,8 J ^-

Для сбалансированной торговли соотношение национальных

доходов этих стран составляет

1     2:7

4     1:1

2    1:2

Не хватает данных

Задание относится к разделу дисциплины «Линейные отображения». Тема учебных тестов «Собственные векторы и собственные значения линейного оператора». Для выполнения требуются два действия, продолжительность выполнения – одна минута.

Рис. 2. Примеры прикладных профильно ориентированных задач

торых требует решения большого числа однотипных задач, без чего невозможно выработать устойчивые знания и умения. При этом удержать внимание студентов помогают тесты с выборкой ответов. На первый взгляд кажется, что выбрать из предложенных ответов правильный значительно проще, чем решать задания по стандартной схеме, но в реальности оказывается, что, отвечая на вопросы теста, студент проделывает более объемную и кропотливую работу,

2 8 q = 123 – р

3 p = 8 q + 75

5 4q = р – 15

3   3:5

нежели при обычном процессе решения заданий.

Автоматизированная система тестирования помогает также реализовать индивидуализацию обучения, состоящую в организации учебного процесса с учетом индивидуальных особенностей студентов, позволяющую создать оптимальные условия для реализации потенциальных возможностей каждого студента.

Вход в индивидуальную автоматизированную систему кон- троля знаний «Траектория» осуществляется по личному паролю. Студенты имеют возможность самостоятельно, не торопясь, необходимое число раз выполнять решения тематических тестов. При этом они не боятся совершать ошибки. Наоборот, они понимают, что для того чтобы перестать делать ошибки, существует единственный путь: делать ошибки, но затем находить их и исправлять. Иначе говоря, чтобы не делать ошибок, нужно вволю «нао-шибаться». Как правило, обычных «типовых» упражнений на практических занятиях для этого недостаточно.

Ошибка, не замеченная в процессе самостоятельной работы, всплывает на контрольной работе. Студент только тогда перестанет ошибаться, когда ответственность за полученный результат полностью ляжет на него самого, когда он осознает, что только он сам (а не сосед по аудиторному столу и не преподаватель) сможет отыскать выход из создавшейся ситуации, что только от качества его собственной самостоятельной работы зависит конечный результат. Регулярное решение тематических тестов позволяет студентам отработать устойчивые умения и знания согласно их желаниям и возможностям, помогает подготовить их к выполнению итоговых работ.

С точки зрения индивидуализации обучения важно, что тесты имеют разноуровневый характер, так как список заданий итоговых тестов по разделам дисциплины, а также зачетных и экзаменационных тестов делится на обязательную и необязательную части. Обязательная часть соответствует базовому уровню знания. Так, если тест состоит из десяти заданий, то, как правило, включает 7–8 заданий базового уровня, а 2–3 задания рассчитаны на более глубокие знания. Если в тесте 30 заданий, то на обязательную часть отводится примерно 20–22 зада- ния (из них 13 – 15 заданий – типовые «простые»), остальные – задания повышенного уровня. Правильно выполнив задания обязательной части, студент получает «зачет» по теме (разделу) или экзамену (зачету). Необязательная часть рассчитана на более глубокие знания, она готовит студентов к решению сложных задач.

Преподаватель имеет возможность проконтролировать работу студентов посредством индивидуальной автоматизированной системы контроля знаний «Траектория» и увидеть общую картину, например, как усвоена тема в группе, какова подготовленность отдельных студентов, на что следует еще раз обратить внимание при изучении темы.

Наблюдение за работой студентов через индивидуальную автоматизированную систему контроля знаний «Траектория» позволяет также осуществить дифференциацию обучения, означающую такую форму организации учебной деятельности, при которой учитываются склонности, интересы и способности студентов, но при этом не снижается общий (базовый) уровень математической подготовки. Дифференциация предполагает создание на основе определенных признаков (интересов, склонностей, способностей, достигнутых результатов) мобильных или стабильных учебных групп, позволяющих сделать содержание обучения и предъявляемые к студентам требования существенно различными.

Выделение слабо и хорошо успевающих групп студентов помогает в дальнейшем преподавателям при планировании практических занятий. Для хорошо успевающих студентов подготавливаются дополнительные или более сложные задания, им предоставляется возможность работать на занятии самостоятельно или под контролем и с консультациями преподавателя по мере необходи-

25%    ^0%

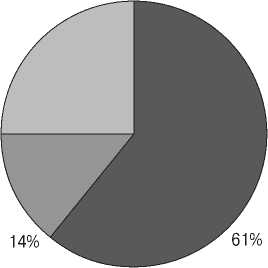
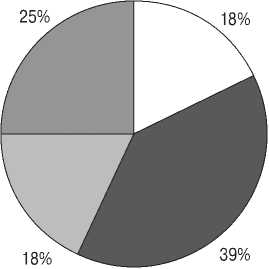
Рис. 3. Распределение итоговых оценок за дисциплину по группам

мости. Тогда преподаватель имеет возможность уделить больше внимания слабо успевающим студентам. Кроме того, разноуровневый характер заданий тематических тестов также ориентирован на различные группы студентов.

Для исследования эффективности системы непрерывного тестирования на протяжении 2012/ 2013 учебного года нами осуществлялся анализ результатов обучения по дисциплине «Линейная алгебра» студентов факультета экономики НИУ «ВШЭ» – Пермь. Было выявлено, что в силу различных причин (объективных и субъективных) студенты разделились на две группы: первая группа активно и регулярно работала с индивидуальной автоматизированной системой контроля знаний «Траектория», в то время как вторая группа работала не регулярно или практически не работала в этой системе. При этом начальный уровень математической подготовки студентов обеих групп был одинаковым, о чем свидетельствует средний бал за единый государственный экзамен по математике (для студентов первой группы он составил 70,93, для студентов второй группы – 68,55).

Таблица 2

Показатели качества знаний и успеваемости, %

Показатель	Первая группа	Вторая группа
Показатель качества знаний	86,4	56,8
Показатель успеваемости	100,0	81,8

На диаграммах представлено распределение итоговых оценок за дисциплину по группам (см. рис. 3). Все студенты первой группы справились с итоговой работой, а 18,2% студентов второй группы получили неудовлетворительные баллы. При этом больше половины студентов первой группы получили «отличные» оценки, а во второй группе таких студентов оказалось лишь 38,6%. По стандартным методикам рассчитывались лишь показатели качества знаний и успеваемости. Показатель качества знаний (качественная успеваемость) для группы студентов вычислялся по формуле:

ПКЗ = кол-во"^ кол-во"⁴" . 100%. общее кол-во учащихся

А показатель успеваемости (абсолютная успеваемость) для группы студентов вычислялся по формуле:

ПУ =

кол-во"5"+кол-во"4"+кол-во"3" общее кол-во учащихся

■100%.

Приведенные в табл. 2 значения показателей подтверждают, что студенты первой группы, которые на протяжении изучения дис- циплины «Линейная алгебра» самостоятельно работали с индивидуальной автоматизированной системой контроля знаний «Траектория», достигли более высоких результатов обучения, чем студенты, не использовавшие возможность самостоятельной подготовки и самоконтроля.

Таким образом, эффективность системы непрерывного тестирования можно считать доказанной. Следует также отметить, что ее использование оказалось очень удобным в условиях рейтингового подхода к обучению, принятого в НИУ «ВШЭ» – Пермь.

Предлагаемая система непрерывного тестирования позволяет осуществить интеграцию функ- ций процесса обучения (дидактическую, воспитательную и контролирующую), организовать самостоятельную работу студентов, повысить мотивацию обучения, учесть индивидуальные особенности студентов. Однако следует подчеркнуть, что она не заменяет, а дополняет классические подходы к обучению математическим дисциплинам.