Система поддержки моделирования социально-экономических процессов на основе платформы с открытым исходным кодом

Агентный принцип - одна из ключевых основ моделирования в социальных науках. В широком смысле он означает, что исследуемая система описывается через конкретных лиц, принимающих решения (ЛИР), которые действуют в соответствии со своими ценностями и интересами. В этой трактовке практически любые социальные и большинство экологических моделей являются агентными. В узком смысле под агентскими моделями понимаются модели, в которых описывается непосредственно решение агента, т.е. выбор им некоторых управляемых переменных в соответствии с установленными им самим критериями (этот выбор может быть полностью или ограниченно рациональным исходя из предусмотренной в модели асимметрии информации).

В общем виде логику построения агентной задачи можно описать так:

• 1)    Выбор ЛПР, критериев его выбора, факторов выбора и управлений.

• 2)    Формулировка условий (РОС, SOC) оптимальности выбора агента.

• 3)    Исследование агентной задачи.

• 4)    Совмещение моделей разных агентов через модели их взаимодействия (рынки, условия сохранения и т.д.).

• 5)    Получение функций поведения агентов (значения управления, функций зависимости управления от различных факторов, функции реагирования агента и т.д.).

Такие модели требуют не только адекватного описания принятия решения агентами и взаимодействий агентов, но и технологических средств работы с моделью. Описание нескольких агентов, поведение каждого из которых описывается условиями оптимальности или сценарием, необходимо объединить в сложную систему нелинейных соотношений, которую трудно записать без ошибок математическими выражениями на бумаге или на компьютере.

Построению крупных агентских моделей на практике мешают не столько сложности их аналитического решения (которое на определенном этапе исследования может быть заменено приближенными численными методами), сколько большая трудоемкость построения и отработки агентских моделей, и особенно мульти-агентских моделей (в которых предусмотрено наличие нескольких типичных агентов с однородным функционалом, но разными типовыми характеристиками: например, богатые и бедные домохозяйства).

Дополнительная трудность возникает, когда новые модели требуется создать в сжатые сроки, реализуя разные наборы предположений, и с целью решения разных проблем, на решение которых ориентированы модели. В связи с этим в моделях сложных систем часто можно увидеть, как полные агентские модели заменяются упрощенными функциями поведения, за которыми стоит микрообоснование с достаточно специфичными предпосылками.

Однако глобальные события, связанные с климатом и пандемией, поставили новые задачи перед математическим моделированием. Стало очевидно, что масштабные шоки невозможно рассчитать по статистическим моделям наблюдавшихся исторических данных, не содержавших ничего сравнимого с этим шоками. Резкие изменения внешних условий не могут быть описаны моделью, однозначно задающей логику поведения агента: необходима модель выбора, позволяющая показывать разную логику поведения при разных значениях факторов выбора (разные режимы модели). Для этого необходимы именно структурные агентские модели, причем для их ускоренного построения сам процесс моделирования должен быть в высокой степени автоматизирован. Для этого необходимы программные комплексы, способные:

• •    поддерживать моделирование на всех этапах, начиная с формальной записи модели и кончая представлением результатов расчетов;

• •    упрощать систему соотношений модели, сохраняя атрибуты уравнений и переменных;

• •    автоматически проверять корректность размерности переменных в соотношениях, что позволяет избежать ошибок и ошибочных расчетов из-за неправильной постановки задачи.

2.    Программное обеспечение для агент-ориентированного моделирования 3.    Система автоматизированной обработки агентских моделей

Существующие системы построены на коммерческих программных средствах, сильно ограничены жесткими предпосылками о характере модели [1-5]. Их инструменты предотвращения ошибок обеспечивают обратную связь лишь на уровне общей работоспособности модели, а не ее исправления. В связи с этим представляется, что дальнейшее развитие методов автоматической обработки агентских моделей способно существенно расширить возможности оперативного построения новых моделей сложных систем.

Авторы системы «Экомод» неоднократно отмечали особенности моделирования сложных систем, необзательно в экономике. Системы, способные к саморазвитию (например, как живой организм, биосфера, общество: технология, экономика, язык, культура), при моделировании проявляют сходные проблемы. Частные модели, не являющиеся частными случаями универсальной «супермодели», описывают отдельные аспекты исследуемой системы. При этом, в силу предпочтений авторов или заказчиков, эти конструкции оперируют разными наборами понятий и, будучи упрощенными описаниями, пренебрегают отдельными отклонениями от описываемых в них закономерностей [6, 7]. Подчас один коллектив исследователей использует разные конструкции при моделировании экономических подсистем - банка, международной торговли, внутреннего рынка, с различной детализацией или, наоборот, агрегированием показателей [8, 9]. Описание микросистем в прикладной модели может использовать большое число показателей, которые связаны несколькими соотношениями [10], что делает задачу анализа модели сложной с точки зрения выкладок.

Предпринят ряд попыток стандартизации моделей с целью возможности комбинировать разработки от разных моделей и адаптации к различным средам реализации. Для работы с моделями сложных систем была предложена каноническая форма и инструментальная система «Экомод» [6]. Каноническая форма - формализация модели в системе «Экомод» не привязана к инструменту автоматизации и является уникальной разработкой коллектива. Структурно-классификационные характеристики канонической формы в системе «Экомод» подразумевают специальное обозначение переменных, их индексацию, специальные записи в заголовках групп соотношений. Реализация системы в компьютерной алгебре Maple позволяла использовать атрибуты списков для того, чтобы записи соотношений и заголовки групп могли дополняться текстовыми комментариями. Модель, представленная в системе «Экомод» на Maple, выглядела удобно для пользователя, подробно описывая модель по блокам и демонстрируя символьную запись соотношений. Подход в рамках «Экомод» позволяет шесть уровней проверки корректности записи модели в канонической форме. Контроль 1-5 уровней формализован в виде проверки аксиом построения канонической формы [11, 12].

В статье [13] предлагается применение так называемых предметно-ориентированных онтологий для проектирования мультиагентных систем моделирования в микроэкономике. Под интеграцией авторы подразумевают комбинацию разнородных компонентов для крупномасштабных экспериментов с моделью, но при этом отмечают важность формализации для последующего повторного использования одной и той же части модели в других моделях или средах моделирования. В статье авторы предлагают подход, основанный на онтологии микроэкономики и связанные с ней ключевые параметры инструмента моделирования для ее реализации. Инструмент позволяет генерировать код для распределенной среды моделирования на основе агентов. Полученные результаты ориентированы на раз- работку имитационных моделей экономики и являются важным исследованием вопроса компонуемости моделей.

На сегодняшний денв существуют несколвко программных решений для поддержки моделирования. Самыми распространенным является DYNARE [5] на базе коммерческого продукта Matlab, а также менее распространенная, тоже носящая имя EcoMod, но разработанная другой группой и с другим подходом (статического общего равновесия экономики), также на Matlab [1-4]. Программное обеспечение для автоматизированной обработки моделей на основе платформ с открытым кодом начинает развиваться (как общего характера, см. Wolfram Alfa, так и специализированные, см. Dolo [15-17]). Однако подавляющее большинство таких систем направлены на автоматизированное исследование модели «как есть», а не на автоматизацию построения моделей.

Попытка формализации и стандартизации записи моделей в дискретном времени предпринята в виде Application Programming Interface (API), в библиотеке DOLO [15], написанной на языке Python. К сожалению, проект столкнулся с трудностями, так как был адаптирован к DSGE моделям со стохастической составляющей и на текущий момент не может работать с детерминированными моделями. Этот API, тем не менее, позволил формализовать сразу несколько моделей для возможности обобщения опыта идентификации большого круга прикладных моделей в работах [16, 17]. Показано удобство сравнения различных подходов к глубокому обучению с более традиционными итеративными методами подбора параметров модели, уже реализованными в Dolo.

Несмотря на все свои преимущества (система «Экомод» поддерживает базовые проверки и имеет аппарат для интеграции моделей разных агентов), она базируется на несвободной платформе Maple и не имеет специального интерфейса, рассчитанного на сторонних пользователей. Этим объясняется актуальность дальнейших работ по построению комплекса автоматизации агентного моделирования, который бы обладал следующими функциями:

• •    автоматизации ввода и вывода данных в общепринятом математическом формате (LaTeX);

• •    перекрестной проверки системы переменных, информирования пользователя о совершенных в ней ошибках;

• •    сведения балансов модели, выявления проблем незамкнутости и несвязанности взаимодействий между агентами;

• •    предложения типовых исправлений для выявленных проблем;

• •    автоматизированного вывода условий оптимальности.

3.1.    Архитектура системы

Принципиальные особенности автоматизированной обработки агентских моделей таковы. Прежде всего, описания отдельных агентов, включающее как формулы, так и их содержательное описание, объединяются в единую базу. Среди них выявляются сущности, выполняющие разную роль в агентской модели: описания агентских задач, переменных, целевые функции, уравнения/неравенства связи и уравнения переноса. Далее производится анализ размерности и исследование условий оптимальности агентов и упрощение получившейся системы. На разных этапах необходимо выявлять различные ошибки, информировать о них разработчика модели и предлагать типичные решения. Рассмотрим подробнее наиболее важные алгоритмы автоматизированной обработки агентской модели.

Создаваемая нами система является end-to-end LaTeX обработчиком агентских моделей, созданным на языке Python (рис. 1). Под обработкой подразумевается чтение и преобразование модели и вывод условий оптимальности. В качестве подсистем в ней присутствуют:

• 1)    Сериализатор и Десериализатор.

• 2)    Хранилище объектов.

• 3)    Ядро.

• 4)    Обработчик ошибок.

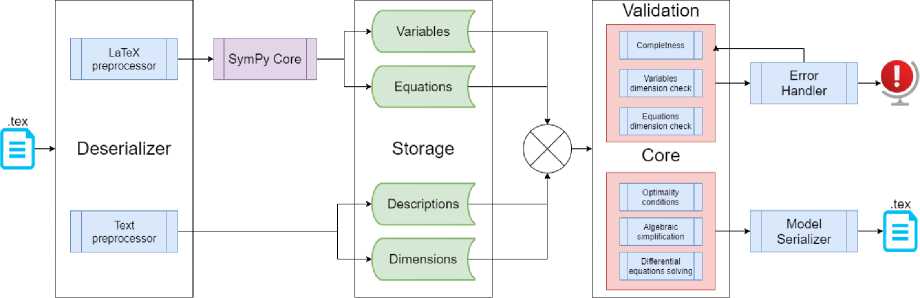
Рис. 1. Схема, системы «Экомод»

Входными данными, как и выходными, является .tex файлы (рис. 2), содержащие в себе математические формулы и их описания. Точкой входа, для системы является агентская модель (или несколько моделей), написанная синтаксисом LaTeX с соблюдением определенных правил. Структура, агентской модели зафиксирована, в виде, сродном с YAML. Результатом работы системы являются условия оптимальности для агентской модели (моделей) .

Также система, имеет функции пользовательской поддержки: классифицирует ошибки как критические или не критические и выдает пользователю соответствующую обратную связь. Критические ошибки вызывают прекращение работы системы, остальные ошибки не останавливают систему и выступают в качестве предупреждений.

Общие принципы обратной связи системы пользователю таковы:

• 1)    все ошибки делятся на. критические и гипотетические;

• 2)    при обработке ошибок предлагается их возможное решение;

• 3)    по каждой ошибке приводится как можно более точное указание на. место ее совершения в исходных данных.

3.2.    Требования к синтаксису

Так как LaTeX является языком разметки, а. не языком программирования, возникают проблемы с многозначностью входных данных. Поэтому в системе предусмотрены два. вида, ограничений на вход:

• 1)    Нативные ограничения синтаксиса. LaTeX.

Это требование использования специальных математических функций внутри LaTeX. Например, при записи логарифма, некоторой функции требуется явно указать

\log(C(t)), а не log(C(t))

То же самое касается экспоненциальной функции, синусов, косинусов и т.д.

• 2)    Обработка многосимвольных переменных.

Данное ограничение связано с многозначностью случаев определения выражений типа: Amm = m2. Например, оно может быть проинтерпретировано как А * m * m = m2 ^ A = 1, и как определение переменной Amm = m2.

Чтобы предотвратить данную многозначность, многосимвольные переменные (а при желании пользователя - все переменные) вводятся с помощью знака \:

\Amm = пГ{2}

• 3)    Обработка производных.

Для корректного чтения производных используется синтаксис:

\frac{dA(t)}{dt} - для первой производной

\frac{d\frac{dA(t)}{dt}}{dt} - для второй производной и т.д

• 4)    Обозначение фазовых переменных.

Для того чтобы переменная воспринималась системой как функция, требуется явно указать её аргументы, например:

\Amm(t) -- функция Amm от аргумента t, \Arnm -- переменная Amm

• 5)    Обозначение экзогенных переменных.

При соблюдении всех требований к синтаксису система классифицирует обрабатываемые переменные на четыре типа:

• 1)    варьируемые переменные;

• 2)    фазовые (динамические) переменные;

• 3)    экзогенные (информационные) переменные;

• 4)    калибровочные константы.

4.    Ключевые процедуры 4.1.    Сериализатор

При исследовании функционала рассматривается его зависимость от варьируемых переменных, в то время как экзогенные переменные (характеристики взаимодействий и других агентов) и калибровочные переменные обрабатываются как константы. При наличии ограничений на начальные или терминальные значения переменных, эти ограничения также вводятся в функцию Лагранжа с соответствующими двойственными множителями.

Поскольку внешние информационные переменные определяются из взаимодействия агентов, задача одного агента не решается аналитически в общем виде отдельно до построения всей модели. Для произвольных зависимостей цен, процентных ставок и других динамично меняющихся показателей конъюнктуры такое решение построить в принципе невозможно. Поэтому описание поведения отдельного агента в форме задачи оптимального выбора заменяется системой условий оптимальности. Как правило, экономический выбор из ограниченного множества альтернатив относится к сложному классу неавтономных задач со смешанными ограничениями [14]. В целях моделирования реалистичных траекторий экономических показателей, т. е. некоторым образом согласованных с задачей, функциях, мы считаем возможным воспользоваться простыми достаточными условиями оптимальности, если задача выпукла по управлениям и ограничения линейны по управлениям и фазовым переменным. В общем случае выводимые ниже условия можно считать только необходимыми. Как известно [18], траектория прямых (варьируемых) переменных оптимальна в задаче оптимального управления, если найдутся абсолютно непрерывные двойственные переменные к ограничениям-равенствам и измеримые неотрицательные двойственные переменные к ограничениям-неравенствам, которые вместе с переменными состояния и управления задачи образуют седловую точку функционала Лагранжа.

Рассмотрим подробнее ключевые процедуры (подсистемы), входящие в систему автоматизированной обработки агентских моделей.

Алгоритм работы сериализатора:

• 1)    Выделение YAML

Из исходного .tex файла выделяется tex-заголовок. Оставшаяся часть файла передаётся в сериализатор YAML. На выходе данного шага получаем .yarn! версию агентской модели, содержащую в качестве ключей LaTeX представления объектов модели, а в качестве значений - их описания и размерности.

• 2)    Обработчик LaTeX формул

• 3)    Текстовый обработчик

На данном этапе происходит формирование описания для уравнения и переменных. А также выявление размерностей переменных из описаний.

• 4)    Сборщик объектов

Задача агента:

Задача Агента

J = х/т*^ ехр(— Л ♦ <) log(c(<))rf/l Интегральная полезность

Лех

./: полезность

Активы агента:

Динамика *

^^ = г * x(t) — Q * e(t) Динамика капитала

ДО) — в: Начальный капитал

а: начальный капитал |гпЬ|

i(t): капитал агента |rub|

c(ty. вложения агента

Ограничения:

Ограничения

условие вложения капитала

условие неотрицательности вложений

Описание

г: процентная ставка |1/уеаг|

о; коэффициент ограничения вложений |гпЬ|

t: время |усаг|

Т: горизонтпланирования

Размерность

<5: коэффициент дисконтирования |1/усаг|

Q: нормировочный коэффициент |riib/year|

Рис. 2. Пример входных данных

INPUT:

Задача агента:

$J = 1/Т * \int _ 0~Т \exp(-\delta*t) \log(c(t))dt$: Интегральная полезность

$J$: полезность

Активы агента:

$\frac{dx(t)}{dt} = r*x(t)-Q*c(t)$: Динамика капитала

$x(0) = a$: Начальный капитал

$a$: начальный капитал [rub]

$x(t)$: капитал агента [rub]

$c(t)$: вложения агента

Ограничения:

$\sigma * c(t) < x(t)$: условие вложения капитала

$ c(t) \geq 0$ : условие неотрицательности вложений

$г$: процентная ставка [1/уеаг]

$\sigma$: коэффициент ограничения вложений [rub]

$t$: время [year]

$Т$: горизонт планирования [year]

$\delta$: коэффициент дисконтирования [1/уеаг]

$Ц$: нормировочный коэффициент [rub/year]

Во время сериализации могут возникнуть следующие ошибки, связанные с неверно написанным входным файлом:

е EcoModFileError - Критическая

Выявлена проблема со структурой файла.

е EcoModVariableError - Критическая

Выявлена проблема с чтением LaTeX формул и их интерпретацией.

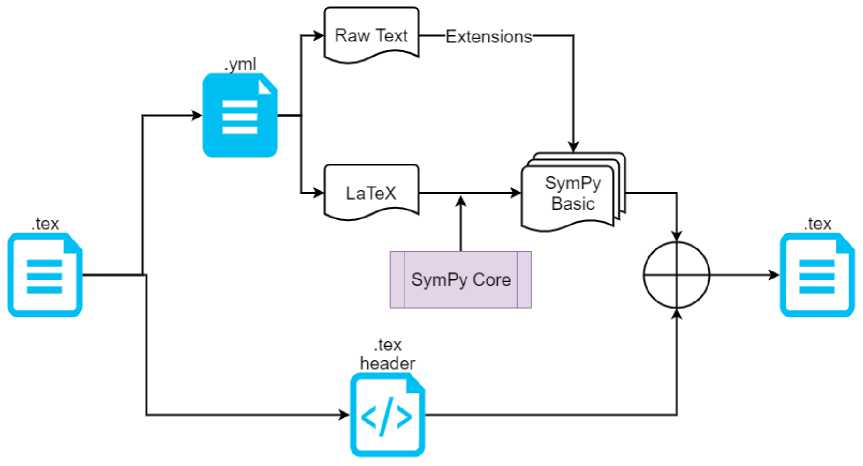
Рис. 3. Сериализатор в паре с десериализатором

4.2.    Хранилище

Хранилище системы представляет с собой локальное пространство объектов обработанной агентской модели, с которыми производятся дальнейшие преобразования и проверки. Основными компонентами хранилища являются: уравнения, переменные и их описания с размерностью. Все объекты модели хранятся в виде множества Sympy.Basic объектов.

4.3.    Ядро

Ядро системы состоит из двух частей - одна из них отвечает за валидацию данных, другая за их обработку и преобразование. Расскажем подробно про каждую из них.

Валидатор

Валидация данных агентской модели состоит из трёх проверок. Во время каждой из проверок система может выявить критичные и некритичные ошибки.

• 1)    Проверка на полноту

Проверка на полноту представляет собой обнаружение переменных, которые не были инициализированы в модели или переменных, которвіе инициализированы, но не используются в модели. В обоих случаях система смотрит на разницу между множествами символов, используемых в левых частях выражений модели, и множеством символов, представленных в правых частях равенств или неравенств. Первое множество получается на этапе сериализации модели, второе - с помощью встроенной функции Sympy.Core разложения выражений на составляющие компоненты.

• 2)    Проверка размерностей переменных

На этом этапе система еще не готова к проверке размерностей уравнений. Поэтому производится проверка наличия размерности у каждой переменной. Если во входном файле размерность переменной явно не указана, то по умолчанию она считается равной 1, а переменная - безразмерной.

• 3)    Проверка размерности уравнений

Для проверки размерностей был разработан соответствующий алгоритм (см. Algorithm 1) на SymPy. Основной идеей реализации на SymPy является возможность подстановки размерностей вместо переменных и дальнейшего упрощения полученного равенства или выражения уже в терминах размерностей. Более точно алгоритм выглядит следующим образом:

• Шаг 1:

Выделить специальные функции и запустить на них проверку размерностей, заменить вхождения на 1.

Шаг 2:

Заменить производные и интегралы функций на частное и произведение соответственно с сохранением размерности.

Шаг 3:

Заменить все вхождения переменных, на их размерности и упростить выражение.

Шаг 4:

Проверить на совпадение размерностей правой и левой частей выражения.

Во время валидации могут возникнуть следующие ошибки:

е MissedVariableError - Критическая

Система обнаружила пропущенную переменную в описании модели.

е ExtraVariableError - Не критическая

В модели есть переменные, которые не были использованы в уравнениях/неравенствах.

е MissedDimensionError - Не критическая

Есть переменные с пропущенной размерностью, по умолчанию считается безразмерной.

е DimensionCheckingError - Критическая

При проверке размерностей уравнений возникла ошибка.

Алгоритм 1 DimCheck: Проверка размерностей

1:    Expression ^ input() 2:    Special ^ getSpecialFuncs(Expression) 3:    for all Special do 4:    Result ^ DimCheck(Special) 5:    if Result is False then 6:       break 7:     else 8:       Expression ^ Expression.replace(Expression, 1) 9:    end if 10:    end for 11:    for Derivative ^ getDerivatives(Expression) do 12:    F, x, d ^ Derivative. values 13:     Result <---v xd

• 14:     Expression ^ Expression.replace(Derivative, Result)

• 15:    end for

• 16:    for Integral ^ getlntegrals(Expression) do

• 17:     F, x ^ Integral .values

• 18:     Result ^ F • x

• 19:     Expression ^ Expression.replace(Integral, Result)

• 20:    end for

• 21:    Result ^ Expression.subs({var : dim})

• 22:    if Result.lhs.dim == Result.rhs.dim then

• 23:     return True

• 24:    else

• 25:     return False

• 26:    end if

Преобразователь

После всех проверок можно работать с агентской моделью как с набором уравнений посредством интерфейса SymPy. Ниже приведён алгоритм вывода условий оптимальности:

• •    Разграничение выражений на дифференциальные, алгебраические и интегральные, на равенства и неравенства.

• •    Построение специальных функций: Лагранжиан, функция Лагранжа.

• •    Вывод и упрощение уравнения Эйлера.

• •    Построение условий оптимальности с помощью специальных функций.

4.4.    Десериализатор

Стандартный пакет функций SymPy предполагает импорт полученных выражений в виде формул LaTeX. Таким образом, за десериализатором остается лишь формирование словаря со стандартным набором выходных данных и склеивание с сохранённым на этапе сериализации .tex-заголовком.

Пример выхода для вышеописанной задачи представлен ниже. Здесв в качестве двойственных переменных представлены переменные p_agent1, p_agent2, Радепіз, причем имена для двойственных переменных (имеется в виду главный символ, здесв р) можно настраивать внутри системы.

• • Boundary conditions:

  ж(0) = а.

  
  

е Euler equation:

^^pagent3⁽i) ^{+ p}agent1^{(t) +} ~^^_^pagent3⁽t⁾ = 0.

• • Complementary slackness conditions:

⁽ (t⁾   ^(t)) ^pagent1^(t) A ⁰, ^c(t)pagent2^(t) A ^0,pagent1^(t) > ^0,pagent2^(t) A ^0.

• Lagrangean:

(dc(t) ~ ^(t)) pagentl

^(t) + ^Q^{c(t) -} rx^t) + |trr^(t)^

pagent3(t) +

+c(t)pagent2(t) +

Aoe ^5t log (c(t)) T

e Control optima condition:

(T (Qpagent3(t) + ^ Pagentl (t) + pagent2(t)) e^5t log (10) + ^) e ^5t T log (10)

e Lagrange function:

Aagentl ( —a + Ж(0)) +

⁺ I ⁽^^c(t) 0

— $(t)) pagentl(t) + ^Qc(t) - Tx(t) + ^^(t)^

pagent3(t) +

, x , x    A₀e ^5t log (c(t))

^+c(t)pagent2^(t) +-- T -------- ^^t.

• Transversality conditions: pagent3(0) = Aagentl, pagent3(T) = 0.

4.5.    Заключение

Автоматизация работы над агентскими моделями позволяет создавать комплексные модели сложных систем, которые базируются не на статистических закономерностях, а на логике оптимального выбора. Такие модели позволяют находить оптимальные решения даже в нестабильной внешней среде, когда социальная или техническая система в целом переключается между качественно различными режимами. Основным ограничением в развитии системных агентских моделей остается именно высокая вероятность возникновения ошибок в описании агентов, стремительно возрастающая при увеличении числа агентов.

Представленная архитектура системы автоматической обработки агентских моделей уже сейчас обладает всеми основными преимуществами системы «Экомод», одновременно обладая и главными преимуществами конкурирующих систем: реализация на общедоступных инструментах программирования (Pyton SymPy.Basic), возможность портативного развертывания на локальном устройстве без приобретения коммерческих лицензий.

Заложенные в систему инструменты обратной связи значительно превосходят существующие аналоги.

Это позволяет рассчитывать на большой потенциал практического применения системы, в первую очередь при построении моделей общего равновесия крупных систем (как в экономике, так и в других сходных задачах, которые могут быть формализованы теми же типами уравнений и неравенств).

Исследование выполнено за счет гранта Российского научного фонда № 22-21-00746.