Система поддержки принятия решений при управлении инновациями реструктурированного машиностроительного предприятия

В условиях радикальных изменений, происходящих в экономике России, снижения роли государства на экономической арене предприятия обороннопромышленного комплекса (ОПК) сталкиваются с проблемой, которая никогда раньше не возникала с такой остротой – проблемой поиска ресурсов для обеспечения военной промышленности. Выживают не столько предприятия, производящие высокотехнологичную продукцию, сколько умеющие адаптироваться к изменившимся условиям. Фактически ОПК, несмотря на «привилегированное» положение, проявляющееся в стабильных государственных закупках, постепенно начинает все больше и больше походить на обыкновенное производство потребительских товаров [1].

Возможным выходом из создавшейся ситуации является диверсификация производства военного сектора, которую можно представить себе как развитие технологий, позволяющих выпускать продукцию не только военного, но и гражданского назначения. Причем речь идет не только и не столько о продукции двойного назначения, а главным образом, о гражданской продукции, которую предприятия ОПК могут выпускать, применяя уже накопленный потенциал. Особенно следует выделить использование научнотехнического потенциала достижений НИОКР военного характера в сфере принципиально новых видов продукции, не имеющих аналогов и формирующих новый рынок сбыта.

Однако необходимо иметь в виду, что оптимальные пропорции между производством военной и гражданской продукции еще нужно определить. С одной стороны, слишком широкая диверсификация может повлечь за собой утрату конкурентных позиций на рынках военной продукции, с другой – ориентация на преимущественное производство военной продукции может повлечь утрату позиций в производстве конкурентоспособной гражданской продукции. Оптимальная интеграция гражданского и военного производства может значительно уменьшить издержки по производству новых видов вооружений, основанных на новейших технологиях, отработанных на гражданской продукции.

Таким образом, важнейшей задачей предприятий ОПК в современных условиях является преобразова- ние их систем управления с целью обеспечения координации усилий всех подразделений и служб для производства конкурентоспособной продукции как военного, так и гражданского назначения. В этой связи оптимальное распределение наиболее важных общих ресурсов реструктурированного предприятия ОПК между новыми коммерчески привлекательными производствами военной и гражданской продукции является актуальной научно-технической задачей.

Для реализации поставленных задач в изменяющихся условиях функционирования предприятия в целом и его подразделений целесообразно совершенствовать организационную структуру предприятия: создавать центр активного развития, переводить ряд подразделений на режим развитого хозрасчета – создавать центры финансовой ответственности (ЦФО), осуществлять работу по реинжинирингу биз-нес-процессов, созданию автоматизированной системы поддержки принятия управленческих и плановых решений, поставить «на поток» процесс формирования и реализации инновационных проектов с созданием соответствующей инфраструктуры [1].

Инновационная деятельность существующих и создаваемых центров финансовой ответственности определяет темпы реструктуризации предприятия и ее эффективность. ЦФО являются частью предприятия, работающего в рыночных условиях на рынках гражданской продукции. Их независимость от госзаказа и связанных с его выполнением проблем позволяет значительно ускорить их развитие.

Одновременно с этим ЦФО обладают значительным конкурентным преимуществом перед обычными коммерческими организациями: закрытая территория, уникальная специализация и самодостаточность инфраструктуры, высококвалифицированный персонал, общие с предприятием материальные ресурсы, уникальные экологические ресурсы (вода, воздух), наличие передового оборудования и технологий. Для обеспечения конкурентного преимущества ЦФО необходимо оптимально распределять финансовые и материальные ресурсы предприятия. Это, в свою очередь, требует разработки и внедрения эффективных моделей и методов поддержки принятия плановых решений при управлении инновационной деятельностью.

Полученные ранее результаты разработки математического, алгоритмического и программного обеспечения поддержки принятия плановых решений по распределению общих ресурсов при управлении инновациями на децентрализованных предприятиях ОПК в условиях адаптации к рыночным условиям позволяют осуществлять эффективное распределение общих ресурсов между подразделениями, что позволяет повышать гибкость и адаптивность при переходе к рыночным условиям хозяйствования.

Рассмотрим сначала модели рационального использования центрами финансовой ответственности общих дефицитных ресурсов, которыми в различных ситуациях могут быть электроэнергия, теплоснабжение, вода, трудовые ресурсы и т.п. Запасы таких ресурсов, которые могут быть использованы при планировании инновационной деятельности, определяются центром [2].

Объем p ij инновационной продукции j -го вида, выпускаемого i -м ЦФО зависит от затрат v ij дефицитных ресурсов:

p ij = f ij ( v ij ), v ij = ( v ij 1 , v ij 2 , . . ., v ijK ).

Затраты остальных (недефицитных) видов ресурсов полностью определяются технологией и фиксированы. Функции f_i j , естественно, считать монотонно возрастающими.

Кроме того будем считать, что эффективность затрат дефицитного ресурса падает с ростом его количества, т. е. функции f ij строго вогнуты. Центр имеет возможность распределять некоторый объем V k k -го ресурса – выбирать величины v ijk , удовлетворяющие ограничению nm

SS v j _Jt <  V , k = 1, 2, ..., K, i = 1 j = 1

максимизируя при этом прибыль от реализации выпускаемой продукции:

nm

SS df (v) ^ max i=1 j=1

Если решение о том, какие именно виды продукции планируются к выпуску, т. е. какие именно инновационные проекты будут реализовываться, уже принято, то полученная задача представляет собой обычную задачу нелинейного программирования и может быть решена стандартными методами.

Построим модель выбора инновационных проектов. Выбор инновационной программы определяется переменными x ij , которые равны единице, если принимается решение о реализации j -го инновационного проекта i -го ЦФО, и нулю – если такое решение не принемается.

Центр, получив информацию от всех ЦФО ( i = 1, …, m ), с учетом выделяемых ими денежных средств формирует оптимальный план нововведений, эффективный с точки зрения всего предприятия. Плановый объем денежных средств предприятия складывается из ресурсов отдельных ЦФО.

Найденный в результате решения этой задачи оптимальный план нововведений предприятия будет отличаться от оптимальных планов ЦФО. Отличие состоит в том, что общая прибыль будет, как правило, больше общей прибыли, полученной как сумма прибыли отдельных ЦФО. Это достигается за счет так называемого системного эффекта.

Более значительный эффект может быть достигнут при наличии у центра свободных средств, которые могут быть дополнительно направлены на реализацию инновационных проектов. При централизованном распределении средств получаемая модель имеет вид [2]

mn

S S П j ^ max;

i=1 j=1      ij mn

.^{S S}, cyxy < C ⁺ M ;

i = 1 j = 1

mn

.S Sn уху

i = 1 j = 1

-----------------< r ;

mn

. S ^S, cijxij i = 1 j = 1

Xy ={1,0} где Пij – плановая годовая прибыль на i-м ЦФО от внедрения j-го нововведения; cij – плановые годовые затраты на i-м ЦФО в j-е нововведение; С – плановый общий объем денежных средств всех ЦФО предприятия; xij – искомый параметр, показывающий, планируется ли к внедрению на i-м ЦФО j-e нововведение. Плановый объем денежных средств предприятия складывается из ресурсов отдельных ЦФО; М – денежные средства предприятия, которые оно может выделить на планы формирования нововведений ЦФО; r – допустимая средняя прибыль на 1 руб. затрат ресурсов (норма прибыли на капитал).

Дополнительное ограничение введено в модель с целью предупреждения его неэффективности с точки зрения внешних условий (процентных ставок банков, конкурентов и т. п.). Использование денежных средств центра увеличивает объем ресурсов, расширяет область нововведений, используемых ЦФО, что приводит к увеличению планируемой годовой прибыли.

Описанные модели позволяют осуществлять формирование инновационной программы при отсутствии зависимости ЦФО по технологической цепочке. В случае, когда такая зависимость имеет место, необходимо учитывать, что наращивание выпуска продукции в рамках реализации инновационного проекта одного ЦФО потребует наращивания выпуска продукции другими ЦФО, связанными с первым по технологии, причем это наращивание не имеет отношения к инновационным проектам этих ЦФО. Поэтому при централизованном распределении ресурсов необходимо решать следующую задачу [2]:

min( Q + i^ q .x ) ^ max

1SKm^1 j:1 i-Ч i m ni

S S ецх.. < C + M; i=1 j=1ij ij m ni z z i=1 J=1

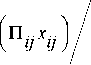
m ni

. zZ cjxj - r ^; i = 1 J = 1

xj = { 1,0 } ,

где cij – плановые годовые затраты финансовых средств i-го ЦФО на j-е нововведение, способствующее увеличению мощности предприятия; С – плановые годовые объемы финансовых средств, выделяемые ЦФО в план нововведений; М – плановый годовой объем финансовых средств, выделяемый центром в планы нововведений предприятий; Пij – плановый годовой объем прибыли, получаемый i-м ЦФО за счет увеличения объема выпуска продукции и снижения себестоимости ее изготовления; qij – плановый прирост годовой производственной мощности i-гo ЦФО за счет внедрения j-го нововведения, выраженный в выпуске конечной продукции; Qi – производственная мощность i-гo ЦФО, выраженная в выпуске конечной продукции данного наименования на конец отчетного периода времени; r – допустимая средняя прибыль на 1 руб. затрат (норма прибыли на капитал). Реализация получаемого оптимального решения обеспечивает последовательное выравнивание производственных мощностей предприятия.

Объединяя построенные модели, с учетом общих ограничений и необходимости учета риска инновационных проектов, получаем следующую модель:

mn

Z EH; ,x ^ max;

i=1 J=1 ij ij ni min( Q + Ya x ) ^ max

1

Z Z RiiX.. ^ min; i = 1 j = 1 ¹ ij

m

Z i=1

n

Z CijXij < C ⁺ M ; j = 1

mn

.Z ^Z." y^xy i = 1 J = 1

mn

У У .^Z, ^Z, J J I = 1 J = 1

< r ;

nm

ZZ v ,k_t ⁽ X j ) <  V , k = 1, 2, ^, K, i = 1 J = 1

xjj ={1,0} , где Rij – экспертная оценка рискованности соответствующего инновационного проекта, vijk(xij) – результат решения задачи оптимизации распределения общих дефицитных ресурсов для инновационных проектов, включенных в инновационную программу.

Таким образом, для повышения обоснованности принятия решений по распределению общих ресурсов при управлении инновационными процессами реструктурированного предприятия ОПК необходимо в общем случае решать задачу оптимизации с булевыми переменными, тремя критериями, алгоритмически заданными, и двумя линейными ограничениями. Точных эффективных методов решения таких оптимиза- ционных задач в настоящее время не существует. Следовательно, необходимо разрабатывать приближенные методы решения таких задач.

Для решения поставленной проблемы были применены эволюционные алгоритмы, представляющие собой стохастическую оптимизационную процедуру, имитирующую процессы естественной эволюции [3]. На основе математической модели и многоагентных стохастических алгоритмов была разработана система поддержки принятия решений при управлении реальными инвестициями реструктурируемого предприятия (см. рисунок).

Для учета ограничений оптимизационной задачи применялись соответствующие механизмы.

Метод статических штрафов предполагает формирование для каждого ограничения семейства интервалов, которые определяют соответствующие коэффициенты штрафов.

Метод динамических штрафов , в отличие от предыдущего метода, вычисляет штрафы динамически, т. е. в зависимости от степени нарушения ограничений.

Метод «смертельных» штрафов заключается в отсечении («убийстве») недопустимых точек, т. е. эти точки не принимают более участия в воспроизводстве. Для некоторых задач этот простой метод может давать хорошие результаты. Для использования данного метода необходимо инициализировать стартовую популяцию допустимыми значениями.

В методе адаптивных штрафов штрафные функции зависят не только от номера итерации, но и от количества попаданий лучшего представителя популяции на каждом шаге в допустимую или недопустимую области.

Однако эволюционные алгоритмы имеют множество настраиваемых параметров, от которых зависит эффективность их работы. Поэтому был проведен сравнительный анализ эффективности ГА на множестве тестовых задач безусловной и условной оптимизации.

На основе проведенных экспериментов установлено, что в большинстве случаев наиболее эффективным (надежным и быстрым) оказывается генетический алгоритм с равномерным скрещиванием. Равномерное скрещивание допускает модификацию, использующую многих родителей и организации селективного давления на этапе скрещивания, чего нет у стандартного генетического алгоритма. Рассматривались следующие модификации равномерного скрещивания:

– равномерное пропорциональное скрещивание – вероятность того, что ген именно этого родителя будет передан потомку пропорционально его пригодности;

– равномерное ранговое скрещивание – родители ранжируютя и вероятность того, что ген этого родителя перейдет потомку, пропорциональна рангу претендента, а непригодности;

– равномерное турнирное скрещивание – организуется турнир среди родителей, победитель которого передает свой ген.

й# 1ПР формирования инвестиционных программ

Файл Алгоритм Анализ

Ц| Настр

Введите к

Р Задать по

Введите количество ЦФО:

Принять

Отменить

Генетический алгоритм | Стайный алгоритм Выбор алгоритма |

У# 1ПР формирования инвестиционных программ

Файл Алгоритм Анализ

Генетичес

Настр

С* Стайный а

Введите С:

в противном случае

Введите Ы:

WA л® А ^й

Настройки штрафа

Коэффициент штрафа:X® (Ct)

I • на t-ой итерации

Настройки штрафа

Звените Ь2:

выделяемых центральной компанией на инвестиционный портфель:

Ограничения на среднюю норму прибыли на капитал:

Чтобы изменить предыдущие параметры - нажмите "Назад", чтобы продолжить • нажмите "Далее"

Рабочие окна системы поддержки принятия решений

Генетический алгоритм Стайный алгоритм | Выбор алгоритма |

Алгоритм

Количество частиц:

Количество поколе ОД |ас

Коэффициент обуче Генетический на собственном оп

_ Тип селекции

Коэффициент обуче

Щ СППР формирования инвестиционных программ

Файл Алгоритм Анализ

.оличество поколений

.оличество прогонов:

Коэффициент штрафа: ад (с g t • на t-ой итерации b ■ лучший индивид

Все готово для формирования портфеля, чтобы начать ■ нажмите "Анализ •> Формирование портфеля", если хотите изменить предыдущие параметры - нажмите

Це:-: 43: Производство сжиженного и газообразного кислорода

ПТПП: Производство геополотна

ПТПП: Производство тканой полипропиленовой продукции

Це:-: 40: Комплектация ГБ О ГИГ

Планируемая прибыль: 117,2

Объем капиталов: 239,8

Т ребуемое вложение: 18,8

Затраты на ПТНП: 80,1

Затраты на ПЭП: 83,1

Затраты на Цех 43: 42,5

Затраты на ПТПП: 33,6

Затраты на Цех 40: 0,5

Оценка рискованности: 1,98

Оценка рентабельности: 12,3013533738092

ип штрафа

Адаптивный ~^~|

/ Применять "лечение"

оличесвто индивидов:

Применять поведенческую память

оличество поколений

Введите а::

если Ь допустим к раз

если Ь недопустим к раз

Была разработана программная система решения задач условной и безусловной оптимизации стандартным генетическим алгоритмом и генетическим алгоритмом с оператором модифицированного скрещивания, и с ее помощью были проведены исследования эффективности предложенного подхода.

При анализе было выявлено, что равномерное пропорциональное и равномерное турнирное скрещивание не увеличивают эффективность алгоритма. Равномерное ранговое и равномерное равновероятное скрещивание более эффективны, чем остальные виды, включая одноточечное и двухточечное. Наиболее эффективное количество родителей – 6.

По результатам исследования СППР формирования инновационных программ были получены следующие результаты: равномерное турнирное скрещивание не увеличивает эффективность алгоритма, равномерное равновероятное и равномерное пропорциональное скрещивание имеют примерно одинаковую эффективность, в среднем более высокую, чем одноточечное и двухточечное, равномерное ранговое скрещивание более эффективно, чем остальные виды скрещивания. Наиболее эффективное количество родителей – 7. Другие настройки ГА наиболее эффективные в среднем: тип селекции – турнирная селекция с размером турнира 5, тип мутации – средняя мутация: не использовать элитизм, не применять «лече- ние» с «поведенческой» памятью, метод учета ограничений – динамические штрафы.

В окончательном варианте предлагаемой СППР по умолчанию установлены наиболее эффективные настройки генетического алгоритма, однако при желании и наличии соответствующих навыков пользователь имеет возможность изменить параметры алгоритма.

СППР прошла успешную апробацию при решении реальной задачи формирования инновационной программы Химзавода-филиала ОАО «Красмаш» (6 – ЦФО, 32 – инновационных проекта, 6 общих дефицитных ресурсов). Данная система может быть рекомендована к применению на других предприятиях и в других отраслях.