Системно-структурный подход к преподаванию математики в вузе

граф; программа курса "Высшая математика

В работе предлагается один из вариантов построения модели преподавания математики как открытой сложной развивающейся системы.

Процесс обучения математике является весьма сложным и многогранным. Существует мнение [1], что для успешного преподавания математики в вузе нужны два качества: хорошее знание предмета и хорошее знание языка, на котором ведется преподавание. Конечно, указанные требования к преподавателю являются совершенно необходимыми, но часто недостаточными для эффективного учебного процесса.

Трудности при обучении математике возникают уже при подготовке к лекционным и практическим занятиям, они связаны с подбором материала, выбором принципов обучения, доступностью преподаваемого материала, полнотой и глубиной его изложения.

По мнению автора, эти трудности можно устранить с помощью системноструктурного подхода к преподаванию математики в вузе, например, для студентов

специальностей естественно-научного цикла [3].

Для системно-структурного подхода характерны упрощение изучаемых сложных объектов, процессов и их формализация . Под формализацией при этом понимается упорядоченное и специальным образом организованное представление о методологических подходах к изложению материала, дидактических единицах и модулях .

В системно-структурном подходе наряду с понятием системы решающую роль играет понятие структуры [4]. Из множества имеющихся на сегодняшний день определений можно выделить достаточно общие определения структуры как внутреннего устройства чего-либо и как системы устойчивых связей элементов. В целях нашего изложения под структурой будем понимать способ устойчивого функционирования системы.

Выявление связей, изучение взаимодействия и соподчиненности составных частей системы позволяют говорить об иерархи ческой структуре системы. Одним из формальных математических методов такого анализа является теория графов, в частности, использование графов типа " дерево ".

Построение графа процесса преподавания математики является сложным и определяющим этапом моделирования.

Сложность этого этапа - в отсутствии строгих формальных процедур его реализации, что иногда позволяет относить его скорее к искусству ( эвристике ), чем к науке.

Предлагается следующий эвристический подход к решению поставленной задачи.

Выделим пять методологических подходов (методов) ( исторический , познавательный , прикладной , предметный и топологический), в соответствии с которыми можно изучать математику. В историческом плане математику условно разделим на элементарную , высшую и современную .

Элементарная математика пользуется теми понятиями (абстракциями), которые сложились исторически до появления высшей математики. Элементарная математика охватывает в основном арифметику (элементарную теорию чисел), элементарную алгебру, элементарную геометрию, тригонометрию.

Под высшей математикой обычно понимают совокупность математических дисциплин, возникших примерно в середине шестнадцатого века и входящих в учебные планы дисциплин высших учебных заведений. Как правило, это линейная алгебра, аналитическая геометрия, математический анализ и теория дифференциальных уравнений.

Современную математику условно определим как математический комплекс, включающий в себя все разделы элементарной, высшей математики, а также математические дисциплины и теории, разработанные с пятидесятых годов прошлого века до наших дней.

Познавательный подход представим следующими направлениями: прагматизм , конструкционизм , интуиционизм , формализм , классицизм [2].

Основной идеей прагматизма в математике является то, что математика должна быть лишь инструментом при решении проблем и задач, которые возникают в различных жизненных ситуациях, в процессе практической деятельности человека в постоянно меняющемся мире.

Конструктивная математика (конструк-ционизм) - близкое к интуиционизму течение в математике, изучающее конструктивные построения. Согласно критерию конструктивности "существовать - значит быть построенным ". Критерий конструктивности - более сильное требование, чем критерий непротиворечивости.

Интуиционизм предполагает в основании математики интуиционистскую логику, более ограниченную в средствах доказательства. Интуиционизм отвергает доказательство от противного, многие неконструктивные доказательства становятся невозможными, а многие проблемы теории множеств - бессмысленными (неформализуемыми).

Согласно формализму математика характеризуется скорее своим методом, нежели предметом изучения.

Классицизм означает использование аппарата классической - (высшей) - математики (математики конца XIX - начала XX в.).

Прикладной подход представим двумя направлениями - чистая и прикладная математика.

К "чистой математике" относят ариф метику, алгебру, функциональный анализ, анализ бесконечно малых величин, а также дифференциальное исчисление, интегральное исчисление и вариационное исчисление, те орию чисел, геометрию, тригонометрию и др.

Прикладная математика - область мате матики, рассматривающая приложения математического знания в других сферах деятельности. Примерами такого применения являются численные методы, оптимизация и ис следование операций, моделирование сплошных сред, теория информации, теория игр, теория вероятностей и статистика, финансовая математика, комбинаторика, теория гра фов и др.

Предметный подход - классическая, конечная, вычислительная, компьютерная и асимптотическая математика.

Топологический подход представим дискретной и континуальной математикой.

Основные определения и понятия двух последних подходов и их разделов можно найти в многочисленных литературных источниках, посвященных философским и методологическим вопросам математики.

Представим координацию и субординацию выделенных разделов и подразделов в виде графа (рис.1).

Рассмотрим применение системноструктурного подхода к формированию программы начального курса математики на примере рабочей программы данного курса для студентов биологических специальностей.

элементарная

Исторический

высшая современная прагматизм конструкционизм интуиционизм

Познавательный '

1------------------ формализм классицизм

классическая конечная

- Предметный I—■

вычислительная

компьютерная

асимптотическая

__________________ дискретная

Топологический I —континуальная

Рис. 1

Содержание курса (п рограмма ) приведено далее.

Раздел 1. Линейная алгебра

Тема 1. Матрицы и действия над ними

Понятие матрицы. Типы матриц. Сложение матриц. Умножение матрицы на число. Умножение матриц. Транспонирование матриц.

Тема 2. Определители

Квадратные матрицы. Понятие и определения определителей квадратных матриц. Вычисление определителей 2, 3 и 4-го порядков. Вычисление обратной матрицы.

Тема 3. Системы линейных алгебраических уравнений; методы их решения

Определение системы алгебраических линейных уравнений. Основные понятия и определения. Матричный метод решения систем линейных уравнений. Методы Крамера и Гаусса решения систем линейных уравнений. Ранг матрицы. Теорема Кронекера–Капелли.

Раздел 2. Аналитическая геометрия на плоскости

Тема 4. Метод координат на плоскости

Декартовы прямоугольные координаты на плоскости. Простейшие задачи на метод координат (расстояние между двумя точками на плоскости и деление отрезка в данном отношении).

Тема 5. Полярная система координат

Декартовы прямоугольные координаты на плоскости. Простейшие задачи на метод координат (расстояние между двумя точками на плоскости и деление отрезка в данном отношении).

Тема 6. Уравнение линии на плоскости

Уравнения линии на плоскости относительно декартовой прямоугольной системы координат на плоскости.

Тема 7. Прямая линия. Взаимное расположение прямых

Уравнение прямой с угловым коэффициентом. Уравнение прямой, проходящей через данную точку в данном направлении. Уравнение прямой проходящей через две заданные точки. Уравнение прямой в отрезках. Общее уравнение прямой. Угол между двумя прямыми на плоскости. Условия параллельности и перпендикулярности двух прямых.

Тема 8. Кривые второго порядка

Общее уравнение кривых второго порядка. Канонические уравнения окружности, эллипса, гиперболы, параболы. Построение кривых второго порядка по их каноническим уравнениям .

Раздел 3. Высшая алгебра

Тема 9. Комплексные числа

Тема 10. Многочлены

Раздел 4. Введение в математический анализ

Тема 11. Функция одной переменной

Понятие функции одной переменной. Область определения и область значений функции. Способы задания функции одной переменной. Элементарные функции, их свойства и графики.

Тема 12. Предел функции

Понятие предела переменной. Определение предела функции. Раскрытие основных неопределенностей. 1-й и 2-й замечательные пределы.

Тема 13. Непрерывность функции

Определение непрерывности функции в точке и на отрезке. Свойства непрерывных функций.

Тема 14. Производная функции

Определение производной данной функции. Непосредственное вычисление производной. Свойства производных. Таблица основных производных.

Тема 15. Исследование функций с помощью производных

Возрастание и убывание функции. Достаточные условия монотонности функции. Экстремум функции. Необходимые и достаточные условия экстремума функции. Выпуклость, вогнутость, точки перегиба графика функции. Достаточные условия выпуклости, вогнутости, точек перегиба.

Тема 16. Построение графика функции

Асимптоты графика функции. Общая схема исследования функции и построения ее графика. Пример исследования функции и построения ее графика.

Рассматриваемая программа должна характеризоваться следующими модулями: высшая математика; классицизм; чистая и прикладная математика; классическая математика; континуальная математика. То есть программа курса математики для студентов-биологов должна содержать основные разделы курса высшей математики, в познавательном плане указанные разделы должны преподаваться с позиций классицизма, в прикладном плане необходимо использовать "чисто" математические и прикладные примеры и задачи. В плане предметном и топологическом необходимо использовать классический подход кон-

Граф представим узлами-разделами программы: "Линейная алгебра", "Аналитическая геометрия", "Высшая алгебра", "Введение в математический анализ".

Содержание каждого из этих разделов представлено соответствующими графами (рис. 3, 4, 5, 6), "глубина" и степень формализации которых в зависимости от поставленной цели могут варьироваться. Ограничимся представлением графов "Линейная алгебра", "Высшая алгебра", "Ведение в математический анализ" в виде 2-уровневых графов.

Граф "Аналитическая геометрия" представим 6-уровневым графом-деревом, "листья" которого будут символами тематических расчетных формул.

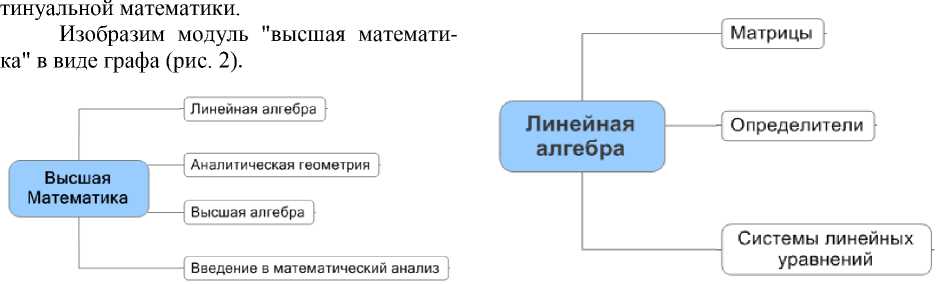
Рис. 3

Рис. 2

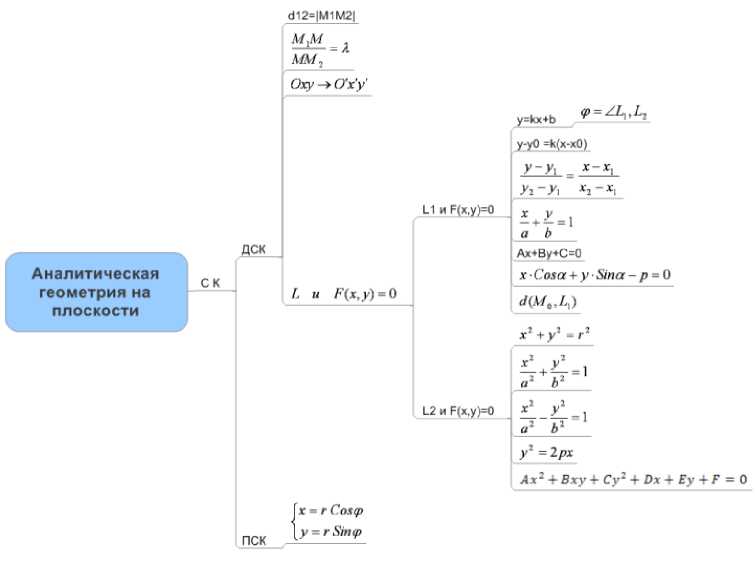
Рис. 4

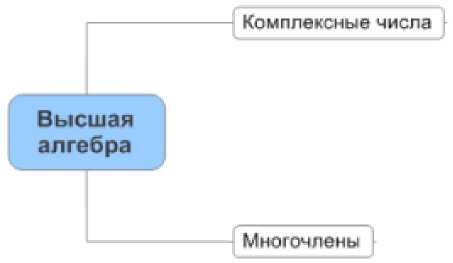
Рис. 5

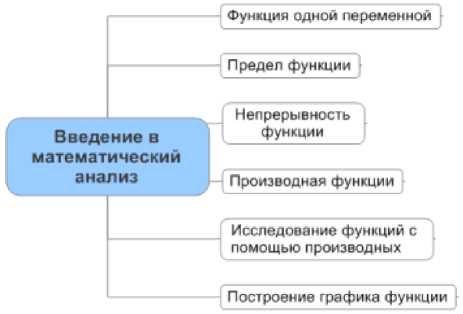
Рис. 6

Основными достоинствами графического представления программы курса математики являются высокая информативность представления материала, подлежащего изучению, наглядность и декомпозируемость разработанных конструкций, принципиальная воз- можность целостного восприятия программы, удобство интерпретации и обработки на средствах вычислительной техники.

Таким образом, системно-структурный подход к преподаванию математики позволяет:

– структурировать процесс разработки рабочей программы читаемого курса,

– представлять в наглядном, компактном виде основные разделы разрабатываемой программы,

– в зависимости от специализации и подготовленности слушателей, целей читаемого курса и других факторов вычленять ту или иную его ветвь,

– дополнять необходимыми разделами программу (расширять граф) и детализировать определенные разделы (углублять граф),

– в перспективе – автоматизировать этапы разработки и реализации учебных образовательных программ.