Системный анализ процессов восстановления оксидов железа в атмосфере водяного газа в присутствии углерода

В работе [1] обсуждались некоторые особенности представления метастабильных параметров равновесия оксидов железа с водяным газом в виде пространственной диаграммы. Метастабильность анализируемых равновесий определяется тем обстоятельством, что при расчетах сознательно игнорировалось присутствие в качестве самостоятельной фазы сажистого углерода, появление которого возможно в результате протекания реакции 2CO = C + CO2 при некоторых концентрациях СО и при температурах выше 955 К. В настоящей статье излагаются результаты расчетов равновесных параметров систем:

Fe 3 O 4 –Fe–СО–СО 2 –Н 2 –Н 2 О–C при температурах ниже 850 К;

Fe 3 O 4 –FeO–СО–СО 2 –Н 2 –Н 2 О–C при температурах выше 850 К;

FeO–Fe–СО–СО 2 –Н 2 –Н 2 О–C при температурах выше 850 К.

Предполагается присутствие в таких системах большого избытка углерода в качестве устойчивой самостоятельной фазы, поэтому образование сажистого углерода не должно сказываться на равновесных параметрах систем.

Сначала определим параметры равновесия водяного газа с углеродом в отсутствии оксидов железа. В этом случае при расчетах параметров равновесного состояния следует учитывать две независимые реакции:

H 2 + CO 2 = H 2 O + CO,

A r G' T (1) = 36 580 - 33,465 T , Дж;          (1)

C + CO 2 = 2CO,

A _rG°_T (2) = 172140-177,7 T , Дж.           (2)

Трехкомпонентная двухфазная система СО–СО2– Н2–Н2О–C при фиксированных температуре и давлении имеет одну степень свободы. Расчеты равновесных концентраций газа базируются на трех уравнениях:

^x CO ^x H₂O    ^x CO ^x CO₂

K1 =           =     ;      ;(3)

^x CO₂ ^x H₂    ^x H₂ ^x H₂O

K2 = xO- P ;(4)

^x CO₂

2 X = XCO + x H2O + x CO2 + x H2 = 1, где xi – молярные доли компонентов газовой фазы;

K1 и K2 – константы равновесия реакций (1) и (2). Такая система трех уравнений с четырьмя неизвестными имеет множество решений. Для получения частного варианта необходимо задаться каким-либо параметром равновесного состояния системы. Наиболее простые расчетные выражения получаются, если задаться концентрацией xCO или суммой концентраций xCO + xCO2 . Например, задавшись величиной xCO , из уравнения (4) рассчиты- ваем xCO2 , xCO + xCO2 и отношение xCO xCO2 . Затем по уравнению (3) вычисляем отношение xH2xH2O. И, наконец, по условию нормировки (5), используя xCO + xCO2 , рассчитываем xH2 и xH2O. Некоторые результаты таких расчетов представлены в табл. 1. Аналогичные расчеты с использованием заданных величин xCO + xCO2 приводят к таким же результатам (табл. 2 и 3).

Таблица 1

Параметры равновесия системы Н 2 –Н 2 О–СО–СО 2 –С при заданных температурах и давлении 1 атм

Т = 700 К					Т = 1000 К					Т = 1500 К
x CO	x CO2	x H2O	x H 2	x CO + x H 2	x CO	x CO2	x H2O	x H 2	x CO + x H 2	x CO	x CO2	x H2O	x H 2	x CO + x H 2
0,001	3,7 ⋅ 10–2	0,275	0,720	0,721	0,05 ∗	1,28 ⋅ 10–3	1,64 ⋅ 10–2	0,932 ∗	0,982	0,05	1,3 ⋅ 10–6	7,3 ⋅ 10–5	0,95	1,00
0,003	3,3 ⋅ 10–2	0,515	0,450	0,453	0,10 ∗	5,12 ⋅ 10–3	3,05 ⋅ 10–2	0,864 ∗	0,964	0,10	5,1 ⋅ 10–6	1,4 ⋅ 10–4	0,90	1,00
0,005	9,1 ⋅ 10–2	0,593	0,311	0,316	0,20 ∗	0,0205	0,0513	0,728 ∗	0,928	0,20	2,0 ⋅ 10–5	2,5 ⋅ 10–4	0,80	1,00
0,007	0,179	0,592	0,222	0,229	0,30 ∗	0,0461	0,0625	0,591 ∗	0,891	0,30	4,6 ⋅ 10–5	3,2 ⋅ 10–4	0,70	1,00
0,010	0,366	0,495	0,130	0,140	0,40 ∗	0,0819	0,0639	0,454 ∗	0,854	0,40	8,2 ⋅ 10–5	3,7 ⋅ 10–4	0,60	1,00
0,011	0,443	0,441	0,105	0,116	0,50**	0,1281**	0,0557	0,316 ∗	0,816	0,50	1,3 ⋅ 10–4	3,8 ⋅ 10–4	0,50	1,00
0,012	0,527	0,379	0,083	0,095	0,60 ∗	0,184	0,0376	0,178 ∗	0,778	0,60	1,9 ⋅ 10–4	3,7 ⋅ 10–4	0,40	1,00
0,013	0,618	0,307	0,062	0,075	0,70 ∗	0,251	0,0097	0,0393 ∗	0,740	0,70	2,5 ⋅ 10–4	3,2 ⋅ 10–4	0,30	1,00
0,014	0,717	0,227	0,042	0,056	0,72 ∗	0,266	2,92 ⋅ 10–3	0,0115 ∗	0,730	0,80	3,3 ⋅ 10–4	2,5 ⋅ 10–4	0,20	1,00
0,0164	0,9836	0	0	0,0164	0,7283	0,2717	0	0	0,7283	∼ 1	∼ 0	∼ 0	∼ 0	∼ 1,00

Примечания: * концентрации нанесены на изотерму 1000 К на рис. 1 и 2; ** концентрации использованы для расчетов табл. 2; последняя строка – параметры равновесия системы СО–СО2–С.

Параметры равновесия системы Н 2 –Н 2 О–СО–СО 2 –С при 1000 К

Параметры равновесия системы Н 2 –Н 2 О–СО–СО 2 –С ( x _CO + x _CO2 = 0,5 )

Таблица 2

g = x CO + x CO 2	1	0,75	0,6281	0,5	0,25
x CO	0,728	0,5785	0,5000	0,4127	0,2242
x CO2	0,272	0,1715	0,1281	0,0873	0,0258
x H2O	0	0,0423	0,0557	0,0635	0,0549
x H 2	0	0,2077	0,3162	0,4365	0,6951

Таблица 3

Т , К	700	800	900	1000	1093	1100	1200	1300	1400
x CO	0,0116	0,0689	0,2299	0,4127	0,4797	0,4819	0,4960	0,4989	0,4997
x CO2	0,4884	0,4311	0,2701	0,0873	0,0203	0,0181	0,0040	0,0011	3,45 ⋅ 10–4
x H2O	0,4076	0,2943	0,1657	0,0635	0,0202	0,0185	0,0057	0,0020	8,33 ⋅ 10–4
x H 2	0,0924	0,2057	0,3343	0,4365	0,4798	0,4815	0,4943	0,4980	0,4992
x CO + x H2	0,104	0,2746	0,5642	0,8492	0,9595	0,9634	0,9903	0,9969	0,9989

Параметры равновесий в системе Н 2 –Н 2 О– СО–СО₂–С можно представить пространственной диаграммой в координатах Т – x CO – x H 2 (рис. 1). Фигуративные точки на поверхности MLFE определяют возможные составы водяного газа, равновесного с графитом. Образующими этой криволинейной поверхности являются изотермические прямые линии. Линии изотермических сечений поверхности MLFE , которые могут быть представлены проекциями на плоскость x CO – x H 2 , приведены на рис. 2. Для подтверждения линейности изотермических сечений на изотерму 1000 К и на рис. 1, и на рис. 2 нанесены точки, координаты которых представлены в табл. 1–3.

По поводу рис. 2 следует сделать такие замечания. Во-первых, точки на изотермах показывают множество возможных концентрации Н2 и СО, другими словами, координаты точек на изотермах характеризуют возможные сочетания xCO и xH2 в равновесном с графитом водяном газе. Во-вторых, изотермы соединяют точки с координатами xCO = 0, xH2 = 1 с точками, координаты которых определяют xCO - молярную долю СО в равновесном газе в системе СО–СО2–С – линия EF на рис . 1 есть кривая Белла – Будуара, координаты точек которой определяются точками пересечения изотерм с осью абсцисс на рис . 2. Таким образом, при заданной температуре xCO в водяном газе изменяется в пределах от 0 до xCO , тогда как xH2 - в пределах от 0 до 1. В-третьих, концентрации СО2 и Н2О определяются отрезками Af и Ag на рис . 2. Очевидно, что nA + Ag = xH2 + xH2O и mA + Af = xCO + xCO2 . И, наконец, с повышением температуры сумма xH2O+ xCO2 стремится к нулю, а сумма xH2 + xCO – к единице (см. табл. 3), то есть при высоких температурах (выше ~ 1100 К) водяной газ в присутствии графита характеризуется максимальной восстановительной способностью.

При анализе равновесий систем «оксиды железа – водяной газ – графит» следует учитывать, что при заданных давлении и температуре эти системы нонвариантны и состав газовой фазы должен быть строго фиксирован. Например, для определения параметров равновесия пятикомпонентной пятифазной системы Fe₃O₄-FeO-Fe _a -СО-СО 2 -Н 2 -Н 2 О-C при 850 К следует рассчитывать равновесия трех независимых реакций:

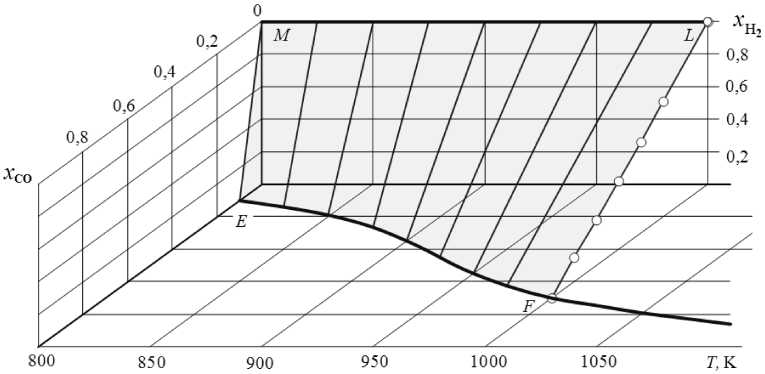
Рис. 1. Параметры равновесия водяного газа с графитом

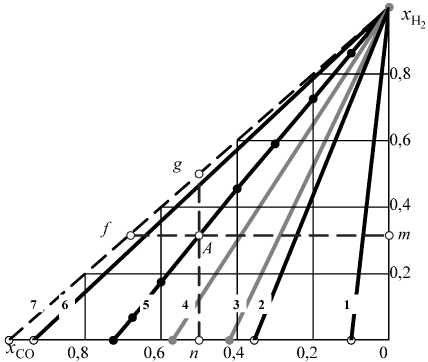
Рис. 2. Возможные концентрации газов-восстановителей в системе Н 2 –Н 2 О–СО–СО 2 –С: 1 – 800, 2 – 900, 3 – 917, 4 – 955, 5 – 1000, 6 – 1100, 7 - выше 1300 К ( x CO + x H 2 = 1 )

Fe₃O₄ + CO = 3FeO + CO 2 ,

A G T (6) = -10 034 - 38,635 T In T +

+271,78T, Дж;(6)

FeO + H₂ = Fe_a + H₂O,

ArGT(7) = 14 799-8,465T, Дж;(7)

C + CO₂ = 2CO,

ArGT (2) = 172140 -177,7T, Дж.(2)

Система четырех уравнений с четырьмя неизвестными:

FeO + CO = Fe_a + CO₂,

A r G T (12) = -21 785 + 25 T , Дж, Т < 1185 К; (12) FeO + H₂ = Fe_a +H₂O,

A _rG°_T (13) = 14 799-8,465 T , Дж, Т < 1185 К; (13)

xCO2

K 6 =      ; K 7 = xCO

K 2 = x^ P ; S x_t = 1

xCO2

имеет единственное решение:

x CO =

K 6 K 2

P

^x CO₂

K 6² K 2_;

P ^;

C + CO₂ = 2CO,

ArGT (2) = 172140 -177,7T, Дж;(2)

14 Fe₃O₄ + CO = 3/4 Fe_a + CO₂,

A r G T (14) = -18 844 - 9,66 T In T +

+ 86,695T, Дж;(14)

14Fe 3 O 4 + H 2 = 3/4Fe a + H 2 O,

A r G T (15) = 17 736 - 9,66 T In T +

+ 53,23T, Дж;(15)

C + CO₂ = 2CO,

ArGT (2) = 172 140 -177,7T, Дж.(2)

^x H 2

P - K 6 K 2 ( K 6 + 1) ,

P ( K 7 + 1)

^x H₂O =

- P - K 6 K 2 ( K 6 + 1)

⁷     P ( K 7 + 1)

.

Аналогично для определения параметров равновесия каждой из четырехкомпонентных четырехфазных систем:

Fe 3 O 4 -FeO-CO-CO 2 -H 2 -H 2 O-C при Т > 850 К;

FeO-Fe _a -CO-CO₂-H₂-H₂O-C при Т> 850 К;

Fe 3 O 4 -Fe _a -CO-CO 2 -H 2 -H 2 O-C при Т < 850 К следует решать систему четырех уравнений, рассчитывая равновесия трех независимых реакций:

Fe₃O 4 + CO = 3FeO + CO₂,

A _rG°_T (10) = - 10 034 - 38,635 T In T +

+271,78T, Дж;(10)

Fe₃O 4 + H₂ = 3FeO + H₂O,

A _r G T (11) = 26 546 - 38,635 T In T +

+238,315T, Дж;(11)

C + CO₂ = 2CO,

ArGT (2) = 172140-177,7T, Дж;(2)

Каждая из этих систем четырех уравнений, как и система (8), имеет единственное решение, определяемое уравнениями, аналогичными уравнениям (9). Результаты расчетов приведены в табл. 4–6 и на рис. 4 и 5. Эти рисунки согласуются с известным графиком, представляющим параметры устойчивости Fe3O4, FeO и Fe в газовой смеси СО–СО2 в присутствии углерода (рис. 3).

Пространственная диаграмма (рис. 4) определяет равновесные параметры устойчивости Fe 3 O 4 , FeO и Fe в атмосфере водяного газа в присутствии углерода. Заметим здесь, что криволинейная поверхность MGLFDCE , на которой лежат политер-мические линии AB , BC , BD и EF , соответствует поверхности MLFE на рис. 1. Для пояснения диаграммы проанализируем график, получающийся при проекции политермических линий AB , BC , BD и EF объемной диаграммы на плоскость x CO – x H 2 (рис. 5). Важнейшими параметрами, определяющими устойчивость Fe₃O₄, FeO и Fe, являются температура и концентрации в газовой фазе восстановителей x CO и x H 2 . Прямые линии 4–10 на рис. 5 представляют собой изотермы 850…1000 К (аналогичные таковым на рис. 2). Как было сказано в пояснениях к рис. 2, линии-изотермы соеди-

Таблица 4

Параметры равновесия в системе Fe 3 O 4 –FeO–ВГ–С при давлении 1 атм

Т , К	850	860	870	880	890	900	910	917
x CO	0,0545	0,0751	0,1029	0,1399	0,1892	0,2543	0,3395	0,4143
x CO2	0,0588	0,0842	0,1196	0,1689	0,2370	0,3308	0,4580	0,5731
x H 2	0,6613	0,6109	0,5498	0,4749	0,3826	0,2684	0,1265	0,0077
x H2O	0,2254	0,2298	0,2277	0,2163	0,1912	0,1471	0,0760	0,0049

Примечание. Выше - 917 К (644 °С) в уравнениях (9) второе слагаемое числителей становится больше единицы и решения не имеют физического смысла.

Таблица 5

Параметры равновесия в системе FeO-Fe _a -Br-C при давлении 1 атм

Т , К	850	870	890	910	920	930	940	950	955
x CO	0,0545	0,0891	0,1418	0,2217	0,2751	0,3399	0,4179	0,5118	0,5655
x CO2	0,0588	0,0889	0,1332	0,1951	0,2347	0,2812	0,3356	0,3991	0,4345
x H 2	0,6613	0,6050	0,5274	0,4192	0,3502	0,2691	0,1739	0,0625	- 5 - 10-5
x H2O	0,2254	0,2170	0,1976	0,1640	0,1400	0,1098	0,0726	0,0226	- 2 - 10-5

Примечание. Выше ~ 955 К в уравнениях (9) второе слагаемое числителей становится больше единицы и решения не имеют физического смысла.

Таблица 6

Параметры равновесия в системе Fe 3 O 4 -Fe _a -Br-C при давлении 1 атм

Т , К	850	830	800	750	700	650	600	550
x CO	0,0545	0,0315	0,0131	0,00261	4,17-Ю-4	5,0 - 10-5	4,32 - 10-6	2,4 - 10-7
x CO2	0,0588	0,0352	0,0152	0,00348	6,36 - 10-4	9,1 - 10-5	9,5 - 10-6	6,7 - 10-7
x H 2	0,6613	0,7048	0,7477	0,7901	0,8204	0,8480	0,8753	0,9019
x H2O	0,2254	0,2285	0,2240	0,2038	0,1786	0,1518	0,1247	0,0981

Примечание. При температурах ниже ~ 700 К концентрации СО и СО 2 исчезающее малы, а концентрация водорода велика.

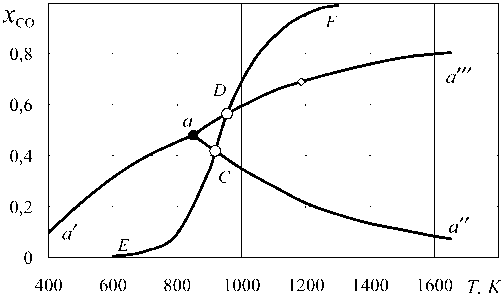
Рис. 3. Параметры равновесия в системе оксиды железа–СО–СО 2 –С: точка С – Т = 917 К, x _CO = 0,419, x _CO2 = 0,581; точка D – Т = 955 К, x _CO = 0,5654, x _CO2 = 0,4346

няют точку x CO = 0 и x H 2 = 1 с точками, координаты которых определяются параметрами равновесия реакции газификации углерода. Точки пересечения линий 3 и 4 (изотермы 917 и 955 К) на рис. 5 с осью x CO соответствуют координатам точки C ( x CO = 0,418 и x CO 2 = 0,582) и точки D ( x CO = 0,565 и x CO 2 = 0,435) и на рис. 3, и на рис. 4. Любые другие точки на изотермах определяют параметры устойчивости Fe _a , FeO + Fe _a , FeO, FeO + Fe₃O 4 , Fe 3 O 4 . Как видно (см. рис. 5), эти параметры зависят от температуры.

Это можно показать расчетами, например, для 910 К (табл. 7, линия 7 на рис. 5 и линия GJ на рис. 4). Эта изотерма соединяет точку G с координатами x CO = 0 и x H 2 = 1 и точку J с координатами x CO = 0,385, x CO 2 = 0,615, которая характеризуют равновесие реакции (2) при температуре 910 К. Точка пересечения n изотермы с линией 2 ( BC )

соответствует концентрациям x CO = 0,3395 и x _{H 2} = 0,1265 в водяном газе, равновесном со смесью FeO + Fe 3 O 4 и графитом (табл. 4). Точка пересечения h изотермы с линией 1 ( BD ) соответствует концентрациям x CO = 0,2217 и x H 2 = 0,4192 в водяном газе, равновесном с FeO + Fe _a и графитом (табл. 5). Любая точка на изотерме 910 К при x_CO <  0,2217 и x _H 2 >  0,4192 определяет параметры устойчивости Fe _a ; любая точка при 0,3395 >  x _CO >  0,2217 и 0,1265 <  x H 2 <  0,4192 - параметры устойчивости FeO; при 0,3395 < x _CO = 0,3 85 и 0,1265 >  x H 2 = 0 -устойчивость Fe 3 O 4 . Концентрации СО 2 и Н 2 О вычисляются по уравнениям:

xC2O xCO2 =      ; xH2O = 1 - (xCO + xCO2 + xH2 ).

K ₂

Таким образом, впервые представлена поли-термическая пространственная диаграмма фазовых

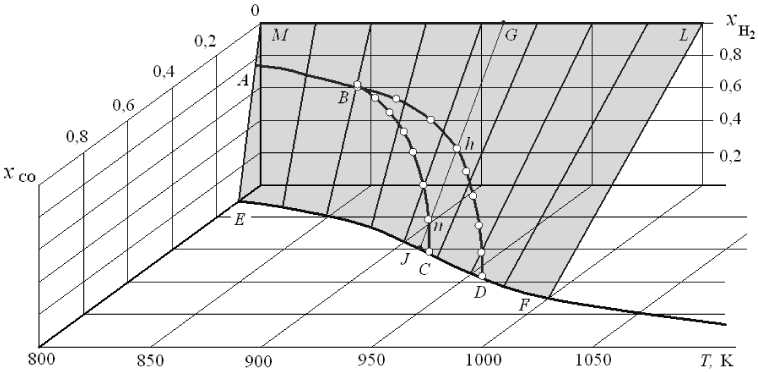
Рис. 4. Параметры равновесий в системах Fe 3 O 4 -FeO-Br-C (линия ВС ), FeO-Fe a -ВГ-С (линия BD ), Fe₃O₄-Fe _a -Br—C (линия АВ ) и СО-СО 2 -С (линия ECDF) при давлении 1 атм

Рис. 5. Концентрации Н 2 и СО в системах

Fe 3 O 4 -FeO-Br-C (линия 2, ВС ), FeO-Fe a -ВГ-С (линия 1, BD ) и Fe 3 O 4 -Fe a -Br-C (линия 3, AB ); изотермы: 4 – 850, 5 – 870, 6 – 900, 7 – 910, 8 – 920,

9 - 940; 10 - 1000, 11 - > 1300 К ( x CO + x H 2 = 1)

Таблица 7

Результаты расчета концентрации восстановителей СО и Н 2 в водяном газе, равновесном с графитом и оксидами железа при 910 К и общем давлении 1 атм

Концентрации Устойчивость Fe3O4 Fe3O4+ FeO (точка n) FeO FeO + Fe (точка h) Fe xCO > 0,3395 0,3395 0,3395–0,2217 0,2217 < 0,2217 xH2 > 0,1265 0,1265 0,1265–0,4192 0,4192 > 0,4192 равновесий при восстановлении оксидов железа водяным газом в присутствии углерода (см. рис. 4). Поверхность АBCJE на этой диаграмме определяет параметры устойчивости Fe3O4; поверхность BDC определяет параметры устойчивости FeO; поверхность MGLFDBA – параметры устойчивости железа. Для определения этих параметров можно воспользоваться проекцией линий поверхности на плоскость xCO – xH2 (см. рис. 5). На этом рисунке в области ABCF заданы температуры и концентрации компонентов водяного газа, при которых в присутствии углерода устойчива оксидная фаза Fe3O4. В области BCD заданы параметры устойчи- вости FeO, а в области выше и левее линии ABD – параметры устойчивости a-Fe, y-Fe и жидкого железа. Следует отметить, что металл насыщен углеродом (активность углерода по Раулю равна единице), а граница между ферритом и аустенитом, насыщенными углеродом, определяется изотермой 1011 К.

На метастабильной диаграмме фазовых равновесий при восстановлении оксидов железа в атмосфере водяного газа в отсутствии углерода, как это было показано в работах [1, 2], области устойчивости Fe3O4, FeO и железа объемные и границы между областями представляют собой поверхности. В присутствии углерода в качестве самостоятельной фазы пространственные области вырож- даются в поверхность, а границы между ними – в линии.

Следует отметить такую закономерность – устойчивость Fe α , FeO, Fe 3 O 4 в водяном газе в контакте с твердым углеродом возрастает с повышением концентрации водорода при одновременном понижении концентрации монооксида, но при повышении суммарной концентрации этих газов.

Для количественной оценки восстановительных способностей СО и Н 2 , присутствующих в газовой фазе, по рекомендациям автора монографии [3] следует сравнивать количества кислорода, отобранного у оксидов этими восстановителями. Для этого, кроме приведенной в настоящей работе информации, необходимо задавать количественное соотношение восстановителей в исходной газовой смеси СО–Н 2 , так как соотношение восстановительных способностей зависит не только от температуры.

Заключение

• 1.    Впервые построены пространственная диаграмма фазовых равновесий, реализующихся при восстановлении оксидов железа в атмосфере водяного газа в присутствии углерода, и их проекции.

• 2.    Рассчитаны координаты политермических поверхностей, на которых заданы составы водяного газа, равновесного со смесями твердых фаз: Fe 3 O 4 –С, Fe 3 O 4 –Fe(С)–С, Fe 3 O 4 –FeO–С, FeO–С, FeO–Fe(С)–С и Fe(С)–С.

• 3.    Разработанные методики могут быть использованы при анализах фазовых равновесий водяного газа с оксидами других металлов в отсутствии и присутствии углерода.