Системы леонтьевского типа и прикладные задачи
Бесплатный доступ
В статье представлен комплекс основных результатов, полученных в последние годы в аналитических и численных исследованиях различных задач для систем леонтьевского типа - конечномерного аналога уравнений соболевского типа. Ключевым фактором в достижении определенных успехов стало наличие прикладных задач, изучение каждой из которых представляло самостоятельный интерес. В статье будут представлены три математические модели, в основе которых лежит система леонтьевского типа: вырожденная балансовая динамическая модель производственного предприятия, вырожденная балансовая модель клеточного цикла, математическая модель сложного измерительного устройства. В рамках класса задач будут рассмотрены начальная задача Шоуолтера - Сидорова для системы леонтьевского типа и ряд задач оптимального управления для нее. Кратко будут изложены численные методы решения таких задач, показаны результаты о сходимости приближенных решений к точному. Особое внимание будет уделено задаче восстановления динамически искаженного входного сигнала по наблюдаемому выходному при наличии помех. Математическая модель сложного измерительного устройства построена как система леонтьевского типа, начальное состояние которой отражает условие Шоуолтера - Сидорова. Основным положением теории оптимальных динамических измерений является моделирование искомого входящего сигнала как решения задачи оптимального управления с минимизацией функционала штрафа, в котором оценивается расхождение моделируемого и наблюдаемого выходного (или наблюдаемого) сигналов. Наличие помех на выходе измерительного устройства приводит к необходимости использования в численных алгоритмах цифровых фильтров. Статья носит обзорный характер и дает целостное понимание направлений развития исследований систем леонтьевского типа.
Система леонтьевского типа, оптимальное управление, условие шоуолтера - сидорова, алгоритмы численного решения, оптимальное динамическое измерение, вырожденная балансовая динамическая модель предприятия
Короткий адрес: https://sciup.org/147237427
IDR: 147237427 | УДК: 517.9
Текст научной статьи Системы леонтьевского типа и прикладные задачи
Пусть L и M - квадратные матрицы порядка n , det L = 0 . Система леонтьевского типа
LX = Mx + у, (1)
является частным (конечномерным) случаем уравнения соболевского типа. Важным условием является (L,p) -регулярность матрицы M (существует а Е C такое, что det(aL — M ) =0 , p Е { 0 } U N - порядок полюса в точке то матриц-функции (aL — M ) - 1 ), вектор-функция у : [0; т ] Ч R n , т Е R + .
Системы вида (1) при условии det L = 0 не имеют единого, принятого всеми, названия, так в [1] их называют алгебро-дифференциальными, в [6] – дифференциально-алгебраическими, в [29] – вырожденными системами обыкновенных дифференциальных уравнений, в [17] – дескрипторными системами. Следует отметить, что все эти названия используются и тогда, когда L = L(t), M = M(t). Более точное название систем вида (1) приводило к громоздким формулировкам, и в [32] их было предложено называть системами леонтьевского типа, имея в виду их прототип – знаменитую балансовую модель В. Леонтьева с учетом запасов [18]. Безусловно, аналогичные системы позже возникли и в других прикладных задачах, но так как впервые системы вида (1) неразрешенные относительно производной в прикладном аспекте исследовал В. Леонтьев, отдавая дань соотечественнику, в научной школе профессора Г.А. Сви-ридюка, стали следовать названию – системы леонтьевского типа, считая, что оно и все приведенные выше являются синонимами.
В работах Г.А. Свиридюка и С.В. Брычева основные результаты теории относительно p -ограниченных операторов и вырожденных аналитических групп операторов были адаптированы к конечномерной ситуации [32]. Был построен численный алгоритм решения задачи Коши
x(0) = x o (2)
для системы вида (1) в случае, когда свободный член y – постоянный вектор. В качестве примера была построена динамическая балансовая модель городского жилищно– коммунального хозяйства. Численное решение задачи оптимального управления для системы леонтьевского типа с начальным условием Коши впервые исследовано в работах Г.А. Свиридюка и И.В. Бурлачко [2]. В обоих исследованиях численное решение задачи требовало проверки принадлежности начальных условий фазовому пространству, что существенно ограничило размер матриц, входящих в состав системы.
Использование в качестве начального условия Шоуолтера – Сидорова
[ (aL - M ) -1 Ly +1 (x(0) - x o )=0 (3)
позволяет купировать эту проблему, здесь a Е p L (M ) , p L (M ) — L -резольвентное множество оператора M . Более того, именно исследование задачи (1),(3) привело к развитию в научной школе профессора Г.А. Свиридюка аналитических и численных методов решения разных начальных, начально–краевых задач для различных уравнений соболевского типа [30, 35]. Здесь отметим развивающееся под руководством С.А. Загребиной направление по исследованию начально–конечных и мультиточеч-ных задач [34].
Особое значение в решении прикладных задач имеют результаты по исследованию задач оптимального управления. Впервые для уравнения соболевского типа задача оптимального управления была поставлена Г.А. Свиридюком и А.А. Ефремовым [31], в этой же работе были получены условия существования и единственности ее решения. Затем задачи оптимального управления начали активно исследоваться во всех направлениях челябинской научной школы профессора Г.А. Свиридюка по уравнениям соболевского типа: Н.А. Манаковой и ее учениками для полулинейных уравнений [19], А.А. Замышляевой и ее учениками для уравнений высокого порядка [36], А.В. Келлер для систем леонтьевского типа [7], М.А. Сагадеевой для неавтономных уравнений [21].
В период, когда был разработан численный алгоритм решения задачи оптимального управления для систем леонтьевского типа [10, 13], профессорами А.Л. Шестаковым и Г.А. Свиридюком был предложен новый подход к решению одной из основных задач оптимального измерения – восстановлению динамически искаженного входного сигнала по известному выходному сигналу [22]. Измерительное устройство в общем случае моделируется системой леонтьевского типа [16], а для восстановления сигнала используются методы оптимального управления, поэтому эта задача получила название задачи оптимального динамического измерения. Искажение сигнала обусловлено как инерционностью измерительного устройства, так и помехами различной природы – резонансами и шумом. Для решения задачи оптимального динамического измерения при наличии случайных помех исследования стали вестись по двум направлениям: развитие теории стохастических уравнений соболевского типа [3, 4, 23] и развитие численных методов [24, 26]. Необходимо подчеркнуть, что исследования стохастических уравнений в бесконечных гильбертовых пространствах ведутся в научной школе профессора И.В. Мельниковой [20], стохастических уравнений леонтьевского типа в терминах текущих скоростей – в научной школе профессора Ю.Е. Гликлиха [5].
В данной обзорной статье приводятся математические модели, в основе которых лежат системы леонтьевского типа, и ключевые результаты в развитии численных методов решения задач оптимального управления, полученные в научной школе профессора Г.А. Свиридюка, за исключением обобщенной математической модели измерительного устройства. Эта модель построена Ю.В. Худяковым [16], учеником А.Л. Шестакова, в рамках совместных научных исследований этих двух школ.
1. Математические модели леонтьевского типа
Динамическая балансовая модель предприятия
Межотраслевой баланс (МОБ) или межотраслевой анализ – это метод систематической установки взаимосвязей между различными секторами сложной экономической системы. Сама модель МОБ, описывающая экономику, практически может иметь как очень высокую размерность, так и малую. Она может представлять, формально никак не изменяясь, как экономику страны, так и отдельное предприятие [18]. Межотраслевой баланс представляет собой экономико-математическую модель процесса воспроизводства обычно в рамках годового цикла. Рассмотрим динамическую балансовую модель
x(t) = Ax(t) + Bx(t) + g(t). (4)
Здесь элемент a ij матрицы прямых затрат A означает количество продукции i -й отрасли необходимой для производства единицы продукции и/или услуги j -й отрасли, i,j = 1, 2,... ,n . В отличие от коэффициентов статической балансовой модели коэффициенты в динамической модели включают также затраты на возмещение выбытия и капитальный ремонт основных производственных фондов
Элемент bij матрицы B представляет определенный технологический запас особого типа благ – машин, механических инструментов, промышленных зданий и сооружений, рабочих запасов первичных и промежуточных материалов, производимой отраслью i, который используется отраслью j для производства единицы продукции и/или услуги им выпускаемым, или удельные капитальные вложения i,j = 1, 2,...,n. В любой динамической балансовой модели предприятия, матрица B всегда содержит нулевые строки, а условие det B = 0 является естественным в экономических приложениях, так как не все отрасли являются производительными. Элементы gi(t) вектор-функции g(t~) показывают выпуск конечного продукта i-й отраслью или спрос на продукцию i-й отрасли. Элементы xi (t) вектор-функции x(t) есть значения валово- го выпуска продукции i-й отрасли. По сути система (4) означает, что общая стоимость валового выпуска продуции распределяется на внутреннее потребление отраслей Ax, развитие основных производственных фондов Bx˙ и на внешнее потребление g(t).
Очевидно, что система (4) редуцируется к системе леонтьевского типа (1), где матрица M = I - A , L = B , y(t) = - g(t) с соответствующим экономическим смыслом.
Так в примере Леонтьева [18] рассматривались взаимосвязи между тремя отраслями экономики – сельским хозяйством, промышленностью и домашними хозяйствами. Матрицы L и M имеют вид:
|
/ 7 1 21 \ |
/ 3 - 1 - 11 \ |
||
|
20 20 20 |
4 5 20 |
||
|
L= |
1 103 8 |
, M= |
- 7 22 - 3 |
|
100 200 25 |
25 35 5 |
||
|
- 4 - 2 13 |
|||
|
000 |
15 15 15 |
||
Третья строка матрицы L является нулевой, так как труд невозможно запасти.
При возникшей практической значимости работ с балансовыми динамическими моделями в 50 – 80-е годы прошлого века, их методы построения и анализа создавались таким образом, чтобы избежать получения вырожденного случая или получения такого вида системы, чтобы была возможность ее исследования известным на то время математическим аппаратом. Многие исследователи отмечали, что система (4) может не иметь допустимых решений, удовлетворяющих некоторым начальным условиям. Для преодоления этого, например, предлагалась замена системы уравнений системой неравенств вида
x(t) ≥ Ax(t) + Bx˙ (t) + g(t).
Для составления балансовой модели для предприятия в [8] было предложено выделить виды деятельности по отношению к производимому продукту. С одной стороны, на предприятии специально не вычленяются все осуществляемые виды деятельности, особенно если они относятся к внутренним услугам. С другой стороны, любое предприятие имеет утвержденную организационную структуру, которая обычно относится к линейно-функциональной, и в рамках которой фактически выделены уже как различные отделы (или службы), так и виды деятельности. Кроме того, учет прямых затрат и учет основных средств имеет разделение в управленческом (или бухгалтерском) учете в соответствие с организационной структурой. Обычно первичный список подразделений гораздо шире необходимого для создания балансовой модели. Целесообразно сгруппировать подразделения по виду проводимых работ в создаваемый нами перечень видов деятельности с соответствующим суммированием показателей затрат и основных средств. Варьирование в модели любого конечного количества видов деятельности, и на основе производимого при этом агрегирования и дезагрегирования их объемов производства и потребления, влияющих на оценки производственных и экономических связей, позволяет приблизиться к оптимальной в балансе структуре.
Предлагается использовать три группы структурных элементов матриц, входящих в состав модели:
-
1) производительные виды деятельности, их продукт является конечным, к ним относят подразделения, выпускающие продукты (товары или услуги) и приносящие предприятию прибыль; обозначим их количество числом l ;
-
2) обслуживающие виды деятельности, их продукт является промежуточным, к ним относят подразделения компании, осуществляющие вспомогательную функцию, например, отдел логистики, маркетинга, сбыта, бухгалтерия и т.д.; обозначим их количество числом m ;
-
3) потребители конечного продукта или внешние виды деятельности, это структурный элемент модели, в который всегда входят две составляющие: домашнее хозяйство (в виде труда персонала компании) и корпоративные потребители (поставщики, контрагенты); обозначим их количество числом k .
Заметим, что l + m + k = n - порядку матриц, входящих в состав балансовой модели
В [8] была приведена балансовая модель реального предприятия при n = 24 и основные шаги работы. Для построения и расчета элементов матриц, входящих в балансовую модель, необходимо собрать первичную информацию: затраты по подразделениям и характеристики основных средств (балансовая и остаточная стоимость, амортизация за период), используемые в подразделениях. Выборку показателей затрат необходимо проводить с производственных счетов бухгалтерского учета по факту разнесения затрат по подразделениям до применения каких-либо калькуляций себестоимостей продукции/видов деятельностей. Для получения показателей учета основных средств также используются счета бухгалтерского учета.
Работа по формированию матриц для предприятия проводилась ≪ вручную ≫ и заняла больше года. Именно это послужило основой для разработки такой методики построения балансовой модели, которая бы позволила на структуре бухгалтерской отчетности, проводимой в программных продуктах, рассчитывать элементы матриц M и L . Эти работы проводились совместно с Виноградовой Т.А. [11].
Модель сложного измерительного устройства
В [16] представлена обобщенная математическая модель сложных измерительных устройств. Она включает в себя измерительные преобразователи, моделируемые подсистемами
Z i (t) = A i Z i (t) + B i u M i (t),
Умi(t) = C^t) + Di y (t), где zi (t), uMi (t), yMi (t) - состояние i-го измерительного преобразователя, состояние входов и выходов соответственно i-й подсистемы, а yi (t) - помехи (например, резонансы), наблюдаемые на выходе i-й измерительного преобразователя i = 1,2,..., N.
Отметим, что моделирование датчика системой такого вида (при N =1 ) было предложено А.Л. Шестаковым в 1987 году.
Введя обозначения
У М 1 ( t ) y M 2 (t)
S „ N (t)
y M (t) =
У м 1 ( t ) y M 2 (t)
У м N (t)
A = diag(A i , A 2 ,..., A n ), B = diag(B i , B 2 ,..., B n ),
C = diag(C i , C 2 , ..., C n ), D = diag( D 1 , D 2 ,..., D n ), модель комплекса N измерительных преобразователей представим системой
z(t) = Az(t) + BU m (t), u (t) = Cz(t) + D U t).
В сложных измерительных устройствах предполагается наличие линейных связей, которые задаются следующим образом f Um (t) = SllyM (t) + S12um (t) + S13uM (t) + S14yM (t)
[Ум (t) = S2^m (t) + S22UM (t) + S23UM (t) + S24yM (t), где yM (t) — моделируемое наблюдение; Sij - это матрицы соответствующих линейных связей, а uM (t) - моделируемый измеряемый сигнал, искажаемый помехами.
После некоторых преобразований и обозначения
x(t) = col(z(t),uM(t),yM(t),yM(t)), y(t) = Ум(t), системы (6) и (7) могут быть записаны в виде
(Lx(t) = Ax(t) + Bu M (t), [ y(t) = Cx ( t ) + Dn(t),
где
^U
^U
L=
|
I |
0 |
0 |
0 |
A |
B |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
, A = |
C |
D |
- I |
0 |
|
0 |
0 |
0 |
0 |
0 |
S 11 - I |
S 12 |
S 13 |
|
|
0 |
0 |
0 |
0 |
0 |
S 21 |
S 21 |
S 23 - |
I
B 1
B 2
S 14
S 24
b =
C = [ 0 0 0 I] .
В качестве примера приведем модель сложного измерительного устройства с итера- ционным принципом для восстановления динамически искаженного сигнала
U M 1 U M 1 ,
Z 1 = A 1 Z 1 + B 1 U M 1 , y M 1 = C 1 Z 1 + D 1 U 1 , U m 2 = U M 1 - У м 1 , Z 2 = A 2 Z 2 + B 2 U M 2 , < y M 2 = C 2 Z 2 + D 2 U 2 ,
U M 3 = U M 1 - y M 2 ,
Z N = A N Z N + B N y M N , y M n = C n z n + D n U n ,
< y M = y M 1 + y M 2 + ... + y M N + U M 1 — y M 1 — y M 2 — ... — y M N •
Система (9) отражает идею коррекции динамической погрешности при итерационном принципе, который состоит в последовательном использовании произвольного числа измерительных преобразователей, выход системы представляет собой сумму наблюдаемого сигнала и моделируемых итерационными звеньями погрешностей. Математическая модель такого измерительного устройства записывается в виде матричного уравнения для случая N = 2
η 1
\ ъ /
Таким образом, обобщенная математическая модель измерительного устройства представима в виде системы леонтьевского типа (8).
Динамическая балансовая модель клеточного цикла
Вырожденная динамическая балансовая модель клеточного цикла была предложена С.И. Эбель и была построена с использованием методики для динамической балансовой модели предприятия [9]. В рамках вырожденной динамической балансовой модели клеточного цикла модели (4) рассмотрим потоки вещества, энергии, информации для построения элементов матриц с выделением трех групп структурных элементов, соответствующих потокам вещества, энергии, информации.
К внутриклеточному потоку веществ относят реакции дыхательного обмена, которые поставляют энергию и снабжают клетку строительным белком для синтеза разнообразных молекул.
К внутриклеточному потоку энергии относят анаболические реакции (синтеза крупных молекул из более мелких и простых с затратами энергии) и катаболические реакции (распада крупных молекул на более мелкие и простые с выделением энергии). Совокупность катаболических и анаболических реакций, протекающих в клетке в любой данный момент, составляют ее метаболизм.
К внутриклеточному потоку информации относятся те, благодаря которым клетка приобретает структуру, отвечающую критериям живого, поддерживает ее во времени, а так же передает в ряду поколений. В потоке информации участвует ядро, макромолекулы приносящие информацию (матричная РНК) в цитоплазму, цитоплазматический аппарат трансляции (транспортная РНК, рибосомы полиномы) и др.
Живая клетка на временном интервале [t o , t o + т ] воспроизводит новую клетку, где t 0 – момент начала клеточного цикла, τ – время создания новой клетки. Время t Е [t 0 ,t 0 + т ] определяет текущий момент времени процесса создания новой клетки. Предполагается, что в начальный момент времени t 0 клетка обладает вещественным потенциалом (запасом вещества) m o = m(t o ) , энергетическим потенциалом (запасом энергии) e o = e(t o ) и информационным потенциалом (информационным ресурсом) u 0 = u(t o ) . Вектор Bx 0 = Bx(t 0 ) = (m o ,e o ,u o ) определяет начальные запасы вещества, энергии, информации в клетке. Окончание создания новой клетки определяется наличием удвоенного запаса Bx(t 0 + т ) = 2Bx(t o ) = 2BX 0 . Вектор x(t) определяет объем производства вещества (x 1 (t)) , энергии (x 2 (t)) и информации (х з (t)) в момент времени t Е [t o , t o + т ] . A и B - квадратные матрицы размера ( n х n ). Матрица A содержит элементы, показывающие удельные затраты вещества, энергии и информации необходимых для поддержания функционирования клетки, или нормы затрат i -го ресурса на синтез единицы j -го ресурса. Элементы матрицы B определяют нормы приращения внутриклеточных потоков i -го ресурса на прирост единицы j -го ресурса.
Охарактеризуем вектор f (t) = (f m (t), f e (t), f u (t)) : каждая компонента f (t) состоит из трех слагаемых f i (t) = f i o (t) + f i 1 (t) — f i 2 (t) , где f i o (t) - удовлетворение потребностей клетки за счет произведенных ресурсов f i 1 (t) - удовлетворение потребностей клетки за счет ресурсов внешней среды, f i 2 (t~) - отток произведенных ресурсов клетки во внешнюю среду в момент времени t .
С учетом отмеченных обстоятельств в каждый момент времени выполняется балансовое соотношение (4). Приведем модельный пример построения балансовой динамической модели клеточного цикла.
В первой группе выделяются следующие структурные элементы: расщепление липидов, нуклеиновых кислот, белков жиров; синтез белков, жиров, углеводов и транспорт (ЭПР, комплекс Гольджи, рибосомы).
Во второй группе выделяются следующие структурные элементы: анаболизм и катаболизм.
В третьей выделяются следующие структурные элементы: регуляция всех видов клеточной активности (ядро); передача наследственной информации ДНК.
|
Система (4) редуцируется к системе леонтьевского типа (1), где матрицы M и L |
||
|
имеют вид |
||
|
/ 1 — 0,25 0 — 0,35 0 0 \ |
||
|
0 1 — 0 , 2 0 — 0 , 05 — 0 , 05 |
||
|
0 — 0 , 3 1 — 0 , 05 — 0 , 05 0 |
||
|
M = I — A = |
, ,, |
|
|
— 0 , 3 — 0 , 1 — 0 , 1 1 — 0 , 05 — 0 , 05 |
, |
|
|
0 — 0,1 — 0,1 — 0,1 0, 9 — 0,1 |
||
|
0 — 0 , 1 — 0 , 1 — 0 , 1 — 0 , 2 1 |
||
|
/ 0 0,30 0,2 0 0 \ |
||
|
0 0 0,4 0 0,1 0,1 |
||
|
0 0,4 0 0,05 0,05 0 |
||
|
L = B |
, ,, = . |
|
|
0 , 4 0 0 , 1 0 0 , 05 0 , 05 |
||
|
0 0,10,1 0,1 0,1 0,1 |
||
|
\ 000 0 0 0/ |
||
Также моделировалось и взаимодействие клетки с внешней средой на временном интервале (t o ,т ) , определяя вектор-функцию y(t)
2. Задача Шоуолтера – Сидорова
Результаты аналитического и численного исследования задачи Шоуолтера – Сидорова для систем и различных моделей леонтьевского типа представлялись во многих работах, например [7–9]. Приведем ключевые результаты решения задачи (1), (3) в компактной форме. Пусть L и M – квадратные матрицы порядка n , причем det L = 0 .
Решением системы (1) называется вектор-функция x Е C 1 ((0; T ); R n ) П C ([0; T ]; R n ) , удовлетворяющая уравнениям системы. Решение системы (1) называется решением задачи (1), (3), если оно вдобавок удовлетворяет уравнениям (4).
Теорема 1. Пусть матрица M (L,p)-регулярна, p Е No и det M = 0. Тогда для любого Хо Е R+ и у Е Ср+1((0,т); R+) ПСр([0,т]; R+) существует единственное решение задачи (1), (3) x(y,t), которое к тому же имеет вид
x(y,t) = , lim Xk(y,t), k^+ж
где xk (y,t) определяется формулой xk (y, t)
- ]Т(M - 1 (I - Q k )L) q M -1 (I - Q k )y ( q ) (t) + X k x o + q =0
t
I Rf Qk y (s)ds,
^MГ Lr
k(P +1) J
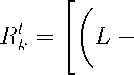
t
k(p + 1)
^ - 1 j k ( p +1) - 1
L
-
t
k(p + 1)
M
- 1
В условиях теоремы 1 для любого x 0 Е R + и y Е С р +1 ((0,т); R + ) П С р ([0,т]; R + ) . 3 K Е N такое, что при k > K существует единственное приближенное решение задачи (1), (3) X k (y,t) , которое определяется формулой
X k (y, t) = - J2 (M - 1 (I - Q k ) l' M - 1 (I - Q k ) y ( q ) (t)+ q =0
2 p
+ X k x o + ^ ^ R k j Q k y(t j^j , j =1
здесь для вычисления определенного интеграла используется квадратная формула
Гаусса, ^ j и S j - веса и узлы формулы, а t j = 2 + S>s^ '
3. Задачи оптимального управления
Для постановки задач оптимального и жесткого управления введем в рассмотрение пространство управлений
U = {u G L2 ((0, T); Rn) : u(p+1) G L2 ((0, т); Rn) , p G {0} U N} и пространство состояний
X = { x G L 2 ((0, т ); R n ) : x G L 2 ((0, т ); R n ) } .
В пространстве U выделим компактное выпуклое множество U ∂ – множество допустимых управлений .
Решение задачи оптимального управления для системы леонтьевского типа заключается в нахождении пары (v,x(v)) G U d x X почти всюду на (0,т) , удовлетворяющую системе
Lx = Mx + f + Bu, (10)
с начальным условием Шоуолтера – Сидорова (3), при этом
J (v) = min J (u), (11)
u ∈ U∂
1 r 2 ^
J(u) = в УУ / Cx^ (u,t) — Cx 0 q (t) dt + (1 — в ) У^
q =0
q =0
τ
/ N u < q > dt. (12)
Здесь ||-|| и (•) - норма и скалярное произведение в R n соответственно, C - квадратная матрица порядка n , N q - симметричные положительно определенные матрицы, q = 0,p +1 , д = 0,p +1 , в , 1 — в — весовые коэффициенты целей управления достижения плановых показателей и минимизации управляющего воздействия.
В качестве множества допустимых управлений принимается
£ /|««(t) | 2 dt < d. q =0 0
Если положить в = 1 , то получим задачу жесткого управления .
Для постановки задач стартового и стартового жесткого управления введем в рассмотрение пространство
Y = {y G L2 ((0, т); Rn) : y(p+1) G L2 ((0, т); Rn), p G {0} U N} и пространство состояний
X = { x G L 2 ((0, т ); R n ) : x G L 2 ((0, т ); R n ) } .
Пространство управлений U = R n . В пространстве U выделим замкнутое выпуклое множество U d - множество допустимых управлений
К < d.
Задача стартового управления. Найти пару (v o ,x(v o )) Е U d х X почти всюду на (0,т) , удовлетворяющую системе леонтьевского типа (1) с начальным условием Шоуолтера – Сидорова
[(^L - M)-1L]p+1 (x(0) - uo) = 0, при этом
J (v o ) = min J(u o ) u 0 ∈ U∂
τ
J(u o ) = в V / Cx ( q ) (У, u o , t) - Cx O q (t)
q =o
dt + (1 — в ) ||uo|| 2 •
Если положить в = 1 , то получим задачу стартового жесткого управления .
Здесь приведем результаты о виде точного и приближенного решения только задачи оптимального управления для систем леонтьевского типа (10) – (13), основные этапы алгоритма численного решения этой задачи. Для других задач основные этапы те же, отличия обусловлены видом начального условия и функционалом качества. Более подробное изложение в [8]. Справедлива следующая
Теорема 2. Пусть матрица M (L,p)-регулярна, p Е N o , т Е R + , причем det M = 0. Тогда для любых x o Е R n , f Е H p +1 (R n ) существует единственное решение (v,x(v)) Е U d х X задачи оптимального управления (10) - (13), где v - точка минимума функционала качества (12), а x(v) определяется формулой
x(v) = lim X k (v,t) = lim - V (M - 1 (I - Q k )L) q M - 1 (I - Q k )(f + Bv) ( q (t) + k > ■ ^ k > ■ ^ '
q =0
τ
+X k X o + ^ R k s Q k (f (s) + Bv(s))ds • 0
Здесь
Q k = (kL LL (M )) p +1 , Xk = ((L - tM) -1 L^ ,
R=((L - kM ) -1 L)" 1 (L - я 1
.
Для нахождения приближенного решения u(t) будем использовать представление ul(t) = col
£ a1j tj _£anj tj , j=0 j=0
где l Е N , учитывая вид первого слагаемого в формуле (14) I необходимо брать таким, чтобы ℓ > p .
Обозначим приближенное решение задачи оптимального управления (10) – (13) парой (v k ,x k ) .
Представление (15) u l (t) подставим в (14) и (12). Тогда функционал качества запишется следующим образом
1 т Jk = Е \ q=0 0
Cx^
2 6 Т
(u l ,t) - Cx 0 q ) (t) dt + E \ (N q (u l ) ( q ) (t), (u l ) ( q ) (t)) dt,
q =0
где X k (u l ,t) имеет вид
p
X k (ue, t) = - E ( M - 1 (I - Q k )L ) q M -1 (I - Q k )(f + BU) ( q ) (t) + q =0
t
+Xk X o + j R k s Q k ( f (s) + BU(s) ) ds.
Отметим, что v k - точка минимума этого функционала, т.е.
J(Vk. ) = min J k (u 1 ).
u ℓ ∈ U l ∂
Найдя v k и подставив вместо u l в X k (u l ,t) , получим X k. , т.е. X k, = X k (V k ,t) . Парой (v,x(v)) обозначается точное решение, а парой (V k ,X k. ) - приближенное решение задачи оптимального управления (10) – (13).
4. Алгоритм численного решения задачи оптимальногоуправления
Алгоритм нахождения приближенного решения задачи оптимального управления сводится к семи этапам [8].
Этап 1. Вычисление det M . Проверка на отличие его значение от нуля с точностью е . В случае det M = 0 необходимо провести замену z = extX и продолжить нахождение решения.
Этап 2. Вычисление порядка полюса p = n — q , где q = degdet(aL — M ) .
Этап 3. Вычисление числа K , начиная с которого можно вычислять приближенное решение K = max { k 1 , k 2 } . Здесь
q ki = -Еы + 1, V
V = max|l, | -1- | E l a i |j ,
q k2 = —pE l-i l(P + 1)П- + 1.
Этап 4. По заданному количеству узлов и отрезку интегрирования [0, т] осуществляется расчет весов ω j и узлов s j квадратурной формулы Гаусса.
Этап 5. В заданных точках d j Е [0,т] при нулевых значениях a ij из (15) вычисляются X k (0 , t ) и J k (0) .
Этап 6. Находится минимум функционала J(vk) и точка минимума vk = col
(Z a l t j , \ j =0
- t ai tj) . j =0 /
Нахождение неизвестных a i ∗ j сводится к реализации многошагового метода покоординатного спуска с памятью [13].
Этап 7. Вычисляется значение x ^ •
Обсуждая алгоритм, следует подчеркнуть, что при распараллеливания процессов алгоритм может быть улучшен: выбор изменяемых элементов в строках можно осуществлять при сопоставлении изменений не в одной строке, а во всех одновременно.
Сходимость приближенного решения к точному доказана в [33]. Справедлива следующая
Теорема 3. Пусть матрица M (L,p)-регулярна, p Е N0, det M = 0. Функционал (12) является непрерывной, сильно выпуклой функцией на компактном выпуклом множестве Ud С U. Пусть (v,x(v)) - точно, а (vlk,xlk) - приближенное решение задачи оптимального управления (10) - (13). Тогда последовательность {vlk} сходится к {v} по норме U, последовательность {xlk} сходится к x(v) по норме X при k Ч ж, l Ч ж, при этом Jk(vlk) Ч J(v), причем выполняется неравенство q ^vk - vH2 < Jk(vk) - J(v).
Отметим, что алгоритм был разработан первоначально для исследования вырожденной динамической балансовой модели и задач оптимального управления для нее. При решении прикладных инженерных задач, о которых речь пойдет далее, время работы алгоритма составляло несколько десятков часов. Именно этот недостаток привел к необходимости использования распараллеливания процессов и (или) сплайн-функций.
5. Задача оптимального динамического измерения
В теории оптимальных динамических измерений важной математической моделью является модель ИУ. Его динамические свойства определяются системой леон- тьевского типа
J LX = Ax + Bu + GZ, | y = Cx + Dn,
а его состояние в начале работы – начальным условием Шоуолтера – Сидорова
[(aL - A) - 1 L] p +1 (x(0) - x o ) = 0
при некоторых x 0 Е R n , a Е p L (A) . Математическая модель ИУ (16), (17) связывает x(t) и x(t) — вектор-функции состояния и скорости изменения состояния ИУ соответственно; y(t) - вектор-функция наблюдений (или выходного сигнала); A и L - квадратные матрицы состояний и взаимовлияния скоростей состояния ИУ соответственно; C и D - матрицы, характеризующие связи между состоянием ИУ и наблюдением; u(t) - вектор-функция измерения (или входного сигнала); n(t) и Z(t) — вектор-функции помех на выходе и в цепях ИУ соответственно.
В [22,25] для решения задачи восстановлении входного сигнала сигнала u = u(t) по наблюдаемому выходному сигналу y = y 0 (t) конструируется модель ИУ, при этом ee качество оценивается величиной расхождений значений выходных сигналов ИУ и его модели при соответствующих t . Поэтому в математической модели оптимальных динамических измерений, как задачи оптимального управления, необходимым условием для построения функционала штрафа является отражение в нем разности между выходными сигналами реального ИУ и его математической моделью. Минимизация функционала обеспечивает нахождение такого входного сигнала, который является математической моделью искомого измерения (см. рисунок).
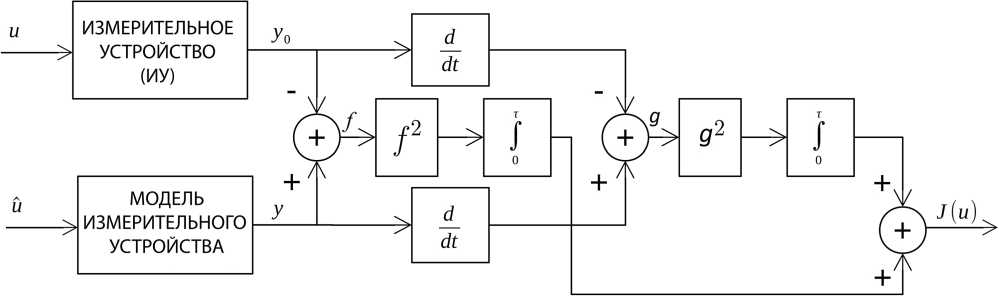
Структурная схема математической модели динамических измерений
Для построения математической модели оптимальных динамических измерений будем использовать пространство состояний X = { х 6 L 2 ((0, т), R n ) : x е L 2 ((0, т), R n ) } , пространство измерений U = { u е L 2 ((0,т), R n ) : u ( p +1) 6 L 2 ((0,т), R n ) } и пространство наблюдений Y = C [х] , причем Y изоморфно некоторому подпространству в х , хотя не всегда Y = х .
Функционал штрафа имеет вид
1 Т J (u) = Е / q=0 о
y ( q (u^) - y 0 q ) ( t )
dt,
где y 0 (t) - выходной сигнал, получаемый в ходе натурного эксперимента, y(t) - моделируемый выходной сигнал (получаемый при работе с математической моделью восстановления динамически искаженного сигнала), ||·|| – евклидова норма в R n .
Будем искать решение задачи на множестве допустимых моделируемых измерений U ∂ . В качестве U ∂ возьмем компактное выпуклое подмножество U:
U d = { u е U :
р +1 т
E / ^ u ( q ) (t) ^ 2
q =0 о
dt ≤ d } ,
где d = const .
Таким образом, задача оптимального динамического измерения заключается в нахождении такой вектор-функцию моделируемого измерения v ∈ U ∂ , при которой функционал штрафа (18) достигает минимального значения, т.е.
J(v) = min J(u), u∈U∂ при этом x(v) Е х удовлетворяет системе (16) почти всюду на (0,т) и при некоторых Хо Е Rn, а Е pL(M) — условию Шоуолтера - Сидорова (17).
Вектор-функцию v Е U d , начиная с первых работ по теории оптимальных динамических измерений, называют оптимальным динамическим измерением [22]. Представленную задачу (16) – (20) называют основной задачей оптимальных динамических измерений.
Подчеркнем, что требование близости не только значений наблюдаемого сигнала и моделируемого наблюдения, но и скоростей их изменения, обосновано результатами качественных исследований и присутствует во всех математических моделях оптимальных динамических измерений [14, 15, 26–28]. Однако, отметим, что при отсутствии помех искажение входного сигнала обусловлено только инерционностью измерительного устройства. Справедлива следующая
Теорема 4. Пусть L и A - квадратные матрицы порядка п, матрица A - (L; p)-регулярна, det A = 0. Тогда для любого х 0 Е R n существует единственное решение v Е А д задачи (16) - (20), при этом x (v) Е ^ удовлетворяет системе (16), условию (17) и определяется формулой
x(v) = lim x k (v,t) k ^ + ж
lim - V(A-1(I - Qk)L)qA-1 (I - Qk)(Bv)'q'(t) + k > + ^
L q =0
τ
+ X k x 0 +
I R^Qk(Bv(s))ds 0
Здесь
Qk = № (A)) p +1
Xt = (LL - ^ЛГ^ ,
R =0L - tA) -1 L)"1 (L - я
Заметим, что вид функционала штрафа обусловлен также и постановкой задачи, например, при наличии резонансов в цепях ИУ функционал штрафа имеет вид
J (u)
1 T в^ Sy ' “ 'A A
q =0
+ sy O q (t) - Sy 0 q ' (t)
dt+
θ τ
+(1 - в ) E / q =0 0
( F q U ( q ' (t),U ( q (t) ) dt,
где y0(t) = col(y01(t), y02(t),..., y0m(t)) - наблюдаемые сигналы, получаемые в ходе натурного эксперимента, y0 (t) - наблюдаемые сигналы, получаемые в ходе натурного эксперимента при отсутствии полезных измеряемых сигналов, y(t) - наблюдаемые сигналы, как результат математического моделирования процесса восстановления динамически искаженных сигналов, матрица S позволяет в функционале штрафа учитывать только ту часть наблюдений, которые используются для восстановления динамически искаженных сигналов при моделировании процесса (например, наблюдаются сигналы датчиков давления и температуры, а восстановление измеряемого сигнала проводится только по данным датчика давления). Коэффициенты в Е (0,1] и 1 — в - весовые, Fk - симметричные неотрицательно определенные матрицы порядка n, ||-|| и (-, •) - евклидовы норма и скалярное произведение в Rn [24].
В [24] представлены численные методы, позволяющие решать данную задачу: метод многошагового покоординатного спуска с памятью (этот алгоритм представлен в п. 4) и сплайн-метод.
Кратко изложим суть сплайн-метода решения задачи оптимальных динамических измерений.
Пусть заданы: матрицы, входящие в состав системы (1): начальное значение x o Е Rn ; массив наблюдаемых значений Y o i в узловых точках t i , i = 0,1,...,n выходящего сигнала, причем ti + 1 — t i = 5 , t 0 = 0 , t n = т .
Отрезок [0,т] разбивается на M отрезков [т т- 1 ,т т ] , где m = 1, 2,...,M , причем t 0 т 0 0 , t n т М .
На каждом отрезке [т т- 1 ,т т] строится интерполяционная функция y 0 m (t) в виде многочлена степени I < nM .
Последовательно для m = 1, 2, ...,M на [тт-1 ,Tm] решается задача оптимального динамического измерения (16) - (20) при и Е Udm , где и Е Udm С Ud — замкнутое выпуклое подмножество и Е Ud. Приближенное значение оптимального измерения vkm (t) находится в виде многочлена степени I, налагая условие непрерывности vkm(Tm) = vk,m+1(Tm). (21)
В результате получаем непрерывную на [0,т] сплайн-функцию v k (t) = U v km (t) . В [15] показана сходимость приближенного решения, т.е. сплайн-функции v k (t) , к точному решению v(t) задачи (16) - (20) на [0,т] . Она следует из:
-
1) сходимости интерполяционного процесса при построении сплайн-функции y o ( t ) = Uy e om (t) , т.е. Il y o ( t ) — y o (t) № при M чю ;
-
2) сходимости приближенного решения v k (t) к точному v m (t) на отрезке [т т- 1 ,т т ] при m = 1, 2,..., M на основании теоремы 3;
-
3) непрерывности сплайн-функции v k (t) на [0,т] , получаемой при выполнении условия (21).
В течение последних лет для фильтрации шумов используется подход, при котором с помощью цифровых фильтров проводится сглаживание наблюдаемого сигнала с последующим применением сплайн–метода. В одной группе цифровых фильтров – фильтр скользящей средней [27], цифррой фильтр Савицкого – Голлея [14] – на основе вычислительных экпериментов определялись параметры фильтра. В одномерном цифровом фильтре Калмана [24] используются статистические характеристики шума. Кроме того, эффективным оказался и новый сплайн–метод с простым усреднением [28]. Важным в этом методе является определение шага дискретизации с использованием теоремы Котельникова. Большое значение в развиитии численных методов имеет тот факт, что данными для вычислительных экспериментов являются результаты испытании датчика давления Метран-43 с аналоговым электронным преобразователем на стенде лаборатории Южно–Уральского государственного университета.
Эта статья написана в знак глубочайшего почтения и искренней благодарности своему научному руководителю и консультанту профессору Георгию Анатольевичу Свиридюку за поддержку и ценные советы на протяжении всей исследовательской деятельности автора.
Работа проводилась при финансовой поддержке Министерства науки и высшего образования Российской Федерации, грант FENU-2020-0022 (2020072ГЗ).
Список литературы Системы леонтьевского типа и прикладные задачи
- Boyarintsev Yu.E., Chistyakov V.F. Algebro-differencial’nye sistemy: metody resheniya i issledovaniya [Algebrodifferential Systems: Methods of Solution and Research]. Novosibirsk, Nauka, 1998. (in Russian)
- Burlachko I.V., Sviridyuk G.A. An Algorithm for Solving the Cauchy Problem for Degenerate Linear Systems of Ordinary Differential Equations. Computational Mathematics and Mathematical Physics, 2003, vol. 43, no. 11, pp. 1613–1619.
- Favini A., Sviridyuk G.A., Sagadeeva M.A. Linear Sobolev Type Equations with Relatively p-Radial Operators in Space of “Noises”. Mediterranean Journal of Mathematics, 2016, vol. 13, no. 6, pp. 4607–4621. DOI: 10.1007/s00009-016-0765-x
- Favini A., Sviridyuk G.A., Manakova N.A. Linear Sobolev Type Equations with Relatively p-Sectorial Operators in Space of “Noises”. Abstract and Applied Analysis, 2016, vol. 13, pp. 1–8. DOI: 10.1155/2015/697410
- Gliklikh Yu.E., Mashkov E.Yu. Stochastic Leontieff Type Equations in Terms of Current Velocities of the Solution II. Bulletin of the South Ural State University. Series: Mathematical Modelling, Programming and Computer Software, 2016, vol. 9, no. 3, pp. 31–40. DOI: 10.14529/mmp160303
- Hairer E., Lubich C., Roche M. The Numerical Solution of Differential–Algebraic Systems by Runge–Kutta Methods. Switzerland, Universite de Geneve, 1988.
- Кeller A.V. [Leontief Type Systems: Classes of Problems with Showalter–Sidorov Initial Condition and Numerical Solutions]. The Bulletin of Irkutsk State University. Series: Mathematics, 2010, vol. 3, no. 2, pp. 30–43. (in Russian)
- Keller A.V. Numerical Study of Optimal Control Problems for Leontief Type Models. PhD Thesis, Chelyabinsk, 2011. (in Russian)
- Keller A.V. The Algorithm for Solution of the Showalter–Sidorov Problem for Leontief Type Models. Bulletin of the South Ural State University. Series: Mathematical Modelling, Programming and Computer Software, 2011, no. 4 (221), pp. 40–46.
- Keller A.V. On the Algorithm for Solving Problems of Optimal and Rigid Control. Software and Systems, 2011, no. 3. pp. 38–42.
- Keller A.V., Shishkina T.A. The Method of Constructing Dynamic and Static Balance Models at the Enterprise Level. Bulletin of the South Ural State University. Series: Economics and Management, 2013, vol. 7, no. 3, pp. 6–10.
- Keller A.V., Ebel S.I. [On a Degenerate Discrete Balance Dynamic Model of the Cell Cycle]. South Ural Youth School of Mathematical Modelling, 2014, pp. 74–79. (in Russian)
- Keller A.V. On the Computational Efficiency of the Algorithm of the Numerical Solution of Optimal Control Problems for Models of Leontieff Type. Journal of Computational and Engineering Mathematics, 2015, vol. 2, no. 2, pp. 39–59.
- Keller A.V. Optimal Dynamic Measurement Method Using the Savitsky–Golay Digital Filter. Differential Equations and Control Processes, 2021, no. 1, pp. 1–15.
- Keller A.V., Sagadeeva M.A. Convergence of the Spline Method for Solving the Optimal Dynamic Measurement Problem. Journal of Physics, 2021, vol. 2021, article ID: 012074, 6 p. DOI: 10.1088/1742-6596/1864/1/012074
- Kondyukov A.O. Generalized Model of Incompressible Viscoelastic Fluid in the Earth’s Magnetic Field. Bulletin of the South Ural State University. Series: Mathematics. Mechanics. Physics, 2016, vol. 8, no. 3, pp. 13–21. DOI: 10.14529/mmph160302
- Kurdjukov А.P., Belov A.A. Deskriptornye sistemy i zadachi upravleniya [Descriptor Systems and Control Problem]. Moscow, Fizmatlit, 2015.
- Leont’ev V.V. Mezhotraslevaya ekonomika [Intersectoral Economics]. Moscow, Economics, 1997. (in Russian)
- Manakova N.A. Mathematical Models and Optimal Control of the Filtration and Deformation Processes. Bulletin of the South Ural State University. Series: Mathematical Modelling, Programming and Computer Software, 2015, vol. 8, no. 3, pp. 5–24. DOI: 10.14529/mmp150301
- Melnikova I.V., Alshanskiy M.A. Stochastic Equations with an Unbounded Operator Coefficient and Multiplicative Noise. Siberian Mathematical Journal, 2017, vol. 58, no. 6, pp. 1052–1066. DOI: 10.1134/S0037446617060143
- Sagadeeva M.A., Zagrebina S.A., Manakova N.A. Optimal Control of Solutions of a Multipoint Initial-Final Problem for Non-Autonomous Evolutionary Sobolev Type Equation. Evolution Equations and Control Theory, 2019, vol. 8, no. 3, pp. 473–488. DOI: 10.3934/eect.2019023
- Shestakov A.L., Sviridyuk G.A. A New Approach to Measurement of Dynamically Perturbed Signals. Bulletin of the South Ural State University. Series: Mathematical Modelling, Programming and Computer Software, 2010, no. 16 (192), pp. 116–120.
- Shestakov A.L., Sviridyuk G.A., Khudyakov Yu.V. Dynamic Measurements in “Noise” Spaces. Bulletin of the South Ural State University. Series: Computer Technologies. Control. Electronics, 2013, vol. 13, no. 2, pp. 4–11.
- Shestakov A.L., Sviridyuk G.A., Keller A.V., Zamyshlyaeva A.A., Khudyakov Yu.V. Numerical Investigation of Optimal Dynamic Measurements. Acta IMEKO, 2018, vol. 7, no. 2, pp. 65–72. DOI: 10.21014/acta_imeko.v7i2.529
- Shestakov A.L., Keller A.V., Zamyshlyaeva A.A., Manakova N.A., Zagrebina S.A., Sviridyuk G.A. The Optimal Measurements Theory as a New Paradigm in the Metrology. Journal of Computational and Engineering Mathematics, 2020, vol. 7, no. 1, pp. 3–23. DOI: 10.14529/jcem200101
- Shestakov A.L., Zagrebina S.A., Manakova N.A., Sagadeeva M.A., Sviridyuk G.A. Numerical Optimal Measurement Algorithm under Distortions Caused by Inertia, Resonances, and Sensor Degradation. Automation and Remote Control, 2021, vol. 82, no. 1, pp. 41–50. DOI: 10.1134/S0005117921010021
- Shestakov A.L., Keller A.V. Optimal Dynamic Measurement Method Using Digital Moving Average Filter. Journal of Physics, 2021, vol. 2021, article ID: 012073, 7 p. DOI: 10.1088/1742-6596/1864/1/012073
- Shestakov A.L., Zamyshlyaeva A.A., Manakova N.A., Sviridyuk G.A., Keller A.V. Reconstruction of a Dynamically Distorted Signal Based on the Theory of Optimal Dynamic Measurements. Automation and Remote Control, 2021, vol. 82, no. 12, pp. 2143–2154. DOI: 10.1134/S0005117921120067
- Skripnik V.P. Degenerate Linear Systems. Russian Mathematics, 1982, no. 3, pp. 62–67.
- Sukacheva T.G., Matveeva O.P. The Problem of the Thermoconvection of an Incompressible Viscoelastic Kelvin–Voigt Fluid of Nonzero Order. Russian Mathematics, 2001, vol. 45, no. 11, pp. 44–51.
- Sviridyuk G.A., Efremov A.A. Optimal Control for a Class of Degenerate Linear Equations. Doklady Akademii Nauk, 1999, vol. 364, no. 3, pp. 323–325.
- Sviridyuk G.A., Brychev S.V. Numerical Solution of Systems of Equations of Leontief Type. Russian Mathematics, 2003, vol. 47, no. 8, pp. 44–50.
- Sviridyuk G.A., Keller A.V. On the the Numerical Solution Convergence of Optimal Control Problems for Leontief Type System. Journal of Samara State Technical University. Series: Physical and Mathematical Sciences, 2011, no. 2 (23), pp. 24–33. (in Russian)
- Zagrebina S.A., Konkina A.S. The Multipoint Initial-Final Value Condition for the Navier–Stokes Linear Model. Bulletin of the South Ural State University. Series: Mathematical Modelling, Programming and Computer Software, 2015, vol. 8, no. 1, pp. 132–136. DOI: 10.14529/mmp150111
- Zamyshlyaeva A.A., Muravyev A.S. Computational Experiment for One Mathematical Model of Ion-Acoustic Waves. Bulletin of the South Ural State University. Series: Mathematical Modelling, Programming and Computer Software, 2015, vol. 8, no. 2, pp. 127–132. DOI: 10.14529/mmp150211
- Zamyshlyaeva A.A., Manakova N.A., Tsyplenkova O.N. Optimal Control in Linear Sobolev Type Mathematical Models. Bulletin of the South Ural State University. Series: Mathematical Modelling, Programming and Computer Software, 2020, vol. 13, no. 1, pp. 5–27. DOI: 10.14529/mmp200101


