Скалярное и векторное дифференцирование векторов

DOI:

Работа посвящена рассмотрению операций дифференцирования на пространстве векторных полей и гладких функций в R ³.

В механике достаточно широко используется производная скалярной функции по вектору [2; 3; 6]. В какой-то мере подобно ей определяется производная вектора по другому вектору [1]

d a d b

да,    да, да,

=    b x +    b y +    b z .

д x     д y ^y   д z

Вместе с тем формально интерпретируя производную как отношение дифференциалов, можно ввести в рассмотрение скалярную и векторную производные вектора по другому вектору, которые могут иметь приложение к решению задач механики.

Деление векторов

Определение 1. Частное a/b от деления скаляра a на вектор b есть вектор a a b   ab   a c = — =---=---= —7b .

b b b b • b b ²

Обратно,

a b • c = b • —b = a.

b ²

В частности,

1 = A b = b ^{2 .}

Определение 2. Частное e / b от скалярного деления вектора e на вектор b есть скаляр

e 1 b e • b c e p = — = e • — = e • —7 = —T- = —7 =—cos6, b b b2 b2 b2 b ,

где q – угол между векторами e и b . При этом

eb

--= cos 0

be

.

Определение 3. Частное e + b от векторного деления вектора e на вектор b есть вектор

q = e - b = e x —= e b

b e x b d e d .

x—- = —— = —- =-- sin 6 .

b ²     b ²     b ² b d

При этом

b

e

( e ^- b ) • ( b ^{- e} ) = ^- sin 6 , be

^- ( e ^- b ) • ( b ^- e ) = ¹, p + q = — . b ²

Теорема 1. Если известны частные от скалярного p и векторного q деления двух векторов e и b , а также делитель b , то делимое определяется как

e = b p + b x q .

Доказательство.

b p + b x q = ^2 [ b ( e • b ) + b x ( e x b ) ] = p- [ b ( e • b ) + e ( b • b ) - b ( b • e ) ] = e .

Теорема доказана.

Теорема 2. Если известны частные от скалярного p и векторного q деления двух векторов e и b , а также делимое e , то делитель определяется как

p e + q x e b =—2---■ p + q

.

Доказательство.

p e + q x e _ 1 p² + q² b²

b2

—[( e • b ) e + ( e x b ) x e

' ] = - 2 [ ( e • b ) e + b ( e • e ) - e ( e • b ) ] = b .

Теорема доказана.

Скалярная производная вектора по другому вектору

Определение 4. Операция

1 da db называется скалярной производной векторного поля a = axi + ayj + azk по векторному полю b = bxi + byj + bzk.

Теорема 3. Имеет место формула

1    da   da   da

da--= —- + —- + —- db db   db   db .

xyz

Доказательство.

d a • — = d ( a i + a j + a k ) • d b        x y z

d ( b x i + b y ^j + b z ^k )

= ( da_x i + da y j + da z k ) •

db i + db , j + db k xyz

= da_x i •

db i

—— + da, j • dbi + db„j + db,k dbi    y xyzx

db y j

•--+

db i + db,, j + db, k db,, j xyzy

+ da z k •

db_z k

--- dbx i + dby j + dbz k dbz k

= da_x i •

db_x i

( db_x i + db_y j + db z k ) • db_x i

db j

+ da „j--y-----------+ y (dbx i + dby j + dbz k) • dby j

+ da z k •

db_z k

(dbx i + dby j + dbz k) • dbz k daxi • dbxi + da-j • db-j dazk • dbzk

db x ²

db y ²

+

db_z ²

da db

—x—- + dbx2

da_ydb_y db y ²

da db zz dbz2

da   d^a   da

= —- +  - + —z- db   db   db .

xyz

Теорема доказана.

случай, когда берется скалярная производная по радиус-

Представляет интерес частный вектору r = x i + y j + z k .

,   1    d a_x    6 a y   d a

.

da--= —- + —- + —- = diva = V • a dr   dx   dy   dz

Следствие. Имеет место формализм:

d • — = V-

dr

Замечание. При решении ряда задач механики для упрощения вычислений систему координат выбирают таким образом, чтобы, по крайней мере, направление некоторых векторов совпадало с одной из координатных осей. Если это касается вектора, по которому предполагается выполнить дифференцирование, то в таких случаях формула (1) использоваться не может, поскольку некоторые дифференциалы этого вектора равны нулю.

Это обстоятельство обусловливает следующие две теоремы.

Теорема 4. Имеет место формула

1 da da

da--= —1 + —2, d (bxex + b 2e2) dbx db 2

где e – орты.

Доказательство.

da--= d (otjCj + a 2e2 + a 3e3)-- d (bxex + b 2e2)                             d (bxex + b 2e2)

db _x e _x + db ₂ e ₂

= ( da _x e _x + da ₂ e ₂ + da ₃ e ₃) •

= da _x e _x-- db _x e _x + db ₂ e ₂

db e                1 db e

—— + da 2e2----— dbxex           dbxex + db2e2 db2e2

+da 3e3-- dbxex + db2e2

db _x e _x + db ₂ e ₂

db _x e _x + db ₂ e ₂

da e • db e             da e • db e             da e • (db e + db e )

------—---L_!----+---- 22   22    +       33    11    22

( db _x e _x + db ₂ e ₂ ) • db _x e _x (db _x e _x + db ₂ e ₂ ) • db ₂ e ₂ (db _x e _x + db ₂ e ₂ ) • ( db _x e _x + db ₂ e 2 )

da _x db _x + da ₂ db ₂ = da _x + da ₂ db ₁²       db ₂²      db ₁ db ₂

Теорема доказана.

Аналогично доказывается следующая теорема.

Теорема 5. Имеет место формула:

1 da

da--= —x db1e1 db1 .

Пример 1. Тело массой m движется со скоростью

135 v = i -v + j— v + k— v.

33  3

В соответствии с [4; 5] интегральный (в смысле объемного интегрирования) вектор Умова в этом случае равен

При этом

1 du du y du 1        3        5        1

du = —- +--- +--- = —mv + mv +--mv = —mv dv dv dv dv 18      18      18      2

xyz

что является кинетической энергией.

Векторная производная вектора по другому вектору

Определение 5. Операция da x — db называется векторной производной векторного поля a по векторному полю b.

Теорема 6. Имеет место формула da x — = — db2

' da y db ^z

—

d ^) i J do^ db y J I db x

—

da_x Y

—- j + db , ^J

da

_V db y

—

dOy ' dbx x

k

Доказательство.

d a x — = d ( a_x i + a j + a_z k ) x d b        x y z

^{d (} b - i ⁺ b y j ⁺ b z ^k )

= ( da_x i + da y j + da , k ) x

db i + db , j + db k xyz

= da_x i x

•

+ da , j x ^y

db i + db, , j + db, k xyz

1 ( db y ! + db k 2 V db y j db , k

л

+

•

db i + db, j + db, k xyz

+ da z k x

•

db i + db , j + db, k xyz

1 f db_x i db k ) --— + —— +

2 V db_x i db , k J

1 f db - i ^db y ^j _

2 V db - i db y j ^

db j

= da x i x-------------- ^y -------------+ da x i x

2( db_x i + db j + db , k ) • db j

db_z k

2( db_x i + db y j + db z k ) • db z k

+

db i                             db k

- j x-----------------x---------------+ da,, j x-----------------z----------------+ y   2( dbx i + dby j + dbz k) • dbx i     y   2( dbx i + dby j + dbz k) • dbz k

+ da , k x

db_x i

2( db_x i + db y j + db , k ) • db_x i

db j

+ da к x----------- ^y----------

²    2( db_x i + db y j + db , k ) • db y j

da_x i x db y j da_x i x db , k da y j x db_x i da y j x db , k 2 db ^{2    +}    2 db!    ⁺   2 db_x 2   ⁺    2 db!

yz   x   z da, k x dbx i da, k x dby j +   2db^   +   2db^

xy

' ^da x ^db y

V db y

k

—

daxdbz

db

j

—

z

da y dbx    daydbz   da db    dazdby yk +y1 +,j1

db ²        db ²       db ²       db ²

x   zx   y

1 = 2	dax. 1 db x k	da --J — dbz	da y dbx	da da k + — y i + —- j		da --- i db , )	=
				dbz	dbx
1 ^	f da .	da Y	da	da	f	da„	1
= — 2 [	I dib. —	db , )' +	z . db x	x db z )	J Д db x	— db , 1 x	k J

Теорема доказана.

Представляет интерес частный случай, когда берется векторная производная по радиус-вектору r .

d a x — = d r

'd a y

5 z

—

dУ )

d a z

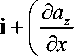
— da, | •

—- I + d z )

r

d a x

( 5y

—

dav)

k

5 x

)

—rot a = —V x a .

Следствие. Имеет место формализм:

d x — = d r

—

¹ Vx .

Приведенное выше замечание обусловливает следующие две теоремы.

Теорема 7. Имеет место формула

da x —— = -a3- e2

db e ₁ db

—

da

² e ₃, db

Доказательство.

da x —— = d (a1e1 + a 2e2 + a 3e3) x —— = (da1e1 + da 2e2 + da 3e3) x ^1- dbe1                           dbe1                             dbe1

1    db e              1    db e            1    db e

= da 1e1 x---1 + da2e2 x---1 + a3e3 x---1 = dbe1  dbe1           dbe1  dbe1         dbe1  dbe1

db e                db e               db e

= da1e1 x------1— + da2e2 x------1— + a3e3 x------1— db e1 • db e1            db e1 • db e1           db e1 • db e1

da , e, x db e, da, e₂ x db e, a ₃e₃ x db e, = —   .--- ¹ + — 22     1 - + -33     1

db ²            db ²           db ²

Теорема доказана.

Теорема 8. Имеет место формула

—

da ₂ db db ²

a db a e3 + 3 . e2 = — e2

³ db ^{2 2} db ²

—

da

2 e db ^{3 .}

d a x----------- d ( b ₁ e ₁ + b ₂ e ₂)

da

³ e ₁ 2 db ₂

da

+ —- e 2 db ₁

^{f d}a 1 da 2' [ db 2 db )

Доказательство.

da x---------------= d (a1e1 + a 2e2 + a 3e3) x--------------- d (b1e1 + b 2e2)                              d (b1e1 + b 2e2)

db ₁ e ₁ + db 2 e 2

= da 1 e 1 x

•

db 1 e 1 + db ₂ e ₂

db ₂ e ₂

db ₂ e ₂

+ da ₂ e ₂ x

•

db 1 e 1 + db ₂ e ₂

db e

—+ db ₁ e ₁

+ da 3 e 3 x

•

db 1 e 1 + db ₂ e ₂

1 f db ^ ₊ d^b 2 ^e 2 '

2 V db 1 e 1 db ₂ e _{2 7}

= da 1 e 1 x

db ₂ e ₂

( db 1 e 1 + db ₂ e ₂) • db ₂ e ₂

+ da ₂ e ₂ x

db ₁ e ₁

( db 1 e 1 + db ₂ e ₂) • db 1 e 1

+

+ da 3 e 3 x

db ₁ e ₁

2( db 1 e 1 + db ₂ e ₂) • db 1 e 1

+ da 3 e 3 x

db ₂ e ₂

2( db 1 e 1 + db ₂ e ₂) • db ₂ e ₂

da 1 e 1 x db ₂ e ₂

db 2     ⁺

da ₂ e ₂ x db ₁ e ₁

db ₁ ²

+

da ₃ e ₃ x db ₁ e ₁

2 db ₁ ²

da ₃ e ₃ x db ₂ e ₂

⁺     2 db 2     =

da db

1   2e db22

—

da ₂ db ₁ db ₁ ²

e ₃ +

da db

3    1 e

2 db ₁ ²

—

da ₃ b ₂

2 db ₂ ² e ¹ =

—

da ₃ 2 db ₂

da e. + —3

¹ 2 db ₁

e ₂ +

/

V

da ₁ db ₂

—

da ₂ db

^: 2 '

e ₃ .

1 7

Пример 2. Точка совершает вращательное движение с угловой скоростью w = ke и тангенциальным ускорением

. . s t2 , .s aT = —ia sin—+ ia cos—. T           22

Здесь k e – угловое ускорение. В соответствии с (3)

,        1      da Ty . da. .      . , - s t2    . 4s daT x — = —^i--— j = —iat sin— + iat cos— = v, d о  do,   do,           22

z

z

то есть результат является линейной скоростью точки.

Пример 3. Скорость точки равна v = — ioRsin ot + joR cos оt + ko2Rt, ускорение – a = —io2R cos оt — jo2R sin оt + ko2R .

В соответствии с (2)

d a x — = d v

1 da . da_x .

y i1 + dvz    dvz

г

V

da dv

x

—

da y _k

' dv y -'x 7

. o , . o .     , ,

— i —cos o t — i —sin o t — k o = — о 22

.