Скалярные мультикротовые норы

В общей теории относительности известны решения уравнений Эйнштейна, которые интерпретируются как гравитационное поле, создаваемое двумя и более точечными массами [1-4] (см. обзоры [5,6]). Кайгородовым в работе [3] был предложен следующий подход для получения метрики двух точечных масс: необходимо взять решение Шварцшильда, для одного центра, перевести его в осесимметричную вейлеву систему координат (0.8), затем в этой системе координат сдвинуть гравитационный заряд по оси z, сделав замену z ^ z — zi и получив таким образом поле точечного заряда, находящегося в точке zi. Решение для двух точечных масс можно получить из принципа суперпозиции, складывая гравитационные потенциалы частиц, находящихся в точках z1 и z₂. Этот подход может быть применен также для построения многочастичных решений с электрическими зарядами [7]. В пашей работе данный подход будет использован для построения решения, описывающего несколько кротовых пор в теории гравитации со скалярным полем.

Кротовыми норами в физической литературе называют туннели, связывающие удаленные области Вселенной или «мосты» соединяющие различные вселенные. На сегодняшний день кротовым порам посвящена, обширная литература: впервые подобные решения появились во времена. Эйнштейна [8,9], кротовые норы рассматривал в своей геометродинамике Уилер [10,11], Моррис, Торп и Юртсевер рассматривали «проходимые» кротовые поры [12], обзор исследований можно найти в работе [13]. Для существования кротовых пор требуется присутствие экзотической формы материи, нарушающей энергетические условия [12-15]. Одной из моделей такой материи является фантомное скалярное поле, которое допускает решения описывающие кротовые поры [16-20]. Наиболее исследованными являются статические, сферически симметричные кротовые поры в силу их более высокой симметрии. Одним из обобщением исследований является построение решений, описывающих несколько кротовых пор. В пашей работе построено решение, описывающее несколько кротовых пор в теории гравитации со скалярным полем. В этом параграфе рассмотрено статическое сферически-симметричиое решение кротовой поры в теории гравитации со скалярным полем [17,18], рассмотрена аксиально - симметричная метрика Вейля пространства-времени, выписаны уравнения Эйнштейна, и уравнение поля.

Рассмотрим теорию гравитации с безмассовым фантомным скалярным полем ф, описываемую действием следующего вида:

S = j d4xV—g(R + g^vV^Vvф),(0.1)

где g^_v — метрический тензор. R — скалярная кривизна. Вариация действия по метрике g^_v и полю ф приводит к уравнениям Эйнштейна и уравнению движения скалярного поля, соответственно:

R^v = -V^Vv ф,(0.2)

Vv Vv ф = 0.(0.3)

Приведем статическое сферически симметричное решение кротовой поры в теории гравитации с безмассовым фантомным скалярным полем [17,18]

ds2 = —e2udt2 + e 2u[dr2 + (r2 + a2)(dQ2 + sin2 0d^2)],                  (0.4)

21/2(m2 + a2)1/2

ф(г) = --------------------u(r),                                                    10-5)

m где r E (—го, +^). m. a — константы интегрирования ii u(r) = m (arctan Г — П2). Парамстр m является асимптотической массой кротовой порв:, которую видит удаленный наблюдатель в той части пространства, где координата r принимает положительное значение. Горловиной кротовой поры будем называть пространственную двумерную сферу r = 0. В случае m = 0 решение принимает особенно простой вид:

ds² = —dt² + dr² + (r² + a²)(dQ² + sin² 6d^²),

Ф ( г ) = V2 (

r arctan —

a

П).

(0.6)

(0.7)

Поле двух покоящихся гравитационных центров обладает осевой симметрией. В случае аксиально симметричных полей тяготения метрика пространства-времени может быть представлена в форме [5]4

ds² = — e^dt² + e^2(v-A)[dp² + dz²] + p²e^-2Ad^², (0.8)

где p E [0, +to). z E (—го, +го). у E [0, 2п) - цилиидрическне координаты, v и А - функции переменных p и z. Метрика (0.8) называется метрикой Вейля, координаты p, z, у будем называть координатами Вейля. Рассмотрим теорию гравитации (0.1) с фантомным скалярным полем ф = ф(p, z) в пространстве-времени, обладающем аксиальной симметрией и описываемом метрикой (0.8). По аналогии с [5], уравнения Эйнштейна и уравнение движения поля могут быть представлены в виде др — ^ДА + —1 ^ + A1 + а2 = 2 (ф1 + ф2) ,                    (0.9)

A1 — А2    1 = 9 (ф1 — ф2) ,                                       (0.10)

p2

2A1A2 — — = Ф1Ф2,                                            (0.П)

ρ

ДА + — = 0,                                             (0.12)

ρ

Дф + — = 0,                                             (0.13)

ρ где нижние индексы означают производные по координатам x1 = p, x2 = z, а Д = ——- + ——у-∂ρ2   ∂z2

Уравнения (0.9-0.12) являются независимыми комбинациями уравнений Эйнштейна, а (0.13) это уравнение скалярного поля. Уравнение (0.9) является дифференциальным следствием уравнений (0.10-0.13) системы. Условие интегрируемости уравнений (0.10, 0.11)

2A2

(ДА + А1^ + ф2 (дф + Ф1) = 0

(0.14)

является следствием уравнений (0.12, 0.13). В дальнейшем уравнения (0.12, 0.13) будем называть условием интегрируемости системы (0.10, 0.11). Таким образом, если найдены решения А и ф уравнений (0.12) и (0.13), то (0.10, 0.11) интегрируемы и функция v выражается криволинейным интегралом

v=

ρ

l

λ21

λ22

2 (ф1— ф2) dp

— p [2А1А2

— ф1ф2] dz

(0.15)

по произвольному непрерывному пути 1, соединяющему некоторую фиксированную точку (po,zo) с точкой (p, z). Выбор (p0, z0) определяется граничным и условиями на. функцию v. Так как уравнения (0.12, 0.13) линейны по функциям А и ф, значит любая линейная комбинация с постоянными коэффициентами нескольких решений A(k) и ф(к) этих уравнений А = ^ A(k). ф = ^ ф(к) снова будет их решением. Далее, по суперпозированным А и ф можно найти отвечающую им функцию v из (0.15), то есть получить новое решение.

• 1.    Суперпозиция решений кротовых нор

В этом параграфе будут приведены преобразования, связывающие координаты Вейля и сферические координаты, метрика сферически симметричной кротовой поры будет представлена в аксиально симметричном виде в координатах Вейля, будет произведено сложение двух решений, описывающих кротовые норы в теории гравитации со скалярным полем. Сферически-симметричная

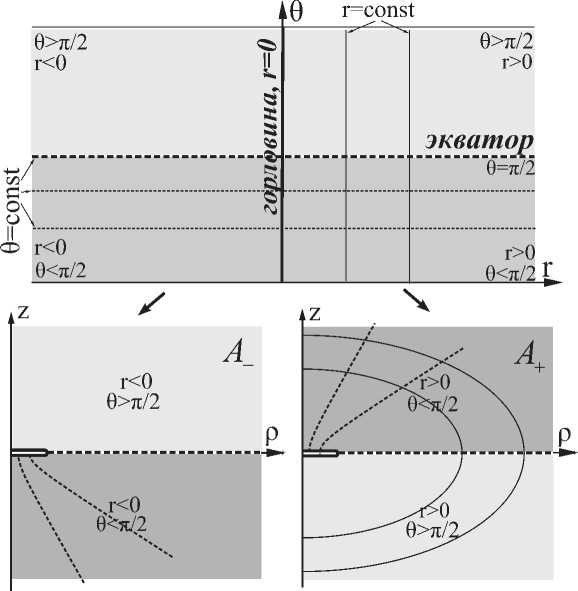
Рис. 1. Рисунок иллюстрирует преобразование координат (1.1): (r, 6) ^ (р, z). Вверху изображена область изменения координат (r, 6), это бесконечная полосы шириной п, горловине соответствует вертикальный отрезок r = 0, 6 Е [0, п). В вейлевых координатах (р, z) пространство описывастся двумя картами: A+ покрывает область с r >  0, A- - область с r <  0. Области изменения координат (р, z) - nu/iyn/юскости. Липпи r = const в координатах (р, z) являются полуэллипсами, линии 6 = const - гиперболами. Граница карт проходит по горловине, которая соответствует двустороннему отрезку z = 0, р Е [0, а].

метрика является частным случаем более общей, аксиально-симметричной метрики пространства-времени. Следовательно статическое сферически-симметричиое решение (0.4, 0.5), описывающее кротовую пору, может быть представлено в аксиально-симметричном виде (0.8). Координатные преобразования, связывающие сферические координаты (r, 9, у) и координаты Вейля (р, z, у) имеют вид

( p(r,9) = Vr² + a² sin 9, [ z(r, 9) = r cos 9.

(1.1)

Преобразование временной координаты t и полярного угла у тождественные. Координаты пробегают следующие интервалы значений:

r ∈

(-то, то),    9 Е [0, п];

(1.2)

р Е [0, то),    z Е (-то, то).

(1.3)

Диапазон изменения координат (r, 9) в декартовых координатах представляет собой бесконечную полосу шириной п, диапазон изменения координат (р, z) — полуплоскость. Преобразование координат (1.1) неоднозначно в указанных областях и отождествляет точки (t,r, 9,^) ~

(t, —r,n — 6,^). Преобразование станет однозначным, если, например, ограничится рассмотрением области пространства-времени A+ := {(t,r, 6,^) | r > 0} или, наоборот, области А- := {(t, r, 6, у) | r < 0}. Мы получаем набор из двух карт: карта A+ покрывает область пространства с r > 0, a A- покрывает область с r < 0. Приведем обратное координатное преобразование f r = ±2-1/2 [р2 + z2 — a2 + [(р2 + z2 — a2)2 — 4a2z2] 1/21 1/2 , z

I 6 = arccos —---), где знак «+» в выражении для <|>yiiKiiiiii r(p, z) соответств} тт области A+- «—» - об ласти А-. Якобиан преобразования

D(р, z)    r² + a² cos² 6

D(r, 6) = (r2 + a2)1/2

обращается в ноль при r = 0, 6 = п/2, что соответствует линии экватора горловины кротовой поры.

Решение, описывающее сферически симметричную кротовую нору (0.4) в координатах Вейля принимает вид:

ds² = —e^2A± dt² + e^2(v± ^A±⁾[dр² + dz²] + р²е ^2A±d^²,

A± = m arcctg r^, aa

_ 1    r± (р, z)(r²(р, z) + a²)

V±    О ln 4 /    \ I 22    ,

2 r± (р, z) + a²z²

(1-5)

(1-6)

(1-7)

ф± = //2(m2 + a2) m 1А±.

где решение с индексом «+» соответствует карте A+ (r > 0), решение с индексом « —» - A_ (r < 0). Функции r+ 11 r- равны

• r±(p, z) = ±2^-1/2 [р² + z² — a² + [(р² + z² — a²)² — 4a²z²] 1/2]    .                 (1.8)

При переходе через границу двух карт ( r = 0) решение (1.5-1.7) для A- непрерывно и гладко переходит в решение для A+. Характер координатного преобразования поясняется на рис. 1. Граница карт A+ и A- проходит по горловине кротовой поры r = 0. Горловина кротовой поры при этом преобразование переходит в двусторонний диск: z = 0, р Е [0, a], на плоскости (р, z) ему соответствует двухсторонний отрезок. Для прояснения топологической структуры па рисунке изображены несколько координатных линий: линии r = const, которым соответствуют тонкие сплошные кривые, и линии 6 = const, обозначенные штрихпунктирными кривыми. Линии r = const в координатах (р, z) переходят в полуэллипсы, причем каждая координатная линия расположена целиком в одной из карт. Линии 6 = const в координатах (р, z) преобразуются в гиперболы, причем, так как координатные линии проходят сквозь горловину кротовой поры, то они располагаются в обоих картах. Как и следовало ожидать, скалярная кривизны метрики (1.5) в координатах Вейля

R =

2(m2 + a2)e2A(p,z) (r2(р,z) + a2)2 ,

(1.9)

и всюду ограничена, на горловине r = 0 (р Е [0, a], z = 0) равна 2(m2 + a2)e-na-4.

Уравнения Эйнштейна и уравнение поля не содержат явно координаты z, поэтому после замены z щ z — zo в решении (1.5), получим новое решение, описывающее сферически симметричную кротовую пору, помещенную в точку со значением zo на оси z. Будем далее обозначать функции А. отвечающую решению кротовой норы с асимптотической массой m и параметром горловины a. помещенную в точку zo ос и z, записанной в вейлевой системе координат, через А(р, z, zo, m, a), или короче A(zo,m, a), указывая лишь значения параметров, т.е.

А(zo,m.a) = marcctg ^{г ( р} , z — z ^{o )} , aa

(1.10)

где r (р, z — zo) имеет вид r (р, z — zo) = ±2-1/2 [р2 + (z — zo)2 — a2 + [(р2 + (z — zo)2 — a2)2 — 4a2(z — zo)2] 1/2]    .

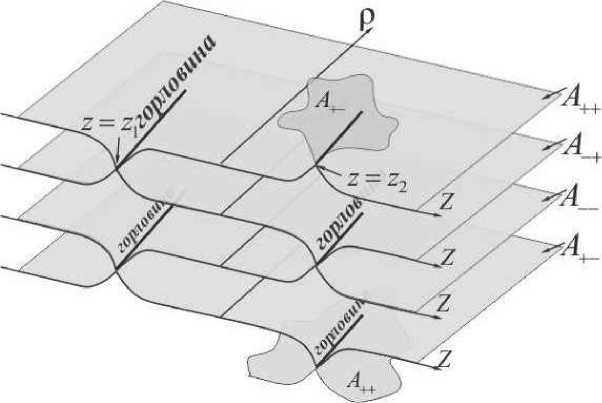
Рис. 2. Геометрия пространства двух кротовых нор (координатная поверхность р и z, сечение t = const, у = const).

Уравнения (0.12, 0.13) линейны по функциям А и ф, значит любая линейная комбинация с постоянными коэффициентами нескольких решений А^(к) и ф^(к) этих уравнений А = ^ А^(к). ф = ^ ф^(к) снова будет их решением. Далее, по этим значениям А и ф можно найти отвечающую им функцию v (0.15), то есть получить новое решение уравнений. Осуществим сложение решений для случая двух произвольный сферически симметричных кротовых пор (1.5-1.6) с асимптотическими массами mi 11 m2 и параметрамш горловины a_i i1 a₂. находящихся в точках z_i i1 z₂ oф пропорционально гравитационному потенциалу А, рассмотрим сложение гравитационных потенциалов, предполагая для скалярного поля справедливым тот же закон сложения, что и для А. Следуя [4], сложение можно осуществить, если взять такое правило

А = kiА±(zi, m = mi + m2, ai) + k2А±(z2, m = mi + m2, 02),                (1-H)

где k_i. k₂ - числа, удовлстворятощие условию k_i + k₂ = 1. Тогда. при zk ^ z₀ 11 ak ^ a. очевидно, получим

А = (k_i + k₂)А±(zo, m = m_i + m₂, a) = А±(zo, m = m_i + m₂, a),               (1.12)

т.е. получим решение для сферически симметричной кротовой поры с асимптотической массой m = m_i + m₂, помещенной в точке z = 0. Выбор коэс)>фициентов k_i и k₂, которые будем называть весовыми [4], вообще говоря, произволен (лишь бы k_i + k₂ = 1), 110 надо потребовать, чтобы выполнялись условия:

при m_i = 0. m2 = 0 должио быть k_i = 0. k₂ = 1,                 (1-13)

при mi = 0. m2 = 0 должио быть ki = 1. k2 = 0.                 (1-14)

Следуя [4], выберем их такими mi ki = ------:------, mi + m2

m2

k2 =---7--- mi + m2

.

(1-15)

Для скалярного поля возьмем такое же правило сложения ф = kiф±(zi, m = mi + m2, ai) + k2ф±(z2, m = mi + m2, a2).

(1.16)

Подставляя функции А и ф в (0.15), найдем функцию v.

Каждое из исходных решений описывалось двумя функциями А, а именно А . и А-. Поэтому для суммарного гравитационного потенциала А (2.16) получаем четыре различные комбинации из функций А+ (zk,m, ak) и А-(zk,m, ak) (k = 1,2) (и аналогичные комбинации для скалярного

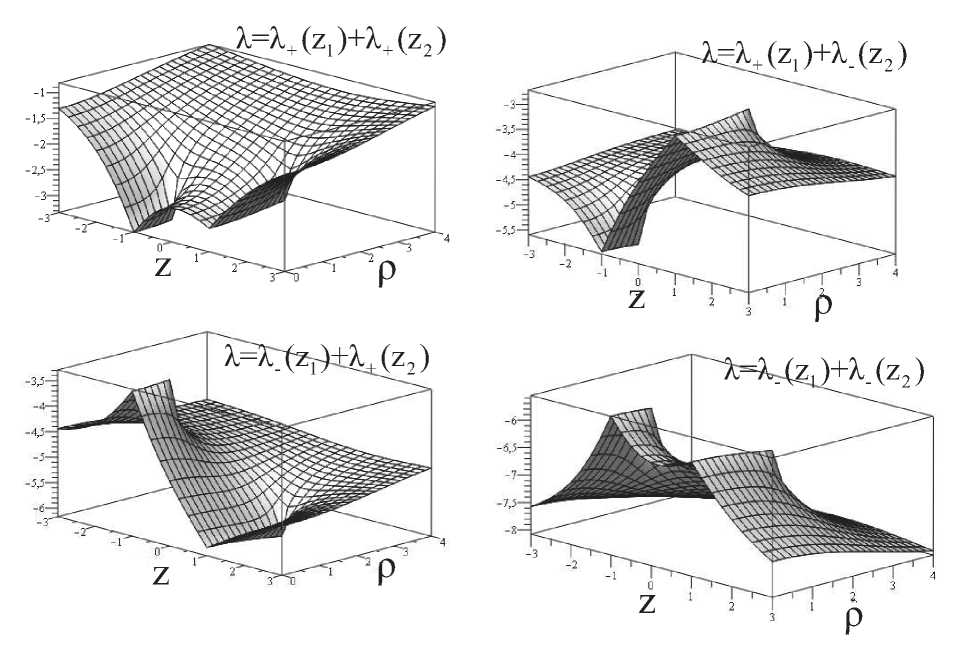
Рис. 3. Гравитационный потенциал A(p,z) в областях A++: А = A+(zi) + A+(z2), A + А = A-(zi) + A+(z2), A+ : А = A+(zi) + A_(z2). A : A = A_(zi) + A_(z2) в случас zi = — 1. Z2 = 1. ai = 1. a2 = 2. m = 1.

поля), и четыре различных решения для функции v (0.15) для каждой комбинации соответственно. Введем обозначение:

А(±,±) = kiA±(zi, m = mi + m2, ai) + k2A±(z2, m = mi + m2, 02)- (1-17)

Возникает вопрос, как полученные для каждой из комбинаций А(±,±) решения будут связаны друг с другом? Пространство каждой из исходных кротовых пор в вейлевых координатах описывалось двумя картами. A₊ :1 A-. Пересекая горловину кротовой норы, мы попадаем ыз области А₊ в область A-, при этом значение гравитационного потенциала в области А₊ описывалось функцией А₊, в об ласти А_- оно будет опись: ваться функцией А-. Гравитационный потенциал при переходе с карты на карту через горловину меняется непрерывно и гладко. Требование непрерывности функции А приводит к такому же правилу для суммы двух решений. Допустим, что мы находимся в области, где гравитационный потенциал имеет значение А(₊,₊) = k_iA+(z_i,a_i) + k₂A+(z₂,a₂). Пересекая горловину первой кротовой поры (расположенной в точке z = z_i) соответствующее ей слагаемое в гравитационном потенциале должен изменить свое значение с А+ (z_i, a_i) и a A_-(z_i, a_i). Таким образом горловина первой кротовой поры соединяет решение для А(₊,₊) с решением для А(-,₊). Рассуждая аналогичным образом, получим, что горловина второй кротовой поры соединяет решение для А(-,₊) с решением для А(-,-); горловина первой кротовой поры соединяет решение для А(-,-) с решением для А(₊,-); и, наконец, горловина второй кротовой поры соединяет решение для А(₊,-) с решением для А(₊,₊). Таким образом, мы получим набор из четырех карт соответствующих четырем комбинациям гравитационного потенциала⁵ (2.16). Карту, описывающую решение для А(±,±) обоз::ачим A±±. В каждой карте расположены две горловины, т.е. удаленный наблюдатель в каждой из областей A±± видит две кротовые поры. Во всем пространстве времени мы имеем

• ⁶ Совпадение гравитационного потенциала нс означает, что мы оказались в той же области пространства. Нс исключено, что это новая, ранее нс рассматриваемая область пространства, но с тем же значением величин A и ф. В общем случае мы получим набор из 4k карт (k = 1, 2,...) или бесконечного набора карт.

  

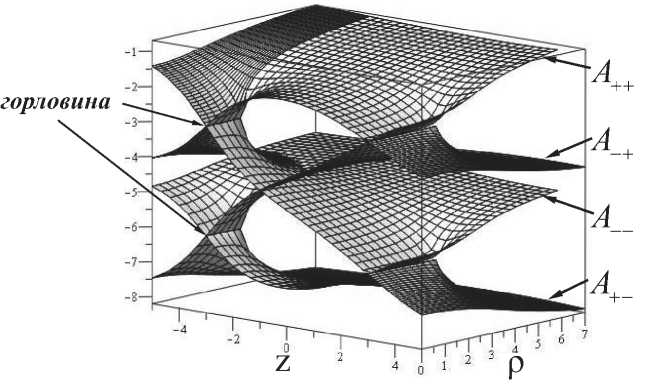
  Рис. 4. На рисунке представлена функция гравитационного потенциала А(р, z) одновременно для четырех карт A++. A у. A+ A в елучае z 1 = —3, z ₂ = 3, a1 = 1.5, a ₂ = 3, m = 1.

  
  

четыре кротовые поры. Границы карт проходят по горловинам кротовых пор. Рис. 2 иллюстрирует топологическую структуру многообразия. При переходе с карты па. карту гравитационный потенциал и функция скалярного поля ведут себя непрерывно и гладко. График функции скалярного поля А(р, z) для каждой из карт приведен на. j hic. 3. 4. график скалярного поля ф(р, z) имеет аналогичный вид.

Функция v(р, z) определяется выражением (0.15). Потребуем выполнение следующего граничного условия:

v(р   I ж, z   I ж) 0 в об ласти A₊₊,                        (1-18)

что соответствует р₀ = +ж, z₀ = I ж в (0.15). В случае, если (р, z) Е A++, то кривая интегрирования l может быть расположена в области A++, в качестве кривой удобно взять ломанную

R v(R,z) = Jr

ρ 0

А1

а2

z

2 (^ф1^{— ф}2) ^dр - j ^р [2А1А2

- Ф1Ф2] dz

(1-19)

z 0

Р=Р 0

В случае, если (р, z) расположена, в другой карте многообразия. кривая интегрирования l будет переходить с карты на карту. Вследствие этого значение функции v на бесконечности р ^ ж, z ^ ж в картах A у, Ay , A могут отличаться от нуля на некоторое постоянное значение. Получим

R

v(R,z) = У R

ρ 0

А1

А2

z

2 (^ф1 ^{— ф}2) ^{dр —} У ^{р [}2А1А_:

Ф1Ф2] dz

+ v (рo,zo),

(1.20)

где v(рo,zo) = 0 в случае (р, z) Е A++- Функция v приведена на рис. 5. Отметим, что разрывы функции по обе стороны от горловин в карте A++ и A __у отличаются только знаком и равны по абсолютной величине, что обеспечивает непрерывность функции v при переходе из одной карты в другую. В силу четности v относительно А и ф ее значения в области A++ совпадают со значениями в области A а. знамения в области A у - со значсинями в Ay

В заключение этого раздела, отметим, что данный подход позволяет получить решение, описывающее произвольное число кротовых пор, расположенных на оси z. Рассмотрим суперпозицию n кротовых пор, для этого возьмем n сферически симметричных решения, расположенных в точках zs (s = 1,... n) на оси z. Для гравитационного потенциала выберем закон сложения n                       nm

.

(1.21)

А =     ksA±(zs,m, as), где m = £ ms. ks = —

“                  s=1        m

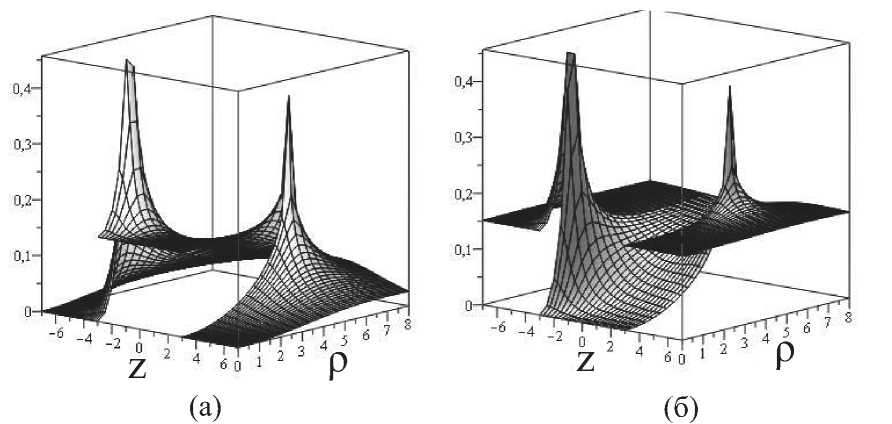
Рис. 5. График функции v(p,z) в областях A++, A (рис. а), в областях A + A+- (рис. б) в случае mi = 1, m2 = 2. ai = 1.5. a2 = 5. zi = —3. Z2 = 3.

В этом случае мы будем иметь 2ⁿ различных комбинаций для А и ф, для каждого из которых функция v(р, z) определяется выражением (0.15). Координатную область каждого решения обозначим как A±...±, в результате получим набор 2ⁿ карт. Каждая из карт соединена через горловины кротовых нор с другими картами пространства. Например, пересекая горловину кротовой норы, расположенной в точке z1 о си z мы из области A+... попадем в область A-....

Заключение

Получено решение, описывающее две кротовые поры в теории гравитации с фантомным скалярным полем в аксиально симметричном пространстве-времени. Для построения решения был использован следующий подход: взято решение, описывающее статическую сферически симметричную кротовую нору в теории гравитации со скалярным полем (0.4, 0.5), решение было представлено в осесимметричной вейлевой системе координат (1.5-1.7), затем в этой системе координат центр решения был сдвинут по оси z посредством замены z ^ z — z₀, в результате получено поле сферически симметричной кротовой поры, находящейся в точке z₀ о си z. Далее, складывая гравитационные потенциалы A(zk ,m,ak) (к = 1, 2) для двух кротовых пор, находящихся в точках z1 и z₂ (2.16), получено решение для двух покоящихся кротовых пор. Полученное решений описывается набором из четырех карт, решение обладает четырьмя плоскими асимптотиками. Аналогичным образом построено аксиально симметричное решение, описывающее n кротовых пор. В этом случае пространство-время обладает 2ⁿ различными асимптотически плоскими областями.