Skin Diseases Expert System using Dempster-Shafer Theory
Автор: Andino Maseleno, Md. Mahmud Hasan
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 5 vol.4, 2012 года.
Бесплатный доступ
Based on World Health Organization (WHO) report in the 2011 Skin diseases still remain common in many rural communities in developing countries, with serious economic and social consequences as well as health implications. Directly or indirectly, skin diseases are responsible for much disability (and loss of economic potential), disfigurement, and distress due to symptoms such as itching or pain. In this research, we are using Dempster-Shafer Theory for detecting skin diseases and displaying the result of detection process. We describe five symptoms as major symptoms which include blister, itch, scaly skin, fever, and pain in the rash. Dempster-Shafer theory to quantify the degree of belief, our approach uses Dempster-Shafer theory to combine beliefs under conditions of uncertainty and ignorance, and allows quantitative measurement of the belief and plausibility in our identification result. The result reveal that Skin Diseases Expert System has been successfully detecting skin diseases and displaying the result of identification process.
Skin diseases, expert system, Dempster-Shafer theory
Короткий адрес: https://sciup.org/15010254
IDR: 15010254
Текст научной статьи Skin Diseases Expert System using Dempster-Shafer Theory
Published Online May 2012 in MECS
Skin diseases are a bit like the common cold. Apart from some of the skin cancers, they are not recorded in any official registry. They vary enormously from mild conditions which may affect only the appearance of the skin to severe diseases which are totally incapacitating. The degree of treatment required, or even sought, varies accordingly [1]. What makes the skin unique among organs is its exposed position up against the outside world. Other body organs can function only in a controlled, protected environment where the temperature never varies far from 98.6 degrees Fahrenheit. The skin maintains this environment, and to do so, it must be able to take on temperatures ranging from dry desert heat to bitter cold. It must be exquisitely sensitive to its surroundings: when the outside temperature rises, blood flow through the skin must increase and sweat glands must secrete liquid whose evaporation will keep the inner temperature from also rising; when the temperature dips, vessels must constrict to conserve body heat [2].
In terms of previous work using Dempster-Shafer theory, some works for diagnosis in skin diseases have been developed which were system for differential diagnosis of erythemato-squamous diseases incorporating decisions made by three classification algorithms: nearest neighbor classifier, naive Bayesian classifier and voting feature intervals-5 [3], system achieved with the import of certain medical cases [4] and to help dermatologists in diagnosing some of the skin diseasess [5]. Actually, according to researchers knowledge, Dempster-Shafer theory of evidence has never been used to built a system for detecting skin diseases.
This paper is organized as follows. Section 2 details the proposed Dempster-Shafer Theory in detecting skin diseases. Software implementation in Section 3, and conclusion in Section 4.
-
II. DEMPSTER-SHAFER THEORY AND DETECTION PROCESS
The Dempster-Shafer theory was first introduced by Dempster [6] and then extended by Shafer [7], but the kind of reasoning the theory uses can be found as far back as the seventeenth century. This theory is actually an extension to classic probabilistic uncertainty modeling. Whereas the Bayesian theory requires probabilities for each question of interest, belief functions allow us to base degrees of belief for on question on probabilities for a related question. Even though DST was not created specially in relation to artificial intelligence, the name Dempster-Shafer theory was coined by J. A. Barnett [8] in an article which marked the entry of the belief functions into the artificial intelligence literature. The Dempster-Shafer theory or the theory of belief functions is a mathematical theory of evidence which can be interpreted as a generalization of probability theory in which the elements of the sample space to which nonzero probability mass is attributed are not single points but sets. The sets that get nonzero mass are called focal elements. The sum of these probability masses is one, however, the basic difference between Dempster-Shafer theory and traditional probability theory is that the focal elements of a Dempster-Shafer structure may overlap one another. The Dempster-Shafer theory also provides methods to represent and combine weights of evidence.
-
m: 2Θ → [0,1] is called a basic probability assignment (bpa) over Θ if it satisfies
m (Ø) = 0 and
V m (5) = 1 (1)
From the basic probability assignment, the upper and lower bounds of an interval can be defined. This interval contains the precise probability of a set of interest and is bounded by two nonadditive continuous measures called Belief (Bel) and Plausibility (Pl). The lower bound for a set A, Bel(A) is defined as the sum of all the basic probability assignments of the proper subsets (B) of the set of interest (A) (B ⊆ A ). Formally, for all sets A that are elements of the power set, A ∈ 2Θ m (S) = 1 (2)
A function PL: 2Θ →[0,1] is called a plausibility function satisfying
£ ™(B) (3)
5П4*0
The plausibility represents the upper bound for a set A , and is the sum of all the basic probability assignments of the sets ( B ) that intersect the set of interest ( A ) ( B ∩ A ≠φ ). The precise probability P(A) of an event (in the classical sense) lies within the lower and upper bounds of Belief and Plausibility , respectively:
Bel( A ) ≤ P ( A ) ≤ PL ( A ) (4)
The advantages of the Dempster-Shafer theory which include the ability to model information in a flexible way without requiring a probability to be assigned to each element in a set, providing a convenient and simple mechanism (Dempster's combination rule) for combining two or more pieces of evidence under certain conditions, it can model ignorance explicitly, rejection of the law of additivity for belief in disjoint propositions. Flowchart of skin diseases detection shows in Figure 1.
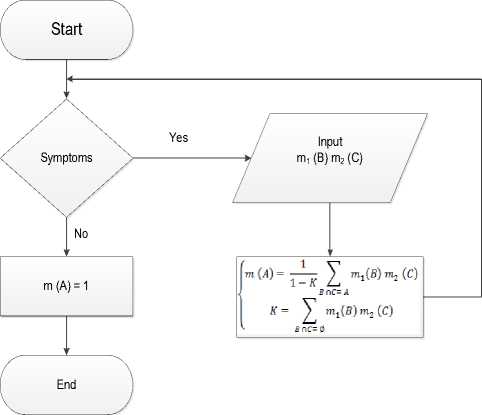
Figure 1. Flowchart of skin diseases expert system
The detection process begins with selecting the symptoms. If there are symptoms then will calculate, The Dempster-Shafer theory provides a rule to combine evidences from independent observers and into a single and more informative hint. Evidence theory is based on belief function and plausible reasoning. First of all, we must define a frame of discernment, indicated by the sign Θ . The sign 2Θ indicates the set composed of all the subset generated by the frame of discernment. For a hypothesis set, denoted by A, m(A)→[0,1].
TABLE 1. BASIC PROBABILITY ASSIGNMENTS OF EACH SYMPTOM
|
No. |
Symptom |
Disease |
Basic probability assignment |
||||
|
Condition |
Condition 1 |
Condition j |
Condition 4 |
Condition 5 |
|||
|
1 |
Blister |
Creeping Eruption |
0.8 |
0.7 |
0.6 |
O.4 |
03 |
|
2 |
Itch |
Creeping Eruption |
0.7 |
0.6 |
0.4 |
03 |
0.8 |
|
Dermatitis EksfoliatifGeneialisata |
|||||||
|
Impetigo |
|||||||
|
Pitriasis Rosea |
|||||||
|
• |
Scaly skill |
Creeping Eruption |
0.6 |
0.4 |
03 |
0.8 |
0.7 |
|
Dermatitis EksfoliatifGeneialisata |
|||||||
|
Pitriasis Rosea |
|||||||
|
4 |
Fever |
Dermatitis EksfoliatifGeneialisata |
0.4 |
03 |
0.8 |
0.7 |
0.6 |
|
Erisipelas |
|||||||
|
Nekrolisis Epidermal Toksika |
|||||||
|
5 |
Pain in the rash |
Erisipelas |
03 |
0.8 |
0.7 |
0.6 |
0.4 |
Suppose we are given five basic probability assignments of symptom from each condition as shown in Table 1. The following will be shown diagnosing skin diseases using Dempster-Shafer theory.
Symptoms:
-
1. Blister
-
2. Itch
-
3. Scaly skin
-
4. Fever
-
5. Pain in the rash
-
A. Symptom 1 - Blister
Blister is a symptom of Creeping Eruption (CE). The measures of uncertainty, taken collectively are known in Dempster-Shafer Theory terminology as a ``basic probability assignment'' (bpa ). Hence we have a bpa, say m1 of 0.8 given to the focal element {CE} in example, m 1 ({CE}) = 0.8, since we know nothing about the remaining probability it is allocated to the whole of the frame of the discernment in example, m 1 ({CE}) = 0.2, so:
m 1 {CE} = 0.8
m 1 {Θ} = 1 – 0.8 = 0.2 (5)
-
B. Symptom 2 - Itch
Itch is the symptom of Creeping Eruption (CE), Dermatitis Eksfoliatif Generalisata (DEG), Impetigo (I), and Pitriasis Rosea (PR) with a bpa of 0.7, so that:
m 2 {CE, DEG, I, PR} = 0.7
m 2 { Θ} = 1 – 0.7 = 0.3 (6)
We combine two symptoms which include blister and itch as shown in table 2.
TABLE 2. COMBINATION OF SYMPTOM 1 AND SYMPTOM 2
|
{ CE, DEG, I, PR} |
0.7 |
Θ |
0.3 |
||
|
{CE} |
0.8 |
{CE} |
0.56 |
{CE} |
0.24 |
|
Θ |
0.2 |
{ CE, DEG, I, PR} |
0.14 |
Θ |
0.06 |
We then calculate the combined of equation (5) and equation (6) as shown in the equation (7).
0.56 + 0.24
m3 {CE} = --------- = 0.8
1 - 0
m 3 {CE, DEG, I, PR}= 0.14 = 0.14
1 - 0
m 3 {0} = 0106 = 0.06
1 - 0
-
C. Symptom 3- Scaly Skin
Scaly skin is the symptom of Creeping Eruption (CE), Dermatitis Eksfoliatif Generalisata (DEG), and Pitriasis Rosea (PR) with a bpa of 0.6, so that:
m 4 {CE, DEG, PR} = 0.6
m 4 { Θ} = 1 – 0.6 = 0.4 (8)
We combine three symptoms which include blister, itch and scaly skin as shown in table 3.
TABLE 3. COMBINATION OF SYMPTOM 1, SYMPTOM 2, AND SYMPTOM 3
|
{ |
CE, DEG, PR} |
0.6 |
Θ |
0.4 |
|
|
{CE} |
0.8 |
{CE} |
0.48 |
{CE} |
0.32 |
|
{CE, DEG, I, PR} |
0.14 |
{CE, DEG, PR } |
0.084 |
{CE, DEG, I, PR} |
0.056 |
|
Θ |
0.06 |
{CE, DEG, PR } |
0.036 |
Θ |
0.024 |
We then calculate the combined of equation (7) and equation (8) as shown in the equation (9).
0.48 + 0.32 m5 {CE} = --------- = 0.8
1 - 0
0.084 + 0.036
m5 {CE, DEG, PR} = -----------= 0.12
1 - 0
m5 {CE, DEG, I, PR} = 01056 = 0.056
1 - 0
Ш 5 {0} = 0024 = 0.024
1 - 0 (9)
-
D. Symptom 4 - Fever
Fever is a symptom Erisipelas (E), Dermatitis Eksfoliatif Generalisata (DEG), and Nekrolisis Epidermal Toksika (NET), so that:
m 6 (E, DEG, NET) = 0.4
m 6 (Θ) = 1 – 0.4 = 0.6 (10)
We combine four symptoms which include blister, itch, scaly skin and fever as shown in table 4.
TABLE 4. COMBINATION OF SYMPTOM 1, SYMPTOM 2, SYMPTOM 3, AND SYMPTOM 4
|
{DEG, E, NET} |
0.4 |
Θ |
0.6 |
||
|
{CE} |
0.8 |
Ø |
0.32 |
{CE} |
0.48 |
|
{CE, DEG, PR} |
0.12 |
{DEG} |
0.048 |
{CE, DEG, PR} |
0.072 |
|
{CE, DEG, I, PR} |
0.056 |
{DEG} |
0.022 |
{CE, DEG, I, PR} |
0.033 |
|
Θ |
0.024 |
{DEG, E, NET} |
0.009 |
Θ |
0.014 |
We then calculate the combined of equation (9) and equation (10) as shown in the equation (11).
m7 (CE) = 0.48 = 0.705
1 - 0.32
0.048 + 0.022 .
m7 (DEG) = -----------= 0.102
1 - 0.32
m7(CE, DEG, PR) = 0.0/2 = 0.105
1 - 0.32
m7 (CE, DEG, I, PR) = 0.033 = 0.048
1 - 0.32
m 7 (DEG, E, NET) = 0.009 = 0.013
1 - 0.32
m 7 ( 0 ) =__________ 0010__________
1 - (0.212 + 0.031 + 0.032 + 0.014)
= 0.021
m7 (0) =
0.014
1 - 0.32
= 0.021
E. Symptom 5 – Pain in The Rash
Pain in the rash is symptom of Erisipelas (E) with a bpa of 0.3, so that:
m 8 {E} = 0.3
m 8 {0} = 1 - 0.3 = 0.7 (12)
We combine four symptoms which include blister, itch, scaly skin, fever and pain in the rash as shown in table 5.
TABLE 5. COMBINATION OF SYMPTOM 1, SYMPTOM 2, SYMPTOM 3, SYMPTOM 4, AND SYMPTOM 5
|
{E} |
0.3 |
{0} |
0.7 |
||
|
{CE} |
0.705 |
Ø |
0.212 |
{CE} |
0.494 |
|
{DEG} |
0.102 |
Ø |
0.031 |
{DEG} |
0.071 |
|
{CE, DEG, PR} |
0.105 |
Ø |
0.032 |
{CE, DEG, PR} |
0.074 |
|
{CE, DEG, I, PR} |
0.048 |
Ø |
0.014 |
{CE, DEG, I, PR} |
0.034 |
|
{DEG, E, NET} |
0.013 |
{E} |
0.004 |
{DEG, E, NET} |
0.009 |
|
{0} |
0.021 |
{E} |
0.006 |
{0} |
0.015 |
The highest bpa value is the m 9 (CE) that is equal to 0.695 which means the possibility of a temporary diseases with symptoms of Blister, Itch, scaly skin, fever, pain in the rash is the Creeping Eruption. Table 6 shows final result of basic probability assignments of each condition. Figure 2 through figure 6 are shown graphic of detection from each condition.
TABEL 6. FINAL RESULT
|
No. |
Disease |
Basic Probability Assignment |
||||
|
Condition 1 |
Condition 2 |
Condition j |
Condition 4 |
Condition 5 |
||
|
1 |
Creeping Eruption |
0.695 |
0.163 |
0.146 |
0.143 |
0.142 |
|
2 |
Dermatitis Eksfoliatif Generalisata |
0.099 |
0.022 |
0.226 |
0.426 |
0.466 |
|
3 |
Erisipelas |
0.014 |
0.095 |
0.479 |
0.149 |
0.032 |
|
4 |
Creeping Eruption |
0.104 |
0.028 |
0.03 |
0.17 |
0.231 |
|
Dermatitis Eksfoliatif Generalisata |
||||||
|
Pitriasis Rosea |
||||||
|
5 |
Creeping Eruption |
0.048 |
0.253 |
0.027 |
0.013 |
0.079 |
|
Dermatitis Eksfoliatif Generalisata |
||||||
|
Impetigo |
||||||
|
Pitriasis Rosea |
||||||
|
6 |
Dermatitis Eksfoliatif Generalisata |
0.013 |
0.008 |
0.162 |
0.07 |
0.031 |
|
Erisipelas |
||||||
|
Nekrolisis Epidermal Toksika |
||||||
We then calculate the combined of equation (11) and equation (12) as shown in the equation (13).
0.494
m 9 (CE) = ------------------------------= 0.695
1 - (0.212+ 0.031 + 0.032 + 0.014)
0.071
m 9 (DEG) = ---------------------------- = 0.099
1 - (0.212+ 0.031 + 0.032 + 0.014)
0.004 + 0.006
m9 (E) = -------------------------------= 0.014
1 - (0.212+ 0.031 + 0.032 + 0.014)
m 9 (CE, DEG, PR) =
0.074
1 - (0.212 + 0.031 + 0.032 + 0.014)
= 0.104
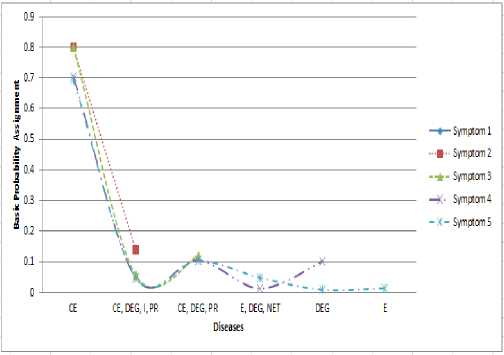
Figure 2 . Condition 1 (Creeping Eruption as the highest basic probability assignment).
m 9 (CE, DEG, I, PR) =
0.034
1 - (0.212 + 0.031 + 0.032 + 0.014)
m 9 (DEG, E, NET) =
0.009
1 - (0.212 + 0.031 + 0.032 + 0.014)
= 0.048
= 0.048
Figure 2 shows the graphic of Condition 1, we get the highest basic probability assignment is CE (Creeping Eruption) that is equal to 0.695 which show from the last calculation of Dempster-Shafer on symptom 5 which means the possibility of a temporary diseases with symptoms of blister, itch, scaly skin, fever, pain in the rash is the Creeping Eruption.
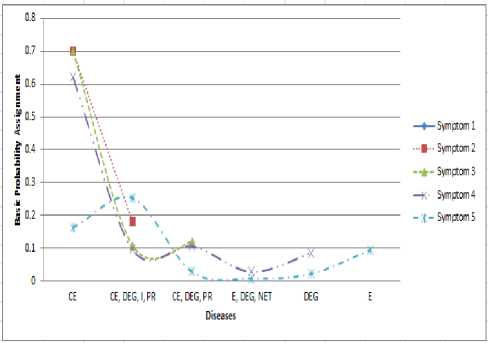
Figure 3. Condition 2 (Creeping Eruption, Dermatitis Eksfoliatif Generalisata, Impetigo, and Pitriasis Rosea as the highest basic probability assignment)
Figure 3 shows the graphic of Condition 2, We get the highest basic probability assignment are Creeping Eruption, Dermatitis Eksfoliatif Generalisata, Impetigo, and Pitriasis Rosea that is equal to 0.253 which show from the last calculation of Dempster-Shafer on symptom 5 which means the possibility of a temporary diseases with symptoms of blister, itch, scaly skin, fever, pain in the rash are Creeping Eruption, Dermatitis Eksfoliatif Generalisata, Impetigo, and Pitriasis Rosea.
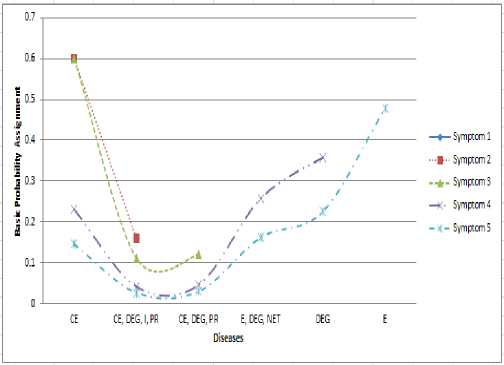
Figure 4. Condition 3 (Erisipelas as the highest basis probability assignment)
Figure 4 shows the graphic of Condition 3, we get the highest basic probability assignment is Erisipelas that is equal to 0.479 which show from the last calculation of Dempster-Shafer on symptom 5 which means the possibility of a temporary diseases with symptoms of blister, itch, scaly skin, fever, pain in the rash is the Erisipelas.
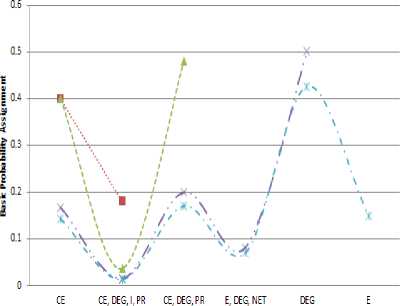
Figure 5. Condition 4 (Dermatitis Eksfoliatif Generalisata as the highest basic probability assignment)
Figure 5 shows the graphic of Condition 4, we get the highest basic probability assignment is Dermatitis Eksfoliatif Generalisata that is equal to 0.426 which show from the last calculation of Dempster-Shafer on symptom 5 which means the possibility of a temporary diseases with symptoms of blister, itch, scaly skin, fever, pain in the rash is the Dermatitis Eksfoliatif Generalisata.
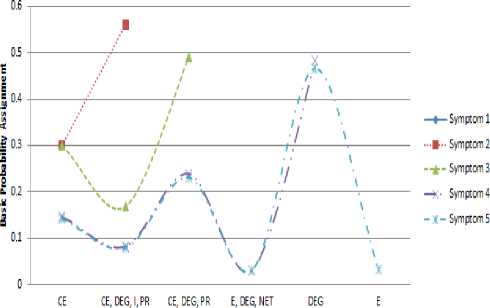
Diseases
Figure 6. Condition 5 (Dermatitis Eksfoliatif Generalisata as the highest basic probability assignment)
Figure 6 shows the graphic of Condition 5, we get the highest basic probability assignment is Dermatitis Ekfoliatif Generalisata that is equal to 0.466 which show from the last calculation of Dempster-Shafer on symptom 5 which means the possibility of a temporary diseases with symptoms of blister, itch, scaly skin, fever, pain in the rash is the Dermatitis Ekfoliatif Generalisata.
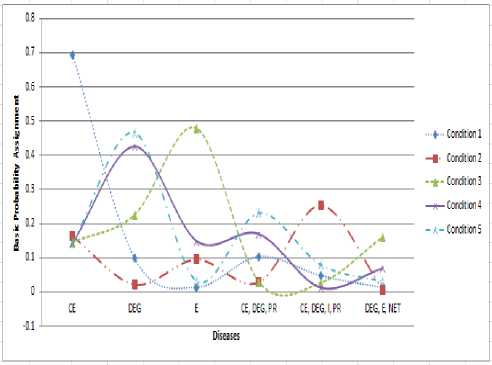
Figure 7. Final Result
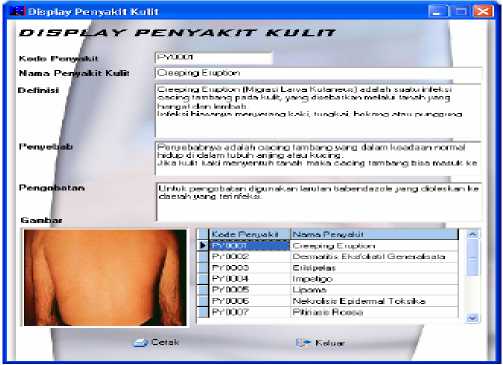
Figure 9. Consultation result
Figure 7 shows the highest basic probability assignment and the possibility of a temporary diseases for each condition. The highest bpa value for condition 1 is Creeping Eruption, condition 2 is skin diseases Creeping Eruption, Dermatitis Eksfoliatif Generalisata, Impetigo, and Pitriasis Rosea, condition 3 is Erisipelas, condition 4 is Dermatitis Eksfoliatif Generalisata, condition 5 is Dermatitis Ekfoliatif Generalisata. Condition 4 and condition 5 have similar basic probability assignment. Creeping Eruption in condition 1 needs serious treatment because has basic probability assignment more than 0.5.
III. IMPLEMENTATION
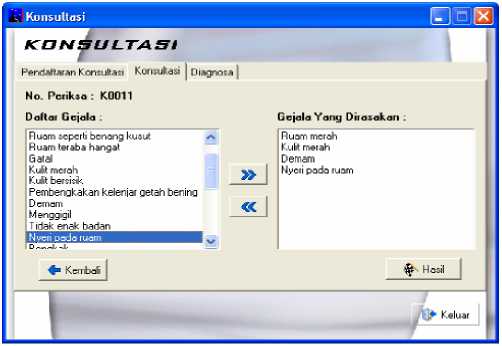
Figure 8. Symptom selection
In the case of blister, itch, scaly skin, fever, and pain in the rash, the result of consultation is creeping eruption with the density value 0.695. Figure 9 shows the result of consultation.
-
IV. CONCLUSION
Detection of skin diseases can be performed using Dempster-Shafer Theory. In this paper we describe five symptoms as major symptoms which include blister, itch, scaly skin, fever, and pain in the rash. Skin diseases which include dermatitis eksfoliatif generalisata, impetigo, pitriasis rosea, erisipelas, and nekrolisis epidermal toksika. The simplest possible method for using probabilities to quantify the uncertainty in a database is that of attaching a probability to every member of a relation, and to use these values to provide the probability that a particular value is the correct answer to a particular query. An expert in providing knowledge is uncertain in the form of rules with the possibility, the rules are probability value. The knowledge is uncertain in the collection of basic events can be directly used to draw conclusions in simple cases, however, in many cases the various events associated with each other. Reasoning under uncertainty that used some of mathematical expressions, gave them a different interpretation: each piece of evidence may support a subset containing several hypotheses. This is a generalization of the pure probabilistic framework in which every finding corresponds to a value of a variable. In this research, Dempster-Shafer theory has been successfully detecting skin diseases and displaying the result of identification process. This research can be an alternative in addition to direct consultation with the skin disease doctor and to find out quickly of skin diseases problems which can reduce serious economic and social consequences as well as health implications.
Список литературы Skin Diseases Expert System using Dempster-Shafer Theory
- R. Marks, A. Plunkett, K. Merlin, N. Jenner. Atlas of Common Skin Diseases in Australia. Department of Dermatology, St Vincent’s Hospital, Melbourne, Australia, 1999
- T. A. Grossbart, C. Sherman. Skin Deep. Health Press NA Inc., Albuquerque, New Mexico, 2009.
- H.A. Guvenir, N. Emeksiz. An expert system for the differential diagnosis of erythemato-squamous diseases. Expert Systems with Applications, v18, 2000, pp. 43–49.
- S. Karagiannis, A. I. Dounis, T. Chalastras, P. Tiropanis, and D. Papachristos. Design of Expert System for Search Allergy and Selection of the Skin Tests using CLIPS. World Academy of Science, Engineering and Technology v31, 2007, pp. 487-490.
- S.S.A. Naser, A.N. Akkila. A Proposed Expert System for Skin Infections Diagnosis. Journal of Applied Sciences Research, v 4, n12, 2008, pp. 1682-1693.
- A. P. Dempster. A Generalization of Bayesian inference. Journal of the Royal Statistical Society, 1968, pp. 205 – 247.
- G. Shafer. A Mathematical Theory of Evidence, Princeton University Press, New Jersey, 1976.
- J.A., Barnett. Computational methods for a mathematical theory of evidence. Proceedings of The 7th International Joint Conference on Artificial Intelligence, Vancouver, (1981), pp. 868-875.


