Скорость движения пассажиров в зависимости от плотности движения людей в часы пик работы метрополитена

• 1    Введение / Introduction

Во всем мире наблюдается тенденция к укрупнению городов и агломераций вследствие перетока людей в мегаполисы, связанного с повышением профессиональных возможностей, качества жизни и сформированной инфраструктурой. Рост населения мегаполисов сопровождается повышенной востребованностью жилищного строительства. Следовательно, в крупных российских городах наблюдается тенденция роста этажности (средняя этажность на данный момент – 17-18) и плотности жилой застройки, что приводит к необходимости увеличения количества и качества работы транспортных средств [1]–[3]. Недостаточное внимание к развитию городского транспорта в мегаполисах ведет к падению уровня качества жизни населения, что способствует падению экономической привлекательности агломерации [4]–[6]. Таким образом, одной из первостепенных задач транспортного планирования является развитие транспортной инфраструктуры в условиях стремительного роста и плотности населения и формирования мегаполисов.

Метрополитен относится к самому эффективному виду общественного транспорта с точки зрения перевозимого количества пассажиров, что обуславливает его применение в крупных агломерациях. Пропускная и провозная способности систем метрополитена определяются исходя из расчетного (для проектируемых метрополитенов) или существующего (для реконструируемых или действующих метрополитенов) пассажиропотока [7]. Пассажиропоток – однонаправленное или разнонаправленное движение пассажиров по обозначенной траектории, определяемое как количество пассажиров, проходящих за единицу времени через рассматриваемую топологию [8], [9]. Пассажиропоток определяет условия эксплуатации станции в утренний, вечерний «час пик» и при эксплуатационном режиме работы метрополитена (межпиковый период). Проектные решения метрополитена должны подвергаться анализу безопасного и комфортного нахождения пассажиров в зависимости от предполагаемого входного пассажиропотока, при резком увеличении которого действующие станции могут столкнуться с проблемой перенасыщения и с невозможностью управления движением людского потока.

К основным критериям выбора объемно-планировочных решений (ОПР) зданий и сооружений относятся безопасность, комфорт и экономическая эффективность [10]. В работе [11] разработана многокритериальная модель оценки качества транспортного обслуживания по результатам опроса пассажиров. Получено, что критерии комфорта, безопасности и социальной значимости являются наиболее важными для пассажиров. Безопасность нахождения пассажиров в метрополитене обуславливается следующими факторами [12]–[15]:

• –    регулирование увеличенного пассажиропотока;

• –    предотвращение повышенных скоплений людей на пассажирских топологиях станции с целью уменьшения травмоопасных ситуаций;

• –    предотвращение общественно-опасного поведения пассажиров;

• –    обеспечение своевременной и безопасной эвакуации в случае возникновения чрезвычайной ситуации, в том числе пожара;

• –    проектирование необходимых с точки зрения расчетного или существующего пассажиропотока размеров и количества вестибюлей, пандусов, дверей, турникетов, эскалаторов и платформ для обеспечения безопасного передвижения пассажиров.

Комфортные условия нахождения пассажиров в метрополитене обуславливаются следующими факторами [16]–[18]:

• –    создание благоприятной среды для пассажиров на всем пути их следования;

• –    поддержание оптимального уровень плотности людского потока на любой топологии;

• –    поддержание оптимального времени ожидания и длины очереди пассажиров перед средствами попутного обслуживания;

• –    обеспечение беспрепятственного движения основного потока пассажиров с минимальными временными затратами на ожидание в очереди;

• –    поддержание достаточного уровня освещенности, необходимого для быстрой ориентации пассажиров в метрополитене.

Имитационное моделирование позволяет проводить оценку принятых ОПР зданий и сооружений, определять будущее состояние системы на основе предыдущего состояния и отображать последовательность развития процессов внутри исследуемого объекта, а затем визуализировать поведение системы [19]–[21]. Например, работа [22] направлена на разработку имитационной модели эксплуатации кинотеатра, позволившая определить среднее время ожидания и длину очереди при различном количестве пешеходных потоков и билетных касс. В исследовании [23] проведено имитационное моделирование движения пассажиров в метрополитене с целью оценки формирования очереди перед билетными кассами и досмотровыми зонами и анализа ее влияния на движение основного потока пассажиров.

В транспортных системах существует большое количество независимых и параллельно действующих элементов, называемых агентами [24]. Использование агентного моделирования позволяет детально описывать движение агентов, выступающих в роли пассажиров. В работе [25] разработана агентная модель для визуализации работы транспортно-пересадочного узла и прогнозирования процесса пересадки между автобусной остановкой и железнодорожной пассажирской станцией. В результате работы предложен вариант организации общественного транспорта с целью уменьшения потери времени пассажиров. Исследование [26] направлено на выбор оптимального способа хранения, организации и доставки посылок с целью экономии затрат с использованием агентого моделирования. Получено, что система доставки всех посылок в конце недели является более эффективной с точки зрения минимизации затрат, тем не менее, Shabunina, D.; Kudryavtsev, V.; Chizhikov, V.

Passenger speeds as a function of human traffic density in peak hours of subway operation;

сверхбыстрая доставка пользуется большей популярностью из-за имеющейся высокой конкуренции. В работе [27] используется агентное моделирование движения людей по типовой станции метрополитена в эксплуатационном режиме и при эвакуации. Разработанная модель позволила определить «узкие» места, способные снизить уровень комфорта пассажиров при эксплуатационном режиме и ухудшить условия эвакуации. Таким образом, для детальной оценки функционирования транспортного объекта с точки зрения безопасности и комфорта пассажиров возможно применение агентного моделирования с точными исходными данными, описывающими характер движения агентов и особенность функционирования метрополитена.

Российский нормативный стандарт СП 120.13330.2022 «Метрополитены» [28] допускает для моделирования движения людей в эксплуатационном режиме использовать Приказ МЧС России № 1140, описывающий параметры движения людей различных групп мобильности на различных топологиях при эвакуации. Приказ МЧС России № 1140 приводит точную классификацию людских потоков и параметры их движения: подразделяет людей на группы без ограничения мобильности (М0 (Таблица 1)) и маломобильные группы населения (Таблица 2).

Таблица 1. Характеристики людей группы мобильности М0 в соответствии с Приказом МЧС России № 1140

Table 1. Characteristics of people in mobility group M0 in according to the Order of the Ministry of Emergency Situations of Russia No. 1140

	Группа мобильности	Пропускная способность, чел./ч
Однородные группы	М0-1	Дети и подростки (7-18 лет)
	М0-2	Молодежь (18-25 лет)
	М0-3	Люди трудоспособного возраста (18-60 лет)
Неоднородные группы	М0-4	Группа, состоящая из детей дошкольного и школьного возраста и людей трудоспособного возраста
	М0-5	Группа, состоящая из детей дошкольного и школьного возраста, людей трудоспособного возраста и активных людей пожилого возраста
	М0-6	Группа, состоящая из людей трудоспособного возраста и активных людей пожилого возраста
	М0-7	Группа, состоящая из людей с грудными детьми, детей дошкольного и школьного возраста, людей трудоспособного возраста, активных людей пожилого возраста

Таблица 2. Характеристики маломобильных групп населения в соответствии с Приказом МЧС России № 1140

Table 2. Characteristics of disabled people in according to the Order of the Ministry of Emergency Situations of Russia No. 1140

Группа мобильности	Пропускная способность, чел./ч
М1	Люди, не имеющие инвалидности, со сниженной мобильностью, глухие и слабослышащие
М2	Пожилые немощные люди, слепые и слабовидящие люди
М3	Люди трудоспособного возраста с поражением опорно-двигательного аппарата
М4	Инвалиды, передвигающиеся на креслах-колясках
НМ	Немобильные граждане
НТ	Нетранспортабельные люди
НО	Люди с ограниченной степенью свободы, в том числе люди с психическими отклонениями

Приказ МЧС России № 1140 приводит соотношение эвакуируемого контингента по группам мобильности в зависимости от класса функциональной пожарной опасности здания и минимальное расчетное количество людей в здании в момент начала эвакуации, при этом данные для метрополитена отсутствуют.

Скорость движения людского потока зависит от плотности их движения, вида пути, состава группы мобильности и от общего психологического состояния группы людей. В учебном пособии Холщевникова В. В., Самошина Д. А., Парфененко А. П., Кудрина И. С., Истратова Р. Н., Белосохова И. Р «Эвакуация и поведение людей при пожарах» приведено, что на двигательную активность влияет уровень эмоционального состояния (Таблица 3).

Таблица 3. Скорости движения людей в потоке при различных категориях движения Table 3. Speeds of movement of people in the flow at different traffic categories

Категории движения	Скорость свободного движения V 0 по видам пути, м/мин
	Горизонтальный участок, лестница вниз	Лестница вверх
Комфортное	< 49.0	< 27.0
Спокойное	49.0-66.0	27.0-38.0
Активное	66.0-90.0	38.0-55.0
Повышенной активности	90.0-120.0	55.0-75.0

Приказ МЧС России № 1140 приводит зависимости скоростей свободного движения людей от плотности людского потока при эвакуации. Процесс эвакуации вследствие возникновения пожара или иной чрезвычайной ситуации относится к категории движения пассажиров «повышенная активность», а движение пассажиров при эксплуатационном режиме работы метрополитена – к спокойному или активному типу движения (Таблица 3). Тем самым, применение Приказа МЧС России № 1140 при моделировании эксплуатационного режима работы для анализа влияния принятых ОПР метрополитена невозможно по ряду следующих причин:

• –    происходит завышение скоростей движения пассажиров, что приводит к принятию недостаточного количества основных элементов станций;

• –    отсутствуют данные или зависимости по определению количества людей на пассажирских топологиях станции метрополитена в любой момент времени;

• –    отсутствуют данные по соотношению групп мобильности в метрополитене.

Целью работы является получение зависимостей скоростей движения пассажиров различных групп мобильности от плотности людского потока при эксплуатационном режиме работы метрополитена.

Для достижения цели решены следующие задачи: проведены экспериментальные исследования по наблюдениям в часы пиковой загруженности за скоростями движения пассажиров на загруженных станциях Петербургского метрополитена, составлен алгоритм обработки экспериментальных данных, по которому получены зависимости скоростей движения пассажиров от плотности людского потока, проведено сравнение экспериментальных данных по скоростям движения пассажиров со скоростями, приведенными в Приказе МЧС России № 1140.

• 2 Материалы и методы / Materials and Methods

2.1    Экспериментальные исследования движения пассажиров / Experimental studies of passenger traffic

Экспериментальные исследования включают в себя наблюдение с камер видеонаблюдения метрополитена и переносных камер на штативе за скоростями движения пассажиров на различных топологиях от плотности людского потока.

Для определения скоростей движения пассажиров проведены экспериментальные исследования на загруженных станциях Петербургского метрополитена: «Площадь Восстания», «Проспект Ветеранов», «Проспект Просвещения», «Московская», «Садовая» и «Сенная площадь» (Рисунок 1,2).

Рис. 1 - Горизонтальные пути движения на станциях «Московская» и «Проспект Просвещения»

Fig. 1 - Horizontal sites of traffic at the stations «Moskovskaya» and «Prospekt Prosveshcheniya»

Рис. 2 - Лестничные сходы на станциях «Садовая» и «Сенная площадь»

Fig. 2 - Stairways at the stations «Sadovaya» and «Sennaya Ploshchad»

Для определения трека перемещения и скорости движения в потоке строилась кинограмма движения i - ого человека, в которой графически фиксировались его перемещения. На основании данных видеонаблюдения подсчитывалось общее количество людей N_n^t , попавших в каждую клетку n расчетной сетки, и их принадлежности к группам мобильности. Общая плотность каждой отдельной клетки n вычисляется по формуле (1):

t N n ^t n F

где N_n^t – количество людей в расчетной клетке, чел.; F_n – площадь расчетной клетки, м².

Из общего потока выбирался человек, за движением которого велось наблюдение. Определялось количество людей N_n + △ t в ячейке расчетной сетки, в которой находился наблюдаемый человек в момент времени t + △ t . Значение плотности потока, при которой происходило движение i - ого человека внутри расчетной клетки, определялось по формуле (2):

D t =

N>N r

2 ■ F n

•

Скорость движения

i - ого человека по траектории его движения на интервале ( t , t + △ )

определялась формулой (3):

V ( t , t + △ t ) = △ l

i            △t ’ где △ t - интервал времени, за который пассажир преодолевает расстояние △ l, с.

Данные вычисления повторяются для i - ого человека до его выхода из зоны наблюдения либо до прохождения им заданного сечения пути.

2.2    Обработка экспериментальных исследований / Processing of experimental studies

При обработке экспериментальных данных использовался метод наименьших квадратов, позволяющий построить оптимальную оценку моментов распределения ошибки эксперимента [29–31]. В общем случае предполагается, что между независимыми переменными и результатом процесса существует функциональная связь, описываемая уравнением (4):

y = y ( x ) ,

где x = ( x 1 , x ₂, . , x n ) ' - вектор значений независимых переменных. Значения x_i представлены в безразмерном виде в виде уравнения (5):

D -0.5 (D + D } i * max min

0.5 • {D - D . ) * max min где Di - действительное значение плотности людского потока; Dmax, Dmin - максимальное и минимальное значение переменной плотности людского потока.

При обработке результатов экспериментальных исследований принята полиномиальная модель второго порядка линейная относительно коэффициентов a i вида (формула (6)):

y ( a , ^x ) = a 0 • f 0 ( ^x ) + a ! • f ( ^x ) + ... + a k • f_k ( ^x ) .

Исходными данными при определении значений коэффициентов a i являются: – матрица, описываемая уравнением (7):

F = ( f k ( xN ) ) =

f > ( x 1)    f l ( x 1)    .    f k ( x 1) f > ( x )    f ( x )   •••    fk ( x )  .                                 (7) f > ( x N )   f 1 ( x N )   .   fk ( x N )

– вектор результатов наблюдений, описываемый уравнением (8):

FY = ( у1, у2,..., y N)'.

Расчет коэффициентов производится из условия обеспечения минимального значения расширенной квадратичной формы согласно уравнению (9):

S = ( y ‘ — yi)2 =' Y — Y |2 = (Y — Y )' (Y — Y) *

Оценка дисперсии наблюдений вычисляется с помощью суммы квадратов ошибок (формула (10)) с числом степеней свободы ^ ₂ (формула (11)) по формуле (12):

N у

Se =ЕХ(уj- y^2, i=1 j =1

^2 = N •( 7 -!),

S s = ——,

7^ 2

где N - количество опытов: у - количество опытов в одной точке; y^ij - результат наблюдений в точке; y i - среднее значение результата наблюдений в точке.

Сумма квадратов рассчитывается по формуле (13) и имеет ^ = N - к - 1 степеней свободы.

N ₂

S d = Y / ( y -Я .

i = 1

Величина F – критерия, характеризующего адекватность модели, определяется из (14):

F = ^SD / ^ 1

S e / ^ 2

.

Доверительный интервал для коэффициентов с вероятностью P определяется из (15):

| ai - ai | < si ’ £, где г - табличное значение коэффициента, определяемого из условия (16):

P(X < г) = 1 - a.

a ˆ _i – вектор коэффициентов модели, определяемый по формуле (17):

F' - транспонированная матрица F ; Y - вектор результатов наблюдений.

Проверка значимости коэффициентов модели производится из условия (18):

aˆ i

> t kp • s i ,

где t_кр – критическое значение распределения Стьюдента для заданного уровня значимости.

Критерии выбора точек для статистической обработки:

• –    количество измеренных значений в одной точке – не менее двух;

• –    исключение точек, имеющих максимальное отклонение от начальной линии тренда;

• –    в качестве линии тренда принимается полином второй степени.

3.1 Зависимости движения пассажиров группы мобильности М0-3

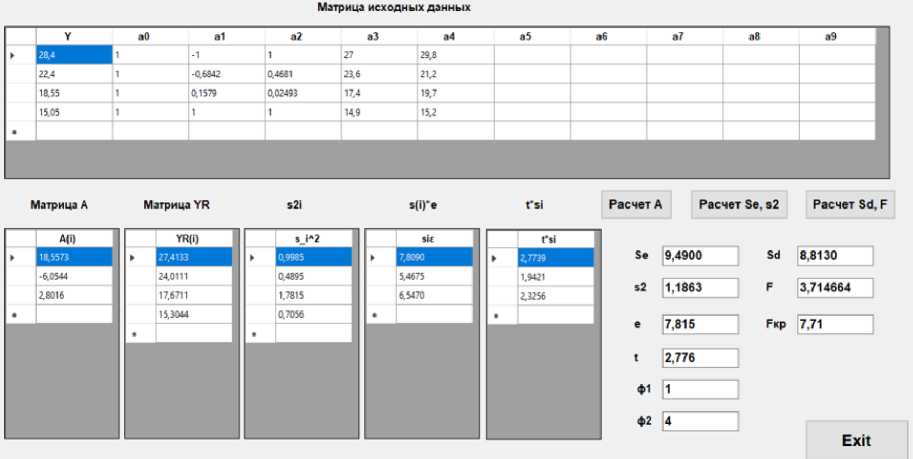
Для реализации методики обработки экспериментальных значений разработана программа, в которую вошли математические зависимости (4)-(18) для автоматизации процесса.

3 Результаты и обсуждение / Results and Discussion

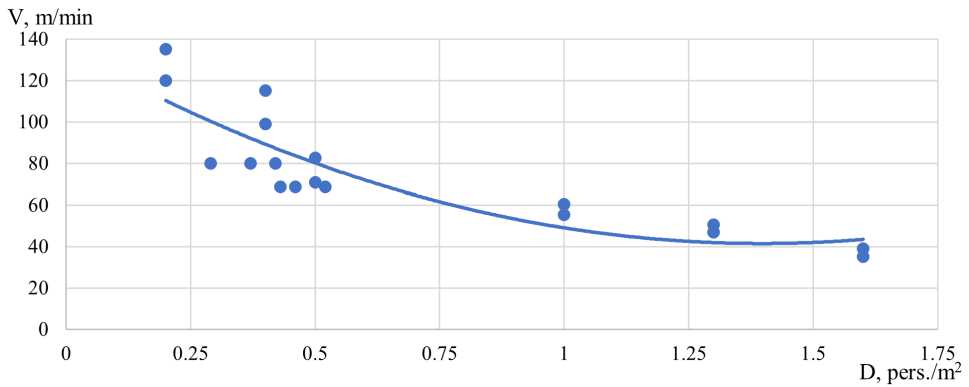
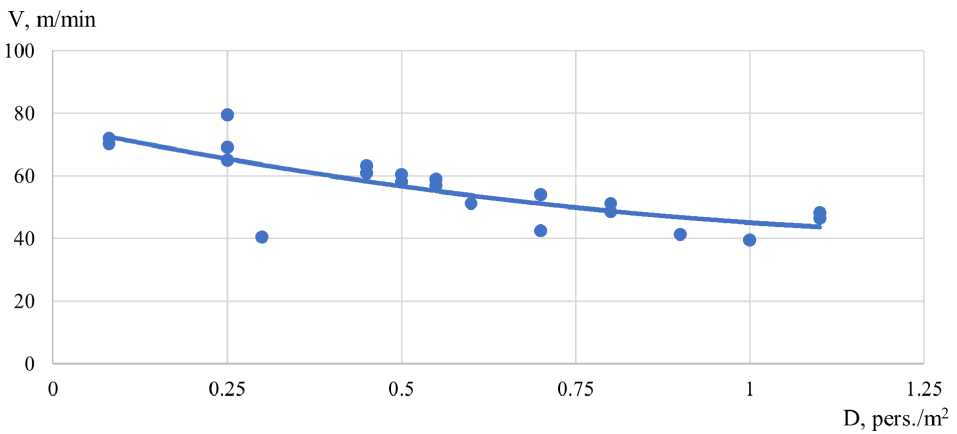
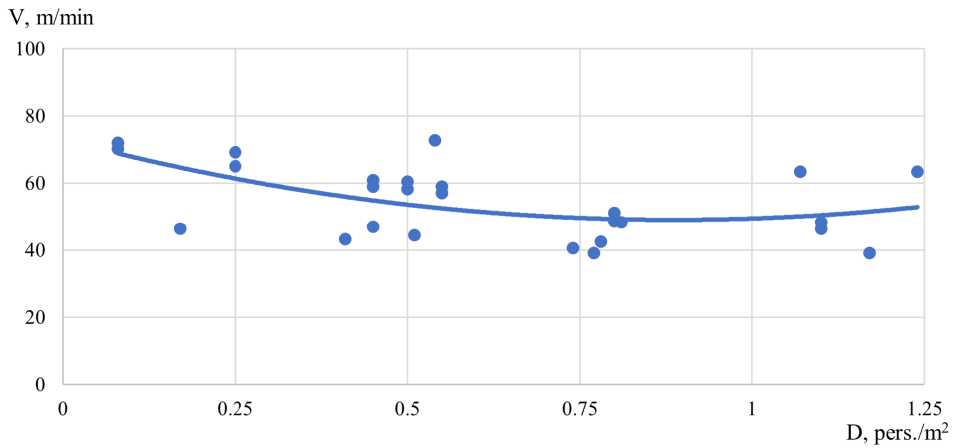
Наблюдение за движением пассажиров группы мобильности М0-3 приведены на рисунке 3.

а)

б)

в)

Рис. 3 - Зависимость движения пассажиров группы мобильности М0-3: а) по горизонтальному участку; б) по лестнице вниз; в) по лестнице вверх

Fig. 3 - Dependence of passenger movement of mobility group M0-3: a) on the horizontal site; b) on the downward staircase; c) on the upward staircase

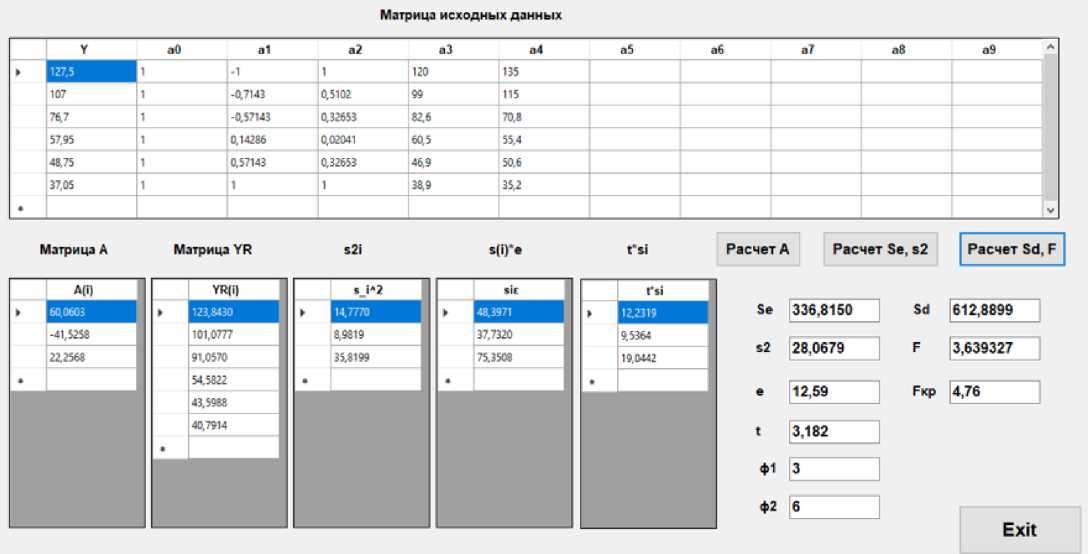
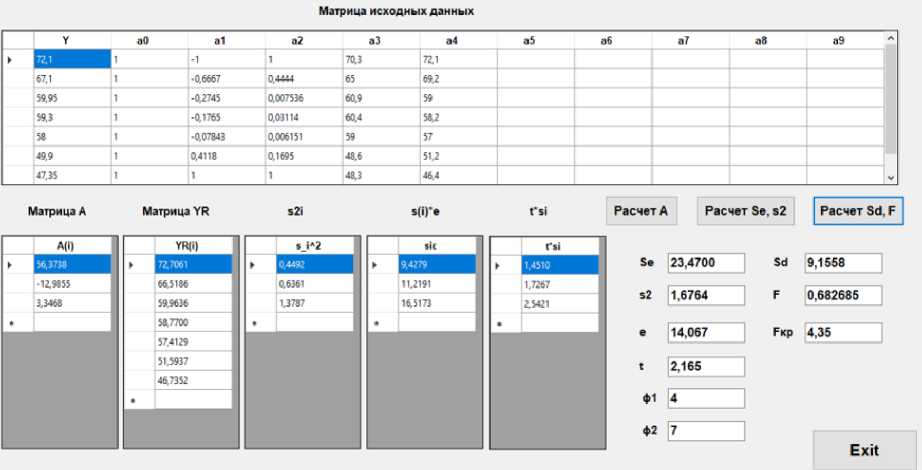
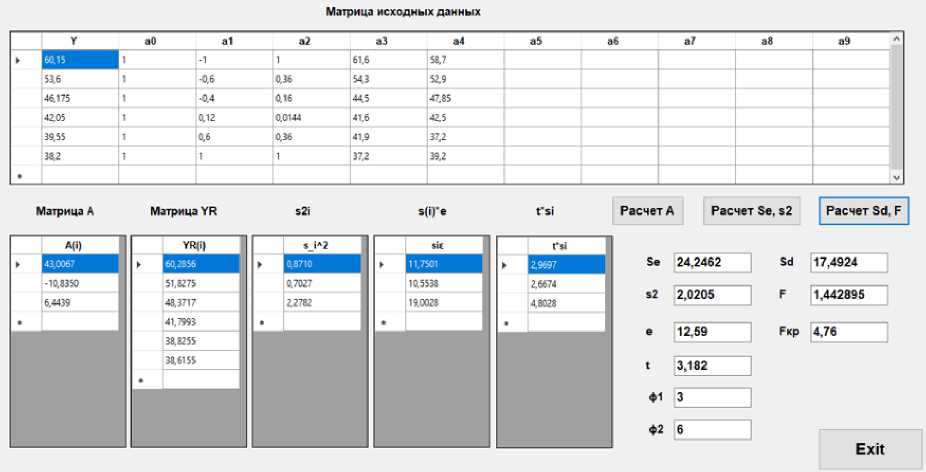
Результаты расчетов представлены на рисунке 4.

а)

б)

в)

Рис. 4 - Результаты расчета движения пассажиров группы мобильности М0-3: а) по горизонтальному участку: б) по лестнице вниз; в) по лестнице вверх

Fig. 4 - Results of calculation of passenger movement of mobility group M0-3: a) on the horizontal site: b) on the downward staircase; c) on the upward staircase

Получены полиномиальные модели второго порядка (19)-(21).

y = 60.06 - 41.53 • x + 22.26 • x ²,                                  (19)

y = 56.37 - 12.98 • x + 3.35 • x ²,                                     (20)

y = 43.01 - 10.84 • x + 6.44 • x ²,

где y – скорость движения пассажиров М0-3 по горизонтальному участку, лестнице вниз и лестнице вверх соответственно, м/мин; x – плотность потока на горизонтальном участке, лестничном сходе (спуск), лестничном сходе (подъем) соответственно в безразмерном виде.

Условия F = 3.639 <  F_kp = 4.76, F = 0.683 <  F_kp = 4.35, F = 1.44 <  F_kp = 4.76, следовательно, модели являются адекватными (рисунок 4).

Скорости движения пассажиров группы мобильности М0-3 как функция от плотности людского потока определяются зависимостями (22)-(24).

v = 150.24 - 141.08 • D + 45.422 • D 2 ,

v = 75.875 - 40.645 • D +12.867 • D2, v = 70.806 - 57.756 • D + 25.776 • D2, где v – скорость движения пассажиров группы мобильности М0-3 по горизонтальному участку, лестнице вниз и лестнице вверх соответственно, м/мин; D – плотность людского потока, чел/м2.

3.2    Зависимости движения пассажиров группы мобильности М2

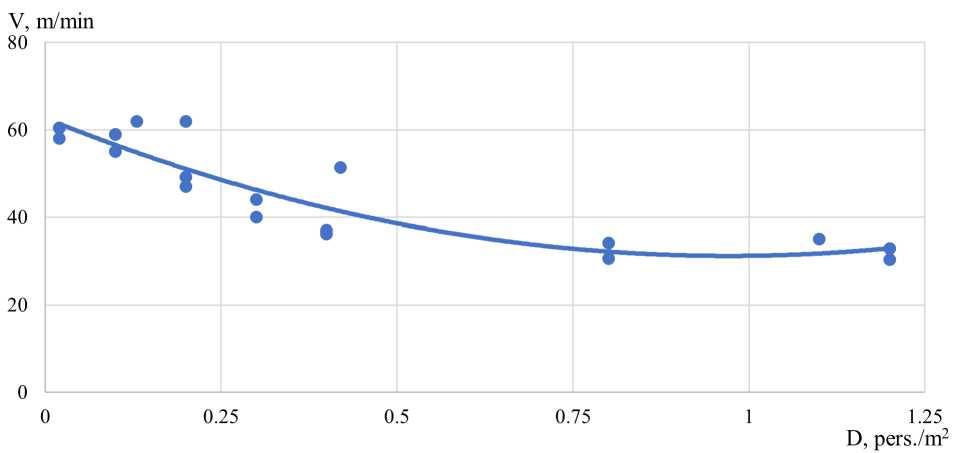
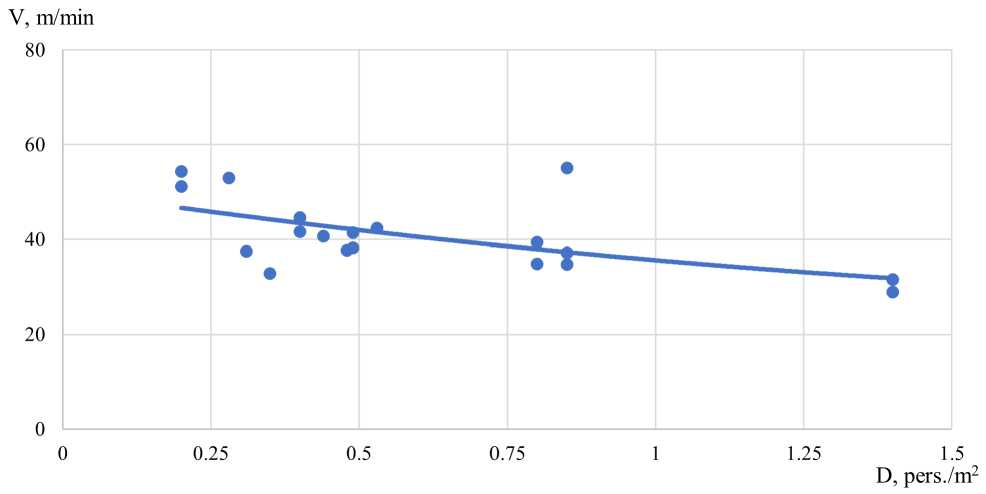
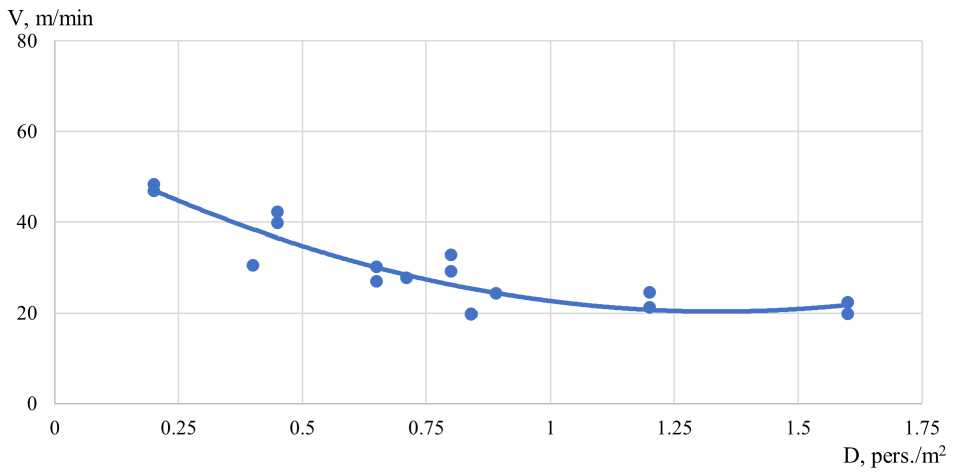
Наблюдение за движением пассажиров группы мобильности М2 приведены на рисунке 5.

а)

б)

в)

Рис. 5 - Зависимость движения пассажиров группы мобильности М2: а) по горизонтальному участку: б) по лестнице вниз; в) по лестнице вверх

Fig. 5 - Dependence of passenger movement of mobility group M2: a) on the horizontal site: b) on the downward staircase; c) on the upward staircase

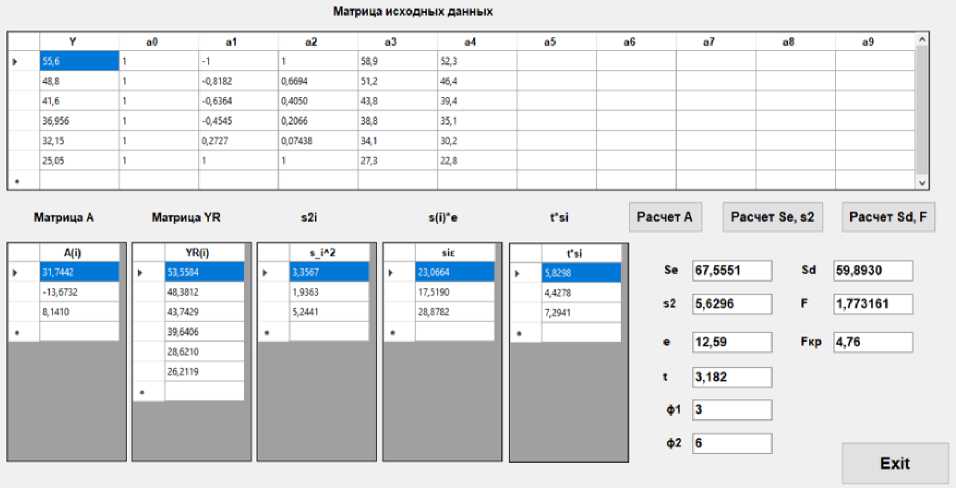
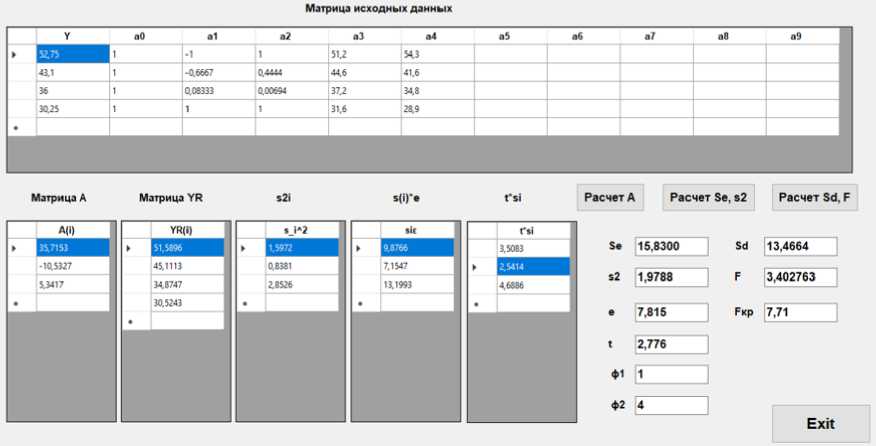
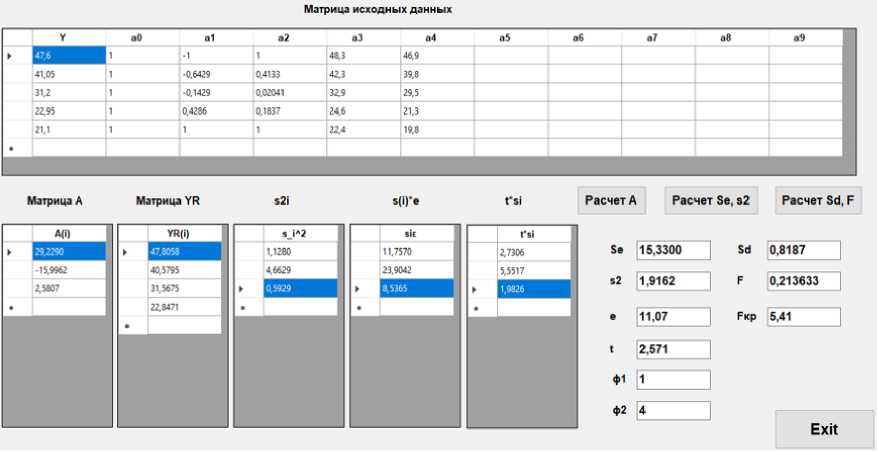
Результаты расчетов приведены на рисунке 6.

а)

б)

в)

Рис. 6 - Результаты расчета движения пассажиров группы мобильности М2: а) по горизонтальному участку: б) по лестнице вниз; в) по лестнице вверх

Fig. 6 - Results of calculation of passenger movement of mobility group M2: a) on the horizontal site: b) on the downward staircase; c) on the upward staircase

Получены полиномиальные модели второго порядка (25)-(27).

y = 31.74 - 13.67 ■ x + 8.14 • x 2 ,                                     (25)

y = 35.72 - 10.53 ■ x + 5.34 ■ x 2 ,

y = 29.23 -16.00 • x + 2.58 • x2, где y – скорость движения пассажиров М2 по горизонтальному участку, лестнице вниз и лестнице вверх соответственно, м/мин; x – плотность потока на горизонтальном участке, лестничном сходе (спуск), лестничном сходе (подъем) соответственно в безразмерном виде.

Условия F = 1.77 <  F_Kp = 4.76, F = 3.40 <  F_Kp = 7.71, F = 0.21 <  F_kp = 5.41, следовательно, модели являются адекватными (рисунок 6).

Скорости движения пассажиров группы мобильности М2 как функция от плотности людского потока определяются зависимостями (28)-(30).

v = 59.273 - 59.842 • D + 26.909 • D2, v = 59.255 - 41.295 • D +14.838 • D2, v = 54.062 - 32.332 • D + 5.267 • D2,

где v – скорость движения пассажиров группы мобильности М2 по горизонтальному участку, лестнице вниз и лестнице вверх соответственно, м/мин; D – плотность людского потока, чел/м².

3.3.    Зависимости движения пассажиров группы мобильности М3

Наблюдение за движением пассажиров группы мобильности М3 приведены на рисунке 7.

0.25

0.75

1.25

1.5

D, pers./m2

б)

а)

V, m/min

в)

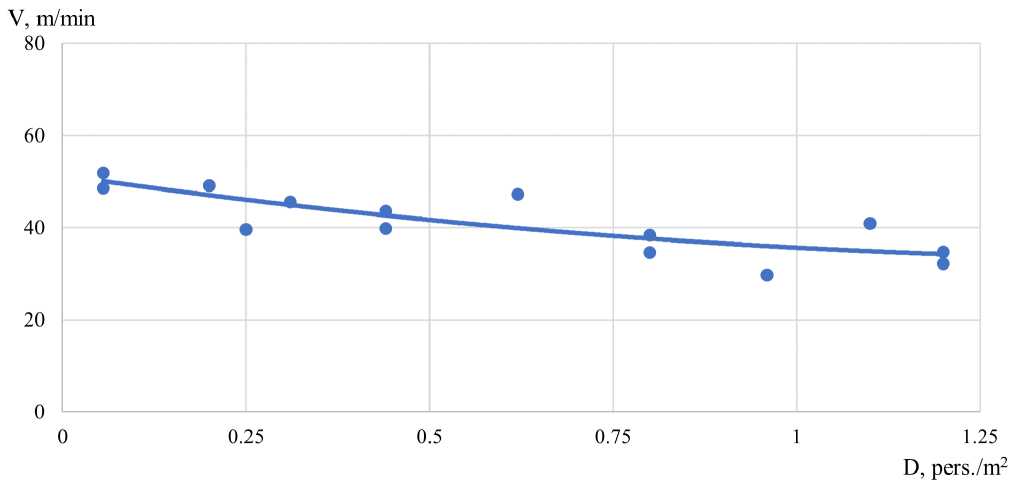
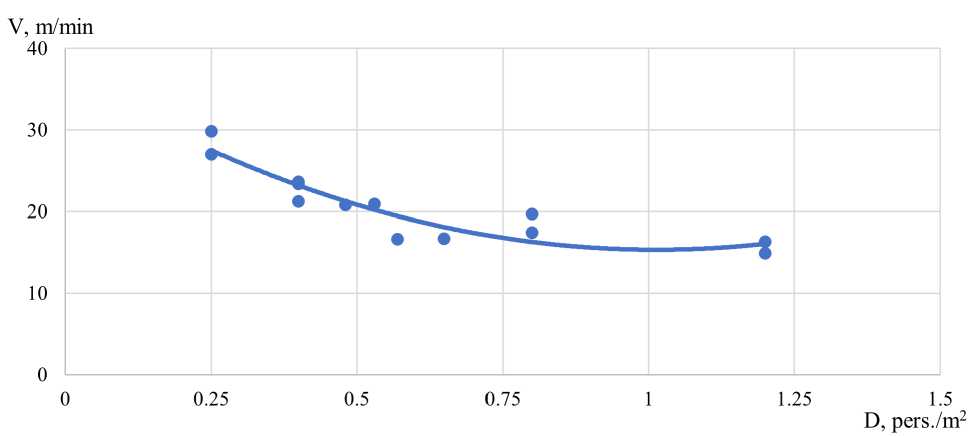
Рис. 7 - Зависимость движения пассажиров группы мобильности М3: а) по горизонтальному участку: б) по лестнице вниз; в) по лестнице вверх

Fig. 7 - Dependence of passenger movement of mobility group M3: a) on the horizontal site: b) on the downward staircase; c) on the upward staircase

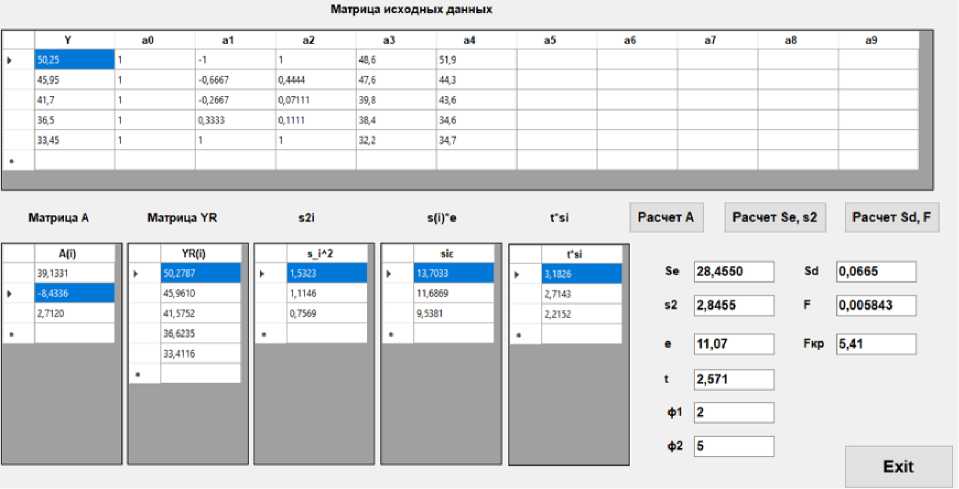
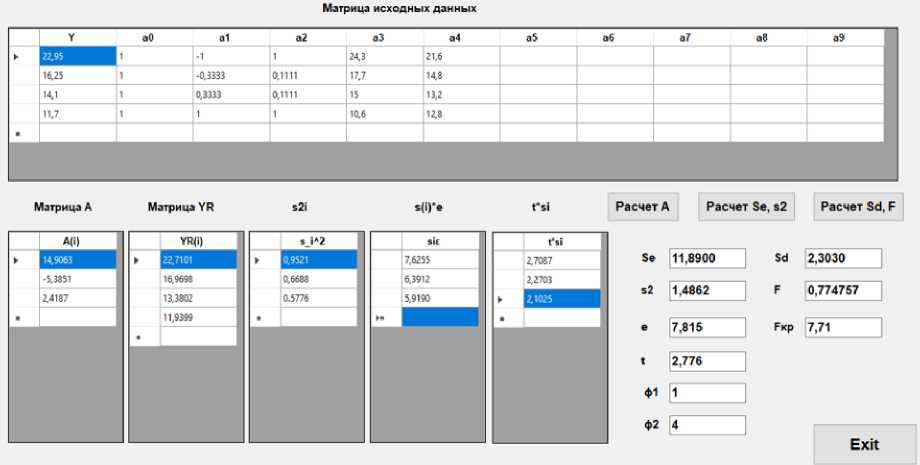
Результаты расчетов приведены на рисунке 8.

а)

б)

в)

Рис. 8 - Результаты расчета движения пассажиров группы мобильности М3: а) по горизонтальному участку: б) по лестнице вниз; в) по лестнице вверх

Fig. 8 - Results of calculation of passenger movement of mobility group M3: a) on the horizontal site: b) on the downward staircase; c) on the upward staircase

Получены полиномиальные модели второго порядка (31)-(33).

y = 39.13 - 8.43 • x + 2.71 - x ²,                                     (31)

y = 14.91 - 5.39 • x + 2.42 • x ²,                                     (32)

y = 18.56 - 6.05 • x + 2.80 • x ²,

где y – скорость движения пассажиров М3 по горизонтальному участку, лестнице вниз и лестнице вверх соответственно, м/мин; x – плотность потока на горизонтальном участке, лестничном сходе (спуск), лестничном сходе (подъем) соответственно в безразмерном виде.

Условия F = 0.006 <  F_kp = 5.41, F = 0.775 <  F_kp = 7.71, F = 3.71 <  F_kp = 7.71, следовательно, модели являются адекватными (рисунок 8).

Скорости движения пассажиров группы мобильности М3 как функция от плотности людского потока определяются зависимостями (34)-(36).

v = 50.279 - 23.096 • D + 7.533 • D2, v = 26.386 -19.725 • D + 6.719 • D2, v = 34.325 - 30.75 b D +12.417 • D2, где v – скорость движения пассажиров группы мобильности М3 по горизонтальному участку, лестнице вниз и лестнице вверх соответственно, м/мин; D – плотность людского потока, чел/м2.

3.3    Обсуждение / Discussion

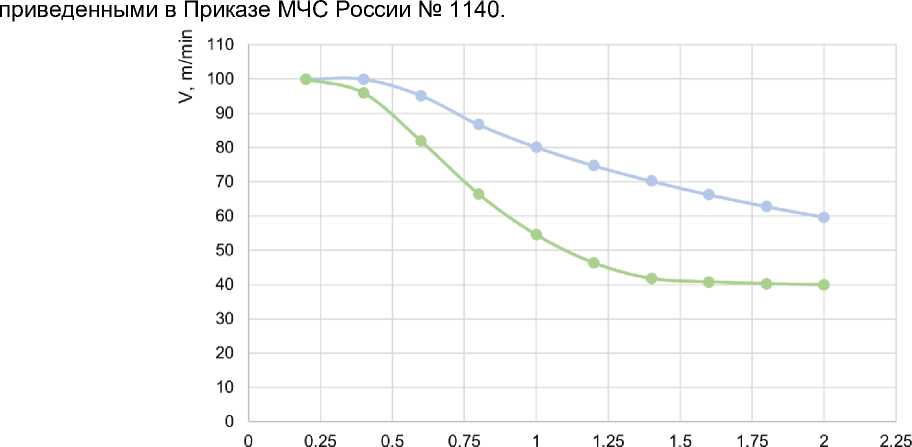
По результатам экспериментальных исследований проведена оценка соотношения групп мобильности пассажиров и получено, что количество людей группы мобильности М2 и М3 на пассажирских топологиях метрополитена составляет 0,62% от общего входного и выходного пассажиропотоков. На рисунке 9 представлено сравнение полученных экспериментальных данных по скоростям движения пассажиров группы мобильности М0-3 со скоростями,

Приказ МЧС России № 1140 —•—Экспериментальное исследование О, pers./m2

б)

в)

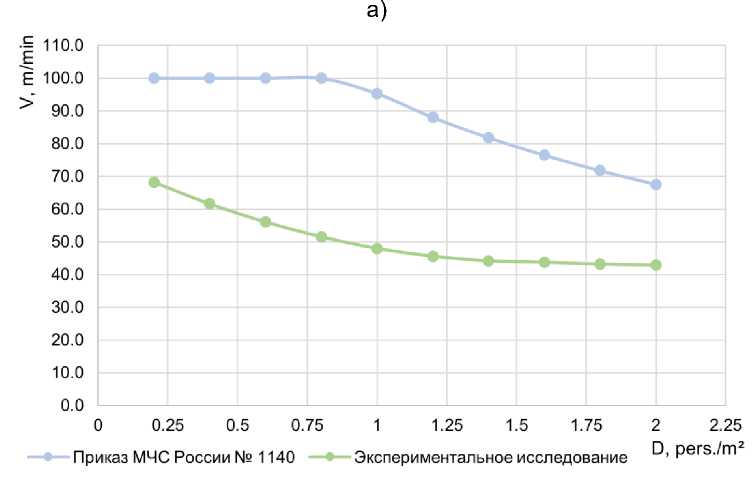
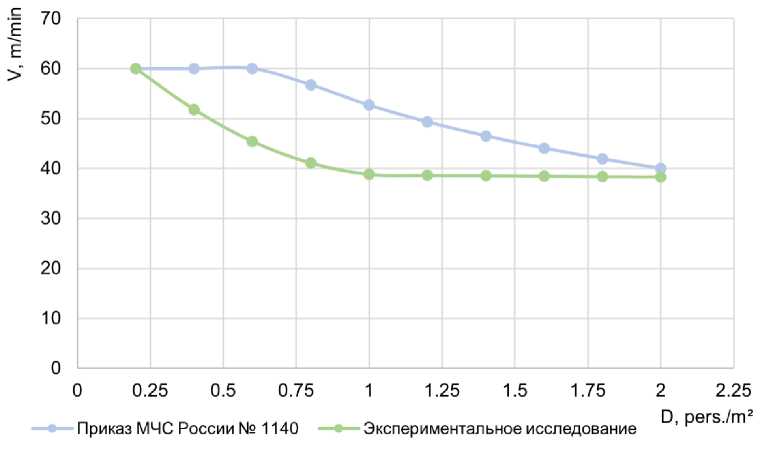
Рис. 9 - Сравнение экспериментальных скоростей движения пассажиров группы мобильности М0-3 со скоростями, приведенными в Приказе МЧС России № 1140 при движении по: а) горизонтальному участку: б) лестнице вниз; в) лестнице вверх

Fig. 9 - Comparison of experimental speeds of passengers of mobility group M0-3 with the speeds given in the Order of the Ministry of Emergency Situations of Russia No. 1140 on: a) horizontal site: b) the downward staircase; c) the upward staircase

Как видно из рисунка 9, скорость движения пассажиров по горизонтальному пути, при спуске и подъеме по лестничному сходу снижается при увеличении плотности людского потока. Согласно экспериментальному исследованию, при достижении плотности потока 1.5 чел./м2 на горизонтальном участке скорость движения остается постоянной (40 м/мин); при достижении плотности потока 1.5 чел./м2 при спуске на лестничном сходе скорость движения остается постоянной (43 м/мин); при достижении плотности потока 1.0 чел./м2 при подъеме на лестничном сходе скорость движения остается постоянной (38 м/мин).

Значения скоростей, приведенные в Приказе МЧС России № 1140, в среднем завышены: на 75% по горизонтальному пути движения, на 20% при спуске на лестничном сходе, на 40% при подъеме на лестничном сходе по сравнению со скоростями, полученными по экспериментальному исследованию (рисунок 9). Данное расхождение связано с тем, что Приказ МЧС России № 1140 учитывает тип движения пассажиров при эвакуации, который относится к категории движения пассажиров «повышенная активность», а движение пассажиров при эксплуатационном режиме работы метрополитена – к спокойному или активному типу движения.

• 4 Заключение / Conclusions

К основным критериям формирования ОПР станций метрополитена относятся безопасность и комфорт пассажиров. Моделирование эксплуатационного режима работы метрополитена практически важно для принятия оптимальных ОПР, обеспечивающих непрерывное функционирование станции. По результатам проведения экспериментальных исследований:

• 1.    Получены зависимости скоростей движения пассажиров группы мобильности М0-3, М2 и М3 от плотности людского потока;

• 2.    Получены максимальные значения плотностей людских потоков, при которых скорости движения пассажиров остаются постоянными;

• 3.    Проведено сравнение экспериментальных данных по скоростям движения пассажиров различных групп мобильности со значениями скоростей, приведенных в Приказе МЧС России № 1140.

• 4.    Определен средний процент нахождения маломобильных групп населения в метрополитене в часы пиковой загруженности станции (утренний и вечерний «час пик») – 0,62% от общего входного и выходного пассажиропотоков.

На основании полученных зависимостей скоростей движения пассажиров группы мобильности М0-3, М2 и М3 от плотности людского потока сделаны следующие выводы:

• 1.    При увеличении плотности людского потока уменьшается скорость движения пассажиров по горизонтальному пути, при спуске и подъеме по лестничному сходу.

• 2.    При достижении максимальных значений плотностей людских потоков значение скоростей движения пассажиров остаются постоянными: на горизонтальном участке скорость движения принимается 40 м/мин при плотности, большей 1.5 чел./м²; при спуске на лестничном сходе скорость движения принимается 43 м/мин при плотности, большей 1.5 чел./м²; при подъеме на лестничном сходе скорость движения принимается 38 м/мин при плотности, большей 1.0 чел./м².

• 3.    Применение скоростей, приведенных в Приказе МЧС России № 1140, недопустимо при моделировании эксплуатационного режима работы метрополитена по причине учета другого типа движения пассажиров (процесс эвакуации).

Полученные зависимости скоростей движения пассажиров группы мобильности М0-3, М2 и М3 от плотности людского потока могут использоваться в качестве исходных данных при разработке агентной модели движения пассажиров для решения следующих практических задач:

• -    Определение достаточности принятых ОПР метрополитена с точки зрения комфортного и безопасного нахождения пассажиров (моделирование эксплуатационного режима);

• -    Получение расчетной численности пассажиров, эвакуирующихся со станции при пожаре (получение исходных данных по количеству находящихся на пассажирских топологиях людей в момент начала эвакуации).