Скорость и распределение скорости метеороидов и частиц космического мусора в околоземном космическом пространстве

Для определения степени ущерба, наносимого космическому аппарату (КА) при встрече с высокоскоростными частицами метеороидов и/или техногенных частиц космического мусора (КМ), необходимо знать их массу и скорость. Скорость частиц используется в баллистических предельных уравнениях (БПУ) [1] как один из определяющих параметров для определения критического размера (массы) частиц, наносящих повреждение. Знание скорости метеороидов также используется при построении моделей метеороидной среды [2]. В частности, при обработке данных, полученных по методу прямых измерений (in situ measurements — экспонирование пластин и ловушек в космическом пространстве) с целью определения плотности потока частиц метеороидов и их массового распределения, важную роль играет величина их скорости [3]. Знание внеатмосферной скорости метеороидов также используется при изучении процессов свечения метеоров и свойств атмосферы.

Сумма скоростей метеороидов относительно Земли ( U — геоцентрическая скорость) и Земли относительно Солнца ( W — орбитальная скорость Земли) равна скорости метеороидов относительно Солнца ( V — гелиоцентрическая скорость метеороидов) — рис. 1.

Земля движется со скоростью W = 29,8 км/с. Гелиоцентрическая скорость метеороида V на среднем расстоянии Земли от Солнца (1 а. е.) не превышает 42,2 км/с (параболическая или третья космическая скорость [4]). Если метеороид догоняет Землю, то подлетает к ней со скоростью U = 42,2 – 29,8 = 12,4 км/с.

В случае, когда Земля встречает метеороид «в лоб», возможная его максимальная скорость U = 29,8 + 42,2 = 72 км/с. Если наблюдается большая скорость, то это указывает на гиперболическое движение метеорного тела относительно Солнца и, следовательно, на прилёт его из межзвёздного пространства.

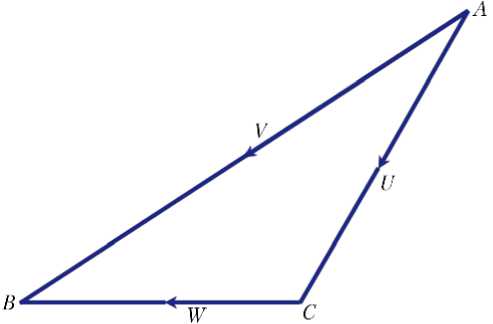
Рис. 1. Гелиоцентрическая (V) и геоцентрическая (U) скорости метеороидов; W — скорость Земли на орбите

(U = V - W )

В предположении, что все направления движения метеороидов в окрестности Земли равновероятны, а их гелиоцентрическая скорость фиксирована (~40 км/с), легко показать, что число догоняющих метеороидов должно быть меньше числа встречных. В действительности оказалось, что большинство метеороидов догоняют Землю, а не движутся ей навстречу. Причину этого удалось выяснить после определения различными методами направлений движения (орбит) и скорости отдельных метеоров (спорадических метеороидов, вошедших в атмосферу Земли) и метеорных потоков. Оказалось, что преимущественное направление движения метеороидов совпадает с направлением вращения Земли вокруг Солнца. Их орбиты представляют собой эллипсы, период обращения вокруг Солнца составляет от 0,5 до 10 лет. При этом орбиты, включая и сильно наклонённые к эклиптике, распределены в пространстве приблизительно равномерно [4]. Скорости основных метеорных потоков приведены в табл. 1

Согласно данным о метеороидах самых мелких размеров, среди них выделяют шесть характерных популяций [5, 6]:

• •    внутренние ( Core population );

• •    астероидные ( Asteroidal population );

• •    гало-метеороиды ( Halo population );

• •    метеороиды с большим наклонением орбиты ( Inclined population / i -метеороиды);

• •    эксцентриситетные ( Eccentric population / e -метеороиды);

• •    межзвёздная пыль ( Inter-Stellar Dust ( ISD ) population ).

Таблица 1

главные метеорные потоки (ливневые) и их скорости V_E относительно земли

Главные метеорные потоки	VE , км/с
Квандратиды/Лириды	41,5/47,6
П -Аквариды/Ориониды	65,5/66,4
Ариэтиды */С-Персеиды*	37/41
Р-Тауриды*	28,0–32,2
Персеиды — Комета 1862 III	59,4
Дракониды — Комета Джакобини-Циннера	22,0–20,4
Андромедиды — Комета Биелы	16,5–18,0
Леониды — Комета Темпеля-Туттля	70,7–70,8
Геминиды	34,4
Урсиды — Комета Туттля	33,4–34,5

Примечание. * — дневные потоки, наблюдаемые исключительно радиолокационными методами.

Кроме этого, в настоящее время полагается, что фон спорадических метеороидов в окрестностях Земли обусловлен шестью основными источниками: I — солнечным ( hellion ); II — антисол-нечным ( anti-hellion ); III — Северным тороидальным ( North toroidal ); IV — Южным тороидальным ( South toroidal ); V — северного апекса ( North Apex ) и VI — южного апекса ( South Apex ).

На рис. 2 приведена схема расположения источников (точек исхода) спорадических метеороидов на небесной сфере [6].

Компоненты северного и южного апексов, что понятно из названия, сосредоточены на направлении движения Земли. Северный и Южный тороидальные источники метеороидов сосредоточены приблизительно на 60 ° выше и ниже эклиптики и в направлении движения Земли [7].

Каждый источник метеороидов имеет популяцию частиц с его собственным распределением орбитальных характеристик, в т. ч., естественно, и скорости метеороидов. Первоначально относительная численность метеороидов от этих источников была оценена Брауном ( Brown ) и Джоунсом ( Jones ) [8, 9].

Несколько позже Тейлор ( Taylor ) разбил распределение направлений исхода спорадических метеоров несколько иначе [8, 9] — табл. 2.

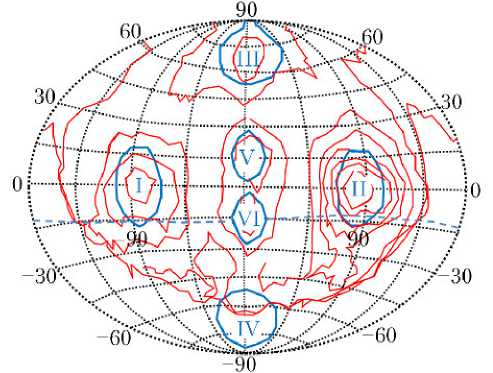
Рис. 2. Расположение основных радиантов спорадических потоков на небесной сфере: I — направление на Солнце; II — противосолнечное направление; III — северная тороидальная составляющая; IV — южная тороидальная составляющая; V — северная составляющая апекса орбитального движения Земли; VI — его южная составляющая

Таблица 2

вклад радиантов в поток спорадических метеороидов

Радиант (рис. 2)	Характеристика радианта (источника метеороидов)	Численность (по массе), %
		Браун, Джоунс	Тейлор
I	Солнечный ( hellion )	33	33
II	Антисолнечный ( anti-hellion )	33	36
III	Северный тороидальный ( North toroidal )	5	6
IV	Южный тороидальный ( South toroidal )	5	6
V	Северный апекс ( North Apex )	24	4
VI	Южный апекс ( South Apex )		4
—	Исходящие между основными радиантами	—	11

Способы и трудности измерения скорости метеороидов

В течение длительного времени для измерения скорости метеороидов использовались оптические (фотографические и телевизионные) и радиолокационные (РЛС) методы. Этими методами определяются начальные скорости метеоров (метеороидов, вошедших в верхние слои атмосферы).

Радиолокационные методы используются более широко. Так, например, в работе [9] анализируются данные, полученные при помощи РЛС HRMP ( Harvard Radio Meteor Project ) и ALTAIR ( the Advanced Research Project Agency Long Range Tracking and Instrumentation Radar ). Хотя обе РЛС используют существенно отличающиеся методы наблюдения ( HRMP — метеорного следа; ALTAIR — головного эха), получаемые оценки распределения скорости метеоров получаются близкими. Этот результат обусловлен физикой метеорной ионизации, которая определяется кинетической энергией метеороида, т. е. как его скоростью, так и массой. Основной трудностью определения скорости конкретного метеора, а, следовательно, и метеороида, является то, что неизвестна его масса. Кроме этого, при определении распределения скоростей метеороидов важную роль играет сама возможность их обнаружения при помощи радиолокатора [9], которая зависит от:

• •    плотности и пространственного распределения метеорной плазмы, определяющих процесс отражения радиосигнала;

• •    чувствительности самого радара;

• •    распределения радиантов спорадических метеоров.

Любой из радиолокаторов настраивается лишь на определённый диапазон масс метеороидов (минимальных масс для каждой скорости, при которых реализуема регистрация метеора) и определённый участок небесной сферы (радиантов метеороидов), которая, как известно, может содержать кроме спорадических метеороидов и частицы метеороидных потоков (см. табл. 1). Вклад метеорных ливней может заметно искажать как распределение массы спорадических метеороидов, так и распределение их скорости. В силу этого получаемые распределения скоростей, как правило, подвергаются необходимой коррекции. Кроме этого, при обработке данных, полученных с использованием радарных установок, необходимо учитывать рост скорости метеороидов из-за гравитации Земли (гравитационное фокусирование) и их замедление (торможение) в атмосфере Земли.

Трудности, возникающие при установлении скорости метеороида и связанные с неопределённостью его массы, проиллюстрируем данными, приведёнными в работе [10]. На рис. 3 приведены массы частиц и скорости соударений для всех воздействий, зарегистрированных датчиком (детектором) на межпланетном КА Ulysses с 2005 по 2007 гг.

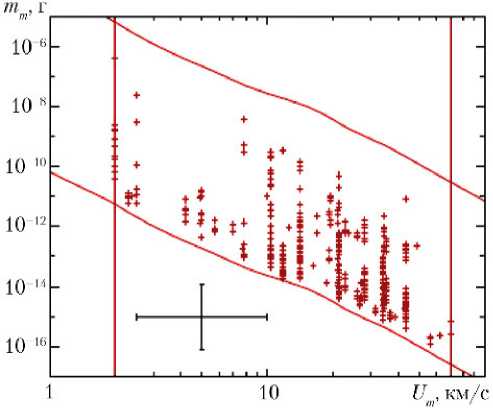
Рис. 3. Массы и скорости соударений для всех воздействий, зарегистрированных датчиком (сенсором) на

КА Ulysses с 2005 по 2007 гг. [10]

Примечание. Нижняя и верхняя сплошные линии определяют порог и предел чувствительности детектора, соответственно (в зависимости от массы и скорости метеороида). Вертикальные линии ограничивают диапазон скорости, на которую датчик был откалиброван (2…70 км/с). Согласно интервалам погрешности, приведённым на рисунке, коэффициент неопределённости для скорости Um равен 2, а для массы mm — 10.

Максимально фиксируемая масса 10–6 г, минимальная — 10–15 г. Соответствующие скорости — 2…70 км/с. Максимальное число частиц находится в диапазоне скоростей 10…17 км/с и 21…35 км/с.

Под действием силы притяжения Земли метеороид к моменту его входа в атмосферу Земли разгоняется до скорости [4, 11, 12]

v мa

2 GM v ² + ^З , ^м

R _З

где v _м , км/с — скорость метеороида на достаточно большом расстоянии от Земли, где силами притяжения Земли можно пренебречь; G = 6,637⋅10^–11 м³⋅кг^–1⋅с^–2 — гравитационная постоянная; M _З = 5,976⋅10²⁴ кг — масса Земли; R _З = 6,37⋅10⁶ м — средний радиус Земли.

Из соотношения (1) следует, что находящийся на достаточно большом расстоянии и неподвижный (т. е., v _м = 0) по отношению к Земле метеороид под действием сил притяжения Земли будет разгоняться и входить в атмосферу Земли со скоростью ~11,2 км/с, т. е. со второй космической скоростью. Таким образом, скорости метеороидов, влетающих в атмосферу Земли, лежат в пределах 11,2…72,0 км/с. Это справедливо для метеороидов, обращающихся вокруг Солнца (принадлежащих Солнечной системе). Следовательно, скорости встречи метеороидов с КА на низких орбитах вокруг Земли также лежат в диапазоне 11,2…72,0 км/с.

Высказываются гипотезы о возможном преобразовании эллиптических орбит метеороидов в гиперболические (из-за гравитационных воздействий) и о существовании частиц межзвёздного происхождения, т. е. частиц с непериодическим (гиперболическим) движением. Для таких частиц метеороидов скорости могут быть и больше 72 км/с. Некоторые исследователи, основываясь на фотографических, телевизионных и радиолокационных наблюдениях, полагали, что таких метеороидов 5–10%. Например, в работе [13] отмечено наличие особенности в области больших скоростей — ~1% метеоров имеют скорости больше 100 км/с. Но дискуссия [14] показала, что такие данные могут быть обусловлены низкой точностью измерений скорости метеоров из-за систематических и случайных погрешностей.

распределение скоростей метеороидов

Известно множество оценок как непосредственно скорости метеороидов (теоретических и экспериментальных), так и их распределений (зависимостей количество–скорость частиц). Результаты одной из первых оценок распределения метеоров (количества N ) по скорости U_m приведены в работе [15] и показаны на рис. 4.

По мере накопления данных измерений вид зависимости распределения метеороидов по скорости достаточно сильно изменился. Далее мы рассмотрим наиболее представительные, на наш взгляд, результаты таких оценок. Одно из наиболее цитируемых распределений, полученное по результатам фотографических наблюдений, приведено на рис. 5 [11].

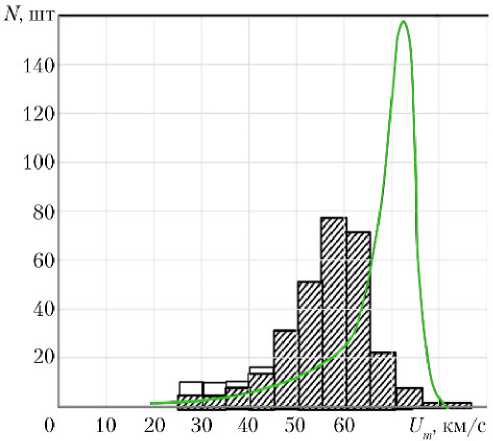
Рис. 4. Распределение метеоров по скорости из радиолокационных наблюдений [15]: гистограмма — величины скорости метеоров U_m, полученные при наблюдении; ^— — прогнозируемое распределение при параболической скорости метеороидов

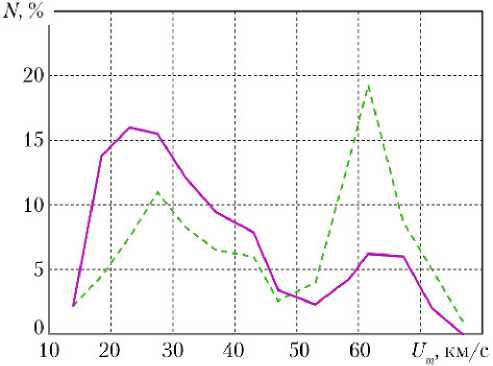
Рис. 5. Распределение скоростей метеороидов (внеатмосферных скоростей метеорных тел) по фотографическим наблюдениям [11]: ^— — яркие метеоры; ^^ ^^ — слабые метеоры

На рис. 5 представлены распределения скоростей метеороидов, вычисленные для двух типов метеоров: ярких и слабых. В отличие от данных на рис. 4, для этих распределений выделяются два максимума: первый — около 20–30 км/c; второй — в области 60–70 км/с. Первый максимум соответствует догоняющим Землю метеороидам, а второй — встречным. Между этими максимумами при скорости ~50 км/c имеется чётко выраженный минимум. В данном случае (рис. 5) на положении второго максимума сильно сказалось влияние метеороидного потока Персеид [11] (см. табл. 1), во время прохода через который проводились наблюдения (измерения). Наличие второго пика в интервале скоростей 60–80 км/с иногда также связывают с частицами, захваченными Солнцем и двигающимися по гиперболическим орбитам [13].

Радиолокатор позволяет обнаружить метеоры более слабые, чем это может сделать невооруженный глаз и тем более — фотографическая камера. В силу этого, определение скоростей и распределения скоростей метеороидов согласно данным радиолокационных наблюдений метеоров вызывает больше доверия у исследователей. На рис. 6 приведены результаты регистрации метеоров на РЛС HRMP (~14 000 наблюдений) из всех указанных выше (согласно Тейлору) источников (см. рис. 2), полученные в течение 1968–1969 синодического года [9].

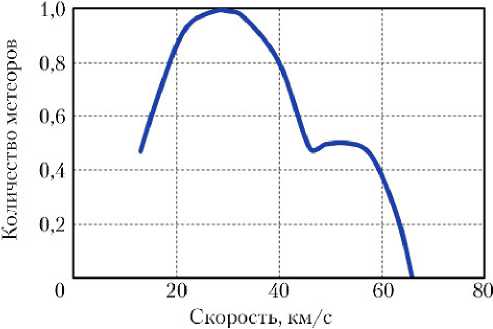
Рис. 6. Зависимость количества метеоров от их скорости по результатам измерений следа метеоров на РЛС HRMP в течение 1968–1969 синодического года [9]

Доминирующее влияние на пик в распределении скорости вблизи 32 км/с оказали медленно движущиеся метеороиды со стороны солнечного и анти-солнечного направлений (см. рис. 2).

Данные измерений с максимумом при более низких скоростях метеороидов были приведены в докладе на международной конференции [16]. Как были получены данные (фотографические, РЛС и др.), в докладе не указано. На гистограмме рис. 7 приведено распределение скоростей входа в атмосферу для 30 межпланетных пылевых частиц. Авторы [16] считают, что четыре частицы с низкой скоростью ( U_m ≤ 14 км/с) имеют астероидное происхождение, а 12 частиц с высокой скоростью ( U_m ≥ 18 км/с), вероятно, произошли от комет. Две частицы с U_m > 26 км/с на гистограмме не отображены.

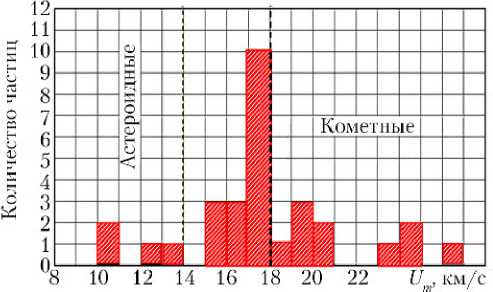
Рис. 7. Скорости входа в атмосферу межпланетных пылевых частиц [16]

Смещение максимума в сторону более низких скоростей (ср. с данными на рисунках выше) может быть связано с малым количеством измерений.

В Европейском космическом агентстве (ЕКА — ESA) используется распределение скорости метеороидов, основанное на данных, полученных на РЛС HRMP [17]. Набор исходных данных аналогичен использованному при построении зависимости на рис. 6 (14 000 наблюдений), только количество обработанных наблюдений метеоров увеличено до ~20 000. В результате значительного количества корректировок, которые выполнил Тейлор [18], были получены распределения скорости метеороидов, приведённые на рис. 8.

На рис. 8 зависимости для раз- личных высот приведены с учётом корректировки основного распределения на влияние гравитационного притяжения Земли. Как видим, положе- ние максимума в распределении L2

(при 1 а. е. без влияния притяжения Земли) пре-

18,8 км/с на 36 000 км и 17,2 км/с — без влияния притяжения Земли. В работе [18] рекомендовано при оценке опасности столкновения КА с метеороидом использовать среднее значение относительной скорости, равное 20 км·с–1.

При построении метеороидных моделей используются соответствующие распределения скоростей метеороидов — как усреднённое для спорадического фона, так и отдельные распределения для потоков.

Большинство используемых NASA метеороидных моделей — NASA Technical Memorandum 4527 [19] и NASA Space Station Program SSP 30425 — для прогнозирования потока метеороидов вблизи Земли основаны на модели Грюна (Grün) [5]. Модель Грюна не содержит направленности, т. е. среда в части метеороидов рассматривается изотропной. Распределение скоростей не используется, а модель построена в предположении, что средняя скорость метеороидов равна 20 км/с. NASA для КА на орбите Земли совместно с моделью Грюна использовало распределения скоростей со средними значениями 17 и 19 км/с. Как отмечено в работе [8], оказалось, что эти распределения скоростей плохо работают с потоками, определён- ными согласно зависимости Грюна. Причина виделась в том, что кратеро-образование (т. е. разрушающее воздействие) зависит от квадрата скорости метеороидов.

терпело область

смещение в более низких

скоростей (ср. с зависимостью на рис. 6, где максимум наблюдается около 30 км/с). При этом из анализа следует, что учёт гравитационного притяжения (в данном случае, Земли) смещает распределения в область более высоких скоростей.

0.05

о х х

я

в

0,04

0,03

0,02

0,01

Были получены ющие средние

следу (средне

-

-

интегральные) на различных 22,7 км/с на 21,7 км/с на

скорости высотах: 400 км;

1 500 км;

Рис.

Орбита

—£2 (1 а. с.)

—Геостационарная

........Солнечно-синхронная

_...мкс

8. Нормализованное распределение скорости

50 Um, км/с метеороидов согласно

HRMP-измерениям для различных расстояний от поверхности Земли [17]: МКС — 400 км; солнечно-синхронная орбита — 1 500 км; геостационарная орбита — 36 000 км; L2 соответствует распределению при 1 а. е. без влияния притяжения Земли

В статье [8] рассматриваются некоторые аспекты известной метеороидной инженерной модели MEM [5] для межпланетных КА на расстояниях 0,2…2,0 а. е., а также приведено распределение для скорости метеороидов (рис. 9), полученное из теории и проверяемое наблюдениями. На рисунке представлено интегральное распределение, а в табл. 3 приведены средние значения скорости на каждую из ориентированных поверхностей (плоскостей) КА (согласно MEM версии 1.0.).

Моделировались потоки на КА кубической формы, находящемся на почти круговой гелиоцентрической орбите и на расстоянии 1 а. е. Рассматривался интегральный поток для частиц с массой m ≥ 10^–6 г (массового порога не менее 10^–6 г). Поскольку при нулевом эксцентриситете вектор положения и вектор скорости перпендикулярны, то поверхности правого и левого бортов будут, соответственно, эквивалентны солнечной и антисолнечной поверхностям (табл. 4). Если будет выбрана эллиптическая гелиоцентрическая орбита, то на эти поверхности будут поступать потоки с отличающимися значениями скорости.

Отметим, что для усреднённого потока модель MEM предсказывает средневзвешенную скорость метеороидов 23,9 км/с для Земли (ср. с величиной из модели Грюна — 20 км/с). В работе отмечается, что это новое значение согласуется с данными, полученными при наблюдениях с использованием Канадского Орбитального Метеорного Радара (Canadian Meteor Orbit Radar — CMOR) [8].

В работах [5, 20]

проведено

сопоставление

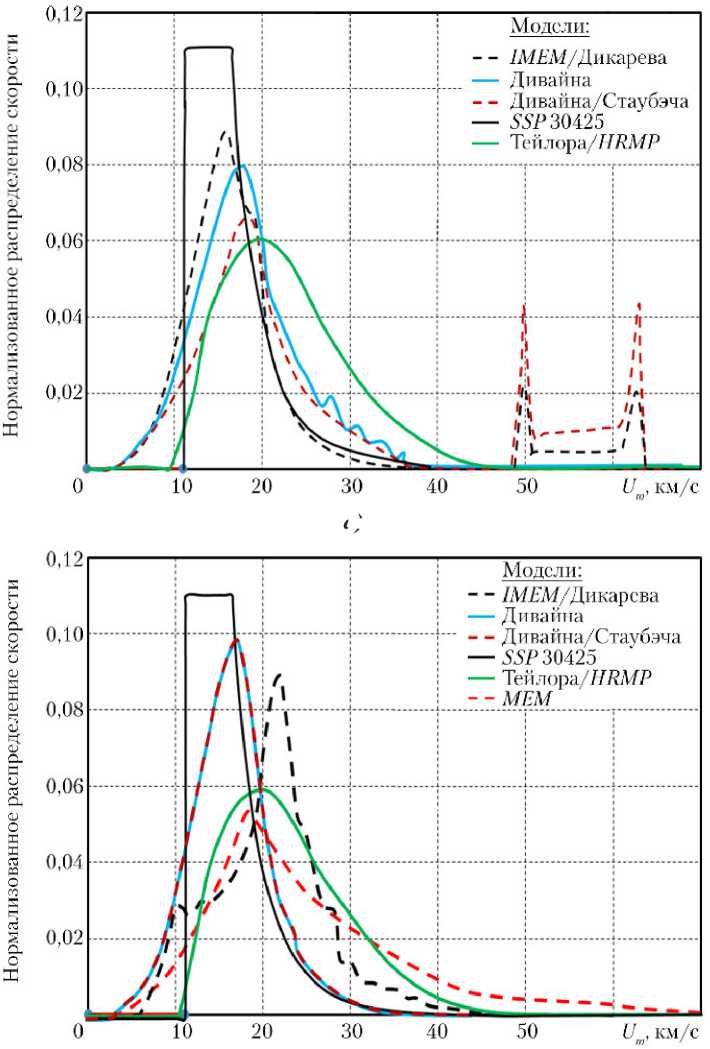
различных метеороидных моделей, используемых ESA , в т. ч. рассмотрены и используемые распределения для скорости. На рис. 10 представлены нормализованные распределения скорости метеороидов для низких орбит ( LEO — Low Earth Orbits ) (орбита МКС) при массовых порогах m ≥ 10^–12 г и m ≥ 10^–3 г.

Как указано в работе [5], распределения скорости в моделях ИМЭМ/Ди-карева ( IMEM/Dikarev ), Дивайна ( Divine ) и Дивайна/Стаубэча ( Divine/Staubach ) построены согласно принятым в них популяциям (классам) метеороидов, имеющим свои индивидуальные характеристики. Каждая популяция имеет собственную направленность и распределение скорости. Результирующее распределение не является изотропным.

Распределения скорости, устанавливаемые SSP 30425 [21] и Тейлор/ HRMP [18], как отмечено в работе [5], могут использоваться совместно с изотропным распределением плотности потока частиц Грюна [22]. Достаточно искусственное распределение для скорости SSP 30425 , созданное для инженерных целей программы МКС, было одним из первых предложений для распределения скорости.

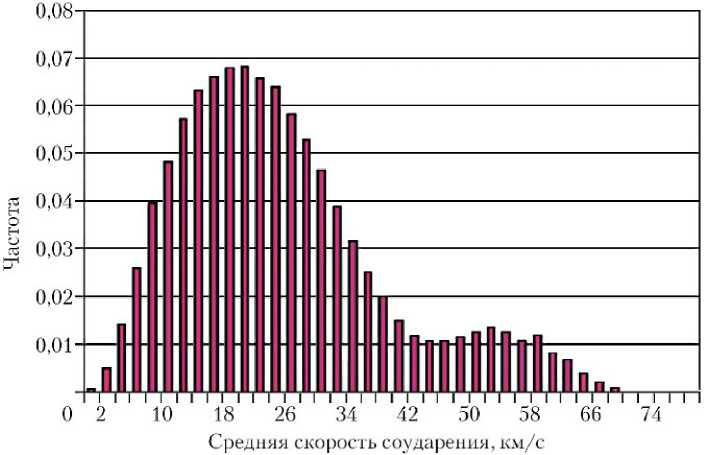
Рис. 9. Суммарное распределение скорости метеороидов согласно MEM [8]

Таблица 3

Средняя скорость соударения (км/с) с ориентированной поверхностью

Лобовая ( Ram )	Тыльная ( Wake )	Северная (верх) ( North )	Южная (низ) ( South )	Правый борт ( Starboard )	Левый борт ( Port )	Солнечная ( Sun )	Антисолнечная ( Anti-Sun )	Земля ( Earth )
26,0	21,6	24,0	24,1	24,2	24,0	24,0	24,2	21,4

Для описания

этого распределения

SSP 30425 в метеороидной модели

NASA [12,   23,   19] использовалось следующее соотношение:

0,112

n ( V ) =   3,328⋅10⁵⋅ V ^-5,34

1,695⋅104

если 11,1 ≤ U_m < 16,3км/с если 16,3 ≤ U_m < 55,0км/с .

если 55,0 ≤ U_m < 72,2 км/с

Согласно соотношению (2), средняя скорость метеороида 16,85 км/с; по отношению к орбитальному аппарату средняя скорость составляет ~19 км/с.

а)

б)

Рис. 10. Нормализованное распределение скорости метеороидов для орбит типа МКС (ISS): а — m ≥ 10^–12 г; б — m ≥ 10^–3 г; m — масса метеороидов

Распределение с нижним порогом m ≥ 10^–12 г было выбрано, чтобы показать вклад высокой скорости межзвёздного источника в моделях Дивайна/Стоубэ-ча и ИМЭМ/Дикарева. Согласно этим моделям, межзвёздные частицы вносят вклад только для масс метеороидов меньше 10^–9 г. Модель MEM используется только для масс больше 10^–6 г, и поэтому на рис. 10, а соответствующая зависимость отсутствует.

Как видим, распределения скоростей из различных моделей заметно различаются. Для области высоких масс метеороидов (> 10–3 г) график нормализованного распределения скорости для модели ИМЭМ/Дикарев имеет максимум при более высоких скоростях в сравнении с другими моделями.

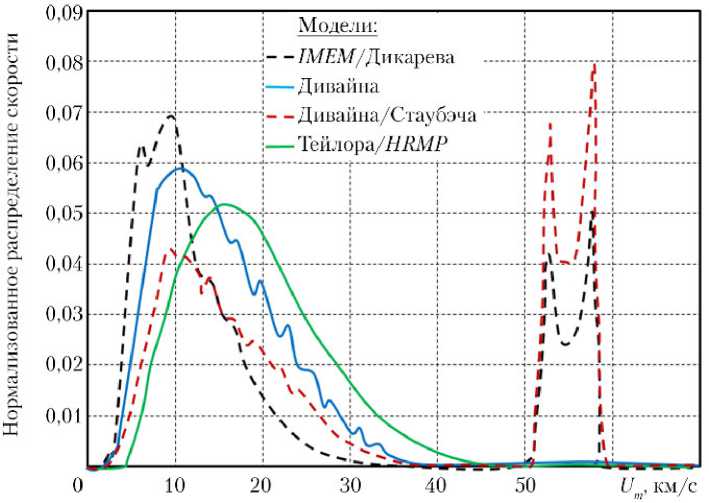
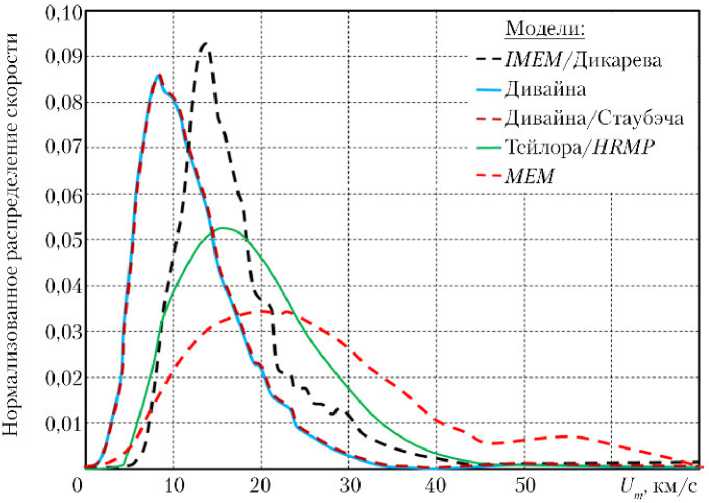
Нормализованные распределения скорости для высоких орбит ( GEO — Geostationary Earth orbits ) приведены на рис. 11.

Как видим, по сравнению с низкими орбитами ( LEO ), распределения для высоких орбит ( GEO ) заметным образом смещаются в сторону более низких скоростей. Это является результатом уменьшения гравитационного воздействия Земли и более низкой скорости КА на высоких орбитах. Распределение скоростей для разных массовых порогов указывает на аналогичное поведение на LEO и GEO .

а)

б)

Рис.

11. Нормализованное распределение скорости для высоких орбит (GEO):

а — m ≥ 10–12 г; б — m ≥ 10–3 г

предполагалась фиксированной по отношению к Солнцу и равной 26 км/с. Задано и фиксированное направление поступления этой составляющей в эклиптической системе координат с центром на Солнце: 77 ° долготы и -3 ° широты для модели ИМЭМ/Дикарев.

Скорости частиц (как и потоки) межзвёздной пыли относительно Земли определяются сложением движения частиц межзвёздной пыли и Земли относительно Солнца. Дополнительное движение КА добавляет вторые пики между 48 и 65 км/с (см. рис. 10, а и 11, а . Результаты на этих рисунках приведены по состоянию на 21 марта, когда вклад межзвёздной пыли и относительные скорости находятся около максимума. Модели также предсказывают исчезновение потоков межзвёздной пыли для больших масс. Из-за отсутствия этой популяции метеороидов максимумы при высоких скоростях для m > 10^–3 г не проявляются (рис. 10, б и 11, б ).

В табл. 4 и 5 приведены средние скорости соударений на ориентированные поверхности

Для нижнего порога массы (m ≥ 10–12 г) распределения скорости для моделей Дивайна/Стаубэча и ИМЭМ/Дикарева имеют локальные максимумы между 50 и 65 км/с. Этот результат для указанных моделей обусловлен учётом в них популяции межзвёздной пыли, которая даёт заметный вклад от метеороидов небольших масс. Масштабы вклада межзвёздной пыли и скорость удара зависят от времени года. В модели непосредственно для популяции межзвёздной пыли скорость для потоков метеороидов с массовыми порогами m > 10–6 г (табл. 4) и m > 10–3 г (табл. 5).

Скорости соударений, предсказанные моделями Грюн/HRMP и MEM, не зависят от массы частиц для всего диапазона их применимости. Это объясняет одинаковые значения согласно этим моделям в табл. 4 и 5. Предсказанные скорости, согласно моделям Дивайна (Divine) и Дивайна/Стаубэча (Divine/Staubach), отличаются друг от друга. Эти модели должны, главным образом, отличаться для масс меньших, чем пороговое значение 10–6 г в табл. 4. Поскольку прогноз соответствующих потоков на ориентированные поверхности, по существу, идентичен, различия в табл. 4 и 5 могут быть следствием, вытекающим из различных численных реализаций этих моделей.

Большинство моделей прогнозируют более высокую среднюю скорость соударений для передней поверхности и более низкую скорость — для задней. Модель MEM , в сравнении с другими моделями, обычно предсказывает более высокие скорости соударения. Средние скорости соударений, согласно этой модели, изменяются лишь незначительно для различных ориентаций поверхности. Необычным является то, что предсказываемые скорости соударения для задних (тыльных) поверхностей могут быть больше, чем для передних (табл. 4 и 5).

Для m > 10^–3 г модель ИМЭМ/Дика-рев ( IMEM/Dikarev ) прогнозирует наиболее высокие абсолютные значения скорости среди всех моделей для переднего и правого бокового направлений. Это известная (характерная) особенность этой модели, обусловленная взаимосвязью характерной скорости и интегрального потока при этих массах частиц — более высокие скорости, но более низкие потоки [5].

В ГОСТ [24] при фиксированном угле е между вектором скорости спорадического метеорного тела U_m и вектором, противоположным вектору орбитальной скорости Земли V _З (в градусах), используется условное распределение скоростей спорадических метеорных тел P _е ( U m ) ). Распределение скоростей спорадических метеорных тел массой m > 10^–6 г приведены в стандарте [24], согласно которому при малых е (Земля встречает метеороид — рис. 12) максимум в распределении числа частиц приходится на скорости метеороидов 64–66 км/с (~15%).

Таблица 4

Скорость соударения для ориентированных поверхностей (км/с), орбита мкС, m > 10^–6г [5]

Модель	Передняя поверхность Ram	Правая (боковая) Starboard	Верхняя (Зенит) Zenith	Тыльная кильватерная Wake
Грюн/ HRMP	21,1	18,9	18,8	15,3
Дивайн	20,1	17,5	17,3	13,2
Дивайн/Стаубэч	20,3	17,8	17,6	13,2
ИМЭМ/Дикарев	18,3	16,0	15,8	12,0
MEM	23,1	23,2	23,1	23,6

Таблица 5

Скорость соударения для ориентированных поверхностей (км/с), орбита мкС, m > 10^–3 г. [5]

Модель	Передняя поверхность Ram	Правая (боковая) Starboard	Верхняя (Зенит) Zenith	Тыльная кильватерная Wake
Грюн/ HRMP	21,1	18,9	18,8	15,3
Дивайн	18,5	16,7	15,9	11,3
Дивайн/Стаубэч	18,1	16,4	15,6	11,2
ИМЭМ/Дикарев	24,6	26,7	20,6	14,9
MEM	23,1	23,2	23,1	23,6

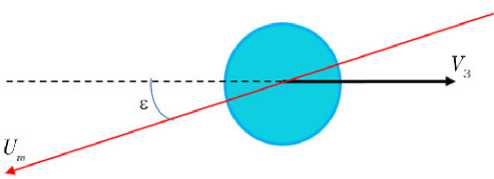
Рис. 12. Схема встречи метеороида с Землей

Второй максимум на скорости 10–12 км/с — 8,21%. При больших значениях е — 170-180 ° (метеороид догоняет Землю) максимум в распределении наблюдается для скоростей 14–16 км/с — 48,9%. Второй максимум в этом случае отсутствует. Для «боковых» метеороидов максимум в распределении принадлежит скоростям 26–28 км/с.

Скорости относительно Земли метеорных тел массой m ≤ 10^–6 в ГОСТ [24] приняты равными 20 км/с.

Как видим, данные по скоростям метеороидов в околоземном космическом пространстве постоянно уточняются.

Ввиду этого при определении вероятности неповреждения (ВНП) КА при небольшом времени эксплуатации (полёта) с целью минимизации массы противометеороидной защиты выбор интегрального потока [2] и задание скорости для БП требуют проведения достаточно тщательного анализа условий нахождения КА на орбите.

распределение скоростей частиц космического мусора

При анализе техногенного загрязнения околоземного космического пространства (ОКП) одним из важных вопросов, как и в случае метеороидов, является оценка вероятности столкновения КА с КМ с оценкой возможных последствий. Особенно остро этот вопрос стоит в области низких орбит с высотами до 2 000 км, а также в области геостационарных орбит, где техногенное загрязнение является максимальным. Последствия столкновений КА c КМ существенным образом зависят от их скорости [1]. Основная трудность в определении скорости столкновений с частицами КМ обусловлена недостатком экспериментальных данных. Имеющаяся информация от измерений получена в относительно небольших районах многомерной области ОКП «высота точки – широта точки – размеры КМ – время» [12]. Поэтому для определения характеристик техногенного загрязнения в различных точках ОКП привлекается дополнительная (априорная) информация. Эффективное использование экспериментальных данных и априорной информации — основная проблема, которая решается при построении моделей КМ.

Наиболее известными моделями, используемыми для определения плотности потока и скорости техногенных частиц КМ, являются российская модель SDPA (Space Debris Prediction and Analysis) (Назаренко, Мечников, Юрасов) [12, 25] и американская модель NASA-90 (Kessler, Reynolds, Anz-Meador) [19, 23]. Согласно этим моделям разработано специальное программное обеспечение, использующее постоянно обновляемые базы данных. Новая информация для баз данных поступает от соответствующих орбитальных аппаратов. Учитываются параметры орбиты, ориентация поверхности, плотность потока, направление и величина скорости частиц КМ.

SDPA — полуаналитическая стохастическая модель для среднесрочного и долгосрочного прогнозирования наиболее опасного техногенного КМ размером более 1 мм, применяемая для построения пространственных распределений концентрации и характеристик скорости, а также для оценки риска столкновений. Используются компьютерные программы SDPA-E и SDPA-F [25]. Программа SDPA-E позволяет вычислить зависимость скорости столкновений от её направления относительно КА, а также среднюю скорость столкновений КА с КМ.

В процессе исследований с использованием SDPA установлено, что радиальная составляющая скорости КМ на один-два порядка меньше тангенциальной. Этот факт позволяет существенно упростить статистические исследования возможных столкновений на основе допущения, что поток КМ является плоским. Другая особенность рассматриваемого распределения — его зависимость от высоты. На малых высотах радиальная составляющая находится в интервале ±0,2 км/с. С увеличением высоты интервал возможных значений увеличивается, достигая 1 км/с. Такой характер высотной зависимости объясняется влиянием орбит с большими эксцентриситетами.

Для примера на рис. 13 представлены нормированные статистические угловые распределения плотности потока (кривая 1 ) и зависимость относительной скорости КМ от её направления (угла а ) (кривая 2 ) для КА с элементами круговой орбиты — высота 400 км, наклонение 51,6 ° . Угол а отсчитывается в горизонтальной плоскости от вектора скорости КА.

В модели NASA-90 ненормализованное распределение скорости столкновения КМ с КА выражено функцией Кесслера f ( v ) [19, 23]:

f ( v ) = (2 vv ₀ - v ²){ G exp(-(( v - Av ₀ )/( Bv ₀ ))²) +

+ F exp{-(( v - Dv ₀ )/ Ev ₀ ))²} + HC (4 vv ₀ - v ²).

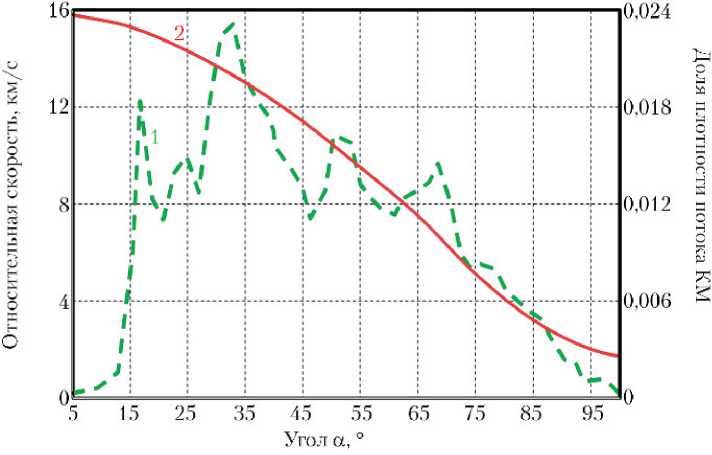
Рис. 13. Нормированные статистические угловые распределения [12, 26]:

1 — нормированная плотность потока космического мусора (КМ) — правая шкала;

2 — зависимость относительной скорости от её направления — левая шкала

Коэффициенты A , B , C , D , E , F , G , H и v ₀ в функции (3) зависят от наклона и высоты орбиты. Выражения для коэффициентов можно найти в работах [19, 23]. Если f ( v ) < 0, то f ( v ) = 0.

Функция Кесслера f ( v ) численно нормализуется с использованием соотношения:

f ‘ ( v ) =

f ⁽ v )

∞

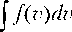
Нормализованная функция f '( v ) определяет долю КМ над любым интервалом скорости шириной в 1 км/с. В качестве примера на рис. 14 приведены распределения f ' ( v ) для КА с отличающимся наклонением орбиты. Как видим, с увеличением наклонения орбиты максимум распределения (доля частиц КМ) смещается в область более высоких скоростей. При определении ВНП КА эти данные указывают на необходимость учёта параметров орбиты аппарата.

Известны и используются относительно простые методики для оценки скорости фрагментов КМ. Описание одного из этих методов представлено в работе [29]. В предлагаемой методике частица КМ и КА рассматриваются в виде материальных точек. Общая схема взаимодействия частицы КМ и КА при их движении по орбитам приведена на рис. 15.

Для нахождения относительной скорости в точке встречи частицы КМ и КА задаются следующие параметры орбит, по которым двигаются КА и частица КМ:

• •    наклонение;

• •    высота перигея;

• •    высота апогея.

Принимается допущение о равномерном распределении космического мусора по орбитам и равновероятной встрече в каждой точке орбиты с КА. Как и в случае SDPA, радиальная составляющая вектора скорости исключена из рассмотре- ния: поток КМ считается плоским.

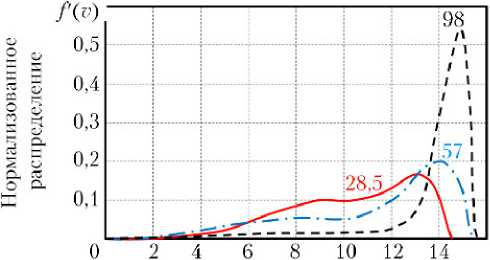
Скорость KM относительно KA (км/с)

Рис. 14. Нормализованное распределение скорости столкновения как функция скорости КМ для КА с наклонением орбиты 28,5; 57 и 98° [19,27,28]

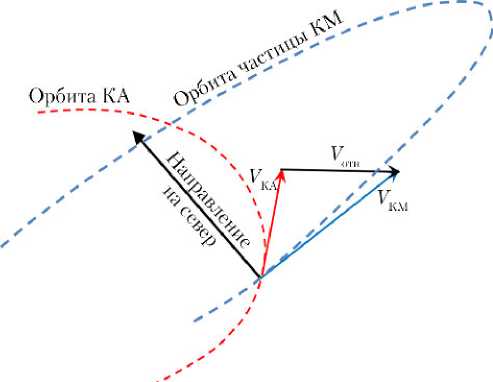
Рис. 15. Схема взаимодействия частиц КМ c КА

В результате численных исследований авторами [29] получены гистограммы относительной частоты распределения скоростей КМ. Максимумы в распределении приходятся на скорости:

• •    2 км/с (~25%) и 7 км/с (~24%) — для случая низких круговых орбит КА ( h = 400 км);

• •    2,5 км/с (~17,5%) и 13,5 км/с (~19%) — для практически круговых орбит КА ГЛОНАСС ( h = 19 180 км).

Как видим, скорость встречи КА с КМ существенным образом зависит от высоты орбиты.

В работе [23] приведено сопоставление плотности потока метеороидов и частиц КМ в зависимости от их скорости для одной из орбит КА — рис. 16 (к сожалению, параметры орбиты и КА в работе не указаны). Не упоминается также минимальная масса (размеры) частиц метеороидов и КМ.

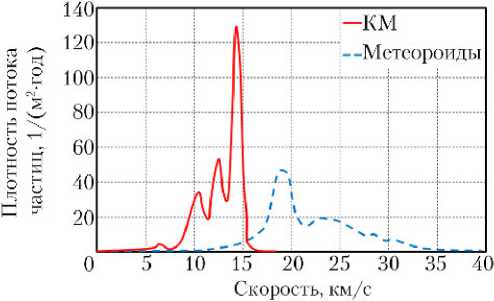
Рис. 16. Диаграмма зависимости потока частиц метеороидов и космического мусора от скорости

Согласно дифференциальной диаграмме на рис. 16, интеграл, т. е. суммарная плотность потока частиц для всех скоростей, составляет:

• •    для частиц метеороидов ~300 1/(м²·год);

• •    для частиц КМ ~200 1/(м²·год).

При этом, согласно оценкам автора [23], вероятность повреждения КА со сроком эксплуатации семь лет составляет: метеороидами — 0,1%; частицами КМ — 3,43%.

Приведённый пример указывает на важность учёта потока частиц КМ при определении вероятности повреждения (неповреждения) КА.

Какие скорости метеороидов и КМ использовались и используются при определении ВНП? Поскольку, как правило, при вычислении ВНП вид БПУ не указывается, в литературе отсутствуют и данные об используемых для определения критических размеров частиц скоростях как метеороидов, так и частиц КМ.

Кроме этого, часто критические размеры частиц при определённой их скорости для фиксированной защиты от высокоскоростного удара указываются при условии, что защита «способна защитить конструкцию герметичного корпуса от столкновения». Естественно, понятие ВНП в этом случае не используется. Непонятным в этом случае является и термин «от столкновения». Так, например, в работе [30] для пакета защиты на станциях «Салют» указывается критический размер для алюминиевых частиц (сферических) «при соударении со скоростью 8 км/с по нормали к поверхности» . Почему используется эта скорость, в статье [30] не объясняется. Возможно, и наиболее вероятно, что защита строилась в предположении определяющего воздействия частиц КМ. Тогда скорость частиц, равную 8 км/с, можно считать достаточно корректной. В случае применения двухслойных углепластиковых сотовых панелей на модулях «Квант-2», «Кристалл», «Спектр» и «Природа» космического комплекса «Мир» критический диаметр высокоскоростной частицы, не пробивающей конструкцию защитных экранов и вафельную конструкцию герметичного корпуса, также определялся при нормальной скорости соударения 8 км/с [30, 31].

При оценках защиты для МКС (обеспечение условий безопасности экипажа) была задана ВНП для функциональногрузового блока станции, равная 0,979. Это значение ВНП соответствовало (из предварительных расчётов) критическому диаметру частиц 10 мм при угле соударения 45 ° и скорости частицы 7 км/с. Информация в работе [30], поясняющая выбор таких параметров, также отсутствует.

заключение

Из приведённых данных следует, что при определении вероятности не-повреждения КА метеороидами или частицами космического мусора значение скорости, используемой в предельных баллистических уравнениях для определения критического размера (массы) частиц, должно согласовываться с моделью плотности потока рассматриваемых высокоскоростных частиц (метеороидов и/или КМ).

При этом необходимо учитывать анизотропию в скорости метеороидов и частиц КМ по отношению к КА, возникающую в результате векторного суммирования их скоростей.

Скорости встречи метеороидов с КА на низких орбитах вокруг Земли лежат в диапазоне 11,2…72,0 км/с. Максимум в нормализованных распределениях скорости на высотах орбит до 36 000 км соответствует скорости в 18±2 км/с (наиболее вероятная скорость).

Скорости встречи частиц КМ с КА в ОКП существенным образом зависят от параметров орбиты КА и лежат в диапазоне 4,0..16,0 км/с. Для низких круговых орбит наиболее вероятная скорость удара частиц КМ составляет 8±2 км/с.