Скорость убывания массы решения задачи Коши дважды нелинейного параболического уравнения с абсорбцией
Автор: Бесаева Зарина Вячеславовна, Тедеев Анатолий Федорович
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 1 т.22, 2020 года.
Бесплатный доступ
В работе изучается задача Коши для широкого класса квазилнейных параболических уравнений второго порядка с неоднородной плотностью и абсорбцией. Хорошо известно, что для рассматриваемого класса задач без абсорбции и при условии, что плотность стремится к нулю не слишком быстро, имеет место закон сохранения тотальной массы. Однако этот факт не всегда имеет место при наличии абсорбции. В данной работе найдены точные условия на характер нелинейности и поведения неоднородной плотности на бесконечности, которые гарантируют стремление к нулю тотальной массы решения при неограниченном возрастании времени. Другими словами, найден критерий стабилизации к нулю тотальной массы решения в терминах критических показателей. С помощью полученных результатов и локальных оценок типа Нэша - Мозера выводятся точные оценки решения в равномерной метрике.
Задача коши, вырождающиеся параболические уравнения, неоднородная плотность, абсорбция, критические показатели
Короткий адрес: https://sciup.org/143170625
IDR: 143170625 | УДК: 517.944 | DOI: 10.23671/VNC.2020.1.57535
Текст научной статьи Скорость убывания массы решения задачи Коши дважды нелинейного параболического уравнения с абсорбцией
В данной работе рассматривается задачи Коши для решения квазилинейных вырождающихся параболических уравнений вида
p( | x | )u t — div A(x, t, u, V u) + g(x, t, u) = 0, (1-1)
(x, t) E s : R N x (0, то ), удовлетворяющих начальному условию
u(x, 0) = u o (x), x E R N , p(s) > 0, 0 < s < то , u o (x) > 0, pu o (x) E L 1 ( R N ) - (1-2)
На протяжении всей работы предполагается выполнение следующих условий. Вектор-функция A (x, t, u, £) = (A i (x, t, u, ^), - - -, An (x, t, u, ^)): R N x R + x R x R N ^ R N и g(x, t, u):
(c) 2020 Бесаева З. В., Тедеев А. Ф.
RN x R+ x R ^ R удовлетворяют условию Каратеодори, т. е. измеримы по переменным (x, t) Е RN +1 и непрерывны соответственно по переменным u Е R, £ G RN. Функция p(s): R+ ^ R+ непрерывна монотонно убывающая функция по s Е [0, то]. Кроме того, предполагается выполнение следующих структурных условий: существуют положительные постоянные ^i и р2 такие, что
A(x,t,u,O^ > N£\p |u|m-1,
IA (x,t,u,O\^ №\£\p-i |u|m-1,
^2\u\4 ^ signu, g(x,t,U ^ №\u\q.
Кроме того, выполнено условия монотонности: для любых двух векторов £ = (^ 1 ,... ,^n ) и П = (n i ,..., n N ), для любого и Е R , т. е. для (x, t) Е R N x R + выполнены неравенства
(A(x, t, u, £) - A(x, t, u, n)) (£ — n) > 0,
[g(x, t, ui) - g(x, t, U2)] [ui - U2] > 0(1
для всех £ i и П 2 из R N . Постоянные p, m, q удовлетворяют следующим условиям:
1
1, p > 1.
Предположим также, что функция p(s) для всех s > 0 удовлетворяет условию H : Существуют такие положительные постоянные l i и l ^ , причем l i < p, что функция p(s)s l 1 монотонно убывает, а функция p^s1- 2 монотонно растет.
Примером уравнения (1.1) является
p( \ x \ )u t = A m,p u — \ u \ q - i u, (1.9)
где
A m,p u := div ( \ u \ m - i \V u \ p - 2 V u )
и p(s) ~ s—l, s ^ 1, 0 < l < p. Здесь символ ~ — наличие двусторонней оценки cis-l < p(s) < c2s-l (Vs ^ 1, ci,c2 > 0). (1.10)
Для уравнения
p( \ x \ )u t = A m,p u (1.11)
с конечным интегралом H pu g ^ i : = JrN pu g dx, который принято называть тотальной массой или просто массой начальной функции , при выполнении, например, условия (1.10), справедлив закон сохранения «массы» (см. [1]):
llpuo h i = ||pu(t) h i (Vt>0).
В работе [1] для задачи (1.1), (1.2) с p(x) = (1 + \x\)-l, l < p, g(x,t, u) = 0 установлена равномерная оценка решения p-l - N-l
|u(t)| ^ := |u(x,t)| L ^ ( R N ) < C || Pu o H i l t hl (1.12)
для любых t > 0. Кроме того, из [1] следует, что если suppu0(x) C Br0(0) := {x Е RN/\x\ < R0}, R0 < то, то supp u(x,t) принадлежит шару BR(t) (0), где p+m-3 1
R(t)=4R + Y ^ u o P ^ i hl t . (1.13)
Однако наличие абсорбирующего слагаемого в уравнении (1.1) может существенно изменить качественные свойства решений. В частности, тотальная масса ||up | i решения может стремиться к нулю при t ^ то . Указанный феномен имеет место при p(s) = 1. В этом случае (1.9) допускает «плоское» решение вида
U (t) = C (p)(t + T ) - q - 1 .
Кроме того, для (1.9) справедлива также оценка (1.12) с l = 0. Таким образом, по теореме сравнения для решения задачи Коши (1.9), (1.2) имеет место оценка p -N - 1
| u(t) | ^ < C min ||u o | e t в , t q - 1| (1.14)
при t > 1. Здесь в = N (p + m — 3) + p.
Очевидно, что в (1.14) при достаточно больших t
||u(t )|k < Ct — q - 1 (1.15)
и условии, что NN < q-— i , т. е.
p q < q = p + m — 2 + N.
Оказывается, что в этом случае | u(t) | i ^ 0 при t ^ то и можно указать точную оценку массы решения. Подойдем теперь к этой же проблеме шире. Из оценки L i — L ^ типа Нэша — Мозера (см., например, [2]), имеем
p
| u(t) l - < C | | u(^ t - в . (1.16)
Теперь, если иметь точную по порядку оценку массы при достаточно больших t , то можно снова прийти к тому же результату (1.14). Однако такой подход может быть применен к более широкому классу уравнений, а оценка массы решения, как это будет видно ниже, сводится к локальным энергетическим оценкам, имеющим в определенном смысле универсальный характер. В данной работе используются подходы работ [2–5] при изучении точного поведения тотальной массы решения задачи (1.1), (1.2) при t ^ то .
Отметим, что исследование уравнения (1.11), представляет независимый интерес. Известно, что [6-8] в зависимости от скорости стремления к нулю на бесконечности р(х) решение задачи (1.1), (1.2) обладает рядом нестандартных свойств. Укажем здесь на работы [9–17]. Оценкам массы решения для различных классов вырождающихся параболических уравнений были посвящены также работы [9, 10] (см. также имеющуюся там литературу). Прежде чем перейти к формулировкам основных результатов работы введем понятие решения (обобщенного) задачи (1.1), (1.2).
Решением задачи (1.1), (1.2) в S = R N х (0, то ) будем называть функцию u(x,t), которая для любых t > 0, T > t, о = p + pm— 2 удовлетворяет условиям и " (x, t), принадлежит классу
L p (t,T) х W p 1 ( R N ) П C ( [t,T ] : L i+ CT,p(N ) ( R N )) П L q + " ( (t,T),L q + " )
и удовлетворяет интегральному тождеству
TN
/ / (( - u(x,T)п т (x, т)p( | x | ) ) + ^ A i (x,t,u, V u)n x i + g(x, t, u)n(x, т)} dxdT (1.17)
t R N i =1
1 1
для любой п(х,т ) = 0 при т = t и т = T , п ст (x,t),n T € L 1+ a (p( | x | )(t,T) : L 1+ 1 ,p( | x | )),
σ
П ^ (x,t) € L p ((t,T) x W p 1 ( R N )) П L q + 1 ((t,T),L q + 1 ).
σσ
Кроме того, u(x, t) удовлетворяет начальному условию
R N
R N
Существование решения (1.1), (1.2) доказывается точно также, как в работе [1]. Единственность энергетического решения в случае p(s) = const и начально-краевой задачи Коши — Дирихле хорошо известно. Таким образом, если supp u g С B r 0 , т. е. для начальной функции с компактным носителем единственность решения (1.1), (1,2) гарантирована.
Основные результаты работы содержаться в теоремах 1.1–1.5.
Обозначим Ф(R) := R N- q - ( p + m - 2) p(R).
Теорема 1.1. Пусть u(x,t ) — решение задачи (1.1) , (1.2) в R N x (0, то ) и выполнены условия (1.3) - (1.7) и условие H . Предположим, что Ф(R) для всех R > 0 строго монотонно убывает и
Ф(R) ^ 0, R ^то .
(1.18)
Тогда
E(t) := /
R N
p( | x | )u(x, t) dx ^ y
/
p( | x | )u o (x) dx + YФ(R(t)),
(1.19)
R N W,R(t)
___ p(q-i)
где R(t) — функция, определяемая из соотношения p(R)R q - ( p +m - 2) для любого t > 0 .
Теорема 1.2. Пусть u(x,t ) — решение задачи (1.1), (1.2) в R N x (0, то ) и выполнены условия (1.3) - (1.7) и условие H . Предположим, что существуют положительные постоянные C, C 2 такие, что для всех R > 0
C i ^ Ф(R) ^ C 2 .
(1.20)
Тогда при достаточно больших значениях t выполняется оценка
1_
E(t) < Y[ln t] q - 1 .
(1.21)
Теорема 1.3. Пусть u(x,t) —решение задачи (1.1) , (1.2) в R N x (0, то ) и выполнены условия (1.3) - (1.8), q > q ^ , suppu g С B r 0 , p( | x | ) = const(1 + | x | ) — l , 0 < l < p. Тогда для достаточно больших значениий времени t существует Y = y (||uop||i, №, №) такое, что
E(t) > yE(0).
(1.22)
Теорема 1.4. Пусть u(x, t) —решение задачи (1.1), (1.2) в RN х (0, то), suppug С Br0 и выполнены условия (1.3)-(1.7), условие H, q = p + m — 2. Тогда для достаточно больших t имеет место оценка p+m-2 - 1
E(t) C Y[p(ln t)] p+m-3 (ln t) N t- p+m-3 (1.23)
Теорема 1.5. Пусть u(x, t) — решение задачи (1.1), (1.2) в R N х (0, то ) , suppu g С Br0 , ||u g p | i+ 9 < то для некоторого 6 > 0 , 1 < q < p + m — 2 . Пусть еще выполнены условия (1.3) - (1.7) и условие H . Тогда существует постоянная C , не зависящая от t, такая, что
E(t) C Ct - P+m-3 . (1.24)
Рассмотрим частные случаи результатов теорем 1.1-1.3. Если p(s) = (1 + s) l , s ^ 0, 0 C l < p, то согласно результатам теорем 1.1-1.3
q + m + 2 + —— := q*. (1.25) N l (q^-qXN-l) __ (q*-q)(N-l) __ q-(p+m-2) Тогда Ф(R) ~ R q-(p+m-2) , E(t) C YR(t) q-(p+m-2) , где R(t) ~ t (p-l)(q-(p+m-2))+p+m-3, при q = q* : E(t) C Y(lnt)-q,t > 1. Если же q> q* то E(t) > y, t> 1. Таким образом, ql∗в (1.25) играет роль критического показателя для задачи (1.1), (1.2). Всюду в дальнейшем параметрами γ, C , c, будем обозначать различные постоянные, которые зависят лишь от параметров задачи ^1, ^2, N, Р, m, q и не зависят от размеров области решения задачи. Работа организована следующим образом: в § 2 даются вспомогательные утверждения, §§ 3–7 посвящены доказательствам теорем 1.1–1.5 соответственно.
2. Вспомогательные утверждения В дальнейшем нам потребуются следующие леммы (см. [17]). Лемма 2.1. Пусть последовательность yh, h = 0,1, 2,..., неотрицательных чисел удовлетворяет рекуррентному соотношению yh+1 C Cbhy1+e, h = 0,1,..., с какими-либо положительными постоянными C, е и b ^ 1. Тогда yh ^ 0, h ^ то при 1 1 условии, что у о C C Еb ^2. Лемма 2.2. Пусть yn, n = 0,1, 2,... , — последовательность равномерно ограниченных положительных чисел, удовлетворяющих рекуррентным неравенствам yn < сьпуП+а, / 2C\ “ \ ь1-а / . где C, b > 1 и а € (0,1) — заданные постоянные. Тогда yg C Пусть ^(R) := RN(p+m-3)+pp(R)p+m-2. Лемма 2.3. Пусть suppug С Br0и выполнены условия теоремы 1.1. Тогда для любого t > 0 имеет место оценка z(t):=inf {r : u(-,t)=0, |x| > r} C 4Rg + y^( 1) (t|ugp|p+m 3). <1 Обозначим ri = RR - ^2R + R (a2 - ^1), ri’ = R + a J! - R (a2 - ax), где i = 0,1,..., R > 4R0, 4 > a2 > ax > 0. Пусть Ai = ri < |x| < ri’ C Ai+1. Рассмотрим срезающую функцию ni такую, что ni = 1, x € Ai, ni = 0 вне Ai+1, |Vni| С Y(2—iR(^2 - ap)-1. Возьмем в интегральном тождестве в роли тестирующей функции nip-iU8, где 9 > 0. Тогда, рассуждая также как в [18], получим неравенство sup 0 t j ,,u+n dx +H RN 0 RN t um^6-‘2lVu\PnPidxdT + j J uq+8np dxdt 0 RN t С Y(2-iR(a2 - a1))-pj j up+m+8-2dxdT. (2.1) 0RN A supp ni p+m+6 — 2 Обозначим u p p(1+6) sp p sp(1+6) ns = Vi, s > 0, т. е. unip+m+O—2= vip+m+O—2. Значит, u1+8n"6- vp+m+9-того, - при условии, что s выбрано удовлетворяющим неравенству s(1+e) > p+m+8-2 > 1. Кроме С 2P-1^ p + m + 9 p I / p+m+6 — 2 \ ip |V(unS-1) I = |VVi|p -^)pnm+8-2|Vu|pnsp+ up+m+8-2sp|Vni|pns-p] С Yum+8-2ИЧ + Y [2-iR(a2 - -p p+m+8-2 sp u η. Таким образом, из неравенства (2.1) получаем, что t t Ji := sup 0 I pvia dx + j j |Vvi|pdxdT + j j npup+edxdT RN 0 RN 0 RN 2ip С Y------;—— (a2 - ai)pRp t j j vp+1 dxdT, 0 RN (2.2) где a = p+(m+,8—2 • Применяя неравенство Ниренберга — Гальярдо, получаем 1 p α p vip+1 dx RN < Y |Vvi+1|p dx RN j v+ dx RN 1 —a µ , (2.3) N (N-p)a . N(1-a) p где а определяется из условия -N = v p' + v ^ 7 ,ц = p+m+8-2, т. е. a = Возводя (2.3) в степень p и применяя неравенство Юнга, получаем N (p+m+9-3) N(p+m+8-3)+p" -Rp j vp+1 dx RN С £ j |Vvi+1|pdx + yR RN P 1 1-a 1+6 £ 1 α -α j vi+1^dx RN p µ . Интегрируя по времени обе части этого неравенства и замечая, что в силу условия H j v+ dx = j P(|x|)P(|x|) Ai+1 Ai+1 1v+ dx ^ YP(R) 1 j PVi+1dx, Ai+1 приходим к неравенству tt Rp j j Vi+1dxdT ^ e j j |Vvi+i|pdxdT 0 RN 0 RN α p +ye1-aR 1-at [p(R)] —p( sup 0<τ µp ρviµ+1dx . RN (2.4) Следовательно, объединяя (2.2) и (2.4), имеем α α Ji ^ EJi+1 + -•~R ~tp(R) p µ p (sup / pv^ dx . 0<τ RN Итерируя это неравенство, получим p Jo ^ yR- 1-a tp(R) p µ sup 0<τ j (pv^ dx) p . (2.5) RN Далее, применяя неравенство Г¨ельдера, с учетом H получаем θ Г 1 1+6 i \ 1+6 1 /\ sup pudx\ ^ sup pu1+ dx / p dx < J0+6 0<τ Ao J L Ao J \Ao / \Ao/ θ 1+e p p 1 — p 1 । 6 N6 Г f I m(1+6) < yR (1+6)(1-a) t1+6p(R) + 1+6 1+6R1+6 sup pudx\ 0<τ A∞ (2.6) . Заметим, что Ao — R^2^ — ^1 < |x| < R(1 + ai), A^ — R^21 — ^2) < |x| < R(1 + ^2). Выберем: a2 = 52 n, a = 52 n1, n = 0,1,..., 0 < 5 < 4. Тогда после элементарных упрощений и подсчета постоянных находим из (2.6), что Mn := sup 0<τ <1 pudx ^ Ybnt1+6R Bn N(p+m-3)+p p+m-2 1+ p+m-3 1+6 p(R) 1+6Mn-11+6, где Bn = R(2) — 52 n 1< |x| < R(1 + 52 n1). В силу итератированой леммы 2.1 выводим, что Mn ^ 0, n ^ то, если 1 N(p+m-3)+p p+m-2 p+m-3 Yt 1+6 R 1+ p(R) M0 1 + 6 можно ^(R) = 2Y1+e tMp+m-3E1 (1+e), или отсюда R = R(t) = ^(-1) (rtMp+m-3), где Mo = JRN puodx. ▻ Обозначим t Yn+1 := sup У pvn+1 dx + У У |Vvn+1|pdxdT An+1 0 An+i tt + / 1 Ппuq+e dxdT ^ Y-pR^ j j < dxdT, 0 An+1 0 RN (2.7) An = Rn< |x| < R", Rn= R У - CTR, R’ = R + а2 2n n nR, V ст : 0 < а< 4, p+m+9-2 где 9 > 0, b1 > 2, vn = up пП и ηn— срезающая функция An. Справедлива Лемма 2.4. В условиях предыдущей леммы имеет место неравенство (i+»)p 2np t ”+Ee? 1+ Yn + 1< Y —p(p+m+9-2)Yn CTRp(R) в+9р p(p+m- в+9р , где в = N (p + m - 3) + p. (2.8) <1 В силу неравенства Соболева — Ниренберга — Гальярдо vnp dx RN p < Y I / |Vvn|Pdx RN b p vnadx RN 1-b a . Здесь 0 < b (1+e)P b_ a = p+m+e-2, b = < 1 определяется из соотношения N (N-p)bp N(P+mP+3)+(1)+e)P. Далее, рассуждая как в лемме 2.3, + (1 b)N. Значит, a, получим t j j vn dxdT < y 0 RN t bt p a 1-b j j |Vvn|pdxdT I I У I У va dx I dT 0 RN 0 RN tb Р (1-b) p(r)-a(1-b) / / |Vvn|pdxdT I t1-bsup / pvn dx J J / 0 0RN RN < Yt1-bp(R)-p(1-b)Ynb+a(1-b). Теперь, если воспользоваться аналогичным (2.1) неравенством, придем к требуемому утверждению. >
3. Доказательство теоремы 1.1
Имеем
E(t) : =j p(|x|)u(x,t) dx = j p(|x|)u(x,t) dx + j p(|x|)u(x,t) dx := I1(R) + I2(R).
(3.1)
RN
BR
|x|>R
Применяя неравенство Г¨ельдера, получим
q-1
Ii(R) ^
(3.2)
BR
В силу леммы 2.4 и неравенства (1.6) имеем
/ q dx < ^-1 у ■ t dx
BR
BR
BR
^ ^11 У g(x, t, u) dx = —^11
RN
dE dt .
(3.3)
Следовательно, из (3.1)–(3.3) выводим E(t)< Д1 1 q q-1 q (- _) ,1(R)Th№ (3.4) где ^1(R) := Jbr p(|x|) q-1dx. В силу условия H ^1(R) ~ RNp(R) q-1. Для оценки I2(R) поступим следующим образом. Пусть Ri = R(1+2-i), i = 0,1, 2,... Пусть Z(x) — гладкая функция на (0, то) и такая, что Z(x) = 1 для |x| ^ Ri, Z(x) = 0 для |x| < Ri+1, 0 < Z(x) ^ 1 для Ri+i < |x| < Ri. Обозначим Ui = |x| > Ri. Умножим теперь обе части (1.1) на Zs(x) и результат проинтегрируем по RN х [0,t). Это даст t /z waxing) dx + / /g(x,i,u)z-(x) -х-т RN — t / «^s-1]T a.(x 0 RN i=1 0 RN ,t,u, Vu)ZXi dx-т + У Zs(x)p(|x|)uo(x) dx. RN В силу (1.4), (1.5) отсюда получаем, что t j Zspudx + Ц1 j j uq Zs dxdT RN 0 RN t ^ «ц2 J J um-1|Vu|p-1|VZ|Zs-1dx-т + jzspu0dx. (3.5) 0 RN RN Обозначив первый интеграл справа через e(R,t), оценим его по неравенству Гельдера E(R,t) < I I 0 RN ∩ supp ∇ζ тeum-1-) | Vu|pzs dxdT х -1 p t J Jт-e(p-1)zs-p|Vz|pu(x,t)dx* 0 RN p p-1 1 = I3 p 14, (3.6) где 0 < в < p--i, 9 = 2p—m. Заметим, что в силу условия H имеет место неравенство t I4 ^ suP ТТйй XEB2R\Brp(|x|) у у т-e(p-1\s-pivzippu 0 RN < ct1 1) (R1 PPsup[ Pu(x,T) dx- (3.7) p(R)Rp0 Ui+1 Далее, для оценки I3 умножим обе части (1.1) на τβu1-θζsи результат проинтегрируем по частям по RN x (0,t). С учетом (1.3)-(1.5) и неравенства Юнга, это даст t ^m 0 RN < t 9// 0 RN t тeum-1-Zsdxdт + ^1 У У тeuq+1^e|Vu|PZsdxdт 0 RN t (3.8) тe-1pu2-6ZsdxdT + R 2ipУ У тeum ■ p-'Zs-pdxdт =: I5 + I6. 0 RN В силу неравенства Юнга имеем tt I5< E1 j У тeuq+1-eZsdxdт + C(E1) У У тd q-θ q-θ q-1 pq-1 (|x|)uZs dxdт- Заметим, что второй интеграл в правой части (п. ч.) этого неравенства оценится ющим образом: следу- п. ч. ^ Ct1+e q—e 1—9 q-1p(R) q-1sup 0<τ uρζsdx. (3-9) RN Далее имеем по неравенству Юнга t 'б < Ei ft 0 RN тeuq+1-6ZsdxdT + C(e1)2 q-p+m-2) t1+eRN —p(q+1-9) R q-(p+m-2) . (3.10) Таким образом, из (3.8)-(3.10) выводим при достаточно малом E1 > 0 tt j j тeum-1-e|Vu|PZsdxdт + У j тeuq+1-Zsdxdт < Ct1+e-?-1p(R) q-1sup [ Zsupdx + cb'iRN 0<τ p(q+1-e) 1 д q- (p+m-2) t1+e где b > 1. Обозначив sup 0<τ / pu dx = Ii+1, Ui+1 (3.11) 1 —e(p-1) , —1 t1 pR p(R) p = B1(R, t), (-i । _q — 6 A (p— 1A 1 — 0 p— 1 tl1 " q-1) I p P pR)) q-1P = B2(R, t), (p—I)(q+1—6) 1+e N(p—1) R q—(p+m —2) t — R -^T- = B3(R,t) и объеденив (3.6)–(3.11), получим .—1 p ) 1 + biB3(R,t) (3.12) E(R,t) С 7Bi(R,t)< B2(R,t) sup У Zsupdx 0<τ Оценим (3.12) по неравенству Юнга следующим образом: e(R, t) С e2 sup 0<τ -p pudx + yR p—1P ; J Ui+1 q—(p+m —2) (p—1)(q—1) sup 0<τ ζsρudx RN p + bit p—1R N- q—(p+m —2) p qp—1 L_ Г t 1 (p—1)(q—1) p—1 q—(p+m —2)p(R) p—1= £2pi + i(t) + Y -------- p(q— 1) Lp(K)Rq—(p+m—2) J (3.13) x sup 0<τ / Zsup dx + Ybi ; J RN t p(q—1) p(R)Rq—(p+m—2) p(R)RN p. R q—(p+m —2) Имеем E(R,t) С YBi(R,t)B: p—1 r 2p(R,t) sup / Zsupdx 0<τ 0<τ RN -1 p—1 p 1 p Ii+1 + YbiBi(R,t)B3(R,t)Ii+i p С Ep—1 P p [sup [ Z supdx \ + E_P 0<τ RN p - 1 г p P [Bi(R,t)B2p(R,t p Ii+1 + 2 1 T F P — Ii+i+^2 p2 ~ Ii+i+^2 p2 p—T P - 1 p pp bip—1 [Bi(R,t)B2(R,t)J p—1. p—1 Вычисляя [Bi(R,t)B2p (R, t)]PEiPp = 6, p п.ч. < 6Ii+i + E2(6) — p pp bip—1 [Bi(R,t)B2(R,t)J p—1, p Ii С 5Ii+i + bii [Bi(R, t)B2(R, t)] p—1, выбирая 6 настолько малым, что 6bi < 1. Здесь pi := supo для сколь угодно малого 6(Г) выполняется y6 (p—1)(q—1) < 4. Наконец, из (3.4) и (3.13) выводим f r j p(R)RN . pi(t) dx С y uopdx + dpi+i(t) + Yb2 =— p R(t) q—(p+m—2) |x|>R(t) Итерируя это неравенство при достаточно малом E2 > 0, получим оценку P0(t)< Yi u0ρ dx |x|>R(t) , p(R)RN + Y2 =-- p R(t) q—(p+m—2) := E2(t). Таким образом, I2(R) С E2(t). Значит, из (3.4) имеем для 0 < т < t F(т) = Е(т) - E2(t) С дГ1^ — dF^) 4 RN(t)p(R(t) q-11 - Интегрируя это неравенство от 0 до t, приходим к требуемому утверждению. Теорема 1.1 доказана.
4. Доказательство теоремы 1.2
Из (1.1) имеем
d
— pu(x, t) dx =
RN
- j g(x, t, u) dx.
RN
(4.1)
Применяя неравенство Г¨ельдера и (4.1), получаем i q - i i q - i J Hx-t)dx g(x, t, u) dx BR BR BR BR BR С I — ^i1dt у pu(x,t) dxj (у BR BR q-1 (4.2) Так как носитель начальной функции содержится в шаре Br0, то согласно лемме 2.3 носитель u(x,t) также содержится в шаре радиуса R(t) = 4Ro + Y^(t). Следовательно, R q-1 С CnR(t)N(q-1)p(R(t))q. (4-3) N-q Поскольку по условию теоремы Ci С p(R)R q (p- m 2) С C2 для всех достаточно больших R > Ri, то по определению R(t) получим, что при достаточно больших t > ti(Ro, ||uop|i) RN(q-i)p(R)q~ t. (4.4) Таким образом, из (4.2), (4.3), (4.4) находим d dt J pu^x.t) dx ^ Yti У pu(x, t) dx^ . Интегрируя это неравенство в промежутке [ti,t], приходим к требуемому утверждению. Теорема 1.2 доказана.
5. Доказательство теоремы 1.3 Прежде всего отметим, что если p(|x|) ~ |x| l, 0 С l < p, и suppuo C Br0(0), Ro < то, то для всех t > 0 имеют место оценки [1] p-N-l (5.1) u(t) х С Chpuohilt hl , suPP u(x,t) G BR(t)(0), (5.2) p+m-3 1 где Z(t) = 4Ro + Yllpuo II h th , h = (N — l)(p + m — 3) + P — l > 0. Следовательно, интегрируя (1.1) по Q(ti, t2) = RN x (ti, t2), ti < t2, получаем E(ti) := / RN pu(x, t1) dx t2 = p™ RN t1 RN g(x, t, u) dxdT < t2 E(t2) + ^2jj t1 RN uq(x, т) dxdT. (5.3) Учитывая оценки (5.1), (5.2), отсюда имеем t2 jf u (x,T) t1 RN t2 dxdT ^ y J" ||u(TW^-RC7)l t1 dT x E(t ) dT t2 /p(q-1) / p+m-3 ^\ E(0) hi MRo + yE(0) hi т hi }E(t) dT t1 < YE(ti)E(0) p(q-1) । (p+m-3)l hl hl t2 / t1 τ (N-l)(q-1) l hl τ hl dτ (5.4) (p+m-3)l -L. при условии, что ti выбрано настолько большим, что 2Ro ^ yE(0) hi ti1. Тогда в силу того, что q > ql∗ ∞ Г _ (N-i)(q-1)-i t hi dT < то. t1 Следовательно, из (5.4) получаем, что (■ Г _ (N i)(q q*) p(q-1) + (p+m-3)i uq(x,T) dxdT < Yt1 i E(0) hi E(t1). t1 RN Окончательно из (5.3) и (5.5) находим _ (N-Kq-T) p(q-1) + (p+m-3)i E(ti) < E(t2) + Yt1 hi E(0) hi E(ti). Теперь, выбирая t1 достаточно большим, имеем _ (N i)(q q*) p(q-1) + (p+m-3)i Yti -i E(0) hi = - а из (5.6) поучаем, что E(t2) > YE(t*). (5.7) Осталось показать, что E(t*) > 0. Лемма 5.1. Решение (1.1) не может удовлетворять условию u(x,to) = 0, Vx € RN и V to > 0. <1 Доказывается точно также как в работах [2, 4]. > Теорема 1.3 доказана.
6. Доказательство теоремы 1.4 Итак, пусть q = p + m — 2. Нам потребуется следующая лемма Стампаккия. Лемма 6.1. Пусть ^(s) — неубывающая неотрицательная функция, определяемая на [ko, то], и такая, что для всех l > k ^ ko выполняется ^(l)< (rCy *W' (6-1) где C и т — положительные постоянные. Тогда для любого k > ko имеет место оценка ^(k) С v(ko) exp [1 — (Ce)-T(k - ko)] - (6-2) В силу леммы 2.4 t Yn+1 : = sup o 1+dx+/ / uQ+m-2 |Vu|p ДхДт An+1 o An+i t +и o An+1 u6+m 2dxdT С y (i+»)p i+ m1 p bn t Yn e+p6 p(p+m+9-2) RPp(R)-в+9р (6.3) и, следовательно, Yn ^ 0 при условии, что (p+m-3)p_ (1+g)p p(p+m+6-2) Y1 e+p6 t"Fw R-Pp(R) e+p c e, где ε — достаточно малое положительное число, зависящее лишь от параметров задачи. Предыдущее неравенство эквивалентно неравенству Yp+m 3 t1+6R-(e+p9)p(R)-(p+m+9-2) ^ £в+pP . (6-4) Пусть t V(R) := j j uP+m-<2+dxdT. o|x|>R Тогда легко получаем неравенство ^(R) С yRp^(RR)■ Взяв теперь в лемме l = R, k = RR, т = p, C = y, получаем, что ϕ t (3R) - I I Lo RN up+m+S-2dxdT exp(—yR)- Далее заметив, что pug G Li+e, имеем 1 1+0 t f pu^+dx + +1// RN 0 RN t Um+e-2 |Vu|pdXdT + +1 У У Up+m+e-2dXdT 5 0 RN 1 1+0 ; jPu0+edx. RN Следовательно, ϕ exp(-yR). RN Таким образом, (6.4) удовлетворится, если p+m-3 t1+e exp ( - Y(p + m - 3)R)R-(e+pe)p(R)-(p+m+e-2)5 Ei, (6.5) RN где Ei достаточно мало. Очевидно, что (6.5) будет выполнено, если для достаточно больших t > 0 выбрать R следующим образом: R ^ R(t) : = Гlogt, где Г = Г(||идp^i+e, Ei) — достаточно большая константа. Тогда мы приходим к замечанию, что и = 0 вне шара Briog t. Для доказательства теоремы осталось оценить массу решения для достаточно больших t. В силу неравенства Г¨ельдера / '■5 (-dx RN RN 1 1+θ ρ dx θ 1+θ . (6.6) Следовательно, оценка массы сводится к оценке интеграла E1+e(t) := У pu1+edx. RN Интегрируя (1.1) по RN легко получить неравенство d1 pu1+edx 5 RN -Y У up+m+e-2dx. RN (6.7) Применяя неравенство Г¨ельдера, получаем j pu1+edx 5 RN 1+θ p+m+θ-2 j up+m+)-2dx\ RN p+m-3 p+m+θ-2 , (6.8) где D(T) = T dd-tEi+e(t) 5 -yD(T) p+m+θ-2 D+m-3p+m+θ-2 1+Ei+e+ (t), 0 (6.9) p p+m—3 (x)dx. Интегрируя (6.9) в пределах от 0 до T, получаем, что 1+θ Ei+e (T) 5 YT p+m-3 D(T). Наконец, объединяя это неравенство с (6.6), получаем j pu(x, T) dx ^ y RN θ ( / Pdx) 1+’ Br log T T p+m — 3 (/ Br log T p+m+6 — 2 P p+m — 3 1 )i+e p+m —2 M1 = ypp+m—3(log T)(logT)NT p+m—з. Теорема 1.4 доказана.
7. Доказательство теоремы 1.5 Из неравенства (2.7) следует, что t t где a = Yp+1 := sup 0 j Pvp+idx + j j \^vn+1\pdxdT + j j vV+1dxdT An+i 0 An+i 0 An+i (1+S)p p+m+в-2 , (q+9)p p+m+8-2. t < Y ^P- [ vP dxdT, σpRp n , 0 RN (7.1) Далее, условие q < p + m — 2 позволяет применить тройное мультипликативное неравенство типа Соболева — Ниренберга — Гальярдо. Для получения этого неравенства поступим следующим образом: j vP dx< Y RN (1 —B)p b (7.2) где B определяется из соображения размерности N JN—PB + N(1 — B)ia = (1 + .)p ,v = P(q + «) . p p b p + m + 6 — 2 p + m + 6 — 2 Применяя неравенство Г¨ельдера, имеем j vn dx < RN ν-a ν-a b-a (7.3) Соединяя неравенства (7.2) и (7.3), получаем B ν - b j vPdx< Y RN |∇vn|pdx vnνdx RN RN ν a - ν-a ν-b (1—B)p b (7.4) Теперь подберем параметр b так, что B+ (1 — B)p (v — b) b = 1. ν-a (7.5) t t t j j vndxdT ^ y 0 RN j j \^vn\PdxdTt j j vndxdT 0 RN 0 RN v-b (1-B)p x sup / pvndx \ 0 RN ν-a b p(R) v-b (1-B)p ν-a b . (7.6) Следовательно, из (7.1) и (7.6) вытекает Y2np , - b—a (1 — B)P1+ — Yn+1 < / p(R)v-a bYn va , Yn ^ 0 при n ^ to. (^R )p Вычисления дают ν-b ν-a < E1- Rpρ ν-a (7.7) Пользуясь условиями H, легко проверить, что R-pp-ba4Bp(r) ^ yR-pp(R)< yR-^p-ct), ^ Следовательно, (7.7) выполнено, если т. е. R-.^P-^ ν-b ν-a £1 2 , 2y* £1 ν-b p-σ u(x, t) = 0 вне шара радиуса R = 4Ro + R j pudx < RN uqdx q ρ q- q-1 q q j uqdx ^ y RN RN Интегрируя уравнение (1.1) по RNи учитывая (1.5), получаем ddt ^udx ^ —^1 1 uqdx< —№Y I q ρu dx RN RN RN Интегрируя это неравенство, имеем dE -µ1γ dt, ^ Eq ^ E1-q(0)) ^ —^iYt. q <E1-q(t) - Отсюда следует, что при t > 0 E(t) < Yt-q-1, что и требовалось доказать. Теорема 1.5 доказана.
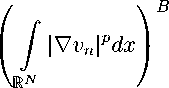
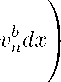
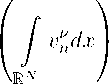
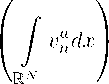
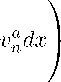
Вычисления дают
N (p - b) Pv
B = —7----\----, b = --------
N (p — b) + bp P — a + v
Замечая, что
У vndx < yp(R)-1 У pvndx
RN RN
и интегрируя по времени (7.4) с учетом (7.5), получаем
t
Y1 = sup / pu1+6 dx + 0
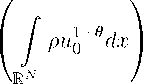
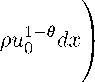
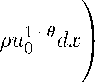
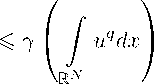
Список литературы Скорость убывания массы решения задачи Коши дважды нелинейного параболического уравнения с абсорбцией
- Tedeev A. F. The interface blow-up phenomenon and local estimates for doubly degenerate parabolic equations // Appl. Anal. 2007. Vol. 86, № 6. P. 755-782. DOI: 10.1080/00036810701435711
- Andreucci D., Tedeev A. F., Ughi M. The Cauchy problem for degenerate parabolic equations with source and damping // Ukr. Math. Bull. 2004. Vol. 1, № 1. P. 1-23.
- Ben-Artzi B., Koch H. Decay of mass for a semilinear parabolic equation // Commun. Partial Differ. Equ. 1999. Vol. 24, № 5-6. P. 869-881. DOI: 10.1080/03605309908821450
- Skrypnik I., Tedeev A. F. Decay of the mass of the solution to Cauchy problem of the degenerate parabolic equation with nonlinear potential // Complex Var. Elliptic Equ. 2018. Vol. 63, № 1. P. 90-115. DOI: 10.1080/17476933.2017.1286331
- Kamin S., Rosenau P. Propagation of thermal waves in an inhomogeneous medium // Commun. Pure Appl. Math. 1981. Vol. 34, № 6. P. 831-852. DOI: 10.1002/cpa.3160340605
- Kamin S., Rosenau P. Nonlinear diffusion in finite mass medium // Commun. Pure Appl. Math. 1982. Vol. 35, № 1. P. 113-127.
- DOI: 10.1002/cpa.3160350106
- Kamin S., Kersner R. Disappearance of interfaces in finite time // Mechanica. 1993. Vol. 28, № 2. P. 117-120.
- DOI: 10.1007/BF01020323
- Eidus D., Kamin S. The filtration equation in class of functions decreasing at infinity // Proc. Amer. Math. Soc. 1994. Vol. 120, № 3. P. 825-830.
- DOI: 10.1090/S0002-9939-1994-1169025-2
- Galaktionov V. A., Kamin S., Kersner R., Vazquez J. L. Intermediate asymptotics for inhomogeneous nonlinear heat conduction // J. Math. Sci. 2004. Vol. 120, № 3. P. 1277-1294. DOI: 10.1023/B:JOTH.0000016049.94192.aa.
- Guedda M., Hihorst D., Peletier M. A. Disappearing interfaces in nonlinear diffussion // Adv. Math. Sci. Appl. 1997. Vol. 7, № 2. P. 695-710.
- Мартыненко А. В., Тедеев А. Ф. Задача Коши для квазилинейного параболического уравнения с источником и неоднородной плотностью // Журн. вычисл. матем. и мат. физики. 2007. Т. 47, № 2. С. 245-255.
- Мартыненко А. В., Тедеев А. Ф. О поведении решений задачи Коши для вырождающегося параболического уравнения с неоднородной плотностью и источником // Журн. вычисл. матем. и мат. физики. 2008. Т. 48, № 7. С. 1214-1229.
- Reyes G., Vazquez J. L. The inhomogeneous PME in several space dimensions. existence and uniqueness of finite energy solutions // Commun. Pure Appl. Anal. 2008. Vol. 7, № 6. P. 1275-1294.
- DOI: 10.3934/cpaa.2008.7.1275
- Reyes G., Vazquez J. L. Long time behavior for the inhomogeneous PMI in a medium with slowly decaying density // Commun. Pure Appl. Anal. 2009 Vol. 8, № 2. P. 493-508.
- DOI: 10.3934/cpaa.2009.8.493
- Kamin S., Reyes G., Vazquez J. L. Long time behavior for the inhomogeneous PME in a medium with rapidly decaying density // Discrete Contin. Dyn. Syst.-A. 2010. Vol. 26, № 2. P. 521-549.
- DOI: 10.3934/dcdc.2010.26.521
- Benachour S., Laurentcot Ph. Global Solutions to viscous Hamilton-Jacobi equations with irregular initial data // Commun. Partial Differ. Equ. 1999. Vol. 24, № 11-12. P.1999-2021.
- DOI: 10.1080/03605309908821492
- Di Benedetto E. Degenerate parabolic equations. New York: Springer-Verlag, 1993. 387 p.
- Andreucci D., Tedeev A. F. Universal bounds at the blow-up time for nonlinear parabolic equations // Adv. Differ. Equ. 2005. Vol. 10, № 1. P. 89-120.


