Случайное и закономерное изменение цены акции в зависимости от длины временного интервала

Теоретическая основа исследования и предшествующие исследования

В основу проведенного исследования легли, с одной стороны, теории случайного блуждания цен, а с другой стороны, наличие закономерности роста цен акций на фондовом рынке за более-менее продолжительные промежутки времени, что в обобщенном виде проявляется в росте фондовых индексов, несмотря на все известные в истории кризисные события на данном рынке и в экономике в целом.

Вопросы случайности в динамике цен акций постоянно находятся в центре вни- мания теоретиков и практиков фондового рынка. К настоящему времени написано большое количество статей по самым разным аспектам случайной природы цены акции, основу которых составляют работы М. Кендалла [16], П. Самуэльсона [21], Ю. Фамы [12,13], У. Шарпа и других исследователей. Почему-то считается, что теоретические изыскания по данному вопросу ведут свое начало от известной работы Луи Башелье [8], что не совсем корректно в силу двух обстоятельств.

Во-первых, эта работа Луи Башелье была написана в самом начале ХХ века, но забыта на полвека и стала известной («об- наруженной») лишь в 50-х годах. В силу этого нельзя утверждать, что исследование проблемы случайного характера цены акции началось именно с данного автора.

Во-вторых, о случайной природе цены акции было известно экономистам и до Ба-шелье (см., например, [20]). Даже Маркс, задолго до Башелье, писал, что цене акции присущ случайный характер, и это не было его собственным открытием, т.к. он в данном случае просто обобщал то, что уже было известно экономистам-исследователям и в XIX веке. «Рыночная стоимость этих бумаг отчасти спекулятивна, т.к. определяется не только действительным доходом, но и ожидаемым, заранее исчисленным» [6, с. 10].

Но для нашего исследования данная позиция важна еще и тем, что в ней четко прослеживается подход к изменчивости цены акции во времени, который носит вовсе не чисто случайный характер, как это обычно видится со стороны участников рынка и вышеобозначенных экономистов-теоретиков. Данный подход означает, что в изменении цены акции следует видеть единство ее и случайного и неслучайного (закономерного) изменений.

Такое же понимание характера изменения цены акции было и у последователей учения Маркса. Например, Р. Гильфердинг в его известном произведении «Финансовый капитал», изданном в 1910 году (а книга была написана в основном к 1905 г.), также неоднократно отмечал: «… Так и для курсов (-акций), наряду с собственно определяющими цены моментами, следует различать те случайные моменты, которые выражаются в изменяющемся соотношении спроса и предложения» [7, с. 190].

Поскольку такой подход к рассмотрению цены акции обычно отсутствует, то можно сказать, что, по сути, отсутствуют и статьи, в которых затрагивалась бы про- блема поиска количественного соотношения случайной и закономерной сторон изменения цены акции. Можно обоснованно предположить, что это соотношение должно быть различным на временных интервалах, существенно различающихся между собой по длительности.

В работах российских авторов (Алехин [1], Берзон [2] и др.) обычно указывается на то, что динамика цены акции характеризуется наличием и случайных колебаний, и тенденции к ее росту, но ни о каких подходах к выявлению их соотношения между собой не говорится. Кроме того, следует заметить, что закономерное в движении цены акции обычно понимается только как тенденция к росту цены, хотя, рассуждая логически, тенденция к снижению цены столь же возможна, как и тенденция к ее росту. Например, относительное ухудшение положения компании на рынке, которое может продолжаться многие годы, неизбежно ведет к соответствующей динамике рыночной цены ее акций.

В то же время в работах, посвященных моделям цены акции, упор делается на математическое описание случайного процесса изменения цены, причем понимается под этим не случайность вообще, а «закономерная случайность» в виде следования колебаний цены акции закону нормального, а точнее – логнормального, распределения вероятностей. Здесь сама вероятностная случайность принимает форму особого рода закономерности, получая математический вид винеровского процесса и процесса Ито. Логнормальное распределение есть всегда односторонняя закономерность, т.е. закономерность одного направления – роста цены акции. Но для разных временных интервалов законом может быть как рост цены акции, так и ее снижение. Кроме того, в математических моделях «закономерность» находит выражение еще и в на- личии констант, прямо не связанных с дисперсией, но опосредованно зависящих от нее через общий (единый) механизм расчетов модели цены акции. В целом следует отметить, что ни логнормальность распределения вероятностей, ни константы, в силу их «неизменности», при любых их «совершенствованиях» не позволяют выявить изменение роли случайной и закономерной составляющих применительно к разным временным интервалам колеблющейся во времени цене акции.

Тенденция к росту или снижению цены акции коренится в том, что акция есть форма, в которой капитал существует в сфере обращения в качестве товара. Цель любого капитала – получение наибольшей прибыли. За счет этой прибыли капитал постоянно возрастает, но в силу изменения спроса на создаваемые им товары размер функционирующего капитала не только возрастает, но и время от времени может сокращаться. Поэтому законом динамики цены акции, в большинстве случаев, является ее бесконечный рост, но только в форме постоянных ее случайных движений (колебаний) то вверх, то вниз от своего предыдущего уровня.

Под случайностью будем понимать изменчивость, будущий результат которой неизвестен. В этом случае сама изменчивость есть случайная изменчивость. Поэтому корректно утверждение, что цены акций изменяются случайным образом, т.е. никто не знает (или нет закона), какой будет по своей денежной величине цена акции в следующий или какой-то иной будущий момент времени.

Результат изменения какого-либо объекта может быть заранее известен или неизвестен. Известность будущего события обычно имеет место, если имеется (известен человеку) закон изменения объекта или если это событие есть результат целе направленной деятельности человека. Первое характерно для многих явлений природы. Например, закон тяготения управляет движением Земли вокруг Солнца, и потому ее будущее местоположение может быть определено заранее. Второе характерно, когда человек, применяя законы природы, создает из имеющегося вещества природы нужные ему вещи. Созданная вещь сначала существовала только в качестве мысленной абстракции, или цели, но затем она воплотилась в материальное благо. Каждый произведенный товар – это изменение вещества природы, результат которого был известен еще до того, как совершился процесс его производства.

Изменчивость цены – это непостоянство ее значений во времени. Как и цена любого товара, рыночная цена акции изменчива, но эти ее изменения заранее обычно неизвестны. Количественные размеры цены акции в разные моменты времени различаются, хотя иногда могут и совпадать. Изменчивость цены акции есть причина существования приростной доходности, или положительной разницы в ценах, но она же есть и основа возможной убыточности от купли-продажи акции, что совершенно нежелательно участнику рынка. Поэтому очевидно субъективное желание последнего как-то избежать негативного результата в будущем, что заставляет более глубоко исследовать само явление изменения цены акции.

Существуют два типа изменения цены акции: изменение как движение цены вверх или вниз и изменение цены как отличие предыдущего ее значения от следующего.

Первый тип изменения – это случайность в единстве с закономерностью. При этом случайность каждого из этих двух видов изменений имеет либо вероятность, равную 0,5, или одно из изменений имеет большую вероятность, что означает наличие тенденции изменения цены вверх или вниз. В случае цены акции существует тенденция к росту цены, а потому вероятность роста цены акции выше, чем вероятность ее снижения.

Второй тип изменения – это случайность без вероятности или, когда случайность любого возможного изменения имеет ограниченную вероятность, существенно меньшую, чем 0,5. Случайность без вероятности аналогична бесконечно малой вероятности того, что шар коснется поверхности в данной его точке, т.е. в пределе такая вероятность равна нулю.

Однако на организованном рынке цена акции меняется только кратно определенному шагу, размер которого устанавливается биржей. Поэтому каждое следующее возможное значение цены для единичной сделки известно, т.к. составляет собой текущую цену плюс или минус шаг изменения цены. Но с учетом количественного несовпадения лотов на покупку и на продажу или при большом количестве сделок в единицу времени сам средний шаг, т.е. среднее изменение цены от сделки к сделке, превращается в случайную величину. В этом смысле случайность изменения цены акции есть результат случайно складывающегося множества проделанных «шагов».

Таким образом, с любой стороны рассмотрения изменения цены акции это изменение есть всегда единство случайности и закономерности. Выражаясь философски, следует сказать, что закономерно само изменение цены акции, а вот ее неизменность есть не что иное, как случайность отсутствия самого процесса ее изменения. С одной стороны, случайное событие – это всегда событие, уровень сложности понимания которого превышает уровень имеющихся научных знаний о нем. Случайно по отношению к человеку все то, что он не может объяснить. Поэтому углубление познания цены акции есть путь сокращения «сферы случайности», присущей этой цене. С другой стороны, случайность не существует в отрыве от закономерности. Цена акции случайна, но уже самая ее изменчивость – закономерна. Закономерно и самое общее направление изменения цены акции как внешней (рыночной, оборотной) формы существования капитала, непосредственно создающего прибыль. Поэтому логично предположить, что в случайных колебаниях цены акции есть «островки» закономерностей, а в любого рода закономерности, относящиеся к цене акции, «закономерно» встроены и определенные «отрезки» случайности.

Знание о существовании пропорциональности между случайной и закономерной составляющими цены акции может быть полезно для трейдеров (спекулянтов и инвесторов), осуществляющих свои торговые операции (стратегии) на разных временных горизонтах.

Гипотеза исследования состояла в следующем: по мере увеличения размеров временного интервала доля случайного фактора в цене акции уменьшается, а доля закономерного фактора возрастает.

Для целей данного исследования под случайным изменением цены акции понимается ее изменение, которое выходит за уровень, принимаемый за норматив ее закономерного изменения. В качестве норматива закономерного изменения использовалось изменение цены акции за данный временной интервал, рассчитываемое на основе изменения цены акции за год в целом.

Выбранными временными интервалами являлись: день, неделя, месяц, квартал, полугодие и один год.

Таблица 1. Расчёт норматива закономерного изменения цены по видам акций применительно к каждому временному интервалу

Вид акции	Изменение цены акции за 2013 год (цена закрытия 31.12.13 – цена открытия 02.01.13 (по модулю))	Изменение цены акции за день (гр.3) = (гр.2) / 360 дней	Изменение цены акции за неделю (гр.4) = (гр.2) / 52 недели	Изменение цены акции за месяц (гр.5) = (гр.2) /12 месяцев	Изменение цены акции за квартал (гр.6) = (гр.2) /4 квартала	Изменение цены акции за полугодие (гр.7) = (гр.2) / 2 полугодия
1	2	3	4	5	6	7
1. General Electric Co.	6,52	0,018111	0,125385	0,5433333	1,63	3,26
2. Walt Disney	25,6	0,071111	0,492308	2,1333333	6,4	12,8
3. Pepsi Co Inc.	13,76	0,038222	0,264615	1,1466667	3,44	6,88
4. Procter & Gamble Co.	12,76	0,035444	0,245385	1,0633333	3,19	6,38
5. Exxon Mobil Corp.	13,41	0,03725	0,257885	1,1175	3,3525	6,705
6. IBM	6,52	0,018111	0,125385	0,5433333	1,63	3,26
7. McDonalds Corp.	7,63	0,021194	0,146731	0,6358333	1,9075	3,815
8. Johnson & Johnson	20,57	0,057139	0,395577	1,7141667	5,1425	10,285
9. JPMorgan Chase & Co.	13,5	0,0375	0,259615	1,125	3,375	6,75
10. Deutsche Bank AG	2,6	0,007222	0,05	0,2166667	0,65	1,3

Изменения цены анализировались за более-менее бескризисный 2013 год. По каждой акции из имеющейся отчетности (база данных Macrobond) были рассчитаны фактические отклонения ее цены от «норматива» для каждого выбранного временного интервала. Расчет значений этого норматива для каждого вида акций приведен в табл. 1.

Итоги расчетов сгруппированы в несколько таблиц, по которым можно достаточно наглядно увидеть весь ход рассуждений, позволяющий на основе последовательности расчетных шагов сделать некоторые качественные выводы относи- тельно выявления в колебательных изменениях цены акции не только случайного, но и закономерного фактора. Это позволяет заключить, что, все-таки, в хаотичной динамике цены акции имеются и «поля» закономерности.

Краткое описание метода анализа

Для получения исходной информации было сделано: 30 случайных выборок для дневного интервала, 4 случайные выборки для недельного интервала, взяты все 12 месяцев, все четыре квартальных интервала и оба полугодия (шестимесячные интервалы).

Значения цен каждой акции сравнивались с «нормативом» и отклонения суммировались по их модулю.

Результаты уровней случайного изменения цен для каждого временного интервала определялись по всем выбранным 10 акциям и затем усреднялись по каждому временному интервалу.

Полученные результаты сравнивались по периодам времени, при этом уровень случайности за день был принят за 100%.

«Перекрестные» результаты проведенных расчетов приведены в табл. 2.

Как видно из таблицы, доля случайного фактора в цене акции снижается по мере увеличения временного интервала, но в разной мере. По сравнению с предыдущим интервалом случайный фактор всегда снижается на меньшую величину, чем его значение, когда различие составляет несколько временных интервалов от дневного интервала.

На основе данных табл. 2 (графа 2), т.е. по имеющимся точкам, был построен график изменения доли случайного фактора в цене акции в зависимости от длины временного интервала (рис. 1). На рис. 1 и по- следующих рисунках по оси ординат отражается доля случайного фактора в цене акции в процентах, а по оси абсцисс откладываются временные интервалы в днях.

На основе таблицы 2 и наглядного изображения ее результатов на рис. 1 можно сделать следующие предварительные выводы. Доля случайного фактора в изменении цены акции за недельный период составляет примерно 90%; доля случайного фактора в изменении цены акции за период в один месяц – примерно 79%; доля случайного фактора в изменении цены акции за квартал – примерно 73%; доля случайного фактора в изменении цены акции за полугодие составляет примерно 49%.

Таблица 2. Доля случайного фактора в цене акции и ее изменение по временным интервалам

Временной интервал	Усреднённая доля случайного фактора в изменении цены акций	Уменьшение случайного фактора по отношению к дневному интервалу	Уменьшение случайного фактора по отношению к недельному интервалу	Уменьшение случайного фактора по отношению к месячному интервалу	Уменьшение случайного фактора по отношению к квартальному интервалу
1	2	3	4	5	6
Дневной	100,00%	–	–	–	–
Недельный	90,18%	9,82%	–	–	–
Месячный	79,36%	20,64%	10,82%	–	–
Квартальный	73,30%	26,70%	16,88%	6,06%	–
Полугодовой	48,54%	51,46%	41,64%	30,82%	24,76%

Рис. 1. Изменение доли случайного фактора в цене акции

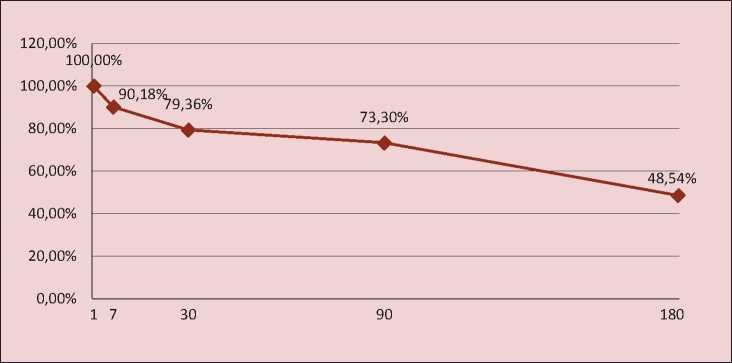
Таким образом, необходимо отметить, что наиболее существенное снижение доли случайного фактора в цене акции наблюдается не ранее полугодия. На наш взгляд, это связано с тем, что примерно за полугодие у компании уже имеется более достоверная (более надежная) и более полная (более «богатая») по сравнению с месяцем и кварталом отчетность о результатах ее деятельности. Обычно за это время уже явно вырисовывается увеличение (или уменьшение) функционирующего капитала компании. А ведь именно величина капитала компании и есть основа «закономерного» роста цены ее акции. В то же время, если речь идет о коротких промежутках времени, то применительно к ним изменение цены акции в наибольшей степени случайно. Это можно объяснить тем, что участники рынка за столь короткие сроки не могут «единодушно» оценить деятельность компании уже в силу того, что, с одной стороны, нет достаточной отчетности о работе компании, но главное – никто на рынке, даже сама компания, еще часто вообще не представляет, как она «сработала» за столь короткие промежутки времени.

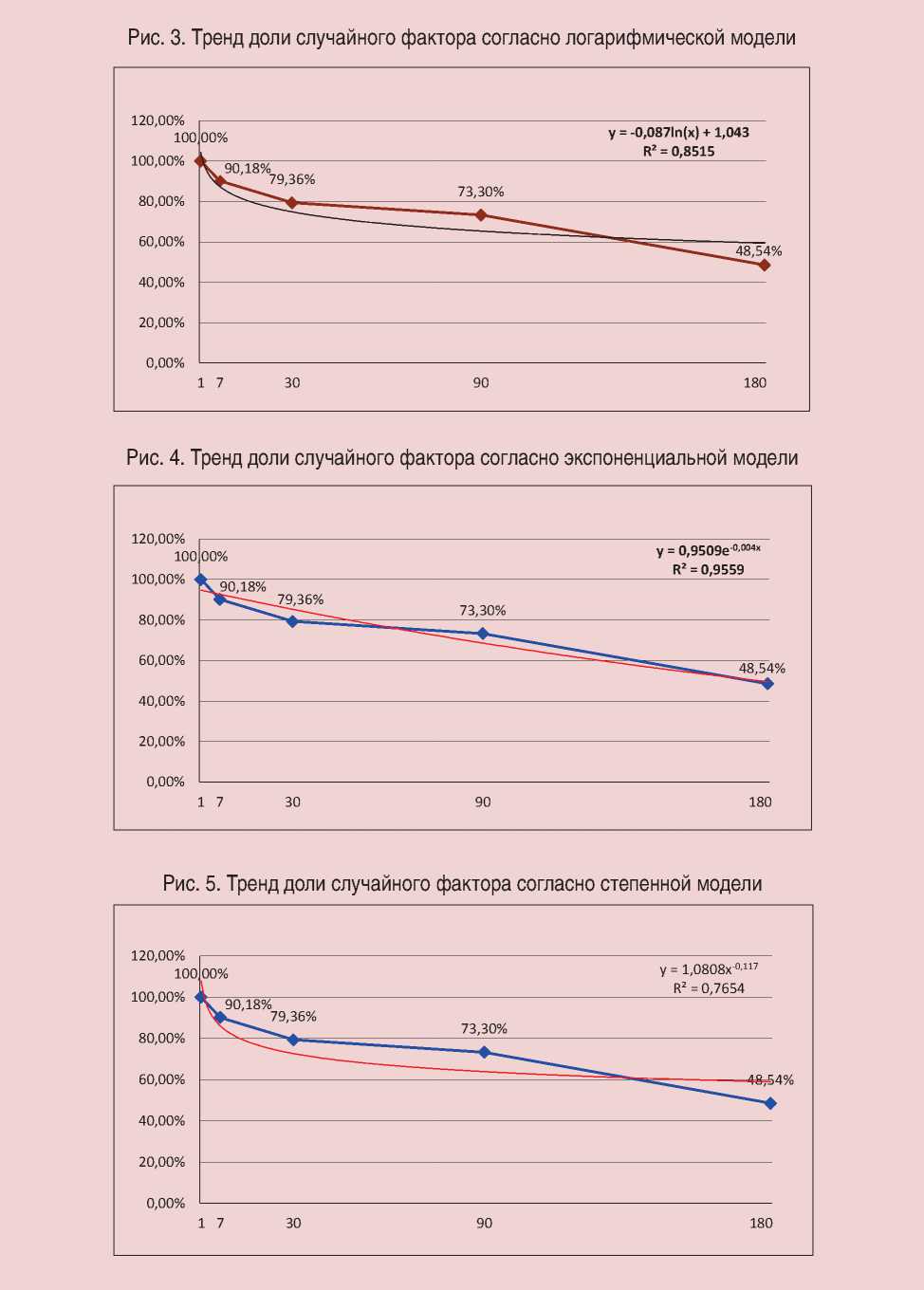
Следующим этапом анализа является расчет линии тренда путем построения разных по своей форме уравнений регрессии: рис. 2 – линейная регрессия, рис. 3 – логарифмическая зависимость, рис. 4 – экспоненциальная зависимость, рис. 5 – степенная зависимость.

Таким образом, согласно любой из примененных моделей регрессии, показывающих общий тренд, имеем:

• 1.    По мере увеличения размеров временного интервала доля случайного фактора в изменении цены акции уменьшается, а доля закономерного фактора возрастает.

• 2.    В пределах от месяца до трех месяцев (квартала) доля случайного фактора снижается существенно медленнее, чем это характерно для расширения временного интервала от квартала до полугодового интервала.

• 3.    В пределах от месяца до квартала доля случайного фактора снижается всего на шесть процентных пунктов против примерно двадцати пунктов снижения за период от одного дня до одного месяца. Такое резкое замедление снижения доли случайного фактора можно объяснить тем, что

  Рис. 2. Тренд доли случайного фактора согласно линейной модели

  
  
  

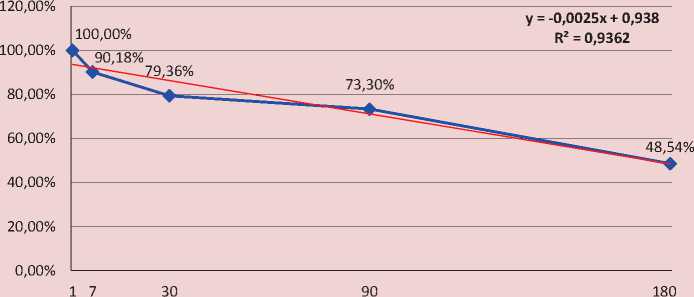
в период до месяца изменение цены уже «выбрало» весь «запас случайности», т.е. уже «испробованы» главные возможности колебаний («размаха») цены акции в условиях отсутствия результатов работы капитала за данный период времени. Дальнейшее увеличение временного интервала до квартала ничего не прибавляет к заложенной в цене акции «случайности», но еще не может и существенно уменьшить этот потенциал в силу того, что существенного прироста информации на рынке об экономической эффективности капитала акционерного общества еще нет.

Если проанализировать вышеприведенные модели с позиций их статистического «качества», то наилучшим образом фактическую динамику доли случайного фактора описывает экспоненциальная функция, т.к. у нее наиболее высокий показатель R² (табл. 3) .

Однако если попробовать продолжить по данным моделям расчеты доли случайного фактора за пределы года, то, как следует из табл. 4, начиная с некоторого временного интервала (в среднем уже через 1,5–2 года в зависимости от компании) изменение доли случайного фактора по раз-

Таблица 3. Сравнительные размеры показателя R2

Линейная функция	Логарифмическая функция	Экспоненциальная функция	Степенная функция
y = -0,0025x + 0,938	y = -0,087ln(x) + 1,043	y = 0,9509e-0,004x	y = 1,0808x-0,117
R2 = 0,9362	R2 = 0,8515	R2 = 0,9559	R2 = 0,7654

Таблица 4. Прогноз доли случайного фактора в изменении цены акции за пределы года

Годы Дни Степенная функция Линейная функция Экспоненциальная функция Логарифмическая функция x у у y у 1 1,08 0,94 0,95 1,04 7 0,86 0,92 0,92 0,87 30 0,73 0,86 0,84 0,75 90 0,64 0,71 0,66 0,65 0,5 180 0,59 0,49 0,46 0,59 1 360 0,54 0,04 0,23 0,53 1,5 540 0,52 -0,41 0,11 0,50 2 720 0,50 -0,86 0,05 0,47 2,5 900 0,49 -1,31 0,03 0,45 3 1080 0,48 -1,76 0,01 0,44 3,5 1260 0,47 -2,21 0,01 0,42 4 1440 0,46 -2,66 0,00 0,41 4,5 1620 0,46 -3,11 0,00 0,40 5 1800 0,45 -3,56 0,00 0,39 5,5 1980 0,44 -4,01 0,00 0,38 6 2160 0,44 -4,46 0,00 0,38 6,5 2340 0,44 -4,91 0,00 0,37 7 2520 0,43 -5,36 0,00 0,36 7,5 2700 0,43 -5,81 0,00 0,36 8 2880 0,43 -6,26 0,00 0,35 8,5 3060 0,42 -6,71 0,00 0,34 9 3240 0,42 -7,16 0,00 0,34 9,5 3420 0,42 -7,61 0,00 0,34 10 3600 0,41 -8,06 0,00 0,33 ным моделям не всегда принимает рациональные значения.

Данные таблицы показывают, что только по степенной функции и по логарифмической функции дальнейшее снижение доли случайного фактора резко замедляется, что можно трактовать как наиболее подходящие формы корреляционной зависимости, несмотря на то что у них, как это ни парадоксально с точки зрения теории математической статистики, наименьший R2.

Поэтому, на наш взгляд, наиболее подходящим является использование степенной или логарифмической зависимостей, выбор между которыми можно сделать, лишь решая какую-то конкретную задачу, а не проблему в целом.

Конкретные показатели того или иного уравнения полностью зависят от множества характеристик статистической выборки, которая необходима трейдеру: исходной базы информации, количества рассмотренных компаний, временных интервалов.

Однако независимо от того, в пользу какой зависимости делается выбор участником рынка, уже приведенный прогнозный пример показывает, что доля случайного фактора уменьшается вовсе не пропорционально росту временного интервала, а скорее по гиперболе, что позволяет говорить о том, что у тенденции к снижению случайного фактора обязательно имеется свой количественный предел.

Теоретически наличие (существование) такого предела вытекает из того, что никому и никогда не удастся избавиться от случайности изменения цены акции, как бы мы ни увеличивали временной интервал. Закономерность существует только в единстве со случайностью. «Обнуление» случайного фактора означало бы, что нечто стало только закономерным, что просто невозможно.

Таким образом, из проведенного исследования можно сделать два главных вывода:

• 1.    В цене акции всегда сосуществуют случайность и закономерность изменения. Невозможно избавиться от случайного характера изменения цены акции, но и не следует пренебрегать существованием закономерности этих изменений. Торговец на фондовом рынке, который основывается только на понимании случайного характера изменения цены акции, может упустить существенную выгоду от ситуации на рынке, для которой характерен процесс следования цены акции за существенным ростом капитала соответствующей компании. И наоборот, «слепое» следование возникшему на рынке, например, повышательному тренду, трактуемому трейдером как некая ценовая закономерность, может обернуться для него крупными потерями, поскольку сам этот тренд может быть результатом случайного одностороннего неравновесия спроса и предложения по данной акции, а вовсе не результатом роста капитала компании.

• 2.    С увеличением временного интервала доля случайного фактора в изменении цены акции имеет тенденцию к снижению, но только до определенного предела. Обычно считают, что инвестирование, т.е. покупка акции на длительные сроки, есть некая гарантия того, что ее цена обязательно существенно вырастет. На самом деле из единства закономерного и случайного в цене акции следует, что даже с течением времени от случайного момента в ее ценообразовании невозможно избавиться. Случайным обязательно будет, по крайней мере, тот момент, насколько вырастет цена данной акции. Ведь капитал компании возрастает благодаря не только усилиям, предпринимаемым самой компанией, но и наличию благоприятных условий для этого со сто-

• роны рынка соответствующего товара или услуги. Случайность, скрытая в самом товаре, заключается уже в том, что он «не вечен» и заменяем все новыми товарами. Отсюда, если цена акции будет расти в течение, например, срока инвестирования на пять лет, то это вовсе не гарантирует, что она будет расти и в случае инвестирования на срок десять лет. Закономерность изменения цены акции есть результат столкновения случайных многочисленных рыночных факторов, и даже небольшое измене-
• ние в их наборе и размерах снова приводит к хаотичности рыночной цены акции.

Именно поэтому профессиональные инвесторы на фондовом рынке обычно «инстинктивно» понимают, что нельзя инвестировать на длительные сроки. Само инвестирование имеет некие разумные сроки, за пределами которых это инвестирование превращается в свою противоположность – в спекулятивную игру на случайных изменениях цены акции с непредсказуемым результатом.