Случайное поведение участника как способ максимизации вероятности его выигрыша в парадоксе Монти Холла

В условиях дефицита ресурсов всех видов люди стремятся принимать рациональные решения (нормативный принцип поведения). Принятие решения основывается на анализе доступной информации и ее корректной интерпретации, однако человеческий мозг устроен таким образом, что делается это путем интуитивных оценок, а не точных расчетов [1]. Поскольку мерой качества возможного решения обычно является здравый смысл, противоречащие ему варианты часто отбрасываются как неэффективные. Если строгое научное обоснование рационального выбора противоречит здравому смыслу, возникает парадокс. Одним из таких парадоксов теории принятия решений является парадокс Монти Холла – задача, привлекшая наше внимание при просмотре фильма 2008 года «Двадцать одно» и имеющая почти полувековую историю. Наиболее ранняя ее постановка датируется, по-видимому, 1975 годом и представляет собой статью в американском журнале «American Statistical Association» [2]. В терминах естественного языка задача формулируется следующим образом. Представьте, что Вы – участник игры, в которой необходимо выбрать одну из трех дверей, за одной из которых находится автомобиль, а за двумя другими – козы. Вы выбираете одну из дверей, после чего ведущий (Монти Холл), который знает, где находится автомобиль, открывает одну из оставшихся дверей, за которой находится коза. После этого

Вам (участнику) предлагается решить: открыть выбранную ранее дверь или сменить свой выбор и открыть ранее не выбранную дверь. При этом предполагается, что вероятности нахождения автомобиля за каждой из дверей одинаковы; ведущему известна дверь, за которой находится автомобиль; ведущий обязан открыть дверь, за которой находится коза, отличную от той, которую выбрал участник, и предложить участнику изменить свой выбор; если ведущий может открыть две двери с козами, он выбирает любую из них произвольно, т. е. с равными вероятностями.

С точки зрения здравого смысла нет никакого смысла менять выбор на втором шаге, поскольку вероятность выигрыша составляет 1/2. Однако математически обоснованным оптимальным вариантом поведения участника является смена выбора, позволяющая повысить вероятность выигрыша с 1/3 при сохранении выбора до 2/3. Несмотря на то, что описанный парадокс не имеет непосредственного практического приложения (за исключением азартных игр, в частности, в бридже в форме принципа ограниченного выбора), задача вот уже в течение полувека активно обсуждается специалистами в области математики и психологии по причине полностью противоречащего интуиции решения и существенных трудностей в понимании решения людьми – по данным [3] от 79 до 87 % людей различных национальностей предпочитают сохранять свой изначальный выбор.

В классической постановке [4–8] задача считается вероятностной, а ее решение предполагает оценку вероятности выигрыша автомобиля при сохранении и смене выбора дверей. Кроме того, существуют решения задачи в терминах теории игр и доминирования стратегий [9], сетевых графических моделей [10], в рамках практического эксперимента [11, 12]. Исследователей-психологов интересуют причины затруднений, возникающие у большинства людей при принятии правильного решения в предложенной ситуации [13–16]. Отметим, что большинство исследований англоязычные, качественные отечественные публикации по теме, содержащие формальную математическую постановку и подробное убедительное решение задачи, по крайней мере в открытом доступе, нами не обнаружены. Кроме того, показавшаяся нам естественной постановка парадокса Монти Холла как задачи принятия решения в условиях неполной информации [17, 18], решением которой является обоснованный выбор оптимального поведения участника, в литературе также не найдена, что определяет актуальность и цель данного исследования.

1. Постановка задачи

Для формальной постановки задачи введем следующие обозначения:

– множество вариантов поведения участника на первом шаге

X 1 = { x 11 = (участник выбирает дверь № 1); x 12 = (участник выбирает дверь № 2);

x 13 = (участник выбирает дверь № 3)};

– множество вариантов поведения ведущего на втором шаге

Y 1 = { y 21 = (ведущий открывает дверь № 1); y 12 = (ведущий открывает дверь № 2);

y 13 = (ведущий открывает дверь № 3)};

– множество вариантов поведения участника на третьем шаге

X 3 = { x 31 = (участник не меняет свой выбор и открывает дверь, выбранную на первом шаге);

x ₃₂ = (участник изменяет свой выбор и открывает дверь, отличную от выбранной на первом шаге)}.

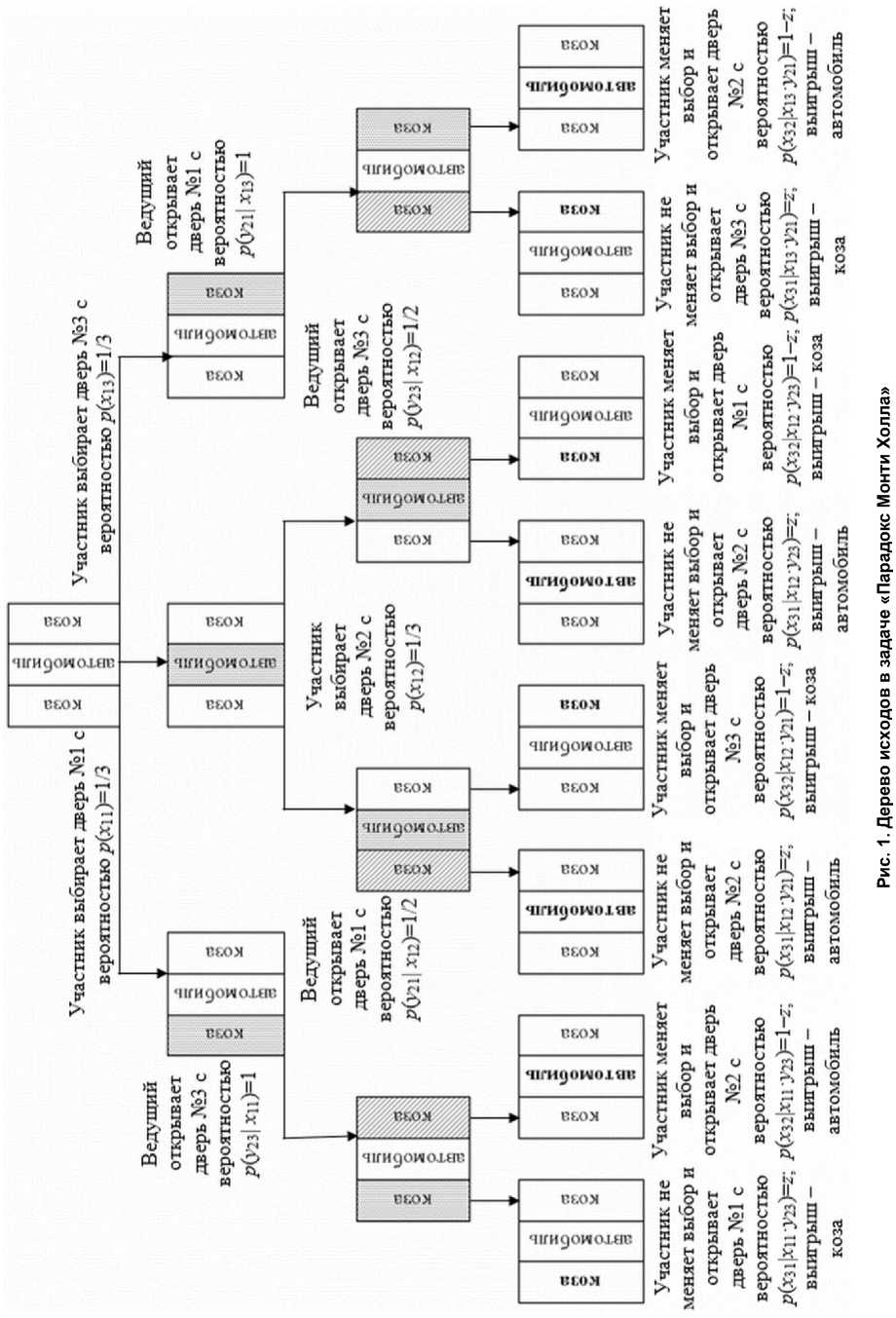
Рациональная последовательность имеющихся в распоряжении участника и ведущего вариантов поведения в предположении, что автомобиль находится за второй дверью, позволяет сформировать дерево исходов задачи (рис. 1).

Если автомобиль находится за первой (третьей) дверью, то в дереве меняются местами второе и первое (третье) поддеревья, начиная с корневой вершины, т. е. расположение выигрышной двери меняет не структуру дерева, а его форму, и не влияет на результат решения. Кроме того, очевидно, что поддеревья для случаев, когда участник выбирает любую из дверей с козой, имеют одинаковую структуру.

• 2.    Решение задачи «Парадокс Монти Холла» путем максимизации вероятности выигрыша участника по вероятности сохранения им выбора на третьем шаге Поскольку по условию задачи вероятности нахождения автомобиля за каждой из дверей одинаковы, то и выбор двери участником на первом шаге также равновероятен, т. е. p ( x 11 ) = p ( x 12 ) = p ( x 13 ) = 1/3. Если участник на первом шаге выбрал первую (третью) дверь с козой, то ведущий может открыть лишь третью (первую) дверь, поскольку он должен открыть дверь, за которой находится коза, отличную от той, что выбрал участник, т. е. p ( y 23 | x 11 ) = p ( y 21 | x 13 ) = 1. Если же участник на первом шаге выбрал дверь, за которой находится автомобиль, то ведущий с равными вероятностями может открыть любую из дверей (первую или третью), за которыми находятся козы, т. е. p ( y 21 | x 12 ) = p ( y 23 | x 12 ) = 1/2. Предположим, что на последнем шаге участник реализует смешанную стратегию, и обозначим вероятность сохранения участником своего выбора на третьем шаге p ( x 31 ) = z , следовательно, вероятность смены участником своего выбора на третьем шаге как вероятность противоположного x 31 события равна p ( x 32 ) = 1 – z . Тогда:

• – если участник на первом шаге выбрал первую (третью) дверь, то при сохранении своего выбора с вероятностью p ( x 31 | x 11 · y 23 ) = p ( x 31 | x 13 · y 21 ) = z он получает козу, а при смене выбора с вероятностью p ( x 32 | x 11 · y 23 ) = p ( x 32 | x 13 · y 21 ) = 1 – z – автомобиль;

  – если участник на первом шаге выбрал вторую дверь, то при сохранении своего выбора и любой открытой на втором шаге двери он выигрывает автомобиль с вероятностью p ( x 31 | x 12 · y 23 ) = p ( x 31 | x 12 · y 21 ) = z , а при смене выбора с вероятностью p ( x 32 | x 12 · y 23 ) = p ( x 32 | x 12 · y 21 ) = 1 – z – козу.

• 3.    Экспериментальное решение задачи «Парадокс Монти Холла»

Оптимальным будем считать тот вариант поведения на третьем шаге, который обеспечивает максимум вероятности выигрыша автомобиля. Анализ дерева исходов позволил установить, что вероятность выиграть автомобиль при условии сохранения участником своего выбора на третьем шаге составляет P_W | x ₃₁( z ) = z /3, а вероятность выиграть автомобиль при условии изменения участником своего выбора на третьем шаге составляет P W | x 32 ( z ) = 2∙(1– z )/3. Тогда по формуле полной вероятности совокупная вероятность выигрыша составит P W ( z ) = p ( x 31 )· P W | x 31 ( z ) + p ( x 32 )∙ P W | x 32 ( z ) = = z ∙ z /3 + (1 – z )∙2∙(1 – z )/3 = z ² – 4∙ z /3 + 2/3 = ( z – 2/3)² + 2/9. Поскольку z – вероятность, т. е. z ∈ [0; 1], то задача максимизации вероятности выигрыша представляет собой задачу нахождения максимального значения функции P W ( z ) на отрезке z ∈ [0; 1]. Функция P W ( z ) представляет собой параболу с ветвями, направленными вверх, и минимумом в точке z = 2/3. Это означает, что максимума функция достигает на одном из концов рассматриваемого отрезка. Поскольку P W ( z = 0) = = 0² – 4∙0/3 + 2/3 = 2/3, а P W ( z = 1) = 1²–4∙1/3 + 2/3 = 1/3, то максимальное значение вероятности выигрыша составляет P_W ^max ( z ) = 2/3 и достигается при нулевой вероятности сохранения участником своего выбора на третьем шаге p ^*( x 31 ) = z ^* = 0. Тогда вероятность смены участником своего выбора на третьем шаге, обеспечивающая максимум вероятности выигрыша, равна p ^*( x 32 ) = 1 – z ^* = = 1 – 0 = 1. Это означает, что наиболее рациональная стратегия поведения участника – x 32 = (участник изменяет свой выбор и открывает дверь, отличную от выбранной на первом шаге).

Полученный результат, вообще говоря, противоречит здравому смыслу, подсказывающему, что на последнем шаге вероятности выиграть и проиграть одинаковы и равны 1/2, поскольку выбирать приходится из двух дверей, за каждой из которых с одинаковой вероятностью находится автомобиль. Чтобы проверить правильность полученного решения задачи, мы провели численный эксперимент, в котором подсчитали относительную частоту выигрышей и проигрышей участника при различных значениях p ( x ₃₁) = z . Эксперимент был реализован в соответствии со следующим алгоритмом:

• 1)    генерируется первое случайное число A , равное 0, 1 или 2, как остаток от деления случайного целого положительного числа на 3, тогда A + 1 – номер двери, за которой находится автомобиль;

• 2)    аналогично генерируется второе случайное число B , равное 0, 1 или 2, тогда B + 1 – номер двери, выбранной участником на первом шаге;

• 3)    генерируется третье случайное число C , равномерно распределенное на отрезке [0; 1], если его величина меньше заданного p ( x 31 ) = z , то считаем, что участник не меняет свой выбор на

третьем шаге, если же С превышает p ( x 31 ) = z , то считаем, что участник меняет свой выбор на третьем шаге;

• 4)    если участник на первом шаге выбрал дверь, за которой находится автомобиль (т. е. A = B ), то при C <  z (сохранение выбора) он его выигрывает, если же участник выбрал на первом шаге дверь с козой ( A ≠ B ), то автомобиль он выиграет при C >  z (смена выбора).

Алгоритм реализован средствами пакета Mathcad, нами были определены относительные частоты выигрышей участником автомобиля при различных значениях вероятности сохранения им своего выбора, начиная от нуля и заканчивая единицей с шагом h = 0,1 и числом итераций N = 100 000. Для получения наиболее полного описания ситуации были подсчитаны относительные частоты выигрышей участника при сохранении и смене им выбора двери на третьем шаге ( P ^ˆ W | x 31 ( z ) и P ^ˆ W | x 32 ( z ) соответственно), а также определена совокупная относительная частота его выигрыша P ^ˆ W ( z ) = z · P ^ˆ W | x 31 ( z ) + (1 – z )∙ P ^ˆ W | x 32 ( z ) (рис. 2). Очевидно, что 1/3 = z /3 = P W | x 31 ( z = 1) ≈ ≈ P ^ˆ W | x 31 ( z = 1) = 0,33 и 2/3 = 2∙(1 – 0)/3 = P W | x 32 ( z = 0) ≈ P ^ˆ W | x 32 ( z = 0) = 0,67, т. е. точные вероятности выигрышей приблизительно равны соответствующим относительным частотам. Кроме того, максимум совокупной относительной частоты выигрыша, равный P ^ˆ _W ^max ( z ) = P ^ˆ W | x 32 ( z ) = 0,67, действительно достигается при z = 0, т. е. при смене участником двери на третьем шаге. Таким образом, численный эксперимент полностью подтверждает правильность аналитического решения задачи.

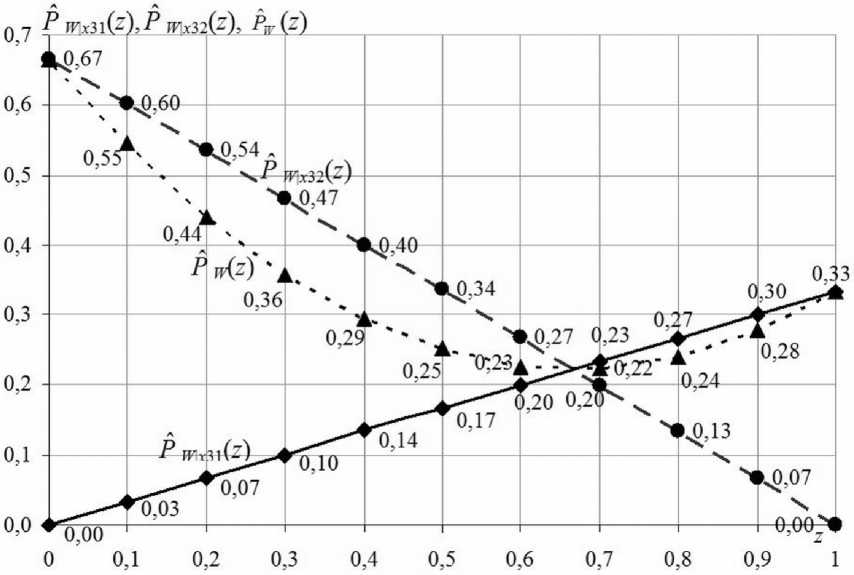
Рис. 2. Относительные частоты выигрыша автомобиля при различных вероятностях сохранения участником выбора на третьем шаге

Заключение

В рамках проведенного нами исследования выполнена формальная математическая постановка парадокса Монти Холла как задачи принятия решения. Задача решена двумя способами – аналитически и экспериментально. Аналитически оптимальный вариант поведения участника определен исходя из максимума вероятности выигрыша автомобиля. Экспериментальное решение найдено путем подсчета относительных частот выигрышей при многократной компьютерной имитации ситуации. Оба варианта решения привели к одинаковым результатам: наиболее рациональным вариантом поведения участника является реализация чистой стратегии x32 = (участник изменяет свой выбор и открывает дверь, отличную от выбранной на первом шаге). Вероятность выигрыша автомобиля в этом случае максимальна и равна 2/3, тогда как при сохранении выбора двери вероятность выигрыша вдвое меньше и составляет 1/3. Реализация смешанной стратегии, заключающейся в том, что вариант x31 выбирается с вероятностью z > 0, а x32 – с вероятностью 1 – z < 1 приводит к снижению вероятности выигрыша PW(z) = (z – 2/3)2 + 2/9, а значит, нерациональна.