Снижение усилий приводов при обработке на станках с параллельной кинематикой

Современное технологическое оборудование в большинстве случаев строится с использованием кинематических схем, предполагающих последовательное расположение механизмов, обеспечивающих взаимное перемещение рабочего органа (инструмента) и заготовки. Типичным представителем подобного оборудования является 3-координатный фрезерный станок, показанный на рис. 1. Как видно из рисунка, по координате X соответствующий привод помимо инструмента (фрезы) должен перемещать элементы станка, обеспечивающие перемещение инструмента по координатам Y и Z. Аналогично привод координаты Y должен перемещать элементы станка, обеспечивающие перемещение инструмента по координате Z. Очевидно, что такое построение требует увеличения массы подвижных частей станка и мощности приводов.

При обработке на 3-координатных фрезерных станках широко используется плоское фрезерование, при котором осуществляется перемещение инструмента по координатам X и Y при фиксированной координате Z . В этом случае движения по координатам X и Y являются основными формообразующими движениями. В работе [1] показано, что за счет рационального расположения заготовки на столе станка можно обеспечить снижение потребляемой приводами координат X и Y энергии. Покажем, что положение заготовки влияет также и на усилия, развиваемые приводами.

Рассмотрим процесс выполнения операции плоского фрезерования, при котором обеспечивается перемещение продольной оси фрезы вдоль направления, задаваемого вектором dL (рис. 2, а). При фрезеровании на фрезу будет действовать сила P - сила резания, которая может быть представлена следующими составляющими: Р _т - тангенциальной, параллельной dL , и P n -нормальной, перпендикулярной dL .

Z

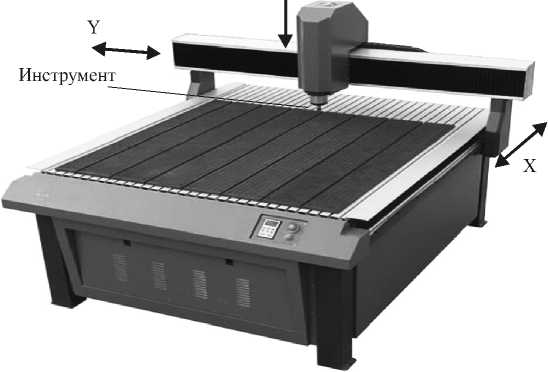
Рис. 1. Схема 3-координатного фрезерного станка

Свяжем с неподвижным столом, на котором закреплена заготовка, систему координат (СК) OXY . При фрезеровании заготовка может иметь различные угловые положения (рис. 2), следовательно, для удаления одного и того же материала при различных угловых положениях заготовки потребуется обеспечить движение инструмента в СК OXY по различным траекториям. Примем, что угловое положение заготовки и направление вектора dL задается углом ф , откладываемым от оси OX .

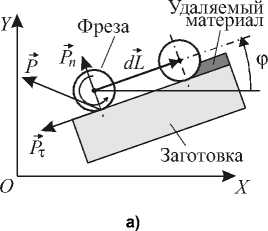
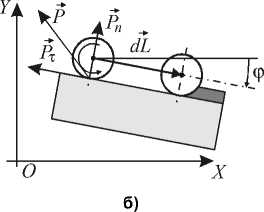
Рис. 2. Элементарное перемещение фрезы

При перемещении фрезы каждый из приводов преодолевает усилия, определяемые составляющими P _т и P n силы резания (силы трения и динамические нагрузки не учитываются):

P X = P _T cos ф+ P n sin ф , P Y = P _T sin ф- P n cos ф .

На рис. 3 показаны результаты расчетов модулей усилий P X и P Y при различных направлениях движения фрезы, определяемых углом ф . Принято, что P _T = 100 Н, P n = 10 Н. Как видно из графика, за счет изменения углового положения заготовки можно изменять величины усилий, развиваемых приводами.

Следовательно, может ставиться и решаться задача оптимального размещения (ориентации по углу ф ) заготовки на столе фрезерного станка с целью перераспределения усилий, необходимых для выполнения операции фрезерования, между приводами станка. Цель перераспределения – снижение усилия, развиваемого максимально нагруженным приводом:

P max = max(| ^PX ( ф )|, P Y ( ф )^ ^ min.                                                      (1)

В рассматриваемом случае плоского фрезерование с использованием двух приводов выполнение условия (1) приведет к равенству | P X | = | P_Y | (рис. 3).

Решение задачи (1) позволит:

– при заданных режимах обработки снижать нагрузку на элементы конструкции станка и приводы, тем самым увеличивая их ресурс;

Тверской М.М., Смирнов В.А., Сюськина Ю.Л.

– при заданных ограничениях на усилия, развиваемые приводами, реализовывать режимы обработки с большими подачами, тем самым снижая время обработки и повышая производительность оборудования.

Задача относительно просто решается и реализуется на практике для линейной траектории движения фрезы и при постоянстве величин Р _т и P n . В этом случае заготовка может быть закреплена рациональным образом на столе станка перед началом фрезерования; в процессе фрезерования изменение положения заготовки для обеспечения условия (1) не потребуется.

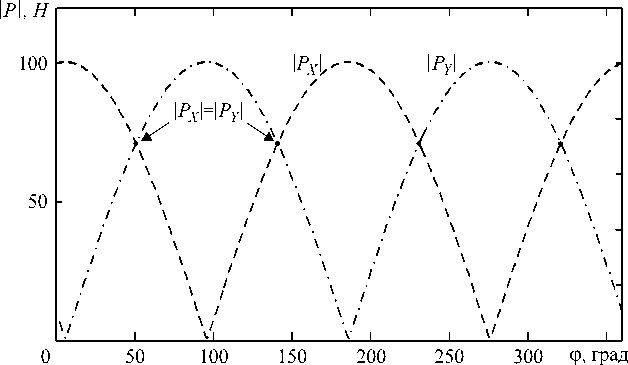
Рис. 3. Зависимость усилий, развиваемых приводами, от углового положения заготовки

В случае реализации кусочно-линейных и криволинейных траекторий движения фрезы или при непостоянстве составляющих силы резания для обеспечения рационального расположения заготовки потребуется дополнить станок приводом, обеспечивающим поворот заготовки относительно оси Z . Это существенно усложнит конструкцию станка.

Задача снижения усилий, развиваемых приводами станка в процессе фрезерования, может более просто решаться применительно к станкам с параллельной кинематикой, которые строятся на основе механизмов с параллельными кинематическими цепями (МПКЦ). При этом может использоваться понятие «избыточная координата» [2, 3].

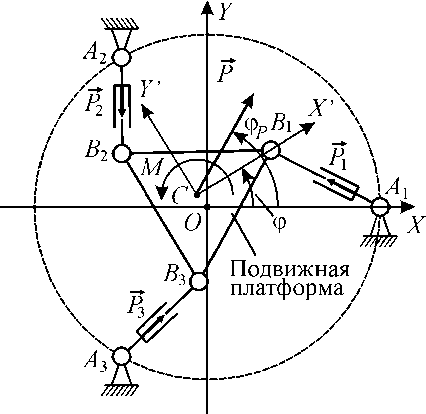
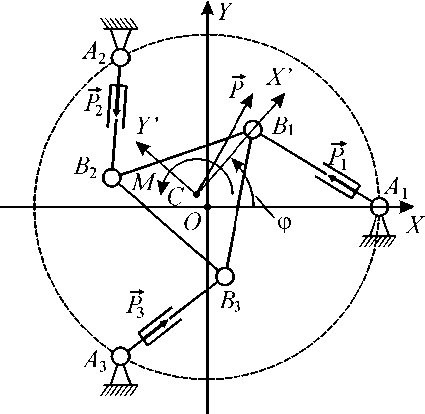
Рассмотрим плоский МПКЦ, показанный на рис. 4, а. Механизм имеет три степени свободы: за счет изменения длин A j B j штанг полюс С подвижной платформы может перемещаться по двум линейным координатам Хи Y , платформа может поворачиваться вокруг полюса на угол ф . На платформе устанавливается шпиндель с фрезой; продольная ось фрезы проходит через полюс платформы. Механизм позволяет осуществлять формообразующие движения по линейным координатам; возможность поворота платформы позволяет выполнять перераспределения усилий приводов штанг при заданных условиях обработки.

Действительно, если не рассматривать влияние сил трения и инерционных нагрузок, возникающих при движении элементов реального оборудования, то усилия P j , развиваемые приводами, связаны с составляющими силы резания следующими уравнениями:

• ' a_n P i + a i2 P 2 + a_n Р 3 = - Р cos ф p ;

• ‘ a 21 P i ⁺ a 22 p ⁺ a 23 P = ^- P sin ф p ; (2)

a 31P + a32 P2 + азз P3 = — M, где коэффициенты ау зависят от координат шарниров Aj и Bj; угол фР определяет направление силы резания в неподвижной СК OXYZ, связанной с основанием; момент M = РтRФр, RФр - радиус фрезы. В СК OXYZ координаты шарниров Aj будут постоянны. Координаты шарниров Bj будут определяться текущими значениями координат xC и yC полюса платформы и ее углом поворота ф, т. е. выходными координатами рассматриваемого механизма. Следовательно, при постоянстве правых частей уравнений (2) и выходных координат xC и yC (см. рис. 4, а и б) изменение выходной координаты ф приведет к изменению усилий Pj.

а)

б)

Рис. 4. Плоский МПКЦ с 3 степенями свободы

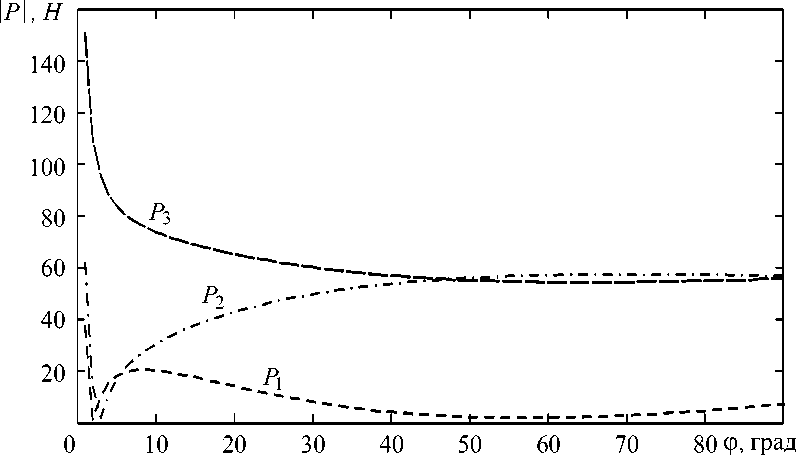
Рис. 5. Зависимость усилий приводов, необходимых для компенсации заданного воздействия, от угла разворота подвижной платформы

На рис. 5 показаны результаты моделирования изменения величин уси л ий P j для р ассматриваемого МПКЦ при изменении угла ф . При моделировании было принято, что шарниры A j равномерно расположены на окружности радиусом 200 мм; шарниры B j – на окружности радиусом 100 мм; начало неподвижной СК совпадает с центром окружности, на которой расположены шарниры A j ; x_C = -10 мм, y_C = 10 мм, Р _т = 100 Н, P n = 10 Н ( Р ~ 100,5 Н), ф _Р = 60 ° , R _Фр = 5 мм.

Для рассматриваемого механизма выражение, а н алогичное (1), будет и м еть следующий вид:

P max = ^max(| ^P 1M , I P Wl, | ^Р 3 ⁽ ф )|) ^ min ^{.                                                (3)}

Выполнение условия (3) на рис. 5 происходит п р и ф = 47 ° .

Таким образом, за счет рационального изменения выходной «избыточной» координаты ф можно обеспечить снижение усилий приводов, необходимых для выполнения конкретной технологической операции.

На рис. 6 показаны результаты моделирования м аксимального из уси л ий P j при фрезеровании отверстия круглой формы с использованием МПКЦ, геометрические размеры которого приведены выше. Принято, что выходная угловая координата ф может изменяться в диапазоне от 10 до 60 градусов. Положение полюса при его движении по окружности опр е деляется у г ловой координатой ф . График 1 соответствует случаю постоянства координаты ф = 10 ° . График 2 соответствует управлению, обеспечивающему выполне н ие условия (3). Моделирование показало снижение максимального из усилий на 50,1 %.

Снижение максимального усилия достигается за счет изменения координаты ф по показанному на рис. 7 закону. Анализ графика показывает, что значение угла ф для заданных при моде- лировании условиях близко или совпадает с максимально допустимым значением в 60 градусов. Если принять, что угол ф = 55° и в процессе фрезерования остается неизменным, то значения максимального из усилий приводов будут практически совпадать с минимизированными в соответствии с (3) (см. график 3 на рис. 6).

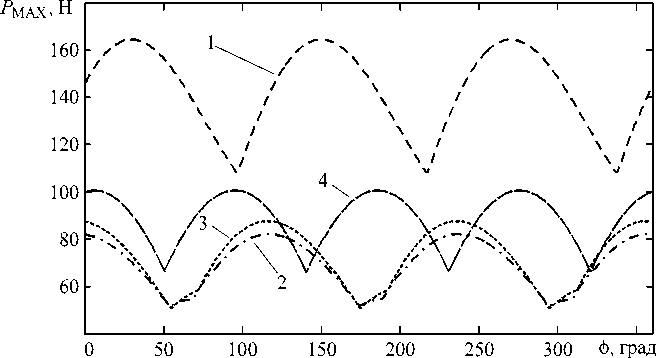
Рис. 6. Моделирование максимального из усилий приводов при фрезеровании отверстия круглой формы ф, град

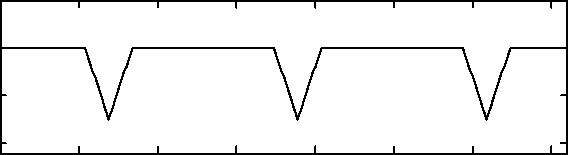
0      50      100 150 200 250 300 Ф , град

Рис. 7. Изменение угла ф, обеспечившее снижение максимального из усилий приводов при фрезеровании отверстия круглой формы

График 4 на рис. 6 отражает результаты моделирования максимального из усилий приводов фрезерного станка с последовательной схемой (см. рис. 1) при фрезеровании на нем отверстия круглой формы. Принято, как и ранее, Р _т = 100 Н, P n = 10 Н. Сравнение графиков 2, 3 и 4 показывает, что для выполнения одной и той же технологической операции в станке с параллельной кинематикой потребуются приводы, способные развивать меньшие усилия.

Реализация в оборудовании с параллельной кинематикой оптимального управления, при котором за счет рационального выбора выходной координаты ф обеспечивается условие (3), может быть осуществлена двумя способами:

• 1.    Анализ внешних воздействий (определение силы резания) осуществляется на этапе моделирования предполагаемых технологических операций; в результате формируется закон изменения координаты ф , обеспечивающий выполнение требуемой технологической операции с учетом условия (3).

• 2.    При работе оборудования производится измерение усилий, развиваемых приводами, на основе чего вносятся изменения в текущие значения выходной координаты ф с целью выполнения условия (3).

Второй способ обладает большей универсальностью, так как он, в отличие от первого, не привязан к конкретным условиям (подача, снимаемый припуск и т. п.). Получение информации о развиваемых приводами усилиях сложности не представляет: например, широко используемые при построении технологического оборудования следящие приводы имеют в своем составе контур регулирования по создаваемому усилию (моменту) [4], что предполагает измерение этих величин.

Заключение. Рассмотренный подход к управлению станками с параллельной кинематикой позволяет снизить усилия, развиваемые приводами при реализации операции фрезерования. Это позволит:

• –    при заданных режимах обработки снижать нагрузку на элементы конструкции станка и приводы, тем самым увеличивая их ресурс;

• –    при заданных ограничениях на усилия, развиваемые приводами, реализовывать режимы обработки с большими подачами, тем самым снижая время обработки и повышая производительность оборудования.

Результаты моделирования показали возможность снижения максимального из усилий приводов более чем на 50 %.