Собственные колебания усечённых конических оболочек переменной толщины
Автор: Бочкарв Сергей Аркадьевич
Журнал: Вычислительная механика сплошных сред @journal-icmm
Статья в выпуске: 4 т.13, 2020 года.
Бесплатный доступ
Представлены результаты исследований собственных частот колебаний круговых усечённых конических оболочек, толщина стенок которых непостоянна по длине и изменяется по различным законам. Поведение упругой конструкции описывается в рамках классической теории оболочек, основанной на гипотезах Кирхгофа-Лява. Соответствующие геометрические и физические соотношения совместно с уравнениями движения сводятся к системе обыкновенных дифференциальных уравнений относительно новых неизвестных. Решение сформулированной краевой задачи осуществляется методом ортогональной прогонки Годунова с численным интегрированием дифференциальных уравнений методом Рунге-Кутты четвёртого порядка точности. Для вычисления собственных частот колебаний используется сочетание пошаговой процедуры с последующим уточнением методом деления пополам. Достоверность полученных результатов подтверждена сравнением с известными численно-аналитическими решениями. Для оболочек с различными граничными условиями (свободным опиранием, жёстким и консольным закреплением), углами конусности и линейными размерами найдены зависимости минимальных частот колебаний при степенном (линейном и квадратичном, имеющих симметричную и несимметричную формы) и гармоническом (с положительной и отрицательной кривизной) изменении толщины стенки. Продемонстрировано существование конфигураций стенок, обеспечивающих значительный рост частотного спектра по сравнению с оболочками постоянной толщины при одинаковых ограничениях на вес конструкций.
Классическая теория оболочек, коническая оболочка, метод ортогональной прогонки годунова, собственные колебания, переменная толщина
Короткий адрес: https://sciup.org/143172505
IDR: 143172505 | УДК: 534-13 | DOI: 10.7242/1999-6691/2020.13.4.31
Текст научной статьи Собственные колебания усечённых конических оболочек переменной толщины
Известно [1], что в прикладных задачах максимизация минимальной (фундаментальной) моды колебаний требуется для расширения безрезонансного диапазона частот конструкции с целью повышения её эксплуатационных характеристик. Для оболочек вращения, как структурных элементов в многообразных технических приложениях, повышение нижней частоты колебаний наряду с выбором подходящих граничных условий, геометрических размеров, переменной жёсткости, начальных напряжений, углов армирования и другого [2–6] может быть также достигнуто посредством задания неравномерной толщины стенок [7]. В случае усечённых конических оболочек, являющихся объектом исследования в настоящей работе, оценка влияния на частотный спектр толщины, тем или иным образом меняющейся по длине, осуществлялась также в [8–26]. В этих работах представлены результаты изучения влияния различных параметров на свободные колебания изотропных, ортотропных, композитных, слоистых и подкреплённых оболочек, толщина стенок которых изменяется по степенному, экспоненциальному или гармоническому законам, на основе численных и численно-аналитических методов (коллокаций, вейвлет-анализа, Рэлея–Ритца, разложения в степенные ряды, конечных элементов, дискретного ортонормирования). Но среди перечисленных публикаций лишь в [17–19, 21] внимание акцентируется на максимизации нижней частоты колебаний относительно референсной, за которую принимается частота оболочки с постоянной толщиной и эквивалентной массой. К тому же исследования ограничиваются только случаем изменения толщины по линейному закону. Аналогичное обсуждение оболочек цилиндрической формы в [27, 28] осуществлено для большего количества вариантов изменения толщины. При этом отмечается, что варьирование толщины стенки согласно квадратичному закону значительнее всего влияет на рост фундаментальной частоты. Выполнение подобного анализа для конических оболочек, предполагающего вовлечение более разнообразных законов изменения толщины по длине, чем это представлено в литературе, является целью настоящей работы.
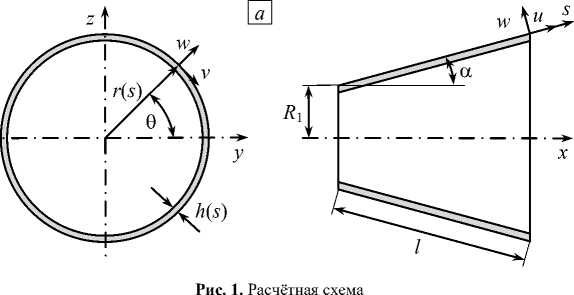
Рассматривается усечённая коническая оболочка (Рис. 1) с минимальным радиусом R , углом при вершине а и образующей длиной l . Толщина стенки оболочки h = h ( s ) переменна по длине образующей и математически описывается как h = hg ( s ). Здесь h — эквивалентная толщина, вычисляемая относительно референсной толщины h , и g ( s ) — функция меридиональной координаты s , определяющая закон изменения толщины.

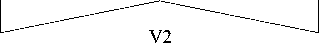
V1
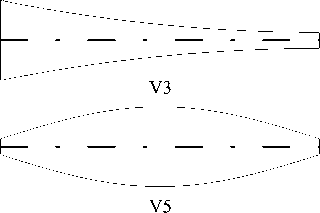
Рис. 2. Продольное сечение стенок оболочки c различными вариантами изменения толщины: V1 – линейный несимметричный; V2 – линейный симметричный; V3 – квадратичный несимметричный; V4 – квадратичный симметричный; V5 – гармонический выпуклый; V6 – гармонический вогнутый
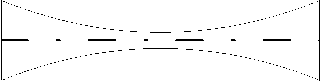
V4
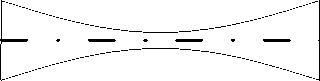
V6
На рисунке 2 представлены варианты толщин стенок оболочки, которым отвечает функция g ( s ) вида:
-
V 1: g ( s ) = 1 + k |H ;
-
V 3: g ( s ) = 1 + k 0;- 1 ) 2 ;
-
V 5: g ( s ) = 1 + k sin (лУ ;
V2: g ( s ) = 1 + k |2H;
V4: g ( s ) = 1 + k ( 2 ^- 1 ) 2 ;
V6: g ( s ) = 1 + k [ 1 - sin ( л^ ) ]
где ^ = s/l , k — коэффициент, характеризующий переменность толщины. Величина he вычисляется из условия эквивалентности масс с референсной оболочкой по следующим формулам:
V1, V2:
h = ^h o.. e ;
2 + k
V5:
h = ;
e 2k+ n’
V3, V4:
h = ;
e 3 + к
V6:
п ho
—-------------- .
пк + п — 2 к
Как видно из формул, при к — 0 толщина оболочки постоянна и равна h — h0 .
Итак, ставится задача исследования влияния толщины, описываемой разными законами, на частотный спектр усечённой конической оболочки как при её различных линейных размерах, так и при кинематических граничных условиях, задаваемых на краях исходя из условия эквивалентности масс для конкретного угла конусности.
3. Основные соотношения
Для классической теории оболочек, основанной на гипотезах Кирхгофа–Лява, компоненты вектора деформации Eiy в криволинейной системе координат { s , 0 , z} могут быть представлены в виде [29]:
Е„ — е„ + z к ,, ,
Е е 22
— е22 + z к22,
Е 12 S 12 + 2 z К 12 ,
|
где |
sn — и ' + rw , S22 — V "+v и + rw , s12 — V ' + и •— v V , кп — 0‘ , к22—0^+v0i , к12—0^—v02+ rV ', 0i—— w ' + ru , 02 — — w " + rv , (1) z v 1 d( - ) z v 1 5( ^ ) 1 ( _ ) — , ( _ ) — , v — A 2 . A d s A d0 A 2 |
Здесь: A , A — коэффициенты Ламе; r , r — кривизны; u , v, w — меридиональная, окружная и нормальная составляющие вектора перемещений оболочки; 0,, 02 — углы поворота недеформируемой нормали.
Физические соотношения, устанавливающие связь между вектором усилий и моментов T — { T ,т T 2, S , Mxр M, 2, H } т и вектором обобщённых деформаций s — {Sj р s2 2, Sj 2, к р к22,2к12 } т, в матричном виде записываются как
Здесь величины, составляющие матрицу жёсткостей D, являются функциями меридиональной координаты s и вычисляются по формулам:
ay(s) — J Qydz, by(s) — J zQydz, cy(s) — J z2Qydz (i, y —1,2,3) , (3)
h ( s ) h ( s ) h ( s )
где коэффициенты Qy определяются известным образом [29] относительно модулей упругости ( E р Е 22), коэффициента Пуассона (V,2) и модуля сдвига ( G 12) материала оболочки.
Уравнения движения оболочки имеют вид:
d 2 и
T 11 + v( T 11 — T 22 ) + S + r l ( Q 11 — H ) —Р о“ГГ — 0 d t
S 2 + 2 у ( S + г H ) + T ^ + r 2 ( Q 22 + H ') — Р о -У — 0, d t
Q‘ 1 + v Q 11 + Q 2 ^ 2 — r 1 T 1
—
d2w r2T22 p0 д 2 0
d t
M‘ + v( M11 — M 22) + H •— Q11 — 0, H' + 2v H + M ;2— Qn — 0,
где Q — поперечные силы, p0 ( s ) — [ p dz , p — плотность материала. ^0 J h ( s )--
Раскладывая в ряды Фурье по окружной координате 9 все параметры, описывающие поведение усечённой конической оболочки,
X(5,9) = Е Xj (5)cos (j9), Y(5,9) = Е Yj (5) sin (j9), j=0 j=0
X = { u, w, 91, Eu, E 22, K11, K 22, Tu, T22, M11, M 22, Qo}, Y = { v, 92, En, K12,5, H, Q22}, сведём геометрические (1) и физические (2) соотношения, а также уравнения движения (4) к системе восьми обыкновенных дифференциальных уравнений первого порядка относительно новых неизвестных [29]:
У 1 = T 1 , y 2 = 5 + 2 r H , y 3 = M 11 , y 4 = Q 11 + jH ,
У5 = u, У 6 = v, У 7 = w, У8 =
Здесь j = j/A2 , где j — номер гармоники при разложении в ряд Фурье. Принимая это во внимание и разыскивая решение в виде y ( t ) = y exp ( i ro t ) , запишем искомую систему следующим образом:
У’= f (j, ®, У), где f = j ( 2 r2 H - У 2 )—V(У1 - T22 )-r1 У4 -Ю2Ро У 5, f2 = jT22 - 2VУ 2 - r2 Q22 — ^0 У6, f3 = У4 — V( У3 -M 22 )-2 jH, f( = r1 У1 — VУ4 + r2 T22 - j ( Q22 + 2VH )-ГО2Ро У 7, f5 = E11 -r1 У 7, f, =E12 + VУ6 + jy5, f7 =- У8 + r1 У5, f; = Кш ro — частота колебаний, i2 = — 1. Входящие в выражения (6) величины с учётом (1), (2) вычисляются по формулам:
£ 22 = jy 6 + Г 2 У 7 + V У 5 , К 22 = j 9 2 + V У 8 , 9 2 = Г 2 У 6 + jy 7 , H = b 33 £ 12 + 2 c 33 К 12 ,
Q 22 = — jM 22 , К 11 = |^ a-ц ( y 3 — b 12 £ 22 — С 12 К 22 ) — Ь 11 ( У 1 — a 12 £ 22 — Ь 12 К 22 ) ]/( a 11 c 11 — Ь 11 ) ,
£ 11 = ( У 1 — a 12 £ 22 — b 11 K 11 — b 12 К 22 ) К1 , К 12 = r 2 ( Е 12 + jy 5 ) — 7 ( У 8 +V У 7 ) ,
T 22 = a 12 £ 11 + a 22 ^ 22 + Ь 12 К 11 + b 22 К 22 , M 22 = b 12 £ 11 + b 22 £ 22 + С 12 К 11 + c 22 К 22 ,
£ 12 = [ У 2 — 2 ( Ь .3 + 2 r 2 c 33 ) j ( Г 2 У 5 — У 8 — V У 7 ) ]/[ a 33 + 4 r 2 ( b 33 + r 2 c S3 ) ] .
На краях оболочки зададим однородные граничные условия:
y , L = 0 M У + 41 5 = 0 ( 1 —8 - ) = 0 (< = 1, - , 4 ) , (7)
У , Ь = l 8 , + 4 + У. + 4| 5 = L ( 1 — 5 , + 4 ) = 0 ( - = 1, ^ ,4 ) , (8)
где при известных кинематических и статических граничных условиях §г- = 0 и 5г- = 1 соответственно.
Систему (5) с граничными условиями (7), (8) будем решать далее методом ортогональной прогонки Годунова [30] с численным интегрированием дифференциальных уравнений методом Рунге–Кутты четвёртого порядка точности. Для этих целей её общее решение представим в виде:
у = Е C j^j , j = 1
где C — некоторые константы, а y — совокупность линейно независимых решений, удовлетворяющих граничным условиям (7). В результате интегрирования по заданному интервалу и удовлетворения граничных условий (8) для определения постоянных C получим следующую алгебраическую систему:
£ C j f j = 0 ( i = 1, _ ,4 ) .
j = 1
Таким образом, задача сводится к вычислению значений ю , при которых существует нетривиальное решение системы (9), при этом необходимым условием является равенство нулю определителя матрицы |f ( ю)| = 0. С этой целью воспользуемся комбинацией шагового метода и метода деления отрезка пополам. Посредством первого вычисляются такие значения ю , при которых происходит смена знака определителя f ( ю )|, а с помощью второго уточняются ю в полученном диапазоне их значений.
4. Численные результаты
В приведённых численных примерах рассматривается коническая оболочка ( Rx = 0,1, v = 0,3 ), которая по краям или свободно опёрта ( v = w = Tt = Mxx = 0, условное обозначение SS), или жёстко защемлена ( u = v = w = 0j = 0, CC), или имеет консольное закрепление ( T j = 0, 5 + 2 rH = 0, Mn = 0, Qu + jH = 0 ,
CF). Для представления результатов используются безразмерная частота Х = юl^р(1 -V2)^ExjJ или отношение частот ю/ю0 , где ю0 соответствует минимальной частоте колебаний оболочки постоянной толщины при аналогичном угле конусности. Переменность толщины задаётся с помощью параметра В = к -1 = hi / h -„ , где й „ и h . — максимальная и минимальная толщины профиля стенки. Примеры max min max min профилей оболочек с массой, эквивалентной референсной, при различных значениях параметра в и разных законах изменения толщины приведены на рисунке 3.
а

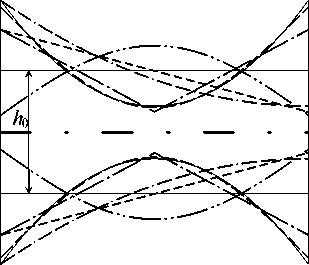
Рис. 3. Продольные сечения стенок оболочек c разными вариантами изменения толщины и эквивалентными массами при значениях параметра р : 2 ( а ); 5 ( б )
Для верификации описанного выше алгоритма осуществлено сравнение результатов, полученных на его основе, с известными из [31-33] данными для конической оболочки постоянной толщины при а = 45 ° , v12 = 0,3, h/R = 0,01. В таблице 1 для оболочек с различными граничными условиями приведены значения безразмерных минимальных частот X , соответствующих первым девяти окружным модам колебаний j . В случае оболочек переменной толщины выполнено сравнение с решением из работы [18], которое найдено методом конечных элементов. Минимальные частоты колебаний ю (Гц) и соответствующие им номера гармоник j , вычисленные в этой работе для жёстко закреплённой (CC) конической оболочки при Ехх = 181 ГПа, Е22 = 10,5 ГПа, G^ = 7,17 ГПа, v12 = 0,28, р = 1600 кг/м3, h/R = 0,01, R = 0,1 м и толщине, изменяющейся согласно линейному закону в симметричной конфигурации (вариант V2), представлены в таблице 2 для различных углов конусности а , линейных размеров R/l и разных значений параметра переменности толщины в . Из данных таблиц 1 и 2 следует, что полученные результаты хорошо согласуются с ранее опубликованными результатами численноаналитических и численных решений.
На Рисунках 4а, 5а и 6а приведены зависимости безразмерных частот X от угла конусности а, рассчитанные при различных значениях окружной гармоники j для разных комбинаций граничных условий, задаваемых на краях конической оболочки постоянной толщины (R/l = 2, в = 1). Приведённые данные демонстрируют значительную зависимость окружной формы колебаний с минимальной частотой от угла конусности а, особенно в случае симметричных (SS и CC) граничных условий. Для этих же граничных условий повышение угла конусности до определённого значения приводит к заметному росту минимальной частоты колебаний, что само по себе может служить очевидным конструктивным решением, направленным на максимизацию частотного спектра.
Таблица 1. К сравнению безразмерных низших частот колебаний X конической оболочки (а = 45°) постоянной толщины при различных граничных условиях
|
Окружная гармоника j |
Свободное опирание (SS) |
Жёсткое защемление (CC) |
||||||
|
[31] |
[32] |
[33] |
Расчёт |
[31] |
[32] |
[33] |
Расчёт |
|
|
1 |
0,5463 |
0,5462 |
0,5462 |
0,5462 |
0,8120 |
0,8120 |
0,8120 |
0,8119 |
|
2 |
0,6310 |
0,6310 |
0,6309 |
0,6309 |
0,6696 |
0,6696 |
0,6696 |
0,6695 |
|
3 |
0,5062 |
0,5065 |
0,5061 |
0,5061 |
0,5428 |
0,5430 |
0,5428 |
0,5427 |
|
4 |
0,3942 |
0,3947 |
0,3941 |
0,3941 |
0,4566 |
0,4570 |
0,4565 |
0,4564 |
|
5 |
0,3340 |
0,3348 |
0,3337 |
0,3337 |
0,4089 |
0,4095 |
0,4088 |
0,4087 |
|
6 |
0,3239 |
0,3248 |
0,3235 |
0,3235 |
0,3963 |
0,3970 |
0,3961 |
0,3960 |
|
7 |
0,3514 |
0,3524 |
0,3510 |
0,3510 |
0,4143 |
0,4151 |
0,4141 |
0,4139 |
|
8 |
0,4023 |
0,4033 |
0,4019 |
0,4019 |
0,4568 |
0,4577 |
0,4567 |
0,4565 |
|
9 |
0,4676 |
0,4684 |
0,4671 |
0,4671 |
0,5177 |
0,5186 |
0,5175 |
0,5173 |
Таблица 2. К сравнению минимальных частот колебаний ю (Гц) жёстко закреплённой (CC) конической оболочки переменной толщины (V2) при различных значениях углов конусности а , линейных размеров RJ1 и параметра переменности толщины р
|
а , ° |
Р |
R1 /1 = 0,5 |
R 11 = 1 |
RJ1 = 2 |
R111 = 5 |
||||||||
|
[18] |
j |
Расчёт |
[18] |
j |
Расчёт |
[18] |
j |
Расчёт |
[18] |
j |
Расчёт |
||
|
15 |
1 |
5021,83 |
9 |
5024,54 |
1815,93 |
9 |
1817,83 |
854,72 |
8 |
855,43 |
347,69 |
7 |
347,36 |
|
3 |
6280,01 |
9 |
6280,59 |
2145,69 |
10 |
2145,25 |
954,92 |
9 |
953,85 |
371,42 |
8 |
370,30 |
|
|
5 |
6842,47 |
9 |
6833,77 |
2296,27 |
10 |
2293,12 |
1005,08 |
9 |
1002,64 |
384,44 |
8 |
382,67 |
|
|
30 |
1 |
4905,77 |
8 |
4908,28 |
1677,56 |
9 |
1679,16 |
740,18 |
8 |
740,45 |
281,25 |
8 |
281,09 |
|
3 |
6158,04 |
9 |
6158,33 |
2001,63 |
10 |
2001,42 |
837,58 |
10 |
837,13 |
302,46 |
10 |
301,84 |
|
|
5 |
6717,63 |
9 |
6708,44 |
2148,51 |
10 |
2145,81 |
879,96 |
10 |
878,27 |
311,65 |
11 |
310,57 |
|
|
45 |
1 |
4763,09 |
8 |
4765,17 |
1527,07 |
8 |
1528,19 |
628,35 |
8 |
628,71 |
225,35 |
9 |
225,46 |
|
3 |
6010,19 |
7 |
6010,92 |
1844,52 |
9 |
1844,50 |
718,11 |
9 |
717,52 |
243,68 |
11 |
243,32 |
|
|
5 |
6566,66 |
7 |
6557,87 |
1988,18 |
10 |
1985,78 |
757,47 |
10 |
756,27 |
251,56 |
12 |
250,85 |
|
|
60 |
1 |
4606,77 |
6 |
4608,56 |
1368,59 |
7 |
1369,53 |
512,32 |
8 |
512,95 |
172,03 |
8 |
172,06 |
|
3 |
5848,06 |
5 |
5848,54 |
1679,73 |
8 |
1679,88 |
593,62 |
9 |
593,56 |
187,94 |
10 |
187,74 |
|
|
5 |
6403,42 |
5 |
6394,11 |
1819,28 |
8 |
1817,14 |
630,39 |
9 |
629,58 |
195,26 |
11 |
194,82 |
|
Остальные графики на рисунках 4-6 отражают влияние угла конусности а на отношение частот ю/ю0 , полученных при различных законах изменения толщины и разной величине параметра переменности р . Здесь ю — наименьшее значение в спектре частот, соответствующих нескольким окружным гармоникам. Немонотонный характер кривых в большей степени обусловлен сменой окружной гармоники с минимальной частотой колебаний. Такая трансформация может происходить как у оболочек с постоянными (и это отражается на всех кривых), так и с переменными профилями. Демонстрируемые зависимости наглядно иллюстрируют преимущества или недостатки переменного профиля по сравнению с постоянным для оболочек с разными комбинациями граничных условий и одинаковым весом при конкретном значении угла конусности.
Обобщая приведённые на рисунках 4–6 данные можно заключить:
-
1) универсального закона изменения толщины, подходящего для различных граничных условий, не существует; каждый из законов проявляет себя особым образом для той или иной конфигурации;
-
2) для некоторых законов изменения толщины, наиболее подходящих к тем или иным граничным условиям, увеличение параметра переменности р приводит к росту минимальной частоты колебаний;
-
3) для этих же законов повышение угла конусности а и связанное с ним приращение боковой поверхности оболочки приводят к значительному возрастанию минимальной частоты колебаний, особенно в случае консольного закрепления.
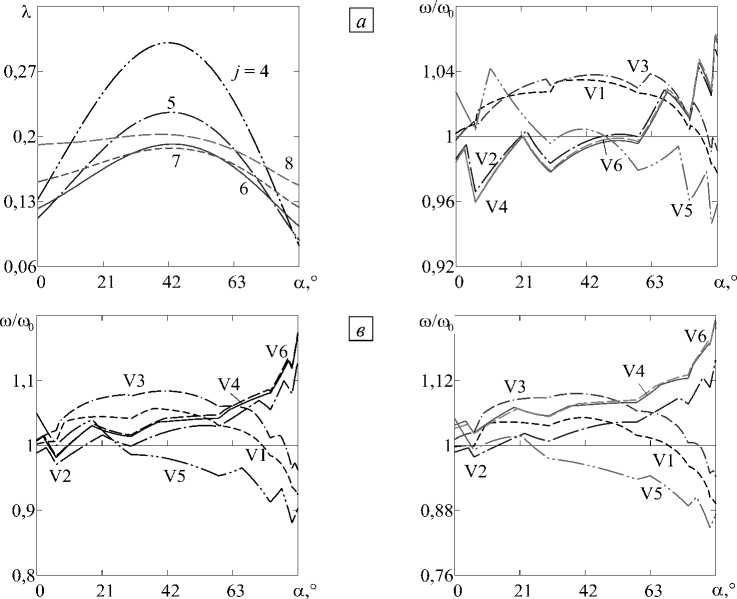
Рис. 4. Зависимости безразмерных X ( а ) и нормализованных ю/ю0 ( б )-( г ) частот от угла конусности а свободно опёртой
оболочки при значениях параметра переменности толщины в : 1 ( а ), 2 ( б), 5 ( в), 8 ( г )
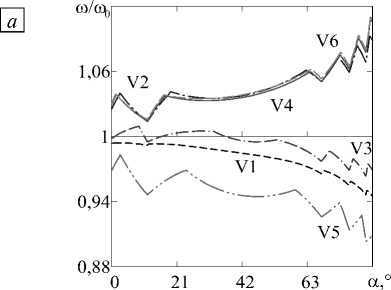
Наиболее сложная картина имеет место в случаях свободно опёртых оболочек (Рис. 4 б - г ). Здесь в определённых диапазонах значений углов конусности предпочтительнее использовать либо несимметричные профили, либо любой из симметричных. При этих же граничных условиях выпуклый гармонический профиль (вариант V5) единственным образом при 0 = 2 и узком диапазоне значений а проявляет свои преимущества относительно других конфигураций. В качестве обратного следует сослаться на работу [34], в которой показано, что для цилиндрической оболочки, нагруженной равномерной осевой силой, этот закон изменения толщины при жёстком закреплении краёв обеспечивает наиболее эффективные параметры устойчивости.
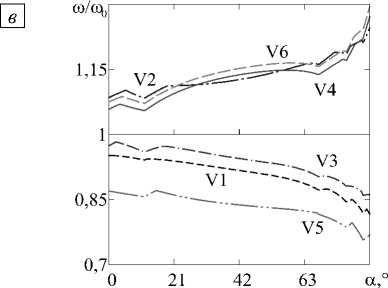
Исходя из полученных данных, можно заключить, что применимость симметричных и несимметричных профилей однозначно определяется задаваемыми граничными условиями. В случае двустороннего жёсткого закрепления (см. Рис. 5 б - г ) преимущество каждого из симметричных профилей проявляется при любом угле конусности и гарантирует повышение минимальной частоты даже по сравнению с цилиндрической оболочкой постоянной толщины. Примеры с консольным граничным условием (см. Рис. 6 б - г , закрепление осуществляется по краю с максимальной толщиной), наоборот, демонстрируют явное превосходство несимметричных вариантов изменения толщины по сравнению с симметричными. Исключение составляет лишь вариант с 0 = 5 , где профиль V4 при небольшом угле конусности более эффективен.
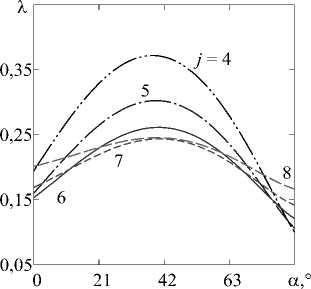
Рис. 5. Зависимости безразмерных X ( а ) и нормализованных ю/ю0 ( б )-( г ) частот от угла конусности а жёстко закреплённой оболочки при значениях параметра переменности толщины 0 : 1 ( а ), 2 ( б ), 5 ( в ), 8 ( г )
б
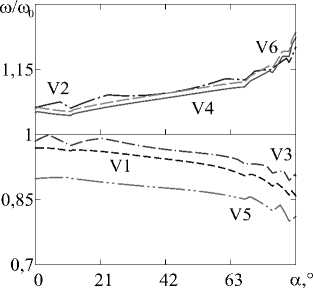
Рис. 5. Продолжение
г
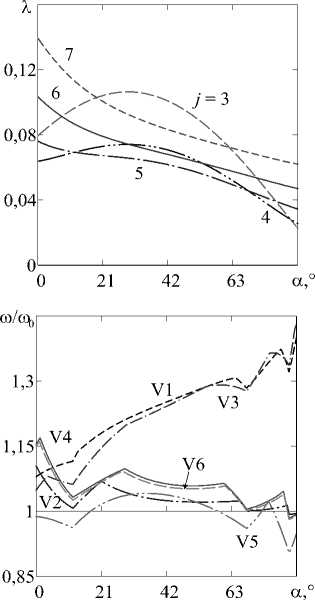
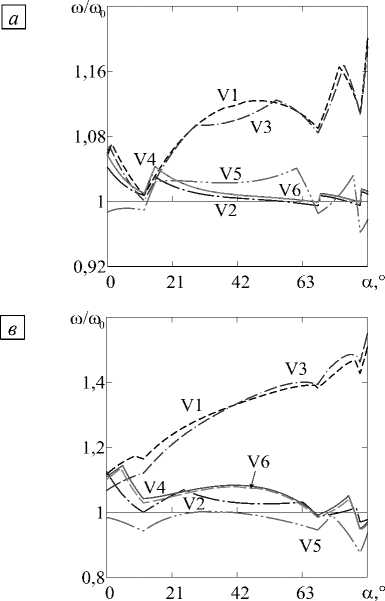
Рис. 6. Зависимости безразмерных X ( а ) и нормализованных ю/ю0
б
г
( б )-( г ) частот от угла конусности а консольно
закреплённой оболочки при значениях параметра переменности толщины р : 1 ( а ), 2 ( б ), 5 ( в ), 8 ( г )
Отметим также, что за редким исключением при таких граничных условиях переменная толщина стенки обеспечивает более высокие значения частот, по сравнению с равномерным распределением массы вдоль меридиональной координаты.
Результаты, полученные при других геометрических размерах и сведённые в таблицу 3, демонстрируют, что как для очень коротких ( Rjl = 0,5), так и более длинных оболочек ( Rjl > 5) приведённые выше зависимости не соблюдаются только при условии свободного опирания. Но, если для этих граничных условий несимметричные профили V1 и V3 уступают симметричным в случае коротких оболочек при больших углах конусности, то более длинным оболочкам они, наоборот, гарантируют повышение частоты колебаний во всем диапазоне изменения углов конусности. Более того, использование длинных оболочек с симметричным профилем становится не рациональным в связи с ухудшением характеристик по сравнению с оболочками постоянной толщины. Количественные различия в минимальных частотах колебаний оболочек с переменной и постоянной толщинами зависят как от геометрических размеров, так и от заданных граничных условий. У свободно опёртых оболочек отношение частот ю/ю0 достигает максимальных значений, если оболочка короткая: Rjl = 2, у жёстко закреплённых — при Rjl = 0,5, а в случае консольной заделки величина ю/ю0 повышается с ростом отношения Rjl .
Таблица 3. Нормализованные частоты ю/ю0 оболочки переменной толщины при различных граничных условиях
Свободное опирание (SS)
|
а , ° |
R1 // = 0,5 |
R1 Ц = 5 |
R// = 10 |
|||||||||||||||
|
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
|
|
0 |
0,992 |
1,036 |
1,002 |
1,042 |
0,957 |
1,043 |
1,000 |
0,981 |
0,995 |
0,980 |
1,020 |
0,980 |
0,997 |
0,986 |
0,994 |
0,987 |
1,007 |
0,986 |
|
0,959 |
1,095 |
0,993 |
1,125 |
0,893 |
1,121 |
0,995 |
0,955 |
0,989 |
0,964 |
1,034 |
0,961 |
0,986 |
0,948 |
0,975 |
0,934 |
1,006 |
0,943 |
|
|
0,932 |
1,105 |
0,984 |
1,035 |
0,858 |
1,031 |
0,989 |
0,936 |
0,983 |
0,956 |
1,034 |
0,950 |
0,978 |
0,920 |
0,960 |
0,929 |
1,002 |
0,921 |
|
|
15 |
0,991 |
1,042 |
1,003 |
1,049 |
0,960 |
1,050 |
1,054 |
0,967 |
1,050 |
0,958 |
1,042 |
0,959 |
1,076 |
1,001 |
1,085 |
0,996 |
1,019 |
0,998 |
|
0,957 |
1,105 |
0,992 |
1,107 |
0,889 |
1,103 |
1,105 |
0,961 |
1,123 |
0,961 |
1,035 |
0,964 |
1,149 |
1,000 |
1,197 |
0,974 |
1,042 |
0,979 |
|
|
0,931 |
1,086 |
0,982 |
1,030 |
0,854 |
1,025 |
1,111 |
0,960 |
1,150 |
0,982 |
1,027 |
0,983 |
1,169 |
0,988 |
1,209 |
0,973 |
1,048 |
0,977 |
|
|
30 |
0,988 |
1,044 |
1,001 |
1,052 |
0,955 |
1,053 |
1,061 |
0,981 |
1,064 |
0,972 |
0,996 |
0,974 |
1,092 |
1,000 |
1,097 |
0,988 |
0,990 |
0,990 |
|
0,949 |
1,104 |
0,986 |
1,095 |
0,883 |
1,090 |
1,110 |
0,982 |
1,137 |
0,960 |
0,991 |
0,965 |
1,155 |
0,945 |
1,129 |
0,911 |
0,989 |
0,914 |
|
|
0,919 |
1,071 |
0,973 |
1,045 |
0,847 |
1,039 |
1,120 |
0,977 |
1,137 |
0,965 |
0,986 |
0,969 |
1,165 |
0,927 |
1,118 |
0,889 |
0,988 |
0,894 |
|
|
45 |
0,983 |
1,050 |
0,997 |
1,060 |
0,950 |
1,061 |
1,071 |
1,008 |
1,082 |
0,997 |
1,008 |
0,998 |
1,076 |
0,975 |
1,072 |
0,964 |
0,997 |
0,962 |
|
0,933 |
1,033 |
0,972 |
1,040 |
0,880 |
1,035 |
1,124 |
0,988 |
1,125 |
0,959 |
1,005 |
0,963 |
1,115 |
0,917 |
1,081 |
0,877 |
0,959 |
0,878 |
|
|
0,902 |
1,014 |
0,954 |
1,016 |
0,839 |
1,008 |
1,132 |
0,977 |
1,114 |
0,959 |
0,987 |
0,963 |
1,118 |
0,896 |
1,062 |
0,855 |
0,943 |
0,859 |
|
|
60 |
0,976 |
1,049 |
0,990 |
1,061 |
0,952 |
1,062 |
1,066 |
1,001 |
1,071 |
0,991 |
1,000 |
0,992 |
1,058 |
0,959 |
1,047 |
0,949 |
0,987 |
0,948 |
|
0,953 |
0,988 |
0,960 |
1,005 |
0,887 |
0,999 |
1,099 |
0,977 |
1,089 |
0,952 |
0,984 |
0,956 |
1,083 |
0,901 |
1,046 |
0,865 |
0,951 |
0,867 |
|
|
0,930 |
0,973 |
0,935 |
0,993 |
0,844 |
0,984 |
1,097 |
0,968 |
1,072 |
0,955 |
0,963 |
0,959 |
1,081 |
0,882 |
1,026 |
0,849 |
0,930 |
0,852 |
|
|
75 |
0,983 |
0,956 |
0,975 |
0,962 |
1,004 |
0,959 |
1,035 |
0,993 |
1,037 |
0,984 |
0,975 |
0,986 |
1,045 |
0,966 |
1,037 |
0,956 |
0,989 |
0,955 |
|
0,923 |
0,882 |
0,898 |
0,907 |
0,949 |
0,898 |
1,045 |
0,978 |
1,039 |
0,959 |
0,952 |
0,964 |
1,057 |
0,915 |
1,025 |
0,885 |
0,954 |
0,887 |
|
|
0,888 |
0,855 |
0,855 |
0,891 |
0,907 |
0,880 |
1,035 |
0,975 |
1,019 |
0,971 |
0,940 |
0,976 |
1,047 |
0,900 |
1,001 |
0,876 |
0,941 |
0,879 |
|
Жёсткое защемление (CC)
|
а , ° |
R// = 0,5 |
R// = 5 |
R// = 10 |
|||||||||||||||
|
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
|
|
0 |
0,987 |
1,091 |
1,012 |
1,105 |
0,895 |
1,108 |
0,995 |
1,012 |
0,997 |
1,018 |
1,011 |
1,018 |
0,996 |
0,992 |
0,992 |
0,997 |
1,031 |
0,997 |
|
0,942 |
1,204 |
0,993 |
1,226 |
0,787 |
1,239 |
0,976 |
1,042 |
0,986 |
0,998 |
0,974 |
1,005 |
0,979 |
1,034 |
0,978 |
1,032 |
1,065 |
1,040 |
|
|
0,916 |
1,256 |
0,970 |
1,272 |
0,737 |
1,295 |
0,962 |
1,046 |
0,976 |
1,015 |
0,929 |
1,027 |
0,967 |
1,062 |
0,968 |
1,007 |
1,010 |
1,024 |
|
|
15 |
0,982 |
1,096 |
1,009 |
1,112 |
0,895 |
1,114 |
0,998 |
0,997 |
1,006 |
0,993 |
0,955 |
0,994 |
1,013 |
1,025 |
1,023 |
1,019 |
0,991 |
1,018 |
|
0,932 |
1,211 |
0,983 |
1,239 |
0,782 |
1,251 |
0,974 |
1,024 |
0,992 |
0,992 |
0,917 |
1,001 |
0,999 |
1,016 |
1,019 |
0,979 |
0,926 |
0,983 |
|
|
0,903 |
1,264 |
0,959 |
1,286 |
0,736 |
1,309 |
0,954 |
1,035 |
0,976 |
0,985 |
0,901 |
0,999 |
0,981 |
1,015 |
0,997 |
0,954 |
0,890 |
0,964 |
|
|
30 |
0,976 |
1,097 |
1,004 |
1,115 |
0,889 |
1,118 |
1,000 |
1,018 |
1,004 |
1,012 |
0,957 |
1,015 |
1,000 |
0,997 |
1,006 |
0,993 |
0,962 |
0,993 |
|
0,918 |
1,218 |
0,972 |
1,252 |
0,774 |
1,265 |
0,971 |
1,026 |
0,985 |
0,991 |
0,914 |
0,998 |
0,971 |
0,975 |
0,963 |
0,953 |
0,916 |
0,958 |
|
|
0,887 |
1,272 |
0,943 |
1,304 |
0,726 |
1,327 |
0,948 |
1,033 |
0,960 |
0,977 |
0,883 |
0,989 |
0,947 |
0,983 |
0,933 |
0,968 |
0,877 |
0,979 |
|
|
45 |
0,972 |
1,107 |
1,004 |
1,131 |
0,887 |
1,133 |
0,996 |
1,023 |
1,004 |
1,016 |
0,971 |
1,018 |
0,993 |
0,994 |
0,991 |
0,991 |
0,973 |
0,991 |
|
0,909 |
1,235 |
0,966 |
1,284 |
0,763 |
1,297 |
0,961 |
1,026 |
0,966 |
0,994 |
0,901 |
0,999 |
0,950 |
1,026 |
0,953 |
1,017 |
0,910 |
1,027 |
|
|
0,875 |
1,294 |
0,935 |
1,341 |
0,712 |
1,366 |
0,934 |
1,035 |
0,934 |
0,978 |
0,871 |
0,989 |
0,923 |
1,053 |
0,929 |
1,064 |
0,877 |
1,078 |
|
|
60 |
0,968 |
1,115 |
1,003 |
1,147 |
0,872 |
1,149 |
0,988 |
1,024 |
0,992 |
1,018 |
0,966 |
1,020 |
0,980 |
0,999 |
0,981 |
0,995 |
0,976 |
0,996 |
|
0,895 |
1,259 |
0,961 |
1,329 |
0,743 |
1,343 |
0,940 |
1,033 |
0,945 |
1,003 |
0,896 |
1,009 |
0,934 |
1,043 |
0,943 |
1,036 |
0,919 |
1,046 |
|
|
0,856 |
1,324 |
0,924 |
1,398 |
0,691 |
1,424 |
0,910 |
1,045 |
0,909 |
0,990 |
0,865 |
1,001 |
0,905 |
1,073 |
0,917 |
1,087 |
0,883 |
1,101 |
|
|
75 |
0,968 |
1,138 |
1,012 |
1,188 |
0,848 |
1,189 |
0,974 |
1,033 |
0,980 |
1,028 |
0,954 |
1,030 |
0,969 |
0,999 |
0,972 |
1,000 |
0,973 |
0,998 |
|
0,887 |
1,311 |
0,967 |
1,423 |
0,707 |
1,438 |
0,914 |
1,070 |
0,924 |
1,038 |
0,888 |
1,045 |
0,914 |
1,008 |
0,910 |
0,992 |
0,912 |
1,000 |
|
|
0,839 |
1,391 |
0,924 |
1,512 |
0,654 |
1,542 |
0,881 |
1,086 |
0,887 |
1,034 |
0,850 |
1,049 |
0,881 |
1,027 |
0,877 |
1,022 |
0,883 |
1,035 |
|
Консольное закрепление (CF)
|
а , ° |
R// = 0,5 |
R// = 5 |
R// = 10 |
|||||||||||||||
|
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
|
|
0 |
1,063 |
1,013 |
1,061 |
1,020 |
0,990 |
1,019 |
0,951 |
1,086 |
0,949 |
1,109 |
0,982 |
1,108 |
1,031 |
1,062 |
1,035 |
1,084 |
0,979 |
1,083 |
|
1,159 |
1,016 |
1,131 |
1,020 |
0,970 |
1,014 |
1,004 |
1,061 |
1,014 |
1,042 |
1,012 |
1,038 |
1,167 |
1,153 |
1,223 |
1,273 |
0,986 |
1,255 |
|
|
1,210 |
0,990 |
1,161 |
0,996 |
0,953 |
0,984 |
1,054 |
1,027 |
1,008 |
0,999 |
0,961 |
0,992 |
1,246 |
1,186 |
1,181 |
1,366 |
0,989 |
1,334 |
|
|
15 |
1,070 |
1,005 |
1,069 |
1,010 |
0,991 |
1,009 |
1,022 |
1,014 |
1,009 |
1,025 |
0,991 |
1,025 |
1,137 |
1,005 |
1,145 |
1,010 |
1,030 |
1,010 |
|
1,181 |
0,999 |
1,153 |
1,012 |
0,966 |
1,007 |
1,150 |
1,023 |
1,163 |
1,027 |
0,948 |
1,024 |
1,378 |
1,034 |
1,358 |
1,072 |
1,082 |
1,067 |
|
|
1,242 |
0,988 |
1,195 |
0,977 |
0,948 |
0,968 |
1,227 |
1,013 |
1,231 |
1,018 |
0,924 |
1,013 |
1,494 |
1,045 |
1,500 |
1,105 |
1,102 |
1,094 |
|
|
30 |
1,083 |
1,002 |
1,082 |
1,007 |
0,991 |
1,006 |
1,137 |
1,002 |
1,144 |
1,006 |
1,031 |
1,006 |
1,117 |
0,979 |
1,111 |
0,980 |
1,005 |
0,980 |
|
1,210 |
0,992 |
1,186 |
1,003 |
0,967 |
0,998 |
1,335 |
1,028 |
1,324 |
1,062 |
1,077 |
1,058 |
1,351 |
1,010 |
1,433 |
1,052 |
0,940 |
1,047 |
|
|
1,277 |
0,979 |
1,236 |
0,964 |
0,950 |
0,956 |
1,425 |
1,037 |
1,482 |
1,092 |
1,018 |
1,081 |
1,467 |
1,027 |
1,653 |
1,100 |
0,912 |
1,088 |
|
|
45 |
1,103 |
1,004 |
1,101 |
1,009 |
0,994 |
1,008 |
1,164 |
1,009 |
1,145 |
1,014 |
1,009 |
1,013 |
1,175 |
0,996 |
1,186 |
0,999 |
1,051 |
0,999 |
|
1,250 |
0,998 |
1,230 |
0,989 |
0,969 |
0,984 |
1,362 |
1,029 |
1,398 |
1,051 |
1,032 |
1,048 |
1,466 |
1,026 |
1,604 |
1,059 |
0,972 |
1,055 |
|
|
1,320 |
0,970 |
1,287 |
0,952 |
0,937 |
0,944 |
1,468 |
1,033 |
1,574 |
1,065 |
1,015 |
1,058 |
1,602 |
1,039 |
1,842 |
1,091 |
0,922 |
1,084 |
|
|
60 |
1,114 |
1,001 |
1,116 |
1,003 |
0,983 |
1,002 |
1,182 |
1,007 |
1,189 |
1,012 |
1,018 |
1,011 |
1,187 |
0,996 |
1,200 |
1,000 |
1,051 |
0,999 |
|
1,284 |
0,978 |
1,272 |
0,973 |
0,947 |
0,968 |
1,425 |
1,030 |
1,464 |
1,054 |
1,038 |
1,050 |
1,493 |
1,029 |
1,655 |
1,061 |
0,939 |
1,058 |
|
|
1,365 |
0,957 |
1,340 |
0,929 |
0,925 |
0,925 |
1,539 |
1,035 |
1,670 |
1,070 |
0,974 |
1,063 |
1,636 |
1,043 |
1,932 |
1,094 |
0,893 |
1,087 |
|
|
75 |
1,166 |
1,007 |
1,172 |
1,006 |
0,971 |
1,006 |
1,137 |
0,982 |
1,136 |
0,983 |
0,985 |
0,983 |
1,250 |
1,045 |
1,246 |
1,049 |
0,957 |
1,049 |
|
1,385 |
0,986 |
1,387 |
0,961 |
0,927 |
0,959 |
1,388 |
1,007 |
1,480 |
1,041 |
0,921 |
1,036 |
1,552 |
1,079 |
1,669 |
1,111 |
0,928 |
1,108 |
|
|
1,490 |
0,963 |
1,481 |
0,895 |
0,891 |
0,893 |
1,510 |
1,018 |
1,663 |
1,076 |
0,894 |
1,066 |
1,697 |
1,095 |
1,953 |
1,152 |
0,920 |
1,145 |
5. Заключение
Представлены результаты численных исследований частотного спектра усечённых круговых конических оболочек, толщина стенок которых меняется вдоль меридиональной координаты по степенному или гармоническому законам. Проанализировано влияние граничных условий, геометрических размеров, параметра переменности толщины, угла конусности на собственные частоты колебаний конструкции. Осуществлено сравнение частот, полученных для оболочек с постоянной и переменной толщинами, при условии эквивалентности их масс. Для оболочек, толщина которых является функцией меридиональной координаты, выявлено существование комбинаций, состоящих из граничных условий, закона изменения толщины с симметричным/несимметричным профилем стенки или положительной/отрицательной кривизной боковой поверхности, линейных размеров и другого, при которых имеет место значительный рост минимальных частот по сравнению с оболочкой постоянной толщины. Продемонстрировано, что для конкретных граничных условий подбором ряда параметров можно добиться существенной максимизации минимальной частоты колебаний при сохранении массы оболочки (при определённом угле конусности) неизменной.
Работа выполнена в рамках государственного задания (тема АААА-А19-119012290100-8).
Список литературы Собственные колебания усечённых конических оболочек переменной толщины
- Баничук Н.В. Оптимизация форм упругих тел. М.: Наука, 1980. 256 с.
- Hu H.-T., Ou S.-C. Maximization of the fundamental frequencies of laminated truncated conical shells with respect to fiber orientations // Compos. Struct. 2001. Vol. 52. P. 265-275.
- Blom A.W., Setoodeh S., Hol J.M.A.M., Gürdal Z. Design of variable-stiffness conical shells for maximum fundamental eigenfrequency // Comput. Struct. 2008. Vol. 86. P. 870-878.
- Topal U. Multiobjective optimization of laminated composite cylindrical shells for maximum frequency and buckling load // Mater. Design. 2009. Vol. 30. P. 2584-2594.
- Hu H.-T., Chen P.-J. Maximization of fundamental frequencies of axially compressed laminated truncated conical shells against fiber orientation // Thin-Walled Struct. 2015. Vol. 97. P. 154-170.
- Shi J.-X., Nagano T., Shimoda M. Fundamental frequency maximization of orthotropic shells using a free-form optimization method // Compos. Struct. 2017. Vol. 170. P. 135-145.
- Медведев М.Г. О максимизации основной собственной частоты и полимодальности форм колебаний ортотропных оболочек переменной толщины // Изв. АН СССР. МТТ. 1985. № 3. С. 144-148.
- Шарыпов Ф.А. Свободные колебания конических оболочек линейно-переменной толщины // Исследования по теории пластин и оболочек. Казань: Изд-во Казанского ун-та, 1970. Вып. 6-7. C. 648-655.
- Soni S.R., Jain R.K., Prasad C. Torsional vibrations of shells of revolution of variable thickness // J. Acoust. Soc. Am. 1973. Vol. 53. P. 1445-1447.
- Chandrasekaran K. Torsional vibrations of some layered shells of revolution // J. Sound Vib. 1977. Vol. 55. P. 27-37.
- Takahashi S., Suzuki K., Anzai E., Kosawada T. Axisymmetric vibrations of conical shells with variable thickness // Bull. JSME. 1982. Vol. 25, No. 209. P. 1771-1780.
- Irie T., Yamada G., Kaneko Y. Free vibration of a conical shell with variable thickness // J. Sound Vib. 1982. Vol. 82. P. 83-94.
- Takahashi S., Suzuki K., Kosawada T. Vibrations of conical shells with variable thickness (continued) // Bull. JSME. 1985. Vol. 28, No. 235. P. 117-123.
- Takahashi S., Suzuki K., Kosawada T. Vibrations of conical shells with variable thickness (3rd report, analysis by the higher-order improved theory) // Bull. JSME. 1986. Vol. 29, No. 258. P. 4306-4311.
- Sankaranarayanan N., Chandrasekaran K., Ramaiyan G. Axisymmetric vibrations of laminated conical shells of variable thickness // J. Sound Vib. 1987. Vol. 118. P. 151-161.
- Sankaranarayanan N., Chandrasekaran K., Ramaiyan G. Free vibrations of laminated conical shells of variable thickness // J. Sound Vib. 1988. Vol. 123. P. 357-371.
- Sivadas K.R., Ganesan N. Free vibration of cantilever conical shells with variable thickness // Comput. Struct. 1990. Vol. 36. P. 559-566.
- Sivadas K.R., Ganesan N. Vibration analysis of laminated conical shells with variable thickness // J. Sound Vib. 1991. Vol. 148. P. 477-491.
- Sivadas K.R., Ganesan N. Vibration analysis of thick composite clamped conical shells of varying thickness // J. Sound Vib. 1992. Vol. 152. P. 27-37.
- Viswanathan K.K., Navaneethakrishnan P.V. Free vibration of layered truncated conical shell frusta of differently varying thickness by the method of collocation with cubic and quintic splines // Int. J. Solids Struct. 2005.Vol. 42. P. 1129-1150.
- Григоренко А.Я., Мальцев С.А. О свободных колебаниях ортотропных конических оболочек переменной в двух направлениях толщины // Докл. НАН Украины. 2009. № 11. С. 60-66.
- Ning W., Zhang D.S., Jia J.L. Free vibration analysis of stiffened conical shell with variable thickness distribution // Appl. Mech. Mater. 2014. Vol. 614. P. 7-11.
- Dai Q., Cao Q., Chen Y. Free vibration analysis of truncated circular conical shells with variable thickness using the Haar wavelet method // J. Vibroeng. 2016. Vol. 18. P. 5291-5305.
- Javed S., Viswanathan K.K., Aziz Z.A., Lee J.H. Vibration analysis of a shear deformed anti-symmetric angle-ply conical shells with varying sinusoidal thickness // Struct. Eng. Mech. 2016. Vol. 58. P. 1001-1020.
- Viswanathan K.K., Nor Hafizah A.K., Aziz Z.A. Free vibration of angle-ply laminated conical shell frusta with linear and exponential thickness variations // Int. J. Acoust. Vib. 2018. Vol. 23. P. 264-276.
- Javed S., Al Mukaha F.H.H., Salama M.A. Free vibration analysis of composite conical shells with variable thickness // Shock Vib. Vol. 2020. 4028607.
- Sivadas K.R., Ganesan N. Free vibration of circular cylindrical shells with axially varying thickness // J. Sound Vib. 1991. Vol. 147. P. 73-85.
- El-Kaabazi N., Kennedy D. Calculation of natural frequencies and vibration modes of variable thickness cylindrical shells using the Wittrick-Williams algorithm // Comput. Struct. 2012.Vol. 104-105. P. 4-12.
- Кармишин А.В., Лясковец В.А., Мяченков В.И., Фролов А.Н. Статика и динамика тонкостенных оболочечных конструкций. М.: Машиностроение, 1975. 376 с.
- Годунов С.К. О численном решении краевых задач для систем линейных обыкновенных дифференциальных уравнений // УМН. 1961. Т. 16, № 3. С. 171-174.
- Irie T., Yamada G., Tanaka K. Natural frequencies of truncated conical shells // J. Sound Vib. 1984. Vol. 92. P. 447-453.
- Shu C. An efficient approach for free vibration analysis of conical shells // Int. J. Mech. Sci. 1996. Vol. 38. P. 935-949.
- Liew K.M., Ng T.Y., Zhao X. Free vibration analysis of conical shells via the element-free kp-Ritz method // J. Sound Vib. 2005. Vol. 281. P. 627-645.
- Хлопцева Н.С. Весовая эффективность тонкостенных оболочек постоянной и переменной толщины // Механика. Математика. Сб. науч. трудов. Саратов: Изд-во Сарат. ун-та., 2007. Вып. 9. С. 155-157.


