Собственные колебания вращающейся круговой цилиндрической оболочки с жидкостью

В работах [1, 2] рассматриваются собственные колебания и устойчивость вращающихся бесконечно длинных цилиндрических оболочек, внутри которых находится текущая среда, которая вращается с той же угловой скоростью, что и оболочка. В [1] установлено, что вращение оболочки с жидкостью приводит к снижению критической скорости потока по сравнению с вариантом, когда их вращение не принимается во внимание. Течение же газа, как отмечается в [2], оказывает незначительное влияние на собственные колебания вращающейся вместе с ним оболочки.

В недавно опубликованной работе [3] полученные в [1] выводы подвергаются сомнению. Было обнаружено, что в рамках используемого в [1] аналитического решения задачи невозможно математически получить неустойчивое состояние системы, когда в качестве дестабилизирующего механизма наряду с осевым течением жидкости учитывается также совместное вращение оболочки и жидкости. На основании этого вывода авторы [3] задаются вопросом о физическом смысле возникающих

математических трудностей, предполагая невозможность потери устойчивости даже в таких случаях, когда она представляется физически разумной.

В настоящей работе исследуется вращающаяся вместе с жидкостью оболочка без учета осевой скорости жидкости. В рамках численной реализации задачи представлен анализ влияния скорости вращения оболочки и/или жидкости на собственные колебания и/или устойчивость системы при различных граничных условиях, накладываемых на торцах оболочки.

Рассматривается упругая цилиндрическая оболочка длиной l , радиусом R и толщиной h . Оболочка вращается относительно своей продольной оси с угловой скоростью Q ^ . Внутри оболочки находится идеальная сжимаемая жидкость, которая вращается с угловой скоростью Q f Для описания вращающейся жидкости в области V f вводится в рассмотрение потенциал возмущения скорости ф, который в случае малых возмущений описывается волновым уравнением, имеющим в цилиндрической системе координат ( r , 0, x ) вид [4]:

_У 2 ф-1 дф_ 2^ -> ,^м № — r дф) c² 81²     c² 808t c ² (so²     8r J

где с — скорость звука в жидкости. Давление жидкости P_f на упругую конструкцию вычисляется по линеаризованной формуле Бернулли

( дф

Pf — — P     + О f      f (81 f

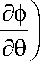
(на поверхности S _c — S_f n S₅ ).

Здесь: p _f — удельная плотность жидкости; 5 — меридиональная координата оболочки; S_f , S_s — площади, ограничивающие объемы жидкости и оболочки соответственно. На поверхности раздела оболочка-жидкость S _о задается условие непроницаемости

5ф 8 w     8 w

— —— + Q, —, 8 n    8 1    ^f д0

где n — нормаль к поверхности, w — нормальная составляющая вектора перемещений оболочки. Потенциал возмущения скорости на входе в оболочку и выходе из нее подчиняется следующим граничным условиям:

x = 0: ф — 0, x = l : 8ф]8x — 0.

Применение метода Бубнова–Галёркина к уравнению в частных производных для потенциала возмущения скорости (1) с граничными условиями (3), (4) позволяет получить систему уравнений [5]:

m

f

Zf

f

l — 1

mf

8F 8F_k 1 8F d F 8F 8F_k ^² 2

l k ^+ l k ^+ l k ^+ f

8r 8r r ² d0 d0 8x 8x cc

Z J

l — 1

V

F l F k c ²

, 2Q.f8F,

,J    ^^FdV ^ф a

Vf

^d F l F _{— r}^FkF dv ф d0^{2 k}     8 r ^k

al

+

ms X i=1

w

N F.dSx. , + Q —^F_kdSw_fli i k ai            f             k ai

S ,                 S ,       ⁵⁰

( l — 1, m s ) , ( k — 1, m f.

Здесь: m f. , m s — число конечных элементов, на которые разбиваются области жидкости V f и оболочки V s ; ф _al , w p — узловые значения потенциала возмущения скорости жидкости и перемещений оболочки; F_k , F_l, N^w — функции формы для потенциала возмущения скорости и нормальной составляющей вектора перемещения оболочки, точки над символами обозначают производные по времени.

Для классической теории оболочек, основанной на гипотезах Кирхгофа-Лява, компоненты вектора деформации в криволинейной системе координат ( s , 0, z ) могут быть записаны следующим образом [6]:

⁸ 11 = ^Еп ^{+ zk} 11 ,

⁸ 22

^Е 22 ^{+ zk} 22 ,

^Е 12 ^{+ zk} 12 ,

( ⁶ а)

где

Е_п =8 1 +120 2 , k _H = k 1 , ( 1 ^ 2 ) , Е ₁₂ =8 ₁₂ + 0 1 0 ₂ , k ₁₂ = 2т.                     (6б)

В выражениях (6) приняты обозначения:

5 u

⁸ 1 =      ,      ⁸ 2

5s

1 (5 v

R (50

5 v 1 5 u

--1--- , 5s R 50

0 1 =

5 w

5 s ’

R

-

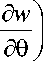
52 w k1 — 2VV , 5 s 1

.     1 (5 v

² R ² (50

w ¹

50 ² J

т—1 Г*-^ w 1

R (5 s 5 s 50 J

Здесь: u , v — меридиональная и окружная составляющие вектора перемещений; 0 _i — углы поворота недеформируемой нормали.

Компоненты оболочечных деформаций (6б) можно представить в матричной форме:

1T e — e* +—Ee, где e — {Еи,Е22,Е12,k11,k22,k12}T; e* —{81,82,812,k1,k2,2t}t — вектор линейной части деформации; e — {0,0,0,0,01,02,0,0,0}t; E — матрица линейных множителей, которая имеет ненулевые компоненты Е15 = 01, Е16 = 02, Е35 = 02, Е36 = 01. Здесь и далее индекс «Т» означает операцию транспонирования матриц.

Соотношения упругости в матричном виде записываются следующим образом:

T — { ^ 11 , T 22 , T x2 , M 11 , M 22 , M 12 } ^T — De * .

Для изотропного материала матрица D имеет ненулевые элементы: v D 11 — D ₁₂ — D ₂₁ — v D ₂₂ — v Eh] ( 1 -v ² ) ,       D ₃₃ h ²/12 — D ₆₆ — Gh ³/12,

V D 44 = D 45 = D ,4 = v D 55 = [v Eh 712 ]/ ( 1 -V ² ) .

Здесь E , v и G — модуль упругости, коэффициент Пуассона и модуль сдвига оболочки.

Энергии деформации оболочки с дополнительными слагаемыми, учитывающими предварительное нагружение, соответствует выражение:

2U = J s T De , dS + J e ^T o 0 e dS .                                                       (7)

S s S s

Матрица о ⁰, элементы которой находятся из условия E ^T De 0 = о ⁰ е , имеет ненулевые значения с ₅₅ = T 11 , с 66 = T ₂₂.

Кинетическая энергия Т оболочки, вращающейся с угловой скоростью Q s [7], вычисляется по формуле:

2T = J p s ( и ² + ( v - R Q _s -Q s w ) 2 + ( Sv + v Q s ) ² ) dV ,                                 (8)

Vs где ps — удельная плотность материала оболочки.

Выражение для работы W , совершаемой гидродинамическими силами, записывается в виде:

W = J P f wdS .                                                               (9)

S s

Далее для численной реализации используем полуаналитический вариант метода конечных элементов, основанный на представлении искомого решения в виде ряда Фурье по окружной координате 0 [6]:

и = У ” й. cos j 0 + У ” й, sin j 0 ,

Z—i j = 0 j ^J         j = 0 j ^J ’

E ”         ”

j = ₀ v sin j ⁰ E j ₀ v cos j ⁰ ,

E” -       V” - j=0 wj cos j0 + ^=0 wj sin j0

Ф a = E ”= 0 ^Ф j cos ^{j 0 +} T Tj = ₀ ^-j sin ^{j 0}

Здесь j — номер гармоники, а коэффициенты разложений (например, и j и U j ) соответствуют симметричным и антисимметричным составляющим решений соответственно.

Записывая в (10) симметричные и антисимметричные неизвестные через узловые перемещения, получим выражения для полей перемещений и потенциала в каждом конечном элементе оболочки и жидкости

U = { и , v , w } T = Nd , = [f N N ] { d , d , } ^T,                                               (11)

Ф . = Fф , =[ F F ] { Ф , Ф , } T .

Здесь N и F — матрицы функций формы, d e и ф _е — векторы узловых перемещений. Для оболочки используется конечный элемент в виде усеченного конуса с аппроксимацией меридиональной и окружной компонент вектора перемещений линейным полиномом и нормальной компоненты — кубическим полиномом. Сеточная область, соответствующая жидкости, состоит из треугольных конечных элементов с линейной аппроксимацией потенциала возмущения скорости. С учетом (11) запишем выражения, связывающие деформации с , и e с узловыми перемещениями:

6 . = Bd e , e = Gd e ,

где B и G — матрицы связи.

Для вывода уравнений движения возьмем уравнение Лагранжа d ( 5L ^ 5L dt (cdT ) 5dT

Здесь: d , d — обобщенные перемещения и скорости; L = T - U — функция Лагранжа; Q = d W /5 d ^T — обобщенные силы. Используя выражения (7-9) и учитывая (11-13), из (14) получим следующее матричное уравнение:

( K - + K g - K ; ) d + M , d + C - d +p f C T ф , + p , A ; ф, = 0.                           (15)

Здесь: K s = Z J B T DB dS — матрица жесткости; M s = Z J P ₀ N T N dS — матрица масс;

msSs ms Ss

g = Z J G T ° 0 G dS — матрица геометрической жесткости; K ^ = Z J P 0 ^ 2 N T ^ i N dS —

^m s S s

^m s S s

матрица влияния центробежных сил; C f = Z J 2 p ₀ ^ s N ^12N dS — матрица влияния сил m s S_s

Кориолиса; C „ = ZJ N T. F dS ; A f = ZJ ⁿ - ^N T. I F dS ; P o = J p s dz ; “ 123 =- 1; « 132 = 1; m s S „                        m s S „          ^d0                h

Q222 =“233 = 1 ; матрицы и векторы с верхним индексом «0» определяются из решения осесимметричной статической задачи Ksd = f , где fe = {0

Уравнение (5) с матричный вид:

учетом представлений (11),

0 p ₀ R Q 2 } ^t.

(12) принимает следующий

где

( K , + K f ) *, + M , ф

- C f ф , - C -f xw , - A f - w , = 0,

^K , = ZJ

( 5 F ^T 5 F

1 5 F ^T 5 F 5 F ^T 5 F

m f V f ⁽

5 r 9 r r ² 50 50    9 x 9 x _v

dV ,

M

K - = ZJ“- m^f V f c

2T      T

^-^ F - r ^^ F dV , 50 ²        d r

I to

ZJ mf Vf

= ZJ F T2 F dV ■ m f V c

f

2П, 5FT

—/ ^d F F dV , c ² 50

A f Хр’ f m s S ,

F dS .

Таким образом, анализ вращающейся оболочки, внутри которой вращается жидкость, сводится к совместному решению двух матричных уравнений: (15) и (16).

Объединим эти уравнения следующим образом:

( K + A ){ d Ф . } T + M { d Ф a } ^T + C { d Ф a } ^T = 0,                                  (17)

где

K =

K + K g - K ^c sss

^-p f ^{( K} f ^{+ K} / )

M _s 0

⁰   -p f ^M f

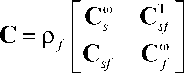
Вследствие выбранного представления (10) матрицы Cf, Cf и A являются кососимметричными. Записывая возмущенное движение оболочки и жидкости в виде d = q exp(i*Xt), фа = ф exp(i*Xt), где q, ф — некоторые функции координат, i * = V-T, а X = X1 + i *X 2 — характеристический показатель, получим окончательное выражение для объединенного решения:

( K - X 2 M + i * X C + A ) { q ф } ^Т = 0.

Таким образом, проблема исследования вращающей вместе с жидкостью оболочки без учета осевой скорости жидкости сводится к вычислению и анализу собственных значений X системы (18). Для вычисления комплексных собственных значений применяется алгоритм на основе метода Мюллера [8]. Этот метод является достаточно эффективным, поскольку не требует сведения к стандартной или обобщенной проблеме собственных значений и позволяет использовать ленточную структуру разрешающих матриц.

В приведенных далее примерах цилиндрическая оболочка характеризуется параметрами: E = 1,033 x 10 6 Н/м²; v = 0,49; p s = 1050 кг/м³; R = 1,9 х 10^-2 м; h = 3,8 х 10^-4 м. Вращающаяся с оболочкой несжимаемая жидкость имеет плотность p f = 10³ кг/м³. Все расчеты выполнены при разбиении оболочки на 40 элементов и области жидкости — на 1000.

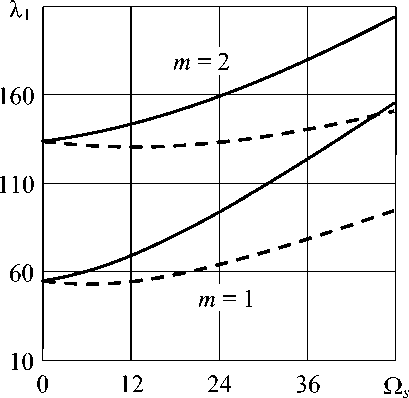
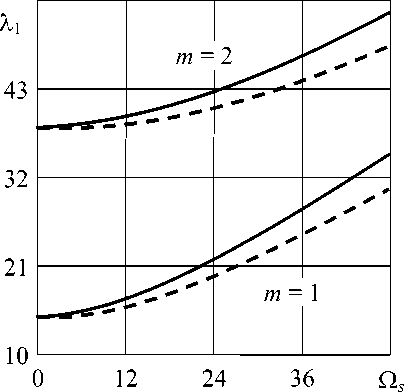
На рисунке 1, а представлена зависимость двух первых собственных частот колебаний X1 от скорости вращения Qs (об/с) пустой оболочки, свободно опертой на обоих торцах (v = w = 0, x = 0, l) при отношении геометрических размеров l/R = 2 и номере гармоники j = 3. На рисунке через m обозначено число полуволн в меридиональном направлении. При учете вращения собственные частоты расщепляются на прямую и обратную и соответствуют волнам, бегущим в разные стороны с различными скоростями [9]. Здесь, как и на последующих рисунках, обратная волна изображается сплошной линией, а прямая волна — штриховой линией.

На рисунке 1, б показана зависимость собственных частот колебаний λ 1 от скорости вращения Ω s оболочки, заполненной неподвижной жидкостью. Наличие жидкости, помимо значительного снижения собственных частот, приводит также к уменьшению различий между прямой и обратной волнами.

Рисунок 2, а демонстрирует изменение действительных и мнимых (штрихпунктирная линия) частей двух первых собственных значений λ (Гц) от скорости вращения жидкости Ω f (об/с) в неподвижной оболочке. Учет вращения жидкости также приводит к расщеплению собственной частоты колебаний. Возрастание скорости вращения жидкости способствует увеличению собственных значений, соответствующих обратным волнам, и уменьшению собственных значений, отвечающих прямым волнам. При определенной скорости вращения действительная часть прямой волны первой моды становится равной нулю, а дальнейшее увеличение скорости вызывает ее рост. При скорости вращения жидкости Ω u (критическая скорость) действительные части обеих волн первой моды сливаются и происходит появление одинаковых, но противоположных по знаку мнимых частей, что характеризует наступление потери устойчивости в виде флаттера. Этот вид потери устойчивости оболочек при слиянии прямой и обратной волны получен в [10], где исследуется стационарные оболочки, взаимодействующие с внешним вращающимся газом.

На рисунке 2, б представлена зависимость двух первых собственных частот колебаний λ 1 от скорости вращения Ω для варианта расчета, когда оболочка и жидкость внутри нее вращаются с одинаковой скоростью Ω = Ω f = Ω s . Учет вращения оболочки не оказывает существенного влияния на собственные частоты колебаний при малой скорости вращения, но с ее увеличением собственные частоты изменяются таким образом, что потери устойчивости не происходит.

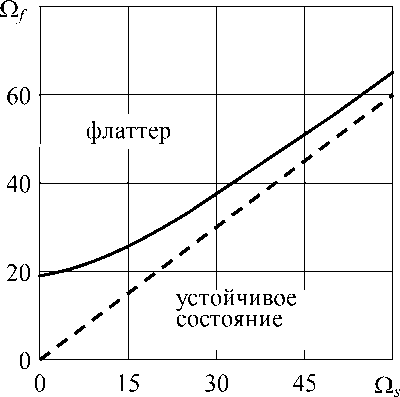
Модельные расчеты, выполненные для случая, когда оболочка и жидкость вращаются с разными скоростями (Рис. 3), позволяют оценить влияние вращения оболочки на устойчивость системы. Из результатов, представленных на рисунке 3, а , следует, что вращение оболочки оказывает стабилизирующее влияние, так как с увеличением скорости вращения для достижения потери устойчивости требуется

а

Рис. 1. Собственные частоты колебаний (Гц) пустой ( а ) и заполненной жидкостью ( б ) вращающейся свободно опертой на обоих торцах оболочки при l / R = 2, j = 3

б

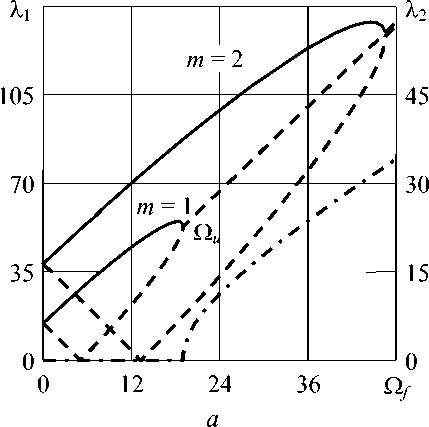
Рис. 2. Собственные частоты колебаний неподвижной ( а ) и вращающейся ( б ) свободно опертой на обоих торцах оболочки, содержащей вращающуюся жидкость

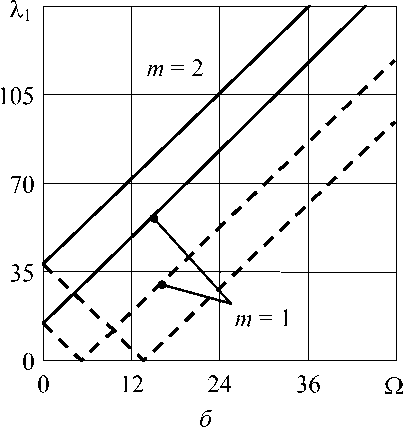
бóльшая скорость вращения жидкости. Более наглядно этот факт отражает изображенная на рисунке 3, б граница устойчивости. Здесь пунктиром показана линия, соответствующая равным скоростям вращения оболочки и жидкости, к которой стремится кривая границы устойчивости с увеличением скорости вращения оболочки. Исходя из этого, можно предположить, что только при значительных скоростях вращения оболочки можно получить такие скорости вращения жидкости, при которых система перестанет оставаться устойчивой. Таким образом, при выбранных параметрах оболочки и жидкости, вращающихся с одной скоростью, потеря устойчивости системы не может осуществиться.

В приведенных примерах вращающаяся пустая оболочка остается устойчивой (Рис. 1, а ), тогда как в работе [1] отмечается факт потери устойчивости при скорости вращения ~10 об/с. В [1] учитываются центробежные силы и силы Кориолиса, но не берутся в расчет начальные окружные усилия, вызванные центробежными силами. Такой подход был широко распространен при анализе вращающихся упругих колец и оболочек до тех пор, пока в [11] не было показано, что имеющиеся при возрастании скорости

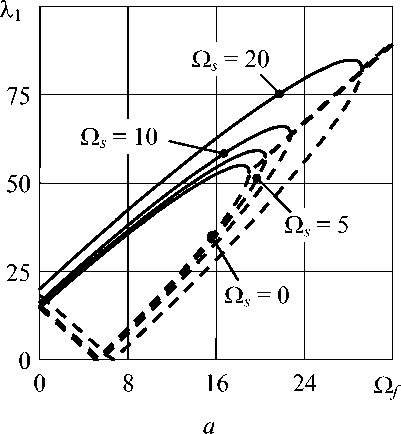
Рис. 3. Собственные частоты колебаний ( а ) и граница устойчивости ( б ) свободно опертой на обоих торцах оболочки при различных скоростях вращения оболочки и жидкости

б

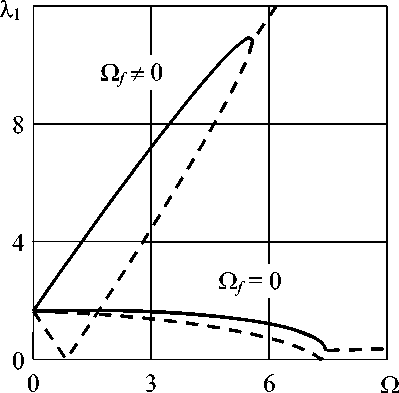
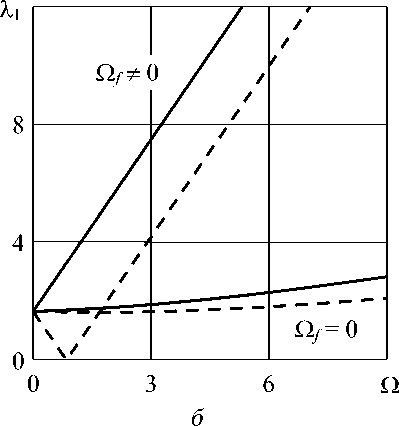
Рис. 4. Собственные частоты колебаний вращающейся свободно опертой на обоих торцах оболочки с неподвижной и вращающейся жидкостью без учета ( а ) и с учетом ( б ) начальных окружных усилий, вызванных центробежными силами при l / R = 10, j = 2, m = 1

вращения расхождения результатов вычислений с экспериментальными данными обусловлены отсутствием учета влияния именно окружных усилий. Чтобы учесть это обстоятельство в описанном выше численном алгоритме, достаточно в нем исключить из рассмотрения решение осесимметричной статической задачи.

Для сравнения с решением [1] рассматривалась более длинная оболочка ( l / R = 10), поскольку в этом случае, как и в [1], критической гармоникой (гармоника, на которой скорость вращения минимальна) является вторая. При этом критическая скорость вращения пустой оболочки составила ~12 об/с. На рисунке 4, а показаны результаты расчетов, полученные для вращающейся оболочки с неподвижной и вращающейся с такой же скоростью жидкости без учета начальных окружных усилий. В обоих случаях потеря устойчивости происходит по типу флаттера и наступает при слиянии прямой и обратной волн. Для сравнения приведены результаты аналогичных расчетов, выполненных в полной постановке (Рис. 4, б ). Из сопоставления рисунков можно сделать вывод о стабилизирующем влиянии начальных окружных усилий, вызванных центробежными силами.

Помимо свободно опертых (SS), также рассмотрены оболочки, жестко закрепленные на обоих торцах (CC) ( u = v = w = ∂ w / ∂ s = 0 при x = 0, l ), и консольно закрепленные (CF). В качестве параметра сравнения взята скорость вращения оболочки и жидкости, при которой прямая волна низшей частоты достигает нулевого значения.

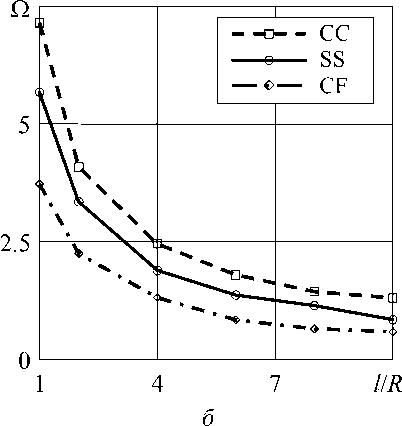
Результаты исследования оболочек с разными граничными условиями представлены на рисунке 5. Из графиков рисунка 5, а следует, что зависимость от вида граничных условий наиболее сильно проявляется в различии скоростей вращения оболочки с жидкостью на низших гармониках (на более высоких гармониках различие практически исчезает). При этом номер гармоники, соответствующий минимальной скорости вращения, также зависит от вида граничных условий, но тем меньше, чем меньше скорость вращения системы. Вне зависимости от граничных условий увеличение длины оболочки приводит к снижению скорости вращения системы, при которой прямая волна низшей частоты достигает нулевого значения (Рис. 5, б ).

Проведенные расчеты также показали, что для рассмотренных расчетных параметров учет сжимаемости жидкости не оказывает существенного влияния на собственные частоты колебаний вращающейся системы оболочка–жидкость.

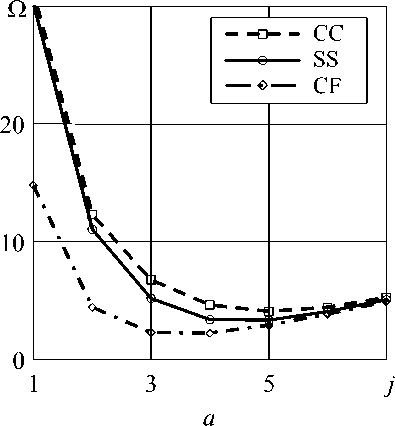
Рис. 5. Зависимость скорости вращения оболочки и жидкости Ω = Ω f = Ω _s об/с, при которой прямая волна низшей частоты достигает нулевого значения, от номера гармоники j ( l / R = 2) ( а ) и от отношения l / R ( б ) для цилиндрической оболочки при разных граничных условиях

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 09-01-00520).