Собственные значения и собственные функции оператора Лапласа в квадрате и в круге с краевым условием Вентцеля

Пусть Qc Rn , n g N\{1}, - связная ограниченная область с границей dQ класса C” дальнейшем в области Q будем искать собственные значения оператора Лапласа с граничным условием Вентцеля

A v ( x ) + lv ( x ) = 0, x g dQ , подразумевая под dQ гладкое риманово многообразие без края, с нулевым условием Неймана

— ( x ) = 0, x g Q ,

∂ n

. В

и условием непрерывности решения

Tr u = v .                                            (4)

Отметим, что хотя символом A в уравнении (1) обозначен оператор Лапласа, а в уравнении (2) - оператор Лапласа-Бельтрами, это в дальнейшем не вызовет путаницы. Более того, уравнение (2) будет рассматриваться исключительно в пространствах 0-форм. Здесь u: Q ^ R и v: dQ^R - искомые функции, параметры l, X g R, символом —обозначена производная по

∂n внешней (относительно области Q) нормали к границе dQ. В целом модель (1), (2) описывает процессы, протекающие в цитоплазме клетки и на ее мембране, и обобщает модель, предложенную в [1].

Исследование условий Коши с граничными условиями Вентцеля вида (2) впервые упоминается в работах [2, 3] при построении генератора полугруппы Феллера для многомерных диффузионных процессов в ограниченной области Q. Спустя полстолетия список математических моделей, где вместе с рассматриваемой математической моделью (2) описывает процессы на границе области Ω , существенно пополнился. В [2] этот результат был использован при решении ряда прикладных задач. Первые итоги исследований в данном направлении были подведены в [4]. Кроме того, в [5] найдены условия аналитичности разрешающих C0 -непрерывных полугрупп операторов. Наконец, в [6] рассмотрен случай, когда оператор A заменен на A2 в области Q, на границе же по-прежнему оператор Лапласа-Бельтрами А . Отметим также, что особый интерес с нашей стороны представляется в [7], где была показана неединственность разрешимости задачи с динамическим условием Вентцеля, что в дальнейшем легло в [8] при описании подходящих условий для однозначной разрешимости задачи Вентцеля–Робена для уравнения Дзекцера.

Целью нашей работы является описание свойств оператора Лапласа для уравнения Гемголь-ца с динамическим условием Вентцеля. Статья кроме введения и списка цитируемой литературы содержит два параграфа. В первом параграфе рассматриваются собственные значения оператора Лапласа с краевым условием Вентцеля (1)–(4) в круге. Во втором параграфе рассматриваются собственные значения оператора Лапласа с краевым условием Вентцеля (1)–(4) в квадрате.

Собственные значения оператора Лапласа с краевым условием Вентцеля в круге

Рассмотрим поставленную задачу (1)-(4), где в качестве области Q рассмотрим круг

KR = {(x,У): x2 + У2 - R2 } радиуса R . Перейдем к нахождению собственных значений {Xk j^ и, соответствующих им, собственных функций {фк }” для оператора Лапласа внутри круга c нулевым граничным условием Неймана, предварительно осуществив переход из декартовой системы координат в полярную. Уравнение (1) и условие (3) в полярных координатах (rф имеют вид urr (r, ф) + 1 ur (r, ф) + Л ф (r, ф) — Xu (r, ф) = 0 r          r

u_r ( R,ф) = 0.

Используя метод Фурье для данной задачи, представив решения в виде u(r,ф) = F(r)G(ф), полу- чаем следующее соотношение

F rr ( r ) + ¹ F r ( r ) — X F ( r )

r

4 F ( r )

—

^G фф ^{( ф )} =

G ( ф ) ^Y ,

r что равносильно решению двух независимых уравнений

GФФ (ф) + YG (ф) = 0, r2 Frr (r) + rFr (r) — Xr 2 F (r) = F ( r )y.

Поскольку собственная функция должна быть периодической по ф с периодом 2п, то для G(ф) получаем задачу Штурма-Лиувилля r2 Frr (r) + rFr (r) — Xr 2 F (r) = F ( r )y. G (ф) = G (ф + 2n),

решение которой имеет вид

G n ( ф ) = C 1 cos п ф + C₂ sin п ф , у = y n = n ², n e {0} uN .                    (9)

Нетрудно заметить, что второе уравнение в (7) при каждом у = п2 сводится к уравнению типа Бесселя путем следующих преобразований и замены x = r—-Х , где X < 0, r2 Frr (r) + rFr (r) — F (r )(—Xr2 + y) = 0,

В силу нашей замены x = r —X , и того, что у = п2 , преобразуем искомое уравнение в сле- дующем виде

X ^{2 F}xx ( x ) ⁺ XF x ( x ) ^{— F} ( x ⁾⁽ x ^{2 —} n ² ) = ⁰ .

Решая полученное уравнение с нулевым граничным условием Неймана, получаем собственные значения в следующем виде

( ( n ) V

_X = _X ( n ) = R ^k       R ’

Гончаров Н.С.              Собственные значения и собственные функции оператора Лапласа в квадрате и в круге с краевым условием Вентцеля где Un) - нули функции Бесселя первого порядка Jn (R --Л). C другой стороны, имеем на границе области выражение r 2 Gw (ф) F (r) + IF (r) G (ф) = 0, что равносильно уравнению

J ( 4-X R )( l - R ² n ²) = 0,

в силу того, что Tr u = v и Gфф (ф) = -n2G(ф). Решая уравнение (10) в зависимости от ограниче- ний на l имеем следующее

Утверждение 1.1 Собственные значения оператора Лапласа в круге K_R с краевым условием

Вентцеля (3) имеют вид

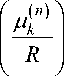
где ^ _к n ) - нули функции Бесселя первого порядка J_n (x ), если l ^ R ² n ² .

В силу (9) каждая собственная функция un

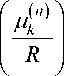
( C 1 cos п ф + C ₂ sin п ф )

будет решением уравнения (1), удовлетворяющим граничным условиям (2) и (3), а также условию непрерывности решения (4). Таким образом, общее решение задачи (1)–(4) в круге K име- ет вид

ЭД

U и ( r, ф ) = ^ —— ( Ci cos Пф + C2 Sin Пф). i, n =11 R /

Если этот ряд сходится равномерно, так же как и ряды, получающиеся из него двукратным почленным дифференцированием по r и ф , то сумма его, очевидно будет решением рассматриваемого уравнения (1). Данное утверждение легко доказывается, например, из теоремы Вейершт-расса о равномерной сходимости рассматриваемых рядов.

Собственные значения оператора Лапласа с краевым условием Вентцеля в квадрате

Рассмотрим теперь задачу (1)-(4), где в качестве области Q рассмотрим квадрат

Пп = {(x,у): (x,у)е[0,п]х[0,п]} со стороной п . Перейдем к нахождению собственных значе ний {Як }”=1 и, соответствующих им, собственных функций {фк}”  для оператора Лапласа внут ри квадрата Пп c нулевым граничным условием Неймана. Имеем,

( Я - A ) u ( x ) = 0, x е Q , на левой границе квадрата и ( 0, у ) = 0, на верхней границе квадрата и ( x , п ) = 0, на правой границе квадрата и ( п , у ) = 0, на нижней границе квадрата и ( x ,0 ) = 0.

Используя метод Фурье для данной задачи, представив решения в виде и(x, у) = X(x)Y(у), получаем следующее соотношение

X xx ^{( x} ) =; - ^{Yyy ( у} ) = п

X(x)       Y(у)    ’ что равносильно решению двух независимых уравнений

Нетрудно заметить, что поскольку рассматриваются решения в виде u(x, y) = X(x)Y(y), соб ственные функции unm (x, y) и собственные значения Xnm внутри квадрата имеют вид unm (x, y ) = cos nx cos my и Xnm =-n2 - m2 соответственно.

С другой стороны, изучая по аналогии собственные значения для оператора Лапласа на границе квадрата сП _П в силу условия на непрерывность решения (4) получим следующую систему из собственных значений и собственных функций на соответствующих сторонах П П , П П , П 3 ,

п4

X m? = - m ², u m ( x , y ) = cos my , ( x , y ) e П 1 = { ( x , y ) : x = 0,0 <  y <  n } , х П ^{2 )} = - n ², u\_m ( x , y ) = ( - 1 ) ^m cos nx , ( x , y ) e П ² = { ( x , y ) :0 <  x <  n , y = n } , хХ' = - m ², u m ( x , y ) = cos my , ( x , y ) e П 3 = { ( x , y ) : x = n ,0 <  y <  n } , ^ m ^{4 )} = - n ², u 4 m ( x , y ) = ( - 1 ) m cos nx , ( x , y ) e П 4 = { ( x , y ) :0 <  x <  n , y = 0 } . Имеет место следующее

Утверждение 2.1 Собственные значения оператора Лапласа в квадрате ПП с краевым условием Вентцеля (3) имеют вид при условии, что m = n .

Поскольку собственные числа в квадрате – сумма собственных чисел по осям, нетрудно заметим, что каждая собственная функция

• 2 ^

u_n ( x , y ) = — ^ cos nx cos ny

^П n = 1

будет решением (1), удовлетворяющим граничным условиям (2) и (3), а также условию непрерывности решения (4).

Если этот ряд сходится равномерно, так же как и ряды, получающиеся из него двукратным почленным дифференцированием по x и y , то сумма его, очевидно, будет решением рассматриваемого уравнения (1). Данное утверждение легко доказывается, например, из теоремы Вейершт-расса о равномерной сходимости рассматриваемых рядов.

Работа проводилась при финансовой поддержке Министерства науки и высшего образования Российской Федерации, грант FENU-2020-0022 (2020072ГЗ).