Сочинения Платона и Аристотеля как свидетельства о становлении системы математических определений и аксиом
Автор: Щетников Андрей Иванович
Журнал: Schole. Философское антиковедение и классическая традиция @classics-nsu-schole
Рубрика: Статьи
Статья в выпуске: 2 т.1, 2007 года.
Бесплатный доступ
Новосибирский историк математики А. И. Щетников обсуждает проблему истоков системы аксиом и определений в античной математике до Евклида. Обратив внимание на отсутствие аксиом и постулатов в современной Платону геометрии, автор обращается к проблеме определений в трудах Платона и Аристотеля, чтобы затем сопоставить прочитанное там с методами и терминологией «Начал» Евклида и высказать предположение, что при всей изощренности математики времен Платона большая часть доказательств первой книги «Начал» все-таки восходит скорее к школе Аристотеля.
Древняя математика, евклид, аксиоматизация, определение
Короткий адрес: https://sciup.org/147103247
IDR: 147103247
Текст научной статьи Сочинения Платона и Аристотеля как свидетельства о становлении системы математических определений и аксиом
1. Описание проблемы
Общепризнанно, что математика впервые приобрела вид выводной системы в Древней Греции, и что именно дедуктивный характер древнегреческих математических наук отличает их от вычислительной математики древних земледельческих цивилизаций Египта и Вавилона. Образцом такой выводной системы служат Начала Евклида, в которых на протяжении тринадцати книг все предложения систематически выводятся одно за другим по цепочке, опирающейся на небольшой начальный набор недоказуемых аксиом и постулатов, и каждая книга предваряется списком определений всех тех понятий, которые в ней впервые встречаются.
Историков математики всегда живо интересовал вопрос о том, как возникла выводная математика в Древней Греции. Как пишет об этом В. А. Янков, «переход от математики как искусства счёта к математике строгого доказательства является, говоря образно, “фазовым”, и понять, как он стал возможен, одна из важных задач не только истории математики, но и истории культуры» (Янков 1997, 201). Разного рода предположений и допущений здесь всегда хватало с избытком, зато в надёжных источниках, на которые можно было бы опереться, ощущался сильный недостаток. Дело в том, что самым ранним древнегреческим математическим текстом, дошедшим до нас целиком, а не в отдельных небольших отрывках, являются Начала Евклида, созданные около 300 г. до н. э. Все последующие античные математики, сочинения которых дошли до нас, при необходимости ссылались в своих трудах именно на Начала , а математические труды предшествующей Началам эпохи представляли для них не более чем антикварный интерес, а потому и не уцелели.
Спрашивается, на каких источниках в таком случае основаны наши знания о том, как возникла и развивалась древнегреческая выводная математика от эпохи её первоначального становления до Евклида?
Во-первых, о математиках эпохи «от Фалеса и Пифагора до Евклида» и о некоторых совершённых ими открытиях имеются свидетельства у позднейших античных авторов. Многие из этих свидетельств были переданы через книгу Евдема Родосского История геометрии , написанную в конце IV в. до н. э. и до нашего времени не дошедшую
(см. Жмудь 2002); отрывки из неё сохранились у Прокла, Симпликия и других позднеантичных авторов. И хотя наши сведения о древнегреческих математиках VI–V вв. до н. э. по большей части отрывочны, всё же по этим отрывкам можно попытаться составить себе картину той науки, которой они занимались, связав фрагменты между собой и заполнив некоторые лакуны. Такого рода реконструкциям, в частности, посвящён ряд интересных, хотя не бесспорных статей В. А. Янкова (1997, 2000, 2001, 2003).
Во-вторых, отдельные отрывки из работ древних математиков до нас всё-таки дошли. В позднеантичных комментариях сохранился текст Гиппократа Хиосского (конец V в. до н. э.), посвящённый построению квадрируемых луночек, и принадлежащее Архиту Тарентскому (начало IV в. до н. э.) решение задачи удвоения куба. Из этих отрывков видно, что за век до Евклида древнегреческие математики ставили и решали весьма сложные геометрические задачи.
В-третьих, стараниями историков математики установлено, что многие книги Начал Евклида были созданы в более раннюю эпоху и включены Евклидом в его систему почти без изменений или после небольшой переработки. О. Беккер (Becker 1936) показал, что одним из таких древних фрагментов является восходящее к пифагорейцам учение о чётных и нечётных числах, завершающее IX книгу. Б. Л. Ван дер Варден (1959) приписал Архиту авторство заметной доли предложений VIII книги Начал , а также ряд арифметических теорем из Деления канона – сочинения по теории музыки, входящего в евклидовский корпус. Весьма древними являются II книга, посвящённая приёмам так называемой геометрической алгебры, и примыкающие к ней теоремы XIII книги о делении отрезка в среднем и крайнем отношении, необходимые для построения правильного пятиугольника. Авторство X книги, в которой строится классификация иррациональностей, и XIII книги, в которой излагается теория правильных многогранников, приписывается Теэтету Афинскому (начало IV в. до н. э.), а Евдокс Книдский (ок. 405–355 гг. до н. э.) считается автором теории пропорций, изложенной в V и VI книгах, и метода исчерпывания, представленного в XII книге.
В-четвёртых, обширный математический материал, непосредственно связанный с предшествующей Евклиду эпохой и пришедший к нам напрямую, а не через позднеантичных посредников, содержится в сочинениях величайших античных философов – Платона (427–347 гг. до н. э.) и Аристотеля (384–322 гг. до н. э.). Не занимаясь математикой профессионально, оба мыслителя живо интересовались состоянием современных им математических наук. Их сочинения содержат многочисленные отрывки, так или иначе связанные с математикой; и зачастую оба автора поясняют свои философские рассуждения заимствованными из матема- тики примерами (собрания отрывков из диалогов Платона, имеющих отношение к математике, см. Brumbaugh 1954, Frajese 1963, Щетников 2006; аналогичные отрывки из сочинений Аристотеля собраны в книге Heath 1949).
Подводя предварительные итоги, можно сказать, что материал по истории древнегреческой математики от Фалеса до Евклида является достаточно разнообразным, но в то же время весьма отрывочным. Поэтому в работе с этим материалом приходится применять метод историко-математических реконструкций.
Однако на этом пути нас подстерегают многочисленные подводные камни, главным из которых является изменение общей парадигмы математического мышления, произошедшее за два с половиной тысячелетия, прошедших со времени зарождения древнегреческой математики. Характерная особенность многих современных реконструкций состоит в том, что их авторы уже в силу своего образования, полученного в современной школе и университете, проявляют склонность к историческим аберрациям, неявно и наивно полагая, что математика прошлого в идейном смысле была схожей с математикой наших дней.
По отношению к деталям математических доказательств эта установка по своему существу конечно же верна: мы понимаем рассуждения Архита и Гиппократа, как если бы они были нашими современниками, ибо логика их рассуждений – та же самая, что и наша. И если бы они где-то ошиблись, то их ошибки были бы видны не только нам, но, при некоторой внимательности, и им самим.
Однако предположение об идейном единстве математики разных эпох может перестать работать, когда речь заходит не о деталях отдельных математических доказательств, но о критериях и канонах, касающихся математической науки в целом, её целей и оснований. Ведь ниоткуда не следует, что общепринятые парадигмы современной математики были всегда столь же значимы и для математики прошлого.
Поясним это утверждение на примере. Уже из школьного учебника геометрии мы узнаём, что курс геометрии положено предварять списком аксиом, из которых будут выводиться все последующие теоремы, а также перечнем определений. Знаем мы и то, что так были устроены и Начала Евклида. Отсюда может возникнуть предположение, что системы выводной математики всегда строились по одному и тому же канону, разворачиваясь от явно выставленных аксиом к последовательно выводимым из них теоремам. К примеру, в I томе Истории математики с древнейших времён до начала XIX столетия, в статье о ранней пифагорейской геометрии, сказано: «Мы не знаем, какие геометрические предложения пифагорейцы выбрали в качестве исходных и насколько велика была эта первая система аксиом» (с. 67).
Аналогичные фразы можно найти и во многих других книгах по истории математики, где они стали чем-то вроде общего места. Стало быть, здесь по умолчанию предполагается, что если пифагорейцы строили геометрию как систему связанных между собой доказательных предложений, то эта система обязательно начиналась с некоторых аксиом, поскольку так должна быть устроена всякая выводная система. Но насколько это предположение является обоснованным? В какой мере мы можем ожидать от математиков пифагорейской школы следования канонам, известным нам по математическим работам более позднего времени?
Рассмотрению этих вопросов как раз и посвящена настоящая статья. Опираясь на свидетельства Платона и Аристотеля, я постараюсь показать, что хотя древнегреческая математика второй половины V в. до н. э. и представляла собой развитую доказательную науку, тем не менее она вполне обходилась без определений и без аксиом, и что древнегреческие математики стали давать определения математических объектов лишь в первой половине IV в. до н. э., а выделять аксиомы и постулаты в качестве исходных первоначал математического знания – ещё позднее, во второй половине IV в. до н. э. Такое положение дел может сначала показаться удивительным, но когда свыкаешься с ним, начинаешь понимать, что оно как раз и является естественным: ведь когда математики открывают для себя возможность устанавливать и доказывать сложные изощрённые факты, их деятельность сперва устремляется именно в этом направлении, а требование объяснять и обосновывать всё, приводящее к попыткам установления основ доказательного знания на философском и на предметном уровне, возникает лишь на одном из следующих шагов развития науки.
2. Отсутствие «аксиом» и «постулатов» в современной Платону геометрии
Самые ранние диалоги были написаны Платоном вскоре после смерти Сократа в 399 г. до н. э., а самые поздние – в конце жизни. В диалогах Платон, по его собственным словам, передаёт «речи Сократа, когда он, ещё молодой, был прекрасен» ( Второе письмо 314c). Действие Парменида , в котором Сократ представлен совсем молодым человеком, относится к 449 г. до н. э., а действие большинства остальных диалогов – к последним трём десятилетиям V в. до н. э. При этом события последнего десятилетия V в. до н. э. Платон мог описывать по памяти, поскольку с Сократом он познакомился в 407 г. до н. э., а всё, что происходит в других диалогах раньше этого срока, могло быть известно ему по рассказам самого Сократа и других знакомых с ним людей (хотя, конечно, все эти рассказы сильно дополнялись воображением Платона).
Естественно считать, что в связанных с математикой отрывках диалогов отражены как воспоминания Платона о геометрии и арифметике времён его собственной юности, так и те проблемы, которые обсуждались математиками платоновской Академии в зрелые годы жизни Платона. Если Платон возвращается к одному и тому же математическому сюжету из диалога в диалог – надо думать, что этот сюжет был для него как-то значим; а если он ни разу не касается некоторых тем, вряд ли эти темы его занимали. (Конечно, второе допущение выглядит более шатким, нежели первое.)
В отношении обсуждаемой нами проблемы прежде всего отметим, что Платон в своих диалогах ни разу не употребляет слова ἀξίωμα в привычном нам значении специального логического термина. Оно встречается у него всего несколько раз в обыденном значении «почести», «доброй славы» ( Пир 220е, Протагор 337e, Государство 495d). И только в поздних Законах (690ad, 714d) «аксиомы» осмысливаются как некие первоначала, – но не логические, а именно ценностные, – когда обсуждаются основания власти (ἀξιώματα ἀρχῆς) и ставится вопрос: «в силу каких оснований одни должны править, а другие подчиняться?». В списках Начал Евклида аксиомы названы κοιναὶ ἔνοιαι – «общие понятия». Это словосочетание у Платона также нигде не встречается.
Кроме аксиом, Начала Евклида предваряются также списком геометрических постулатов, αἰτήματα. В обыденной речи αἴτηματα – это «допущение» или «требование»; у Евклида оно стоит в глагольной форме ἠιτήσθω – «требуется». Платоном слово αἴτημα употребляется также всего один раз, когда речь идёт о требованиях, предъявляемых тираном к народу ( Государство 566b).
Похоже, что для Платона общая логическая проблема «начал умозаключения» ещё не была значимой, так же как для математиков этого времени не была значимой специальная проблема «начал математического умозаключения»; скорее всего, никому из них даже не приходило в голову задумываться о таких началах. Так что всякие разговоры о том, что некая система аксиом имелась ещё у геометров пифагорейской школы, представляются нам беспочвенными. И хотя мы не можем этого проверить, но всё-таки с большой степенью правдоподобия мы можем утверждать, что в первых Началах , созданных Гиппократом Хиосским в конце V в. до н. э., никакого списка аксиом и постулатов не было. Тем более его не было в ещё более ранних геометрических сочинениях, вплоть до гипотетического Предания Пифагора – первого систематического сочинения по геометрии, созданного в пифагорейской школе (см. Ван дер Варден 1959, 163).
Конечно, это наше утверждение не означает, что в геометрических доказательствах пифагорейцев не присутствовали доводы, включённые впоследствии Евклидом в список аксиом, такие как «если от равных отнять равные, то и остатки будут равны», или «если две величины порознь равны третьей, то они равны и между собой», – ведь геометрических доказательств без таких доводов вообще не бывает. Однако верно и то, что эти доводы не осмысливались пифагорейцами в качестве особых «начал доказательства», предшествующих самому доказательству. Ведь для такого осмысления древним грекам пришлось создать специальную науку – логику, то есть сделать то, что первым совершил Аристотель, у которого само доказательство как таковое стало предметом научного рассмотрения.
3. Диалоги Платона и проблема определений
В отличие от проблемы «начал доказательства», перед Платоном не стоявшей, проблема «правильных определений» была для него одной из важнейших. Действие большинства диалогов Платона как раз в том и состоит, что Сократ своими вопросами подводит собеседника к необходимости дать ответ на вопрос: «Что есть то, о чём идёт речь?» В Федре (237bc) прямо говорится о том, что всякое правильное обсуждение следует начинать с определения обсуждаемого предмета:
«Всякое правильное обсуждение, о юноша, начинается с одного: надо выяснить, что именно обсуждается, иначе во всём будут неизбежны ошибки. Большинство людей не замечает, что им неизвестна сущность того или иного предмета. И словно они с ней знакомы, они не уславливаются о ней в начале рассмотрения, а это обязательно сказывается в дальнейшем: они противоречат сами себе и друг другу».
Аристотель в Метафизике (1078b17–25) утверждает, что именно Сократ первым стал искать общие определения, выражающие суть вещи:
«Сократ исследовал нравственные добродетели и первый пытался определять общее (ὁρίζεσθαι καθόλου) в них. Ведь из физиков только Демокрит касался этого и некоторым образом определил тёплое и холодное; а до этого пифагорейцы делали это для немногого, словесные объяснения (λόγοι) чего они сводили к числам, указывая, например, что такое удобный случай, справедливость или супружество. А Сократ с полным основанием искал суть вещи, так как он стремился делать умозаключения, а начало умозаключения – это суть вещи».
Интересно, что Сократ в диалогах Платона неоднократно приводит математические определения в качестве образцов для определения как такового. Так, в Меноне (74b–76a) он просит своего собеседника объяснить, что представляет собой добродетель. Но тот плохо понимает, как можно найти «единую добродетель», не улавливая самый смысл задаваемого вопроса. Тогда Сократ переводит обсуждение в другую плоскость и задаёт вопрос из геометрии: «Что это такое, включающее в себя закруглённое и прямое, – то, что ты именуешь фигурами, утверждая, что закруглённое и прямое – фигуры в равной мере?» В результате обсуждения появляется определение: «фигура – это край тела», и это определение становится образцом для определения как такового, после чего разговор возвращается к поискам определения добродетели.
В Пармениде (327e) даются следующие определения закруглённого и прямого:
«Закруглённое есть то, края чего повсюду одинаково отстоят от середины... А прямое – то, середина чего заслоняет оба края».
Что всякое определение представляет собой соединение имени предмета и его словесного объяснения, Платон разъясняет в VII письме (342bc):
«“Круг” – это нечто произносимое, и его имя – то самое, которое мы произнесли. А его словесное объяснение составлено из имён и глаголов. “То, края чего повсюду одинаково отстоят от середины” будет словесным объяснением того, что носит имя “закруглённого”, “окружности” и “круга”».
В Законах (895de) в качестве ещё одного примера приводится определение чётного числа: «число, делящееся на две равные части». Своеобразное определение чётного числа приведено также в Евтифроне (12d):
«Если бы ты спросил меня, какою частью числа будет чётное и что оно собой представляет, я ответил бы, что это число, не хромое на одну ногу, но равнобедренное».
Впрочем, при сравнительном чтении сократических диалогов Платона и Ксенофонта возникает ощущение, что определениями математических предметов как любопытным и важным для его философии новшеством интересовался не Сократ, а Платон, – и этот свой интерес он приписал Сократу как главному действующему лицу своих диалогов. Может статься, что исторический Сократ никогда не рассматривал ма- тематические определения в качестве образцов для этических определений: во всяком случае, Сократ в диалогах Ксенофонта этические определения постоянно обсуждает, но никакого интереса к математике не выказывает (поскольку такого интереса не проявлял и сам Ксенофонт).
Далее, в Государстве Платона (510cd) содержится недвусмысленное указание на то, что греческие математики конца V века обходилась в своих занятиях вообще без определений. Обращаясь к своему собеседнику, Сократ говорит так:
«Я думаю, ты знаешь, что те, кто занимается геометрией, вычислениями и тому подобными занятиями, предполагают чёт и нечет, фигуры, три вида углови прочее в таком же роде родственным всякому пути, считая его известным, принимая в качестве предположения (ὑποθέσεις) и не давая словесного объяснения (λόγον) ни себе, ни другим, словно они оценивают (ἀξιοῦσι) его как и без того всем ясное. Исходя из этого, они разбирают уже всё остальное и последовательно доводят до конца то, что было предметом их рассмотрения».
Принятая среди математиков практика, описанная в этом отрывке, не должна нас удивлять. Названия специальным математическим предметам безусловно давались и прежде, как это делают, к примеру, Феодор и Теэтет в диалоге, названном по имени последнего (147d–148d), когда они договариваются числа, которые можно получить перемножением двух одинаковых множителей, называть квадратными, прочие же – продолговатыми. Но в этом и подобных ему случаях происходило не определение предмета, а его именование: «будем называть вещь с таким-то свойством таким-то именем». Выражения «квадратное число» и «продолговатое число» сами по себе ничего не говорят новичку в математике, и ему надо специально объяснять, что они означают в качестве технических терминов. И совсем иной будет ситуация, когда вещь и её имя нам давно известны, а мы пытаемся выразить суть вещи в её словесном описании. Что такое «круглое» и «прямое», знает и новичок в геометрии, причём он знает это до всякого научного рассмотрения предмета, но предложение объяснить словами, что эти сущности собой представляют, вызывает обычно сильные трудности: знать-то мы знаем, а вот выразить своё знание в слове оказывается не так просто.
Отсюда проистекает интерес Платона к проблеме словесных определений как одной из составляющих общей проблемы знания, специально обсуждаемой в Теэтете: можно ли считать, что человек, который не способен объяснить, что такое «круглое» и «прямое», по-настоящему знает это? По-видимому, в душе у такого человека имеется некий смутный образ «круглого» и «прямого», с которым он сверяет свои впечатления; но правильное мнение, которое опирается лишь на восприятие и не может быть выражено в словах, ещё не является настоящим знанием.
Вернёмся теперь к приведённому выше свидетельству Аристотеля, в котором говорится, что до Сократа определения пытались давать пифагорейцы и Демокрит. Пифагорейские определения, о которых говорит Аристотель, нам известны по ряду позднейших текстов. Звучали они наподобие следующего: «справедливость есть способность возвратить равное и должное, содержащая в себе середину первого квадратного нечётного числа» ( Теологумены арифметики 37 1–4 ); особой глубиной математической мысли эти определения, как видно, не отличались.
Больший интерес представляет указание на то, что Демокрит (ок. 460–380 до н. э.), давал определения физическим понятиям, в частности – тёплому и холодному.
Известно, что Платон был с Демокритом в весьма натянутых отношениях. Имени Демокрита в своих сочинениях он ни разу не упоминает. Однако в диалогах Платона имеются такие развороты мысли, которые несомненно восходят к Демокриту. Один из этих разворотов, содержащийся в речи Сократа из диалога Теэтет (201e–202c), имеет непосредственное отношение к нашей теме.
«Я слышал от каких-то людей, что первые элементы (τὰ πρῶτα στοιχεῖα), из которых состоим мы и всё остальное, не имеют объяснения. Каждый из них сам по себе можно только именовать, но ничего сверх того нельзя добавить – ни того, что он есть, ни того, что его нет. Ибо тогда ему приписывалось бы бытие или небытие, а здесь нельзя ничего привносить, коль скоро высказываются только о нём одном. И к нему не подходит ни «само», ни «то», ни «каждое», ни «одно», ни «это», ни многое другое в том же роде. Ведь хотя все эти обычные слова и применяются ко всему, они всё же отличаются от того, к чему прилагаются; и если бы его можно было объяснить и он имел бы своё особое объяснение, его пришлось бы объяснять без всего прочего. Но ни один из них нельзя выразить в слове, ведь им дано лишь именоваться, иметь какое-то имя. А вот состоящие из них вещи и сами сплетаются, и имена их, также сплетаясь, образуют объяснение, сущность которого заключается именно в сплетении имен. Таким образом, эти элементы необъяснимы и непознаваемы, но лишь ощутимы. Сложное (συλλαβάς) же познаваемо, выразимо и доступно истинному мнению. И если кто составляет себе о чём-то истинное мнение без объяснения, его душа владеет истиной об этом, но не познаёт; ведь кто не может дать или получить объяснение чего-то, тот этого не знает. Получивший же объяснение может все это познать и в итоге иметь его в качестве знания».
«Какие-то люди» здесь не названы по имени, но в них бесспорно узнаются Демокрит и его последователи. Употребляемая в этом отрывке терминология опирается на аналогию со звуками речи (это и есть первоначальное значение слова στοιχεῖα) и состоящими из них слогами (συλλαβά). Звукам речи можно дать имена («альфа», «бета», «гамма» и т. д.), но их нельзя объяснить, суть каждого из них усваивается только через чувственное восприятие. А вот слоги как сочетания букв допускают объяснение: «ба» = «бета-альфа», «аб» = «альфа-бета», причём именно в таком порядке.
Даже если сам Демокрит прилагал своё воззрение только к чувственно воспринимаемым вещам, ясно, что перенос его на математические предметы был вполне возможен. Этот перенос и осуществили те геометры, которые по примеру Сократа (и, возможно, по почину Платона) стали спрашивать о математических предметах, что они суть такое, иначе говоря, стали искать для них определений. «Что такое квадрат? – Это четырёхугольник с равными сторонами и прямыми углами. – А что такое четырёхугольник? – Это фигура, граница которой образована четырьмя прямыми, соединяющими четыре точки. – Что такое граница? – Это край фигуры. – А что такое прямой угол? – Это угол, равный своему смежному. – А какие углы будут смежными? – Те, у которых одна сторона общая, а две другие лежат на одной прямой. – А что такое угол? – Это наклонение двух линий друг к другу. – И дальше: а что такое линия? что такое прямая? что такое точка?»
Интересно то, что заявленная Демокритом программа возведения всех определений к простейшим неопределимым сущностям, которые могут быть только названы по имени, но не определены, в позднейшей греческой математике не была реализована. Неоднократно отмечалось, что многие определения Евклида, такие как определения точки, линии, прямой, поверхности, плоскости, тела (I.1–7 и XI.1–2) и некоторые другие, являются логически не действующими, поскольку их содержание никак не используется в тех доказательствах, где появляются соответствующие понятия. В «программе Демокрита» эти простейшие геометрические сущности, «из которых всё состоит», следовало бы объявить неопределимыми. Возможно, что причина отклонения «программы Платона» от «программы Демокрита» заключается в том, что точка и линия, с которыми имеют дело геометры, в отличие от звуков «а» и «б», не являются предметами ощущения. Ведь точка не есть маленькое пятно (каковой её, между прочим, считал Демокрит), и линия не есть узкая полоска. Стало быть, о них нельзя сказать, что они «непознаваемы, но лишь ощутимы». Но поскольку геометры используют в своих рассуждениях такие «внечувственные» объекты, тем самым они каким-то образом знают их, и потому они должны уметь выразить сущность этих объектов в словесном объяснении, пусть даже и отрицательном: «точка есть то, что не имеет частей», «линия есть длина без ширины».
Отметим ещё одну сторону дела, связанную с математическими определениями у Платона. Определения математических объектов в Началах Евклида во многих случаях почти дословно воспроизводят аналогичные определения у Платона: таковы определения фигуры, круга, чётного числа. А «оптическое» определение прямой в Пармениде Платона (327e) – «прямое есть то, середина чего заслоняет оба края» – в значительной степени проясняет смутное определение Начал Евклида: «прямая линия есть та, которая лежит точками равно по отношению к себе».
В научной литературе неоднократно указывалось на то, что Евклид не уделил списку определений I книги Начал достаточного внимания, включив в него определения таких понятий, которые не встречаются нигде далее. В опр. 8 вводится общее понятие плоского угла, однако общий криволинейный угол нигде не рассматривается. В опр. 19 прямолинейные фигуры называются по числу сторон (τρίπλευρα, τετράπλευρα, πολύπλευρα), а в самом тексте Начал Евклид всегда обозначает их по числу углов (τρίγωνα, τετράγωνα, πολύγωνα). В опр. 22 производится классификация четырёхсторонних фигур, но вводимые здесь термины ἑτερόμηκες (наш прямоугольник), ῥόμβος, ῥομβοειδές (наш параллелограмм) и τραπέζια (любой четырёхугольник общей формы – не путать с нашей трапецией!) нигде далее не используются, поскольку в дальнейших предложениях Евклид называет ромбоид – параллелограммом, а прямоугольник – прямоугольным параллелограммом.
П. Таннери на основании этих наблюдений пришёл к предположению, что сводный каталог математических определений был составлен предшественниками Евклида, у которых он многое заимствовал в готовом виде (Tannery 1884). Д. Д. Мордухай-Болтовской считал, что определения I книги в конечном счёте восходят к Началам Гиппократа Хиосского (Евклид, I, 245).
Упомянем также противоположную точку зрения, высказанную Л. Руссо (Russo 1998), согласно которой определения математических сущностей (всех или по крайней мере некоторых, к которым относятся первые семь определений I книги) вообще не содержались в первоначальном тексте Начал , но были добавлены к нему при позднейшем редактировании с чисто учебной целью.
4. Аристотель о математических определениях
Аристотель в своих логических трудах обсуждает проблему определений весьма обстоятельно, пытаясь подвести под неё необходимый фундамент. Программа построения определений изложена им в конце
Второй Аналитики . Первым делом выдвигается требование: определение должно быть речью, выражающей суть вещи. Тем самым возникает обоснованный вопрос: а чем такая речь отличается от всякой другой речи, описывающей эту же самую вещь? Далее, лучшим представляется такое определение, которое раскрывает причину существования вещи; характерный математический сюжет на эту тему имеется в трактате О душе (413a13–20):
«Определение должно показать не только то, чем предмет является, но оно должно заключать в себе и выявлять причину. Сейчас же определения – это как бы выводы из посылок. Например, что такое квадрирование? Превращение разностороннего прямоугольника в равный ему равносторонний. Такое определение есть лишь вывод из посылок. Утверждающий же, что квадрирование есть нахождение средней, указывает причину действия».
В целом Аристотель следует программе, намеченной Платоном, а потому он предлагает строить определения путём подразделения рода на виды, причём таким образом, чтобы каждое деление осуществлялось не произвольно, но в некотором «сущностном» порядке. Однако такая программа утопична, поскольку никаких «сущностных свойств вещей» в абсолютном смысле не существует. Представим себе, что мы хотим произвести разделение рода многоугольников на виды. Должны ли мы первым делом поделить этот род на бесконечное число видов по числу сторон? А может быть, будет удобнее выделить в один общий вид все правильные многоугольники – ведь у этих многоугольников есть такие общие свойства, которых у других многоугольников нет? Диэрезис, улавливающий единичное понятие в сеть двоичных делений, может идти разными путями, как показал Платон в Софисте . Похоже, что Аристотель и сам видел неразрешимые трудности, возникающие при реализации этой программы (см. Родин 2003), но отступать от неё всё-таки не хотел.
Сочинения Аристотеля содержат немало замечаний о конкретных математических определениях. Значительная часть этих замечаний представляет собой философское брюзжание по поводу «неправильности» того или иного определения. Приведём в качестве примера отрывок из Топики (142b7–19):
«Ошибаются, когда один из противостоящих членов деления определяют через другой, например нечётное – как на единицу большее чётного. Ибо всегда по природе противостоящие члены деления будут из одного рода, а нечётное и чётное противостоят друг другу, ибо они оба – различия в числе. Так же ошибаются, если вышестоящее определяют через нижестоящее, например чётное – как число, которое делится надвое... Ведь “надвое” взято от “двух”, то есть от чётного... И тот, кто говорит “надвое”, подразумевает “чётное”, так как делить на два – значит делить надвое, а два – чётное число».
Нетрудно понять, что математики не обращали на подобные замечания ровным счётом никакого внимания. Дело в том, что никакой содержательной математической проблемы за этими замечаниями не стояло. Математик даёт чёту и нечету рабочие определения и двигается вперёд, раскрывая свойства чётных и нечётных чисел и получая о них новые знания. Пока на этом пути не обнаружится никаких камней преткновения, непосредственно связанных с содержанием принятых определений, отвлекаться на размышления о «правильности» определений у математика нет никакой нужды. Этим размышлениям могут предаваться методисты, ищущие лучшего пути изложения математики в учебниках, – но к математике как поиску новых знаний они не имеют никакого отношения.
Никакой «проблемы определений» в математике не возникало по большому счёту до XIX в., когда интуитивные представления о некоторых математических сущностях впервые оказались недостаточными для того, чтобы удерживать предмет мысли. Вот тогда-то и пришлось вернуться к вопросу Сократа: «что есть то, о чём идёт речь?» К примеру, нам кажется интуитивно ясным, что всякая непрерывная функция имеет производную почти во всей области своего определения, за исключением разве что отдельных точек; но давайте попробуем разобраться, что мы называем непрерывной функцией, и что – производной? Разобрались – и выяснили, что понятия непрерывности и дифференцируемости соотносятся друг с другом совсем не так, как это нам представлялось, и что могут существовать такие непрерывные функции, которые нигде не имеют производной.
Вся эта тематика детально обсуждается в замечательной книжке Имре Лакатоса Доказательства и опровержения (Лакатос 1967); роль проблемы определений в становлении математического анализа и теории функций действительного переменного рассматривается также в нашем обзоре (Щетников & Щетникова 1999).
5. Аксиомы у Аристотеля и общие понятия у Евклида
Платон, как мы уже отмечали, об аксиомах ничего не говорит; и похоже, что он о таких логических сущностях никогда не думал. Напротив, для философии Аристотеля тема первоначал выводного знания – одна из самых значимых. Показателен в этом отношении следующий отрывок из Второй аналитики (76a31–b22):
«Я называю началами (ἀρχάι) в каждом роде те, о чём нельзя доказать, что они существуют. Следовательно, значение первых и тех, что за ними, принимается. То, что они существуют, о началах необ- ходимо принять, прочее следует доказать. Например, что такое единица или что такое прямое и треугольник, следует принять; что единица и величина существуют, также следует принять, прочее – доказать.
Из тех [начал], которые применяются в доказательной науке, одни специфичны для каждой науки, другие являются общими (κοινά); причём они общи по аналогии, как применимые каждый раз внутри того рода, который относится к данной науке. Специфично – то, что линия такова и прямое таково; общее же – то, что если от равного отнять равное, то остается равное. Каждое из таких [начал] применимо внутри рода, ибо оно будет иметь ту же силу, даже если взять его не для всего, а лишь для величин, в арифметике же – для чисел.
Но имеются специфичные [начала], о которых полагают, что они есть, и которые наука рассматривает как существующие сами по себе, каковы единицы в арифметике, а в геометрии – точки и линии. Здесь принимается и то, что они существуют, и то, каковы они есть. Относительно же присущих им свойств принимают, что каждое из них означает; например, арифметика – что такое нечётное или чётное, или квадрат, или куб, геометрия – что такое иррациональное или кривизна, или наклон; но что всё это существует, доказывают посредством общих [начал] из уже доказанного. Точно так же и в учении о небесных телах. В самом деле, всякая доказывающая наука имеет дело с тремя сторонами: то, что полагается существующим (а именно род, свойства которого, присущие ему сами по себе, исследует наука); общие [начала], называемые аксиомами (τὰ κοινὰ λεγόμενα ἀξιώματα), из которых как из первых ведется доказательство; третье – это свойства, значения которых принимают. Ничто, однако, не мешает иным наукам некоторыми из этих сторон пренебрегать, как, например, не указывать, что род существует, если это и так ясно (ведь не в одинаковой мере ясно, что существует число и что существуют холодное и тёплое), и не указывать значения свойств, если они ясны; точно так же, как не рассматривают общезначимое, что значит отнять равное от равного, как известное. Но тем не менее по природе вещей имеются эти три: о чём доказывается, что доказывается, и из чего доказывают».
Итак, аксиомы у Аристотеля – это общие начала умозаключения, свойственные не какой-то одной, но всем доказательным наукам. Список таких начал возглавляет требование невозможности противоречия. Как сказано в Метафизике (1005b20–34):
«Самое достоверное из всех начал – то, относительно которого невозможно ошибиться... А именно: невозможно, чтобы одно и то же в одно и то же время было и не было присуще одному и тому же в одном и том же... Все, кто приводит доказательство, сводят его к этому положению как к последнему: ведь по природе оно начало даже для всех других аксиом».
Характерные примеры общих начал умозаключения, применимых во всех математических науках, представляют собой такие доводы, как «если от равного отнять равное, то и остатки будут равны» или «если две величины порознь равны третьей, то они равны и между собой». Аристотель в Метафизике (1061b17–25) указывает на то, что исследованием таких начал ни одна частная математическая наука заниматься не может, поскольку они общи им всем:
«Хотя математик и пользуется общими [началами] на свой лад, но его начала подлежат рассмотрению первой философии. Ведь [начало] “если от равного отнять равное, то остатки будут равны” является общим (κοινόν) для всякого количества, а математика производит рассмотрение, применяя его к части своего материала, будь то к линиям, к углам, к числам или к другому количеству, но не как к сущему, а как к непрерывному в одном, двух или трёх протяжениях».
Эта же мысль повторяется в Метафизике (1077b17–23) ещё раз:
«Общие [начала] (τὰ καθόλου) в математике относятся не к тому, что существует отдельно от величин и чисел, но именно к ним, однако не поскольку они имеют величину или делимы».
Не следует смешивать общие начала, о которых говорит Аристотель, с аксиомами современных математических теорий. Аксиомы в современном понимании являются исходными недоказуемыми утверждениями о неопределимых объектах теории и отношениях между ними, и совокупность аксиом выступает здесь в качестве развёрнутого определения этих объектов и отношений; а общие начала Аристотеля играют роль стандартных правил вывода, в соответствии с которыми делаются некоторые умозаключения (ср. Яновская 1958, 79). Однако эти правила вывода находятся в ведении не логики, но собственно математики.
В качестве примера использования одного из таких правил рассмотрим доказательство теоремы «два параллелограмма на общем основании и под одной высотой равны по площади». Пусть на основании AB под одной высотой построены параллелограммы ABCD и ABEF (рис. 1). Несложно показать, что треугольники DAF и CBE равны по двум сторонам и углу между ними. Заметим теперь, что если от трапеции ABED отнять треугольник CBE, остатком будет параллелограмм ABCD; а если от трапеции ABED отнять треугольник DAF, остатком будет параллелограмм ABEF. Но если от равных величин отнять рав- ные, то и остатки будут равны; поэтому параллелограммы ABCD и ABEF равны по площади.
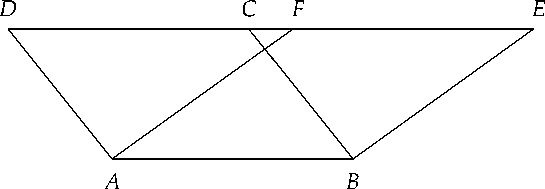
Рис. 1
Конечно же рассуждения такого рода регулярно проводились уже в ранней пифагорейской математике; и речевые формулы, подобные выделенной, были отшлифованы их многократным употреблением. Но, произнося эти формулы и производя определённые манипуляции с материей геометрического доказательства, никто не обращал внимания на сами эти формулы как на особую составляющую доказательства; ведь заметить очевидное не так просто. Выделение слоя этих формул, как особого инструмента доказательных математических рассуждений, является заслугой Аристотеля.
Рассмотрим теперь предваряющий I книгу Начал Евклида список «общих понятий» (κοιναὶ ἔνοιαι), как он приведён в редакции Гейберга. Легко видеть, что эти общие понятия вполне соответствуют аксиомам у Аристотеля. Так что разница здесь заключается единственно в названии.
1. Равные одному и тому же равны и друг другу.
2. И если к равным прибавлены равные, то равны и целые.
3. И если от равных отняты равные, то равны и остатки.
4. И если к неравным прибавлены равные, то неравны и целые.
5. И удвоенные одного и того же равны друг другу.
6. И половины одного и того же равны друг другу.
7. И совмещающиеся друг с другом равны друг другу.
8. И целое больше части.
6. Постулаты у Евклида и Аристотеля
Аксиомы с четвёртой по шестую Гейберг считал позднейшими вставками, так как они имеются не во всех рукописях Начал. Впрочем, в самом тексте Начал содержатся такие предложения, которые на эти аксиомы могли бы ссылаться. Всё же здесь следует сделать небольшую оговорку. А именно, в современных изданиях Начал в доказательствах теорем и решениях проблем имеются ссылки на предыдущие предложения, а также на исходные аксиомы и постулаты. Но эти ссылки были расставлены Гейбергом, а в исходном тесте Начал их не было. В некоторых случаях отсылка к определённой аксиоме не вызывает сомнений, поскольку в доказательстве воспроизведена её буквальная формулировка. Но когда формулировка не воспроизведена явно, мы можем увидеть отсылку к аксиоме там, где сам автор доказательства этой отсылки не видел.
Ещё одна, девятая аксиома «две прямые не охватывают пространства» выглядит в этом списке утверждений, относящихся к «равному и неравному», настолько неуместной, что я не стал её в него включать. Ведь она относится не к «величинам вообще», но только к геометрическим объектам. В ряде списков Начал её тоже нет, так что Гейберг не считал её подлинной. А Герон в Определениях (134, 1–2) поместил её и в список аксиом, и в список постулатов. Думается, что именно в последнем списке ей и надлежит находиться, так что мы обсудим её несколько ниже.
Седьмая аксиома «совмещающиеся друг с другом равны друг другу» относится только к геометрии, а не ко всем математическим наукам; однако внутри геометрии она остаётся «общей» ровно в том смысле, какой вкладывался в это слово Аристотелем, ибо она приложима ко всем непрерывным величинам. Евклид применяет её крайне редко и почти всегда неудачно. В предложении I. 4 эта аксиома используется при доказательстве признака равенства треугольников по двум сторонам и углу между ними. Впрочем, приведённое там доказательство трудно назвать состоятельным; и не случайно Д. Гильберт в Основаниях геометрии принял этот признак равенства треугольников за недоказуемую аксиому. Кроме того, на основе этой аксиомы в предложении III. 24 доказывается теорема о равенстве сегментов, отрезанных от круга равными хордами. Это доказательство опять-таки совершенно несостоятельно и никак не связано с определением равных сегментов.
Можно считать также, что в предложениях I. 6, I. 34, I. 35 эта же аксиома обеспечивает переход от поэлементного равенства треугольников к равенству их площадей. Полная схема рассуждения при этом выглядит так: «выполняется один из признаков равенства треугольников ^ треугольники совпадают при наложении ^ треугольники [как плоские фигуры] равны».
Восьмая аксиома «целое больше части» непосредственно в этом виде используется в предложениях I. 7, I. 16, I. 18, I. 20. Кроме того, в I. 6, I. 14, I. 26 Евклид пользуется стереотипным оборотом «меньшее равно большему, что нелепо». Соотношение обеих формулировок аксиомы обсуждается в статье А. Сабо (1959).
Помимо рассмотренного выше списка общих понятий, I книга Начал Евклида предваряется также списком пяти постулатов (αἴτημα = «допущение», «требование»), из которых два последних в некоторых рукописях Начал фигурируют не как постулаты, но как 10-я и 11-я аксиомы.
П1. Допустим, что от всякой точки ко всякой точке можно провести прямую линию.
П2. И ограниченную прямую можно непрерывно продолжать по прямой.
П3. И со всяким центром и раствором можно начертить круг.
П4. И все прямые углы равны между собой.
П5. И если прямая, падая на две прямые, образует внутренние односторонние углы, меньшие двух прямых, то эти две прямые, продолженные неограниченно, встречаются с той стороны, где углы меньше двух прямых.
Аристотель во Второй аналитике (76b30–34) приводит следующее определение постулата:
«Если нечто принимают, в то время как изучающий не имеет никакого мнения об этом или имеет противоположное мнение, то допускают (αἰτεῖται) это... Ибо допущение (αἴτημα) есть нечто противоположное мнению изучающего, которое, будучи доказуемым, принимается и применяется без доказательства».
Пять постулатов Евклида вряд ли могут быть названы допущениями в аристотелевском смысле. Прежде всего, их трудно счесть «противными мнению изучающего»: кто станет сомневаться в том, что точки можно соединять прямыми, и что циркулем можно проводить окружности? Далее, первые три постулата вряд ли кому-то придёт в голову пытаться доказывать. Стало быть, смысл «допущения» у Евклида совсем другой, нежели у Аристотеля.
Первые три постулата ограничивают способы построения геометрических фигур применением циркуля и линейки. Выделение этих постулатов, возможно, восходит к астроному и математику Энопиду Хиосскому (середина V в. до н. э.), исследовавшему простейшие задачи на построение. Можно сказать, что эти постулаты являются началами всякого построения с помощью циркуля и линейки (а все рассматриваемые в Началах построения именно таковы), подобно тому как аксиомы являются началами всякого доказательного рассуждения.
Перейдём теперь к оставшимся постулатам, включив в их список также девятую аксиому.
А9. Две прямые не охватывают пространства.
Иначе говоря, через две точки проходит только одна прямая. Эта аксиома используется в доказательствах предложения I. 4 (признак равенства треугольников по двум сторонам и углу между ними, доказываемый наложением) и ряда предложений XI книги (XI. 3, XI. 7).
А10 = П4. Все прямые углы равны между собой.
Прямой угол определяется у Евклида как равный смежному с ним. Мы могли бы определить его как половину развёрнутого угла, что по сути дела то же самое. Правда, для Евклида наш развёрнутый угол – это не угол вовсе, так как две прямые, образующие угол, должны быть наклонены друг к другу. Поэтому Евклид говорит не о развёрнутом угле, а о «двух прямых углах». Но если проанализировать теоремы, в которых Евклид пользуется этим постулатом, становится понятным, что доказательство этих теорем опирается именно на равенство между собой всех развёрнутых углов. Эта аксиома используется в I. 14 (если составить вместе два прямых угла, то их внешние стороны будут лежать на одной прямой) и в I. 15 (теорема о равенстве вертикальных углов).
7. Постулат о параллельных
А11 = П5. Если прямая, падая на две прямые, образует внутренние односторонние углы, меньшие двух прямых, то эти две прямые, продолженные неограниченно, встречаются с той стороны, где углы меньше двух прямых.
Это знаменитый 5-й постулат, сыгравший огромную роль в развитии геометрии, от открытия пифагорейцами теоремы о сумме углов треугольника до возникновения неевклидовых геометрий. История 5го постулата после Евклида подробно освещена в книге Б. А. Розенфельда (1976). А нас в этой статье интересует вопрос о том, когда этот постулат был принят древнегреческими математиками за одно из начал геометрического знания.
Логические проблемы, связанные с учением о параллельных, неоднократно упоминаются в сочинениях Аристотеля. В одном месте Первой Аналитики (64b36–65a7) сказано следующее:
«Когда познаваемое не через самое себя пытаются доказать через самое себя, тогда допускается изначальное (αἰτεῖται τὸ ἐξ ἀρχῆς) <…> Так поступают те, кто думает, что они проводят параллельные: ведь они неявно принимают нечто такое, что не может быть доказано, если параллельные не существуют».
И, несколько ниже (66a11–15):
«В том, что одно и то же ложное вытекает из многих предположений, равно нет ничего невозможного. К примеру, параллельные встречаются, и если внутренний угол больше внешнего, и если треугольник имеет больше двух прямых углов».
В первом отрывке приведён пример логического круга: «Те, кто думает, что они проводят параллельные, неявно принимают нечто такое, что не может быть доказано, если параллельные не существуют».
Но что именно делают «те, кто думает, что проводят параллельные», и каков смысл фразы «если параллельные не существуют»?
Второй отрывок (и некоторые другие) содержит оборот «параллельные встречаются». Но как могут встречаться параллельные прямые? Ведь у Евклида параллельные прямые не встречаются по самому их определению:
Параллельные суть прямые одной плоскости, которые, будучи продолжены неограниченно в обе стороны, ни с какой из сторон не встречаются друг с другом.
Можно предположить, что геометры из первого отрывка, проводя параллельные прямые, проводили их под равными соответственными углами к третьей прямой. Но в чём тогда смысл критики, которую ведёт Аристотель? По-видимому, в том, что при выполнении такого построения сразу же считалось интуитивно очевидным, что проведённые прямые не встречаются. «Вы не можете называть построенные прямые параллельными, – возражает на это Аристотель, – пока не докажете, что они действительно не встречаются при продолжении».
Выставленные определения не должны быть избыточными, то есть они не должны включать в себя того, что может быть доказано. Избы- точное определение параллельных прямых, с которым, как я предполагаю, Аристотель полемизирует в первом отрывке, могло звучать так: «Параллельные прямые суть те, которые при их продолжении не встречаются ни с какой стороны и образуют с секущей равные накрестлежа-щие углы». Здесь не говорится ни о том, что (1) если прямые не встречаются, то они образуют с секущей равные накрестлежащие углы, ни о том, что (2) если прямые образуют с секущей равные накрестлежащие углы, то они не встречаются. Такое определение следует понимать лишь в том смысле, что существуют параллельные прямые, которые и не встречаются, и образуют с секущей равные накрестлежащие углы.
Прокл в Комментарии к I книге «Начал» Евклида (3792-16) сообщает со ссылкой на Евдема Родосского, автора первой Истории геометрии, что пифагорейцы доказывали теорему о сумме углов треугольника следующим образом:
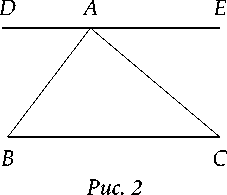
Пусть будет треугольник ABC и пусть через A будет проведена DE, параллельная BC. Так как прямые BC и DE параллельны и накрестлежащие углы равны, то, следовательно, угол DAB равен углу ABC, а угол EAC – углу ACB. Прибавим общий угол BAC. Следовательно, углы DAB, BAC, CAE, то есть углы DAB, BAE, то есть два прямых угла равны трём углам тре- угольника. Следовательно, три угла треугольника равны двум прямым.
Исходно это рассуждение могло восприниматься как полноценное доказательство, опирающееся на очевидные факты. Проблемы появляются вместе с вопросом: «А как вы будете проводить прямую DE , чтобы она была параллельна BC ?» Если ответить: «Мы проведём её так, чтобы угол DAB был равен углу ABC », то тогда встаёт ещё один вопрос: «А откуда вы знаете, что и угол EAC будет равен углу ACB ?» Если последует ответ: «Но ведь BC и DE – параллельные прямые», то следующий вопрос будет таким: «А какое определение параллельных прямых вы даёте? Если вы говорите, что параллельные прямые – это те, которые пересекают какую-нибудь одну секущую под равными накрестле-жащими углами, то вам следует доказать, что они пересекают под равными накрестлежащими углами и любую другую секущую. Если же вы говорите, что параллельные прямые – это те, которые не встречаются при продолжении, то вам следует связать свойства прямых не встречаться при продолжении и образовывать с секущей равные накрестле-жащие углы двумя взаимно обратными теоремами».
Часто задаются вопросом, почему Евклид придал постулату о параллельных такую форму (ведь предложение «через точку вне данной прямой проходит только одна прямая, параллельная данной» выглядит более простым и тем самым более подходящим на роль аксиомы). Один из возможных ответов на этот вопрос таков.
Центральную часть учения о параллельных прямых у Евклида составляют два взаимно обратных предложения I. 27 и I. 29:
I. 27. Если прямая, падающая на две прямые, образует с ними равные накрестлежащие углы, то эти две прямые параллельны друг другу.
I. 29. Прямая, падающая на две параллельные прямые, образует с ними равные накрестлежащие углы.
При доказательстве этих предложений естественно было исходить из двух взаимно обратных предпосылок. Для предложения I. 27 такой предпосылкой послужило предложение I. 16:
I. 16. Внешний угол треугольника больше несмежного с ним внутреннего угла.
Этому последнему предложению может быть придана и такая форма: «если из точки на прямую падают две прямые, при этом получаются внутренние односторонние углы, меньшие двух прямых». Обращение этого предложения как раз и приводит к формулировке пятого постулата. При этом Евклиду удалось свести предложение I.16 к ещё более простым допущениям, а обратное ему предложение – не удалось. В результате это обратное предложение и было принято за постулат о параллельных.
Подытоживая сказанное, я рискну высказать предположение о том, что значительная часть материала I книги Начал Евклида была разработана только в школе Аристотеля, а к предшествующей эпохе из теорем I книги относится лишь небольшая часть теорем неочевидного содержания (таких, как теорема о сумме углов треугольника и ряд теорем о равновеликости плоских фигур).
Конечно, геометрия эпохи Платона была весьма изощрённой в конструктивном плане, но конструктивная изощрённость не ведёт автоматически к изощрённости рефлексивной. Принято думать, что «совсем элементарная геометрия» (куда входят признаки равенства треугольников, теоремы о том, что сумма двух сторон треугольника больше третьей, и т. п.) была уже сделана «до Платона». Но существенно более правдоподобным представляется утверждение о том, что она ещё не была сделана.
Список литературы Сочинения Платона и Аристотеля как свидетельства о становлении системы математических определений и аксиом
- Ван дер Варден Б. Л. (1959) Пробуждающаяся наука: математика Древнего Египта, Вавилона и Греции. Пер. И. Н. Веселовского (Москва: Физматгиз)
- Евклид (1949-50) Начала. Пер. и коммент. Д. Д. Мордухай-Болтовского при ред. участии И. Н. Веселовского и М. Я. Выгодского. В 3 т. (Москва: ГТТИ)
- Жмудь Л. Я. (2002) Зарождение истории науки в античности (Санкт-Петербург: РХГИ)
- История математики с древнейших времён до начала XIX столетия (1970). В 3 т. (Москва: Наука)
- Лакатос И. (1967) Доказательства и опровержения: как доказываются теоремы. Пер. И. Н. Веселовского (Москва: Наука)
- Родин А. В. (2003) Математика Евклида в свете философии Платона и Аристотеля (Москва: Наука)
- Розенфельд Б. А. (1976) История неевклидовой геометрии: развитие понятия о геометрическом пространстве (Москва: Наука)
- Сабо А. (1959) "О превращении математики в дедуктивную науку и о начале ее обоснования", Историко-математические исследования 12, 321-392
- Теологумены арифметики (2007) Пер. В. В. Бибихина и А. И. Щетникова (Новосибирск: АНТ)
- Щетников А. И., Щетникова А. В. (1999) Роль контрпримеров в развитии основных понятий математического анализа (Новосибирск: АНТ)
- Щетников А. И. (2006) "Диалоги Платона как источник сведений по ранней античной математике", Academeia: Исследования и материалы по истории платонизма. Вып. 6 (Санкт-Петербург: Изд-во СПбГУ)
- Янков В. А. (1997) "Становление доказательства в ранней греческой математике (гипотетическая реконструкция)", Историко-математические исследования 2 [37], 200-236
- Янков В. А. (2000) "Гиппас и рождение геометрии величин", Историко-математические исследования 5 [40], 192-222
- Янков В. А. (2001) "Геометрия последователей Гиппаса", Историко-математические исследования 6 [41], 285-318
- Янков В. А. (2003) "Геометрия Анаксагора", Историко-математические исследования 8 [43], 241-267
- Яновская С. А. (1958) "Из истории аксиоматики", Историко-математические исследования 11, 63-96
- Becker O. (1936) "Die Lehre vom Geraden und Ungeraden in neunten Buch der Euklidishen Elemente", Quellen und Studien zur Geschichte der Mathematik, Astronomie und Physik, B 3, 533-553
- Brumbaugh R. S. (1954) Plato's Mathematical Imagination: The Mathematical Passages in the Dialogues and their Interpretation (Bloomington: Indiana UP)
- Frajese A. (1963) Platone e la matematica nel mondo antico (Rome: Studium)
- Fukagawa H., Pedoe D. (1989) Japanese Temple Geometry Problems (Winnipeg: Charles Babbage Research Foundation)
- Heath T. L. (1949) Mathematics in Aristotle (Oxford: Clarendon Press)
- Russo L. (1998) The definitions of fundamental geometric entities contained in Book I of Euclid's Elements, Archive for History of Exact Sciences 52, 195-219
- Tannery P. (1884) "Sur l'authenticié des axiomes d'Euclide", Bulletin des sciences mathématiques 8, 162-175


