Social Network Clustering

Published Online December 2013 in MECS DOI: 10.5815/ijitcs.2014.01.09

Many datasets can be represented as graphs or networks that network nodes can be seen as individuals and edges represent relationships between pairs of individuals. For example, in a telecommunication network, nodes are phone numbers and edges show that two nodes communicate or the World Wide Web (WWW) can be represented as a very large graph where nodes represent web pages and edges represent hyperlinks between pages. Community mining which has achieved more attention in recent past few years in sociology and data mining, focuses on detection and characterization of such network structure [1].

Recently, with the arising of sites such as MySpace, Friendster, Orkut, Twitter, Facebook, etc. social networks have reached major popularity and another reason of social networks popularity is that they are easy to use. These networks make people of all over the world able to communicate with each other [2]. One of the common features of these networks is called community structure which represents connected groups (clusters) that there should be many edges within each group and few between the groups. Resulted groups are fraction of individuals that have similar features or connected via relations. Groups in social networks are corresponding with social relations and are used for understanding the data structure such as organization structures, scientific collaboration and relations in telecommunication networks [1].

Community detection is useful in real networks because it is more likely that nodes in one community have same properties. Community detection methods in social networks are similar to graph partitioning, for example in parallel computation, if n computer connected processes exist that is required to distribute on g computer processors, Processes are not connected essentially and connection pattern that is needed can be represented as a graph or network which nodes are processes and edges connect pairs of processes that are needed to connect. The problem is allocating processes to processors such that in general, load is balanced on each processor while in same time the number of edges between processors is minimized such that the amount of inter processor communication is maximized. In general finding a solution for partitioning task is NP-hard [3].

Because of networks ability to modeling the many of complicated real world systems, studying them is an up-to-date research topic. A social network can be modeled as a graph G=(V,E) where V is a set of individuals that is called node or vertex and E is a set of links that is called edge and connects two elements of V [4].

Communities are useful in many applications. Web clients clustering (community detection) which have same or similar interests or are near together via location can improve the World Wide Web services performance. One of the community detection benefits is to provide better recommendation systems for efficient customer’s guidance and increasing the business opportunities via representing the lists of retailer items which produces the clusters of customers with similar interests. The goal of graphs community detection is the identification of modules and their hierarchical structure by using the information which is encoded in graph topology [5].

The problem of finding communities in social networks has been revealed recently and several metrics for evaluating community structure have been proposed [6][7][8]. Among them modularity Q is the most accurate [9]. Modularity is a criterion for evaluating the quality of partitioning a network into clusters [10].

Q is proposed by Newman and Girvan [6]. Suppose a particular division of network to k communities, this can be represented by a k×k symmetric matrix e which each element eij is the fraction of all network edges that link vertices in group i to group j. Trace matrix Tr(e) represents a fraction of network edges that connect the vertices in a group and obviously a good division has a high value of Tr(e). Although this value alone is not a good measure of the quality, because placing all vertices in a single group would give the maximal value 1 whereas no information of community structure is provided.

a^ is the expected fraction of edges within community i when the edges were distributed randomly on the network.

Q = £(e/-a2) = Tr(e)-He2 H              (1)

Where ║e║ is the sum of matrix e elements. Values of Q that are close to 1 represent a better community structure. Q usually falls in the range from 0.3 to 0.7 [8].

Figure 2 shows a small example. For a clustering of the graph in this figure which has five vertices and two clusters C 1 ={V 1 ,V 2 } and C 2 ={V 3 ,V 4 ,V 5 } . The e ij values are the sums of matrix elements belonging to a pair of C_i and C j divided by total sum of all matrix elements: e₁₁= 2/11, e₁₂= 2/12, e₂₁= 2/12, e₂₂= 4/12. The modularity of clustering the example graph into two clusters is Q=(e_n - a^ ((e₂₂ - a )==( (2/12) - (5/12)² ) + ( (4/12) - (7/12)² )=- (1/72) . The negative value of Q clearly shows a suboptimal partition. Assigning the vertex V₃ to C₁ improves Q to 1/9 [11].

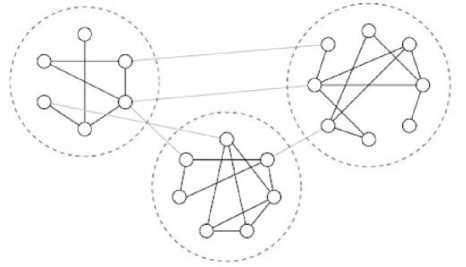
Fig. 1: A small network with three communities, represented by the dashed circles [6]

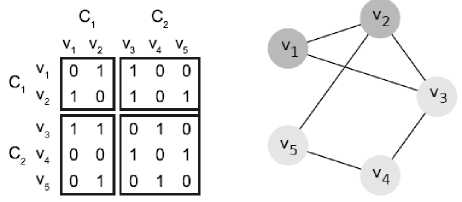
Fig. 2: Example graph [11]

The aim of this paper is clustering social networks with a better community structure and modularity. The remainder of this paper is organized as follow: Section

2 and 3 discuss the related work and proposed method recursively. In section 4 the experimental results are shown.

• II.    Related Work

Finding communities in complex networks is revealed recently by many authors. Researchers proposed different methodologies for finding such communities in various fields like physics, statistics and data mining. In this section some of the previous methods are noted.

The first analysis of community structure was represented by Weis and Jacobson in 1955; they searched for work groups in a government agency and studied the matrix of working relationships between members of the agency which were identified by interviews, groups were produced by removing the members which were working with different groups persons, because they made connections between them. The idea of removing the connections between groups is the basis of many community detection algorithms.

Earlier than the work mentioned above, in 1927 Stuart Rice searched for clusters of people which have similar voting patterns. Two decades later, George Homans showed that social groups could be revealed by rearranging the rows and the columns of matrices identifying social ties, until they take an approximate block-diagonal form. This procedure is now standard. Traditional techniques to find communities in social networks are hierarchical and partitional clustering that vertices are joined into groups according to their common similarity [5].

A spectral clustering method for finding communities in social network is presented in [12]. In this method for completely use of network features, core members are used for mining communities, the authors utilized page rank method for community detection and proved that their method is better in terms of time and accuracy.

An accurate review of some community detection algorithms is proposed in [13] that gives the description about the algorithms and their results in detail.

One of the most popular algorithm is presented by Neman and Girvan (denoted GN) [6][14] which is a divisive hierarchical clustering algorithm. Edge removal divides network to communities, the edges to remove are chosen by using betweenness measure. The idea is that if two groups are linked by some edges between them, then all the paths between vertices in one group to vertices in other groups include these edges. Paths give scores to edges betweenness, by accounting all the paths passing through each edge and removing the edge with maximal score, links within network are broken. This process is repeated and is divided to smaller paths until a stop criterion is reached, this criterion is modularity. A hybrid model of this approach in [15] and a faster version based on same strategy in [16] is proposed.

Chen and Yuan have mentioned that counting all possible shortest paths in the calculation of the edge betweenness can make unbalanced partitions, with communities of very different size, and proposed to count only non-redundant paths, i. e. paths whose endpoints are all different from each other. The resulting betweenness shows better results than standard edge betweenness for mixed clusters on the benchmark graphs of Girvan and Newman. Holme et al. have used a modified version of the algorithm in which vertices, rather than edges, are removed. A centrality measure for the vertices, proportional to their site betweenness and inversely proportional to their in-degree is chosen to identify boundary vertices, which are then iteratively removed with all their edges. This modification which is applied to study the hierarchical organization of biochemical networks is motivated by the need to account for reaction kinetic information, that simple site betweenness does not include. Only the in-degree of a vertex is used because it indicates the number of substrates to a metabolic reaction involving that vertex [5].

Approaches to community detection based on genetic algorithm are available in [17][18][19]. In [4] genetic method is proposed that algorithm uses a fitness function which makes able to identify groups of vertices in the network that have dense intra connections and sparser inter connections.

In [20][21] authors proposed a genetic algorithm that uses Newman and Girvan fitness function for measuring network modularity. An individual is included of N genes that N is the nodes number. The ith gene corresponds to jth node, and it’s value is the identifier of node i. Authors use a non-standard one-way crossover in which, given two individuals A and B, a community identifier j is chosen randomly, and the identifier j of nodes j 1 ,…,j h of A is transferred to the same nodes of B.

A random graph is produced by some random processes and the features like number of nodes and edges and links between them are identified randomly. This method in [23] is used for community detection in networks.

In data mining, community detection is a clustering problem. Members between clusters can place in one or more clusters which is called community overlapping. Identifying of this overlapping is done in [24]. Authors proposed a new algorithm for identifying the community overlapping in complex networks using fuzzy c-means clustering approach. In figure 3 we can see an example of overlapping communities. The concept of modularity matrix for community detection is introduced in [25].

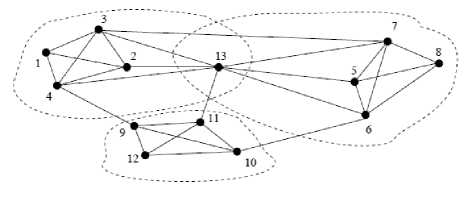
Fig. 3: An example of overlapping communities [26]

Random walks have important advantages such as they detect community structure, this approach is used in [8], it is based on short random walks and it is supposed that the “nodes that are visited during a same walk belong to a same community”. A part of proposed method in this paper is based on random walks.

Extremal Optimization (EO) method is proposed in [27] for finding communities which is a divisive algorithm for graph partitioning. In this method modularity is optimized by using a heuristic search based on EO algorithm. Authors produced results using real and simulated computer networks and compare with other approaches.

• III.    Proposed Method

• 3.1    Random Walk

The proposed approach is a combination of random walks and random local search agent which is applied in [28]. At first these approaches are discussed then theproposed method is represented.

Random walk is a process which can find communities in a network, in other words when a random walk is used, it scans the nodes in some steps; it begins with an initial node and based on a random process progresses to neighboring nodes.

In [8] the basic idea is performing short random walks and it is supposed that the nodes which are visited during the same walk belong to the same community. The next node that should be visited during a walk is one of the neighbors of visited node which is selected randomly.

At first an n×n similarity matrix S is defined to aggregate the walks which each entry S[i][j] shows the similarity of nodes i and j; all entries are initialized to zero. Every node in the network is then used as starting point for a random walk once. From that node some user-specified number of steps (num_steps) are taken through the network, selecting the next node probabilistically from all neighbors (a node may be visited any number of times during a walk). Nodes reached during such walk are recorded in set C as evidence of belonging to the same community. After each walk, entries in S corresponding to the nodes in C are incremented. The number of steps can either be determined based on some graph theoretic measure (e.g. diameter, number of nodes) or provided as input by the user. Once all walks are completed, each entry in the matrix denotes how often two nodes appeared along the same walk. A higher value indicates an increased likelihood of belonging to the same community.

Figure 4 shows the algorithm of the process which is mentioned above. This idea is used in this paper too but with some changes. In section 3.3 it is explained completely.

Input: numsteps, the length of the random walks

• 1:    for all nodes f- 1.....n, j = 1.....n do

• 2:    S[i][j] = O

• 3:    end for

• 4:    for each node start-node = 1,.... n do

• 5:    i = start-node

• 6:    C = {startjiode}

• 7:    for number of steps h = 1..... numsteps do

• 8:     randomly select next-node from neighbors(i)

• 9:     С = Си {next-node}

• 10:    i = next-node

• 11:    end for

• 12:    for each node i e C do

• 13:    for each node j eC, i ^ j do

• 14:        S[i][/]+ = 1 ‘

• 15:    end for

• 16:    end for

• 17:    end for

• 3.2    Random Local Search Agent

Fig. 4: Community detection with random walks algorithm [8]

In last decade different agent-based solutions were proposed to solve optimization problems. One of the successful approaches to agent-based optimization is the concept of A-Teams. An A-Team is composed of simple agents which represents complex collective behavior. The A-Team architecture first proposed by Talukdar [29] as a set of objects that include multiple agents and memories which through interactions, produce solutions for optimization problems. Random local search agent is used in [28] to solve distributed and non-distributed clustering problems. In fact to cope with these problems it is proposed to use a set of agents cooperating within the A-Team. A middleware environment developed by authors in [28] and referred to as JABAT (JADE-Based A-Team) is used to implement clustering problem.

As it is mentioned before, in fact communities in social networks are clusters. The global process of random local search agent is shown in figure 5.

Public class Random Local Search extends OptiAgent{

Public void improve Solution () {

CPSolution tempSolution= (CPSolution)

/* where solution is the solution that has been sent to optimize*/

Do {

Select randomly two different elements a and b from tempSolution. where a and b

Belong to different clusters;

Exchange values between a and b producing new Solution;

Calculate fitness of the new Solution;

If (new fitness value < old fitness value) TempSolution=new Solution;

} while (! terminating Condition);

/* solutionis ready to be sent back*/

Solution=tempSolution;

Fig. 5: Pseudo code of random local search agent [28]

• 3.3    Proposed Approach

Random walk approach in [8] is used in this paper for network partitioning and at end random local search agent is implemented to improve community structure quality and optimizes modularity factor. The proposed approach is as follow:

• •    At first all nodes in the network are considered as one community, then a node is selected randomly and put in a new community and its neighbors are calculated (neighbors of a node are nodes that in the graph of the network, there is an edge between them and that node).

• •    Then for number of steps, among the neighbors, a node is selected randomly and put in the new community (the number of steps can be determined based on some graph theoretic measures (e.g. diameter, number of nodes) or is got by user as an input [8]).

• •    Then the modularity Q of these communities is calculated.

• •    By using random local search agents, two nodes are selected randomly that belong to different communities and their community ID is exchanged. The process is repeated until maximum modularity Q is reached and then all links between both communities are removed.

• •    This process is done recursively with every resultant community until modularity could not be improved.

The empirical results on two social network datasets showed that the proposed method gives better modularity in comparison with other approaches.

• IV.    Evaluation

In this section the proposed approach that has been written in MATLAB is tested on two social network datasets, Zakhary Karate Club [30] and Jazz Musicians of Gleiser and Danon [31] and is compared with other algorithms. These networks are undirected and connected, so no transformation has been conducted.

• V.    Conclusion

• 4.1    Zakhary Karate Club Network

• 4.2    Jazz Musicians Network

  The network of collaborations between early jazz musicians of Gleiser and Danon [31] from The Red Hat Jazz Archive has 196 nodes and 2742 edges. A link between two nodes means that they have at least one musician in common. Table 2 compares the modularity results obtained by proposed algorithm and GN [14], Newman [15] and DA [27] that shows proposed algorithm gives better modularity. The results partition of proposed method on this network consisted of 5 communities.

In this paper an algorithm is proposed for clustering in social networks. Random walks are used to make communities and at last random local search agent is implemented to improve community structure quality. The empirical results on two social network datasets showed that the proposed method gives better modularity in comparison with other approaches.

This dataset describes the personal relations between members of a karate club and was created by Zachary [30], who studied the friendship of 34 members of a karate club over a period of two years and analyzed how the club is divided into two new clubs after an internal conflict. Zachary could show that the personal relations where a good indicator for the prediction of which member joined which of the new founded clubs. This dataset has been used by several authors to evaluate the quality of clustering methods. It has 34 nodes and 78 edges. In table 1 the results for the maximum modularity achieved by proposed algorithm is compared to the modularity obtained by GN [14], Newman [15] and DA [27] that shows proposed method gives better modularity. The results partition of proposed method consisted of 4 communities.

Table 1: Results of proposed method on karate network

Algorithm	Modularity
Newman	0.381
DA	0.419
GN	0.401
Proposed Method	0.426

Table 2: Results of proposed method on karate network

Algorithm	Modularity
Newman	0.438
DA	0.445
GN	0.405
Proposed Method	0.441