Социолого-математическая модель анализа региональной мифологии

Расширение информационного пространства в настоящее время привело к тому, что в больших количествах и с огромной быстротой продуцируются социальные, политические, художественные, религиозные мифы в виде факторов, влияющих на жизнь общества. Мифы, несмотря на свой иллюзорный характер, оказывают вполне реальное воздействие на социальное поведение.

Современная мифология может выступать в виде сложной мобилизующей структуры, способной вписывать индивидуума и массы в социальную реальность, создавая при этом у своих адептов впечатление истинности и состояние психологического комфорта. Информация, оформленная в оболочку мифологических представлений, приобретает чувственно-выразительную конкретность, легко запоминается и направляет социум в «объятия» иллюзий, делая его объектом различных манипуляций.

МОРОЗОВ Евгений Иванович, профессор кафедры социологии и политологии Ульяновского государственного университета, доктор социологических наук.

ГАЛКИНА Елена Петровна, ассистент кафедры социологии и политологии Ульяновского государственного университета.

Анализ места и роли мифологии в процессах формирования структуры властных отношений является одним из приоритетных направлений в исследовании и понимании ряда взаимосвязанных между собой социально-политических процессов, происходящих сегодня на федеральном и региональном уровнях.

В контексте заявленной проблематики представляется актуальным построение социолого-математических моделей анализа региональных мифологических конструктов как сложных систем в условиях неопределенности. Под сложной системой будем понимать такую, у которой при удалении некоторых компонентов могут быть утеряны принципиальные свойства, а при добавлении — возникать качественно новые свойства.

Предположим, что в ходе социологического опроса респонденту предложены характеристики, с помощью которых он может ассоциировать некий образ руководителя (например, губернатора). При этом они подобраны таким образом, что половина из них является характеристиками героя мифа, вторая — контрмифа1. При обработке анкет подсчитываются относительные частоты встречаемости каждой предложенной характеристики. Если все частоты одинаковы, то никакого противопоставления мифологических героев по отношению друг другу не существует, или вообще нет в данный момент никаких образов мифологических героев, или характеристики подобраны некорректно и все выглядят одинаково привлекательно для образа рассматриваемого лидера.

Когда в обществе существуют некоторые образы мифологических героев, то особенности мифологического сознания человека подсказывают, что отмеченные характеристики у каждого респондента будут поляризованы в соответствии с его предпочтениями. Разбиваем характеристики на две группы: первая — характеристики героя мифа, причем максимальное значение частоты для них должно приходиться на середину этой группы; вторая, со следующими номерами — характеристики героя контрмифа. Прочие характеристики мифологического героя располагаются симметрично относительно максимумов частот. Тогда они представляют собой гистограмму эмпирического распределения некоторой случайной величины, которую можно назвать «популярность мифологических героев в идеальном образе руководителя». Обозначим эту случайную величину G

Примеры сглаженных гистограмм такого типа имеют отчетливый вид бимодального распределения, где максимумы располагаются в точках с фиксированными абсциссами х = 0,25 их — 0,75. Это определяется особенностями построения гистограмм, отвечающих представлениям об управлении социальными системами в условиях неопределенности с помощью нечетких множеств. Задача состоит в том, чтобы дать теоретическое описание бимодальной переменной, выявить ее параметры и законы ее изменения.

Обращают на себя внимание три параметра таких распределений. Это величины двух максимумов в точках х = 0,25 и х = 0,75. Они характеризуют популярность героев мифа и контрмифа. Третий параметр введем как — площадь левой половины подграфика гистограммы. Этот параметр характеризует долю количества респондентов, готовых проголосовать за носителя черт героя мифа. Величина (l-/z) характеризует то же самое для героя контрмифа.

В связи с этим несомненный интерес представляет теоретико-вероятностная модель случайной величины G2 Возьмем за основу функцию плотности распределения усеченной нормальной случайной величины с параметрами а — математическое ожидание и а — среднее квадратическое отклонение. Тогда, если взять две такие функции Фх^ с а = 0,25 и фАх^ с а = 0,75 и составить из них линейную комбинацию где /ig[0;1], <7],<72 — параметры (<712>0), то получим основную для нас в дальнейшем функцию плотности распределения некоторой случайной величины X. При малых ovaI функция плотности обладает свойством бимодальности, причем ее максимумы близки к х = 0,25 и х = 0,75. Значения /(х) в точках максимума обратно пропорциональны соответствующим ох,а2.

Трудно переоценить значения адекватности результатов социологического опроса и его теоретико-вероятностной модели. Приведем обоснование того, что гистограмма, полученная по результатам социологического опроса, описанного выше, должна быть близка к теоретическому распределению (1) при некоторых значениях параметров ара2, м. Для этого сопоставим социологический опрос и статистическую процедуру моделирования. «Элементом» выборки здесь являются ответы респондента. Пусть было опрошено N респондентов. Среди них, предположим, п1 — сторонников героя мифа, n2 = N - п} — сторонников героя контрмифа. Предпочтения респондентов первой группы, по нашему построению, сгруппированы на гистограмме вокруг точки х = 0,25, что не мешает этому респонденту указывать отдельные характеристики, присущие герою контрмифа.

Внутри же «своей» группы предпочтений характеристики могут быть подобраны так, чтобы они имели причинную связь с главной (главными) характеристикой, и при этом связь убывала бы по мере удаления вдоль оси ОХ. В средней части гистограммы (х = 0,5) должны располагаться характеристики, имеющие отдаленную (относительно малую) причинную связь с каждой из главных характеристик.

Поскольку выбор той или иной характеристики в сознании человека обусловлен большим количеством различных причин, часто малозначимых по отдельности и независимых друг от друга, то становится правдоподобным, что наша гистограмма внутри каждой группы характеристик будет похожа на график плотности распределения случайной величины. Тем самым приходим к теоретическому распределению (1). При малом а_х почти вся «энергия» интереса к идеям героя мифа сконцентрирована в одной или двух характеристиках, по-видимому, ярких и привлекательных для его сторонников. При больших а_х интерес к идеям героя распределен по многим характеристикам его группы.

Значение Ц выражает долю сторонников идей героя мифа, (1-^и) — доля героя контрмифа. Если мы примем, что среди респондентов нет сторонников «третьей силы» или равнодушных людей, не способных сделать выбор между двумя героями, то ц есть рейтинг героя мифа или вероятность того, что случайно выбранный респондент отдаст свой голос именно за него. Величину М можно вычислить, используя свойства нормального распределения. Тогда она будет функцией, сложным и нелинейным способом зависящей от а, и а2. Для выражения этой зависимости построим номограмму линий уровня функции ^(а^^). На ней кривые, помеченные значением функции и, есть множество точек (а,,^), на которых величина и постоянна. Легко заметить, что все эти кривые располагаются симметрично относительно диагонали квадрата, на которой ах=а2, а значение ^ = 0,5.

Не менее важное значение имеют траектории социальных изменений. Номограмма зависимости ц^а^о^ является удобным инструментом для описания изменений значений бимодальной переменной G, а, следовательно, изменений состояния социальной системы властных отношений. Под значением бимодальной переменной будем понимать точку на номограмме с координатами (сГ],а₂) и значением рейтинга jiz.

Выделяются две зоны социальной устойчивости: левый верхний угол — для героя первого мифа, правый нижний — для второго. Нахождение точки в одной из этих зон означает безраздельное господство на социальной арене одного героя. По временному интервалу в таких зонах герой может находиться годами и даже десятилетиями. Однако общественное сознание, в том числе выраженное в мифологических образах, рано или поздно требует новых ярких личностей, идей, которые стараются привлечь сторонников.

Тогда с течением времени точка начинает «перемещаться» по номограмме. Если при этом «движение» направлено вдоль некоторой линии уровня к левому нижнему углу номограммы, то происходит обострение столкновения мифа и контрмифа героев, поляризация мнения общества о них. Если движение направлено к правому краю, то происходит диссипация (рассеивание) мифов.

Перемещение точки перпендикулярно линиям уровня означает быстрое изменение рейтингов героев, хотя величины а_г и сг₂ нашей бимодальной переменной при этом изменяются мало. Причинами перемещения могут быть появление «третьей силы», выброс компромата и т. п., или накопленная в ходе предыдущих шагов инерция.

Расположение точки вблизи диагонали номограммы (где а, = а2 ) следует признать неустойчивым положением рав- новесия, причем степень неустойчивости растет с приближением точки к левому нижнему углу. При этом любое внешнее воздействие, даже небольшое и случайное, приводит к существенному изменению ситуации. Здесь возможно два исхода: побеждающая сторона развивает успех, и через некоторое время точка попадает в зону устойчивости; проигрывающая сторона отбивает атаку и возвращается в прежнее состояние. Например, к середине 1999 г. в Ульяновской области сложилась стабильная социально-политическая ситуация. Областью более десяти лет руководил Ю. Ф. Горячев, который за эти годы приобрел образ героя, характеризующегося как «хозяйственник», «защитник простого народа» и т. п. Достойных противников у него не было (ситуация А) (рисунок). Однако уже летом 1999 г. появился новый мифологический герой (генерал В. А. Шаманов) с характеристиками «защитник отечества», «воитель», «воплощение дисциплины и порядка» и т. п. В течение двух месяцев (сентябрь-октябрь) он приобретал популярность в обществе (траектория от А до В). При полном бездействии команды Ю. Ф. Горячева произошла недооценка притягательности нового мифологического образа, обладающего яркими характеристиками, которые резко отличались от присущих Ю. Ф. Горячеву.

В ноябре-декабре 1999 г. изменилась траектория (от В до С), то есть ситуация быстро перешла зону неустойчивости и, не встречая организованного сопротивления противника, достигла точки С в день выборов (21 декабря 1999 г.).

На пике успеха произошло дальнейшее движение перпендикулярно линиям уровня и в 2003 г. достигло точки D нашей номограммы. Однако до зоны стабильности (Е) новый миф не дошел. Яркие характеристики тускнели, команда не оправдала надежд избирателей. Произошла диссипация мифа, то есть рассредоточение тех, кто разделял данный миф, а также снижение концентрации тех, кто продолжал его поддерживать, прослеживалась поляризация мифа и контрмифа в малом количестве тех, кто готов поддерживать контрмиф.

Далее траектория движется к точке К. В этот момент возникает другой миф, который, используя положительные характеристики Ю. Ф. Горячева и апеллируя к ностальгическим чувствам населения, побеждает на новых выборах.

Об анализе региональной мифологии

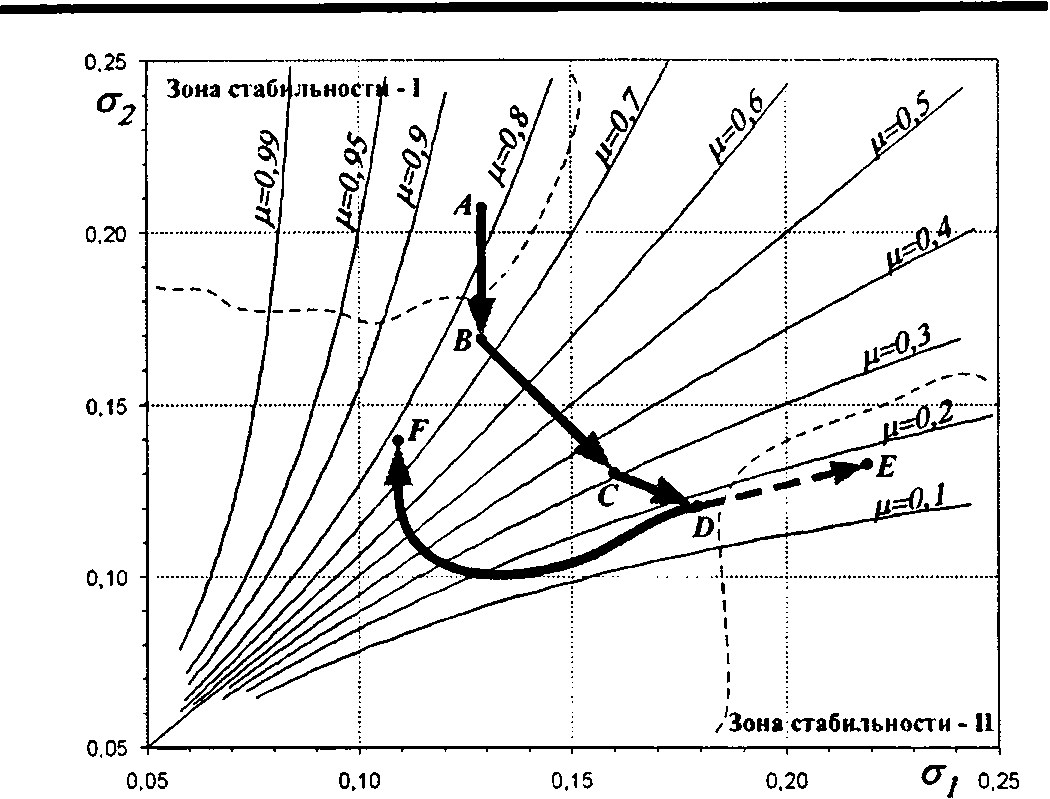
Рис. Траектория динамики региональных мифа и контрмифа

Таким образом, предложенная математическая модель позволяет анализировать сложную социальную систему, действующую в условиях неопределенности, трансформацию мифа, выявлять контрмиф, когда еще ничего не указывает на какие-то проблемы с рейтингом, а также обнаруживать те моменты времени, когда возможно максимально воздействовать на рейтинг мифологического образа.