Содержание и сущность права граждан на неприкосновенность частной жизни, личную и семейную тайну

Выше предела расхода p Электропроводность композита, состоящего из смеси гетерогенного материала изолятора и проводника. σ концентрация проводящей фазы p уровень связан:

(3.1)

Здесь критический индекс t зависит от размера системы:

t = 1,2 ± 0,1     в двух измерениях t = 1,7 ± 0,1   к трем измерениям

Существует некоторое обобщение этой проблемы, которое позволяет ввести в систему анизотропию, что приводит к оценке проницаемости через тензорную величину.

• 1)    Проводящая фаза может состоять из направленных частиц (волокон, цилиндров), и проводимость такого материала всегда

изотропна.

• 2)    Проводящая фаза состоит из частиц, ориентированных с анизотропной удельной анизотропной удельной проводимостью.

Этот вопрос был детально изучен Шкловским и показал, что такой материал всегда анизотропен. Только в области, близкой к очень малой границе потока, это не выполняется, и в ней анизотропия уменьшается вблизи границы по закону Шкловского.

— = 1 + (Р - Pc ) ' , °1

(3,2)

Здесь l - новый критический индекс.

Проблема анизотропии может быть рассмотрена с помощью сеточной модели в контексте проблемы садов.

• 3)    Связи в разных направлениях будут производить новую ионизацию с разной вероятностью, но будут иметь одинаковое сопротивление. В этом случае проницаемость анизотропна в поле вблизи предела тока.

• 4)    Все связи образуются с одинаковой вероятностью, но

сопротивление меняется в разных направлениях.

В этом случае проводимость также вся, кроме изотропной сферы, близкой к пределу потока. p анизотропный. Модель сопротивления решетки также рассматривается с точки зрения ренормационной группы, результаты близки к результатам, полученным при численном моделировании с использованием эффективной среды.

Электрические свойства композиционных материалов с анизотропными сферами или изотропными вытянутыми частицами подробно исследованы Шкловским. Оба случая были эквивалентны в изменении координат, в результате чего сфера была переведена в эллипсоид, оставаясь того же размера.

Агар с и s макроскопическая проницаемость системы эллипсоидов по осям z и x ориентирована также по оси z ст' и с[ Z- Если осевая и поперечная анизотропные сферы имеют макроскопическую проницаемость, они будут связаны следующим соотношением.

^с 11 =

(l у3 I d)

с '| , ^с 1

d с 1

а ¹ >       (3.3)

Вот ^l Отношение больших и малых концов эллипсоида. d

Систему анизотропных сфер можно смоделировать как анизотропные сады.

Изменение критического значения коэффициента анизотропии для ориентированных в нем изотропных эллипсоидов:

с ^с 1

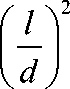
1 + A ( Р - P c ) A

(3,4)

Это будет на вид. Тот факт, что критический индекс l составляет около ~ 0,4, был определен численными расчетами с использованием метода ренормагу-группы и моделирования с использованием дерева Кейли (решетчатые сады и

(l у2

метод квадруполей). Анизотропный размер ~ равно

Объемная концентрация макроскопической проницаемости и коэффициента анизотропии p Общий случай конечной проницаемости матрицы в функции n описан на следующем рисунке (см для анизотропной матрицы: 7П1 и 7^)

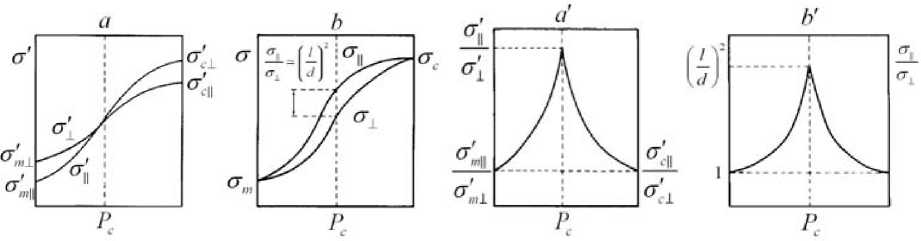
Рис 1. Электропроводность (a, b) композитного материала, а также анизотропная и электропроводность ( a , b ) Насыпная концентрация наполнителя дана на общем виде связки. ( a 5 a ) - анизотропные сферы в анизотропной матрице, ( b ⁵ b ) - изотропные частицы, растянутые в матрице с изотропной конечной проницаемостью.

При численном моделировании и анализе экспериментальных результатов необходимо учитывать конечные размеры системы, так как они имеют большие статические колебания проницаемости, которые возрастают при приближении к пределу потока и затрудняют интерпретацию результатов.

По словам Стрейли

{ 5(7 '?  %

77  L

(3.5)

Вот % - длина когерентности, %~ (p-pc) v , n = 1,35, размер системы L, т.е. чем меньше размер системы и чем ближе к пределу расхода, флуктуация фактически увеличивается.