Согласование интересов в условиях определенности посредством кластеризации социально-экономических позиций

DOI:

В современном мире одним из серьезных противоречий является несогласованность между растущими потребностями и ограниченными ресурсами. Поэтому в экономической теории важнейшим и неизменным вопросом является поиск возможностей для устойчивого развития (точнее, для поддерживаемого развития – от англ. sustainable development ) при взаимодействии различных субъектов социально-экономической системы.

Для достижения такого развития требуется согласование интересов субъектов системы, которое возможно осуществлять, несомненно, разными путями, но на основе наличия хотя бы частичной общности целей, средств их достижения, мотивов, образа мышления, поведения и прочего. Согласование интересов не устраняет противоречий (особенно в динамично меняющемся мире), но позволяет сглаживать их, формируя окружающую среду как более прогнозируемую и сбалансированную, уменьшая шансы на возникновение социальных потрясений.

В качестве одного из возможных примеров взаимодействия заинтересованных сторон, каждая из которых имеет собственные представления о требуемых для своей деятельности величинах или долях ограниченных ресурсов, требующих распределения, можно указать на связанные с некоторой фирмой (компанией) субъекты и их цели. Так, рабочих и специалистов фирмы интересует ресурс заработной платы, ресурс карьерного роста, ресурс самостоятельности и прочее. Аналогичная система интересов наблюдается у менеджмента фирмы (но при этом с иными значениями запросов в отношении соответствующих ресурсов). Однако у менеджмента, поми- мо уже указанных интересов, имеются и другие, например связанные с необходимостью развития фирмы, увеличения ее капитализации. Иными словами, у различных субъектов социально-экономической системы могут быть частично пересекающиеся наборы интересов и, в их рамках, разная степень заинтересованности в имеющихся ресурсах. Формально можно сказать, что набор интересов у всех один и тот же, но у каких-то из сторон степень заинтересованности в некоторых ресурсах может не сильно отличаться от нуля. В этих условиях нужна оптимизация ресурсного обмена, без которой достижение целей заинтересованных сторон без попытки достичь какого-либо компромисса может быть возможна разве что при чьем-либо увольнении.

Другой пример – это случай объединения на различных основах стран в целях укрепления данного сообщества и повышения экономического роста государств, составляющих содружество, типа ООН, G20, G8, СНГ, ЕС, БРИКС, АТЭС, АСЕАН и прочих. У стран содружества при этом имеются собственные интересы, которыми они не могут поступиться в полной мере при дележе тех или иных ресурсов, скажем, при выбросах в атмосферу парниковых газов, при промышленном рыболовстве в океанах. Однако согласование и учет взглядов друг друга все же необходимы в целях добрососедства, для защиты экологии, для недопущения прогнозируемой катастрофической деградации рыбных запасов и т. д.

Поиск ответа на вопрос, как лучше всего сблизить позиции в ситуациях, подобных перечисленным и практически всегда многокритериальных, – нетривиален. Настоящая работа может помочь в выявлении путей и механизмов решения описанной проблемы посредством предложения определяемого автором компромисса в виде установления дополнительных взаимосвязей между элементами социально-экономического пространства.

Основные положения.Математическая модель задачи

Рассмотрим подробнее следующую ситуацию, в которой предлагается подход к анализу возможности согласования интересов.

Введем следующие обозначения. Пусть U ₁, ..., U_n – индивиды, составляющие рассматриваемое общество, для которого выделен общий список признаков F = { F ₁, …, F_m }, характерных для каждого из U_i .

Пусть f j е R¹ - желаемое для U i значение признака с именем F j , а А _у - величина возможного, по мнению U_i , отклонения значения этого признака в ту или иную сторону (что, для определенности, назовем «степенью толерантности»).

Таким образом, каждый индивид U_i определяется m -мерным бивектором:

U ~ ( f 1 , А_ч), ..., (f ^ , A _m )), или, иначе, его образ представляется в виде декартового произведения D_i :

U i ~ D i = [f i i — A i , f 1 + AJ x ... x

^{X f} im ^im , ^f m "*"A m ^] "

То или иное пересечение P некоторых множеств D_i естественно рассматривать как некоторую «базу согласия» или некоторую основу, на которой возможно согласование интересов индивидов, соответствующих этим множествам.

То есть установление в обществе состояния, описываемого любой m -мерной точкой из указанного пересечения, означает отсутствие конфликта между соответствующими индивидами.

Например, если пересечение всех D_i не пусто, то конфликт в обществе отсутствует и для поддержания данной ситуации требуется общественный выбор любой из точек такого пересечения. А если никакая пара множеств

D_i не пересекается, то общество максимально конфликтно.

В общем случае следует выяснить, к какому из имеющихся непустых пересечений множеств D_i будет, в некотором смысле, оптимальным отнести каждого индивида в целях снижения общей конфликтности общества.

Будем рассматривать «базы согласия» коалиций индивидов U_i , обозначив их через P^r (см. рис. 1):

Pn = D n^nD -11

пересечение всех n множеств D_i ,

Pn-1 = D П^П D    (q = 1,^, Cn-1)- qq         q пересечение тех или иных n–1 множеств из всех имеющихся Di,

Pn-2 = D n^n D    (q = 1,^, Cn-2)- qq         qn пересечение тех или иных n–2 множеств из всех имеющихся Di и т. д., до

Pq2 = D nD (q = 1,^, C2)-qqqn пересечение тех или иных пар множеств из всех имеющихся Di.

Всего этих множеств-пересечений:

Cn + Cn-1 + Cn-2 + ^ + Cn = 2n - n-1, и тогда их полный или даже разумный перебор методом ветвей и границ для поиска указанного выше решения представляет собой в смысле теории алгоритмов труднорешаемую

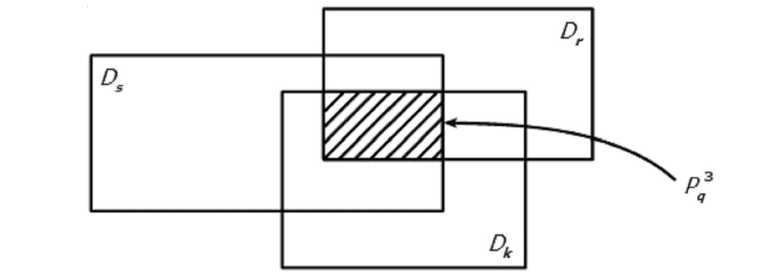
Рис. 1. Пример базы согласия

Примечание . Составлено автором.

задачу [1], в силу чего здесь следует применять непереборные алгоритмы.

Присвоим введенным базам согласия ранги: rgP q = r (то есть наивысший по значимости ранг, равный n , присваивается множеству P ₁ ⁿ , а наименьшие ранги, равные по 2, присваиваются множествам P _q ² ).

В случае, когда планируется отнести или приписать индивида U_i к базе согласия P_q^r , будем оценивать возникающую степень терпимости этого индивида, с очевидным предположением о том, что с чем большим рангом базе согласия будет приписан индивид, тем большая ему будет присуща степень терпимости к ситуации, возникающей по отношению к нему.

В связи с этим сформируем матрицу таких значений.

Пусть

A = A         = n х (2 n - n -1)

= [ A (U ., P r )]. .

• ^{L v} i q^,Ai = 1, . , n

r = n ,...,2; q = 1,..., Cr n есть матрица степеней терпимости, которые проявляются при установлении взаимосвязи индивида Ui с базой согласия Pqr. Для наглядности укажем ее вид (см. таблицу).

Элементы матрицы A определим следующим образом.

Предположим, P q = 0 .

Тогда для каждого U_i полагаем A (U i , P^r ) = 0, то есть пустой базе согласия, конечн ^q о, нельзя приписать никакого индивида и нельзя при помощи нее увеличить сколь бы то ни было степень терпимости в обществе.

Предположим теперь, что P q * 0 .

Тогда для каждого U_i , такого, что

• D. П P^r * 0 , полагаем

iq

A U- Pr ) = r, q то есть степень терпимости считаем равной рангу непустой базы согласия, с которой у образа Di индивида Ui имеются точки пересечения (напомним, что получение такой величины степени терпимости возможно лишь если индивид Ui будет отнесен к данной базе согласия, а не к какой-то другой – см. рис. 2).

Здесь стрелками показаны возможные приписывания U_i к той или иной базе согласия, в том числе к не пересекающейся с D_i .

Наконец, предположим P q *0 .

Тогда для каждого U_i , такого, что

D i n P r =0 , полагаем A ( U i , P^r ) равным соответствующему значению, ^q получаемому при линейном отображении отрезка [minρ( D _i , P _t ^r ), maxρ( D _i , P _t ^r )] на отрезок [ r –1, t * i t

• r ]. А именно в указанном случае:

  A U , P r ) =

  q

  
  

p⁽ D , P r ) - ^minp⁽ D , P ^r )

I i ^q t * i it J ₊ max p( D. , P t^r ) - min p( D. , P t^r ) I . t ¹ t * i ¹ J

+ (r — 1), гдеρ(Di, Ptr) – некоторая заранее выбранная функция расстояния между множествами (причем P[ * 0). Например, для определенности, пусть r -минимум L1-метрики или, иными словами, минимум так называемого «манхэттенского расстояния», введенного Германом Минковским:

Таблица

Матрица степеней терпимости

A	n P 1	р n -1      ... P 1		P n -1 О 1 - 1 n	pn -2 P 1	^    E> n -2 C n - 2 n		…	P 1 2    …		2 PC 2 n
U 1
U 2
U n

Примечание . Составлено автором.

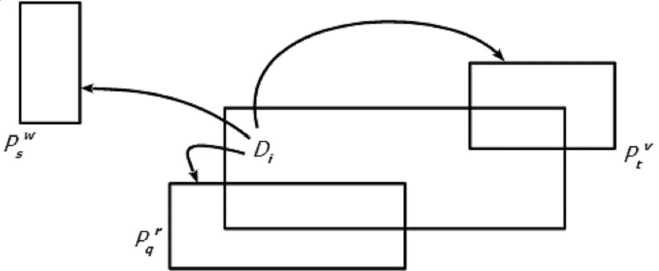
Рис. 2. Примеры возможных отнесений индивида к базам согласия

Примечание . Составлено автором.

p( A, B ) =      min      Z a s - b s l-

( a ) e A , ( b ) e B ss

Для большей наглядности продемонстрируем на рисунке 3, расстояния между точками какого типа придется подсчитывать.

Наконец, введем матрицу X планируемых приписываний индивидов U_i к тем или иным базам согласия P q ^r .

Пусть

X = X       = n x (2 n - n -1)

= [ X (U ., P r )]. .

i q i = 1,., n r = n,^,2; q = 1,...,Cr, n где X(U., Pr) = {0,1} и X(U., Pr) = 1 указывает на плiанqируемое устанiовлqение взаимо- связи индивида Ui с базой согласия Pqr, а X(Ui, Pr) = 0 указывает на отсутствие таких плаqнов.

Реализация же указанных планов будет осуществляться лишь после получения решения, оптимального в предложенном ниже смысле.

В результате имеем решаемую известными методами задачу целочисленного (псевдобулевого) программирования [7; 15; 16; 18], в целевой функции которой можно, при необходимости, учесть веса wt ( r ) баз согласия, например, в соответствии с эмпирическим психофизиологическим законом Вебера – Фехнера (заключающимся в том, что интенсивность ощущения пропорциональна логарифму интенсивности раздражителя), или в соответствии с модификацией Стивенса этого закона и т. д. [10; 12]:

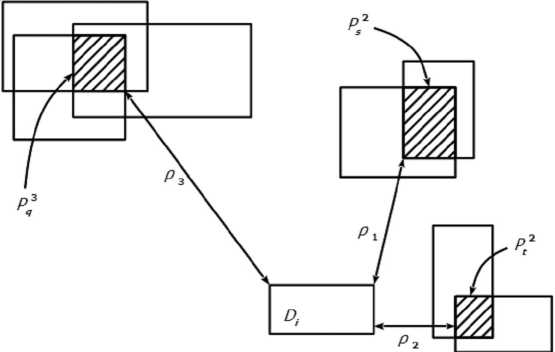
Рис. 3. Примеры случаев подсчета расстояний между множеством образа индивида и базами согласия

Примечание . Составлено автором.

'         Z        [ wt (r) A (U., p;) • X (U., p;)] ^ max i = 1,..., n                                  i q 1 q

• r = n ,...,2; q = 1,..., C r

n

Z         X (U ., P r ) = 1( i = 1, ^ , n )

• I                                           r ¹ q                                                           ,

r = n , ^ ,2; q = 1, ^ , C r n

Z X(UP ^r ) >  0( r = n, ^ ,1; q = 1, _ , С Г ) iq                n

• 1    = 1, ^ , n

^ X(U_i , P q^r ) = {0,1}( i = 1, ^ , n ; r = n , ^ ,2; q = 1, ^ , C r )

где каждое ограничение-равенство трактуется как замечание, что всякий индивид должен быть отнесен только к какой-то одной базе согласия, а каждое ограничение-неравенство трактуется как замечание, что ко всякой базе согласия может быть отнесено 0, 1, 2, …, n тех или иных индивидов.

Заметим, что в описанном смысле оптимальное решение полученной задачи существует в силу конечного количества допустимых решений.

Предложенные в работе рассуждения очевидно указывают на пути дальнейших обобщений в рамках предложенной тематики. Для этих исследований следует привлекать различные математико-статистические методы с целью повышения адекватности строящейся модели реальности.

Заключение

Необходимо отметить, что получаемое в результате оптимальное решение модели не следует рассматривать как основание для насилия над субъектами в целях «принуждения их к миру». Насилие порождает ответное насилие и возникновение новых плохо предсказуемых издержек, а значит, и возникновение новой социально-экономической ситуации, для которой потребуется создание своей собственной, более сложной, модели.

Оптимальное решение модели имеет смысл воспринимать как часть переговорного процесса по сближению позиций при формировании «общественного договора», как обоснованное предложение для обсуждения субъектам изучаемой системы способа достижения компромисса, в то время как абсолютное согласие экономических интересов индивидов, коллективов и общества в целом возможно лишь в идеале.

В связи с этим Дж.М. Бьюкенен в своей нобелевской лекции «Конституция экономической политики» говорил: «Общественный договор в философском смысле означает согласие, проистекающее из взаимодействия самих индивидов, а не всеобщее одобрение некоего абстрактного идеала» [5]. При этом очевидно, что если имеется такая сторона конфликта, которая не желает идти ни на какие уступки, то компромисс невозможен, какие бы подходы к его достижению ни предлагались.