Сохранение видов и условия эволюции

В природе происходят два противоположно направленных временных процесса: сохранение видов и эволюционные изменения в этих видах.

Впервые теория эволюции была разработана Ч. Дарвином. Движущими силами эволюции он считал наследственную изменчивость и естественный отбор. Он также показал, что различные породы домашних животных и культурных растений созданы человеком в процессе искусственного отбора. Однако теория Ч. Дарвина оставила без ответа вопрос о сущности и механизмах наследственной изменчивости. Непонятно, почему естественный отбор за миллионы лет не поднял все низкоорганизованные виды на высшую ступень организации. Например, почему у крупных животных до сих пор отсутствует разум на уровне человеческого? Эволюционирует ли мозг человека в направлении увеличения его умственных способностей?

В начале 20-го века появилась мутационная теория эволюции. Эта теория утверждает, что мутационные формы возникают внезапно и вполне устойчивы, в результате чего возникают новые виды. Однако из этой теории непонятно, при каких условиях устойчивы мутационные формы? В больших популяциях, например, в человеческой, непрерывно возникает большое количество различных мутаций у отдельных особей, которые зачастую полезны. Почему в целом человечество не умнеет, люди не становят- ся более подвижными, объем памяти не увеличивается и т. д.? Почему иммунная система до сих пор не победила рак? В целом человеческий вид сохраняется неизменным в течение тысячелетий. Непонятно, почему эволюция происходит столь медленно? Почему вид столь устойчив?

В настоящее время придерживаются синтетической теории эволюции, которая включает в себя, как элементы дарвиновской так и мутационной теорий эволюции.

Целью данной статьи является попытка ответить на некоторые из поставленных вопросов.

1. Сохранение видов и закон Харди – Вайнберга

Для того, чтобы понять, почему и каким образом происходят эволюционные изменения, рассмотрим законы сохранения вида.

Сохранение вида определяется законом Харди – Вайнберга [1].

Закон Харди – Вайнберга гласит, что в панмиктической (идеальной) популяции частота аллелей из поколения в поколение сохраняется неизменной. Полная панмиксия характерна для бесконечно больших популяций, где нет отбора, давления мутаций, миграций и т. д. В математической форме закон Харди – Вайнберга в простейшем случае двух аллелей гена устанавливает, что относительные частоты генотипов в поколениях соответствуют членам биномиального разложения ( p + q ) 2 так что p + q = 1, где p и q частоты аллелей в популяции.

Согласно этому закону генотипы АА , Аа , и аа при аутосомном наследовании имеют следующие частотные соотношения:

( AA ) p ² : ( Aa ) 2 pq : ( aa ) q ² . (1)

Равновесие Харди – Вайнберга безразличное. Для аутосомного наследования это очевидно. Действительно, используя распределение генотипов (1) можно получить, например, частоту рецессивного аллеля а в следующем ( n + 1 ) -м поколении. Для этого нужно сложить половину частоты гетерозигот Аа с частотой гомозигот аа :

q n + 1 2 ² p n q n ⁺ q n q n ⁽ p n ⁺ q n ) q n .

В следующем поколении получена такая частота аллеля а , что и в предыдущем.

же

Для генома, сцепленного с полом, требуется более сложный анализ.

Предположим, что аллели А и а сцеплены с Х -хромосомой. Частота аллеля А у мужчин p_m и у женщин p_f . Для аллеля а соответственно q_m и q f .

При скрещивании в первом поколении возникает соотношение генотипов у женщин в соответствии с произведением ( p f + q f ) ( p m + q_m ) :

( AA ) p f p m : ( Aa ) ⁽ p m q f + p f q m ): ( aa ) q m q f . ⁽³⁾

Используя распределение генотипов (3), можно найти частоту аллеля а у женщин в следующем ( n + 1 ) -м поколении:

^qf ( n + 1 )    2 ⁽ p mn q fn ⁺ p fn q mn ) ⁺ q mn q fn

= 2 ^^{( 1 —} q mn ) q fn ^{+ ( 1 —} q fn ) q mn J ⁺ q mn q fn = ⁽⁴⁾

= 2 [ q fn ⁺ q mn J .

При выводе (4) использованы следующие очевидные соотношения p_mn = 1 - q_mn и p f _n = 1 - q f _n .

Таким образом, частота аллеля а у женщин в следующем поколении равна полусумме частот аллеля а у женщин и мужчин предыдущего поколения, между которыми произошел репродуктивный контакт.

Для анализа эволюционных процессов важно отметить, что инбридинг (кровнородственные скрещивания) не нарушает сохранение вида. Обычно кровнородственными считают только связи до третьего поколения включительно [1]. Инбредные процессы характерны для родословной, поэтому далее мы будем анализировать родословную. Популяция обычно состоит из множества родословных.

В законе Харди – Вайнберга (1) инбридинг учитывается с помощью коэффициента инбридинга родословной F [1; 2]:

( AA ) ( p n + Fp n q n ): ( Aa ) [2 p n q n (1 — F )]:

: ( aa ) ( q n + Fp n q n ) .

Соотношение (5) для аутосомного наследова- ния было установлено английским генетиком

Райтом [3; 4] и носит его имя.

Соотношение Райта показывает, что в аутосомах потомства инбредной родословной при скрещивании наблюдается одинаковое увеличение частоты доминантных АА и рецессивных аа гомозигот. В тоже время уменьшается частота гетерозигот в 1 - F раз.

Вывод соотношения (5) можно найти, например, в книге [5].

В следующем поколении равновесие Харди – Вайнберга (5) по аутосомному геному в инбред- ной родословной восстанавливается:

q n + 1    2 ² p n q n ^{( 1} F ) ⁺ ( q n ⁺ Fp n q n ) q n .     ⁽⁶⁾

Для генов, сцепленных с полом, распределение аллелей имеет более сложный вид:

( AA ) p fn p mn ^{+ (} p mn q fn ^{+ p}fn^qmn ) 2 I ^:

^{: ( Aa} ) ^[( p mn q fn ^{+ p}fn^qmn )(1 — F )]:

F

: ⁽ aa ) q mn q fn ⁺ p mn q fn ⁺ p fn q mn ) 2 Г

Подробный вывод соотношения (7) можно найти, например, в статье [6].

В следующем поколении инбредной родословной частота рецессивного аллеля а у женщин равна полусумме частот аллелей а женской и мужской особи:

q f ( n + 1 )    2 ⁽ p mn q fn ⁺ p fn q mn ) ^{( 1} F ) ⁺

F

⁺ q mn q fn ^{+ (} p mn q fn ⁺ p fn q mn ) 2

= 2 ^^{( 1 —} q mn ) q fn ⁺ ( 1 ^— q fn ) q mn J ^{( 1 —}

⁺ q mn q fn = 2 ^[ q fn ⁺ q mn J ^.

F + F ) +

Проведенный анализ показывает, что инбридинг не выводит родословную из данного вида.

В реальности, полная панмиксия невозможна. Возникает вопрос, будет ли наблюдаться генная модификация в популяции при небольшом отклонении от панмиксии, и что будет происходить с данной модификацией в дальнейшем?

Популяция обычно состоит из множества родословных. Если для родословной закон Харди – Вайнберга записывается в рамках дискретной математики, то для популяции в целом справедлива запись этого закона в виде дифференциального уравнения [7; 8]. В популяции людей в каждый момент времени рождается множество потомков, поэтому процессы изменения числа людей (и, следовательно, распределения их генома) протекают фактически непрерывно и можно использовать методы функционального анализа.

Будем считать исследуемую популяцию некоторой системой, на которую осуществляется небольшое мутационное воздействие (негативный экологический фактор, радиоактивное излучение и т. п.). Полагаем воздействие относительно небольшим, поэтому взаимодействие системы и воздействия носит линейный характер.

3.    Мутационное воздействие на популяцию qf = const, что отражает неизменность частоты аллеля в соответствии с законом Харди – Вайнберга.

Рассмотрим решение уравнения (9) в виде:

q f ( n ) = q f о + J G ( n , n / ) D ( n / ) dn / ,            (10)

где q_{f 0} – начальная (до начала воздействия на популяцию) частота рецессивного аллеля у женщины; G ( n , n ^/) – функция Грина для популяции; n ^/ – параметр интегрирования – время воздействия, отклик на которое исследуется во время n , так что n >  n / .

Подставим формулу (10) в уравнение (9):

d ² ( q f о + J G ( n , n / ) D ( n / ) dn / )

dn ²

+

d ( q f о + J G ( n , n / ) D ( n / ) dn / )

= D ( n ) .

dn

Примем следующие начальные условия, отражающие тот факт, что начальная частота рецессивного аллеля не зависит от времени:

Характеристикой отклика системы на некоторое воздействие в общем случае является функция Грина этой системы [9]. Поэтому, прежде всего, найдем функцию Грина для слабо непанмиктической популяции.

На популяцию может действовать как детерминированный фактор, вызывающий генную модификацию, например, непрерывное радиоактивное излучение [10], так и случайные факторы, например, различные факторы канцерогенеза. Все эти факторы изменяют частоту аллелей в популяции, т. е. вызывают генную модификацию.

Рассмотрим дифференциальное уравнение, отражающее закон Харди – Вайнберга для аллеля сцепленного с полом, для популяции [7; 8], на которую действует некоторый мутационный фактор:

^{d 2} q f о = dq f 0

dn ² dn

= 0.

В этом случае уравнение (11) преобразуется к виду:

J

f- Gn _v    dn ²

dG ( n , n / ) + ln2--^--- dn

= J 5 ( n - n / ) D ( n / ) dn / .

В (13) воспользовались

5 -функции Дирака:

D ( n / ) dn / =

известным свойством

D ( n ) = J 5 ( n - n / ) D ( n / ) dn / .                (14)

Таким образом, из уравнения (13) находим уравнение для функции Грина популяции:

d ² G ( n , n ^/)        dG ( n , n ^/ )

---^—- + ln2          =5 ( n - n / ) .      (15)

dn ²            d ⁿ

d^- + ln2 d f = D(n , dn ²         dn ⁽ ) ’

где qf – частота рецессивного аллеля у жен-t щины; n =   — безразмерное время1 t — время;

Т – среднее время смены поколений (у человека примерно 25 лет); D ( n ) - функция времени, характеризующая воздействие на популяцию мутационного фактора.

Для панмиктической популяции D ( n ) = 0.

В этом случае решением уравнения (9) является

Полученное линейное дифференциальное урав-

нение второго порядка легко решается введени-

ем новой переменной Z ( n , n / ) =

dG ( n , n ^/ ) dn

.

Отметим, что функция Грина популяции не зависит от вида воздействия: детерминированное или случайное. Функция Грина популяции – это характеристика популяции, а не воздей-

ствия на нее.

Далее, полагая Z = uv, находим v = e ^{n ln2}. Для функции u дифференциальное уравнение имеет вид:

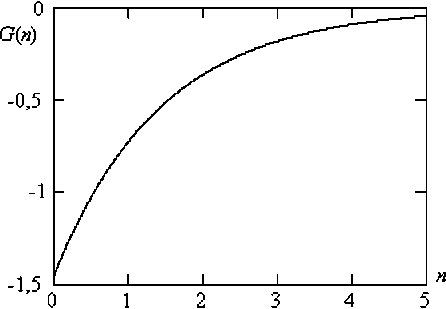
Рис. Функция Грина для двухаллельной генной системы, сцепленной с полом

du          / n ln2

— = 5 n - n e , dn                    , решением которого является:

u = J 5 ( n - n / ) e n ln ² dn =

• = J s ( n / - n ) e n ^ln2 dn = e n / ^ln2.

  
  
  
  

При нахождении (17) воспользовались четностью 5 -функции и свойством (14). Следователь-

- ( n - n / ) ln2

но, Z = uv = e v '   . Функция Грина популя- ции находится из условия:

G ( n , n / ) = J Z ( n , n / ) dn =

= J e - n

- n / ) ln2           1 - ( n - n / ) ln2

’ dn =-- e

.

ln2

Функцию Грина популяции можно представить в виде:

G ( A n ) = - —¹---,                         (19)

2 ^{A n} ln2

где A n = n - n / промежуток времени, прошедший от момента воздействия или точнее от момента окончания воздействия.

Знак минус указывает на то, что популяция всегда сопротивляется внешнему воздействию.

На рисунке показан график изменения функции Грина популяции, подчиняющейся закону Харди – Вайнберга в случае простейшей двухаллельной системы, сцепленной с полом. Минимальное значение функции Грина при A n = 0 равна G ( A n ) =- 1.443. При A n ^м функция Грина стремиться к нулю. То есть отклик популяции на воздействие приводит к постепенному нивелированию результата воздействия. Фактически, уже в 4–5 поколении геном популяции возвращается к исходному уровню, который существовал до воздействия. Этот факт хорошо известен селекционерам. Культурные растения, предоставленные сами себе, быстро дичают.

3.    Эволюционный процесс

Используя проведенный анализ, рассмотрим вопрос, каким образом может происходить эволюция популяции, т. е. наблюдаться изменение вида. Эволюция возможна только путем нарушения закона Харди – Вайнберга.

Для изменения вида необходимы два условия.

Первое условие: мутационное воздействие должно породить, по крайней мере, две особи, мужскую и женскую, которые относятся к другому, но одному и тому же виду. У разных матерей даже одной родословной это практически невозможно, т. к. мутации обычно происходят случайно и в разных локусах генома. Однако мать может родить две разнополые особи, у которых мутация одного и того же гена в Х-хромосомах произошла одинаковым образом. Естественно мутация должна быть рациональна и полезна для жизнедеятельности организма.

Второе условие: мутации генома родившихся разнополых особей не должны позволять этим особям вступать в успешный репродуктивный контакт с остальными особями родословной и тем более популяции. Либо результатом этого контакта должно быть потомство не способное к дальнейшему размножению. Естественно, репродуктивный контакт между мутантными особями должен быть обязательным и успешным. При этом возникшее потомство должно быть более конкурентоспособным по сравнению с остальными особями популяции.

Выполнение сразу двух условий исключительно редкий случай, поэтому эволюционный процесс очень медленный.

Если мутантная особь при скрещивании с не мутантной дает потомство способное к дальнейшей репродукции, то новый вид не возникнет и через 4–5 поколений результат мутации исчезнет. Этот процесс в популяции происходит очень часто и не ведет к возникновению нового вида. В этом суть закона сохранения вида.

Таким образом, новый вид возникает скачком в недрах прежней родословной и его основателями служат всего две разнополые особи. Это не противоречит теории существования единой праматери всего человечества.

Дальнейшее развитие нового вида вначале осуществляется инбредным образом в соответствии с распределением генотипов (5) и (7), что, как было показано ранее, не выводит особи за рамки этого вида.

Заключение

Мутационные изменения в популяции обычно исчезают в течение 4–5 поколений после возникновения мутаций и популяция возвращается в исходное по распределению генотипов состояние.

Вся популяция или ее часть одновременно эволюционировать не может, т. к. действ у ет закон сохранения вида.

Эволюционный процесс происходит за счет мутации точечно в потомстве одной женской особи, одновременно у мужского и женского потомка.

Эволюционный процесс может дать новый вид только при невозможности репродуктивного скрещивания нового и старого видов или если это скрещивание дает потомство не способное к дальнейшей репродукции.