Solution of irregular systems of partial differential equations using skeleton decomposition of linear operators

Consider linear equation

BL

(^ = L1

(dx) u + f <  x > .

where linear bounded operator B acting from linear space E to E has no inverse operator. Differential operators

l( * )-£ ∂tⁿ

+

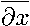
E

k 0+ k 1+-----+ k m< n - 1

L1

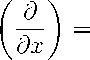
E

k o+ k 1+-----+ k m< n 1

dk o+-----+ km dtk0 dxk1... xm1

n 1 < n.

Here coefficients a_k 0 ... _km : D C R ^{m +1} ^ R¹ , b_k 0 ... _km : D C R ^{m +1} ^ R¹ are sufficiently smooth and defined in D , 0 G D . The domains of definition of operators L , L1 consist of linear manifolds E d of sufficiently smooth functions in D with their values in E, which satisfy certain system of homogeneous boundary conditions. An abstract function f : D C r m +¹ ^ E _of argument x — ( t, x 1 ,..., x_m ) is assumed to be given and the problem is to find the solution u : D C R ^{m +1} ^ E_d.

The operator B is assumed to be independent of x. If the оperator B lias an inverse bounded operator then equation (1) is called regular and otherwise it is called irregular equation. If E = R N a nd det B = 0 , then (1) is the system of linear partial differential equations (PDE) of Kovalevskaya type, and we have a well known regular problem of the PDE theory. The foundation of many branches of modern general theory of PDE systems was constructed by EG. Petrovskii [1]. In regular case the initial conditions for (1) can be defined as follows

_∂ i _u ∂tⁱ

= ф i ( x 1 ,..., X m ) , i = 0 , 1 ,...,n - 1 . (2) t =0

Here functions ф_i are analytica 1 functions in D . If f is an analytic function of t, x 1 ,... ,x_m in D , then the Cauchy problem (1), (2) is not only solvable but also well-posed in class of analytic functions.

The well-posedness of the Cauchy problem is a challenging issue even for linear PDE systems in spaces of non-analytic functions. They are usually solved in a class of functions satisfying certain estimates [1].

Irregular models enable study of systems behavior in critical situations [2]. At present, the basis of relevant theory is constructed for certain classes of ecpiations. For example, the theory and numerical methods for differential-algebraic equations has been constructed.

The intensive studies of more complex theory of irregular PDE and abstract irregular differential operator equations are conducted but there are still a lot of unexplored problems.

If B is a normally solvable operator, x E R¹ then the approach in the theory of equations of the form (1) can be based on the splitting of the Banach space into a direct sum in accordance to Jordan structure of the operator B [3-5] and G.A. Sviridyuk’s results from the theory of semigroups with kernels [6]. These approaches are applied to various problems [7,8].

In this field analytical methods were proposed for constructing classical and generalized solutions of the Cauchy problem for ordinary operator-differential equations with x E R¹ in Banach spaces with irreversible operator in the main part.

The theory of irregular operator-differential PDEs in Banach spaces in the multidimensional case with x E R ⁿ, n >  2 , is to be constructed. There are only initial results in this field published in preprints. Therefore, the construction of the general theory of equations of the form (1) with irreversible operator B is of theoretical interest. It is also important for the state of the art mathematical models of compex systems [2,9,10].

It is to be outlined that classical initial Cauchy conditions (2) for equation (1) play very limited role. Indeed, because of the irreversibility the operator B time direction is characteristic and functions ф_i can not be arbitrary selected in the initial conditions (2)! Then there appears a question of reasonable formulation and methods of solution of non-classic boundary problems, taking into account the structure of the operator B . The objective of the present work is to solve this problem. In Sec. 2 and Sec. 3 this problem is solved for irreversible operator B which enjoy skeleton decomposition B = A1A2 , where Ai E L ( E ^ E 1) , A2 E L ( E 1 ^ E ) , and E 1 is a, normed space.

The remainder of the paper is organized as follows. Sec. 1 presents an introduction concerning the skeleton chains of linear operators using results [4]. The concept of regular and singular skeleton chains is introduced. It is proved that the operator B must be nilpotent in case of singular skeleton chain. In Sec. 2 it is assumed that the noninvertible operator B generates a skeleton chain of 1 inear operators of finite length p and it Is demonstrated that irregular equation (1) can be reduced to the recurrent sequence of p + 1 equations. It is to be noted that each equation of this sequence is regular under the natural restrictions on differential operators L, L1 and certain initial-boundary conditions. Therefore if the operator B has a skeleton chain of length p then the solution of irregular equation (1) can be reduced to a regular system from the (p + 1)-th equation.

The proposed approach can be employed for wide range of concrete problems (1) due to finite length of the skeleton chain of the finite-dimensional operator B .

The formulas connecting the solution of (1) with the solution of reduced regular system are derived. This result allows us in Sec. 1 to set new well-posed non-classic boundary conditions for (1) for which the equation enjoys a unique solution what is demonstrated in Sec. 2. For applications, it is important that this solution can be found by solving the sequence of regular problems proposed in this paper. Corresponding results and examples are given in Sec. 3 and Sec. 4.

1.    Skeleton Chains of Linear Operator

Let B G L ( E ^ E ) , arid B = A 1 A 2 , where A 2 G L ( E ^ E 1) , A i G L ( E 1 ^ E ) , arid E 1 , E are linear normed spaces. The following definitions can be introduced.

A decomposition B = A ₁ A 2 is called a skeleton deeoinposition of the. operator B . Introduce a linear operator B ₁ = A 2 A ₁ . Obviously B ₁ G L ( E 1 ^ E 1) . If the operator B ₁ has a bounded inverse or it is null operator acting from E 1 10 E 1 , then B generates a skeleton chain { B ₁ } of length 1. Then the operator B ₁ can be called a skeleton-attached operator to the operator B . This chain is calied singular if B₁ = 0 and regular if B₁ = 0 . If B ₁ is an irreversible non-null operator then it is assumed to have a skeleton decomosition B ₁ = A 3 A 4 , where A 4 G L ( E 1 ^ E 2) , A 3 G L ( E2 ^ E 1) , and E2 is new linear normed space. Obviously in this case A 2 A ₁ = A 3 A 4 and an operator B ₂ = A 4 A 3 G L ( E2 ^ E 2) can be introduced. If it turns out that B₂ has a bounded inverse or B₂ = 0 , then B has a skeleton chain { B ₁ , B ₂ } of length 2. The chain { B ₁ , B ₂ } is singular if B ₂ = 0 arid regular otherwise. Also, the third case is possible: operator B₂ is irreversible non null operator. Then chain length is greater than 2 and one should continue chain’s construction.

Indeed, this process can be continued for a number of linear operators by introduction of the normed linear spaces E i , i = 1 ,... ,p and by bounded operators construction A2 i G L ( E i - 1 ^ E i ) , A 2 i - 1 G L ( E i ^ E i - 1) , which satisfy the following equalities

A 2 i ^A2 i - 1 = ^A2 i +1^A2 i +2 , i = ¹ , ² , . . . ,p ^{— 1} . (3)

Equation (3) defines a sequence of linear operators { B ₁ ,..., B _p} as follows

B i = A 2 i A 2 i — 1 , i = 1 , 2 ,...,p. (4)

Obviously B i G L ( E i ^ E i ) . Here the operator B _p either lias a bornided inverse or B _p is a null operator acting from E p t0 E p . This process can be formalized as the following definition.

Definition 1. Let B = A ₁ A 2 and operators { A }== ₁ satisfy (3). Let operators { B ₁ ,..., B _p} be defined by (4), operators { B ₁ ,..., B _{p- 1} } be noninvertible, and operator B _p have, a bounded inverse or be■ a null operator acting from Ep 10 Ep. Then the. operator

B generates a skeleton chlain of linear operators { B1 ,..., B _p} of length p. If B _p = 0 then the chain is regular, if B _p = 0 then the. chain is calk-d singular. Operators { B1 ,..., B _p} are called skeleton-attached to operator B .

The most important linear operators generating skeleton chains of the finite lenghts are given below:

• 1.    Let E = R m, then a square matrix B : R m ^ R m with det B = 0 obviously has skeleton chain { B1 ,..., B p} of decreasing dimentions. The final matrix B _p will be regular or null matrix, det B i = 0 , i = 1 ,... ,p — 1 .

• 2.    Let E be an infinite dimentional нотred space, then a finite operator B = ’^•YnZiOn i =1

n

where {zi} E E, zi E E* h^{as a} skeleton chain consisting of finite number of matrices { B1 ,..., B p} of decreasing dimentions. Here B1 = ||(zi,7j)||”j =1 is the first element of this chain, det B i = 0 , i = 1 ,... ,p — 1 • B _p is a, null inatrix or det B_p = 0 .

Here according to Definition 1 the length of the chain p = 1 if det[ (zi,7j) ] nj =1 = 0 or (zi,7j) = 0 ,i,j = 1 , 2 ,... ,n. In general case the chain always consists of finite number of matrices.

Using (3), (4) and Definition 1 the following result can be formulated.

Lemma 1. If the operator B has a skeleton chain of length p then

^B n = A1A3 • • • A2 n- 1^B n- 1A2 n-2A2n- 4 • • • A2 • ⁿ = ¹ • • • • ^,p + ¹ •           00

where. B1 , B₂ ,... B _p are. elements of the skeletoil chain of the operator B •

From Lemma 1 it follows

Corollary 1. If the operator B has a singular skeleton chain of length p, then B is a nilpotent operator of index p + 1 •

To proof the Corollary it is sufficient to put n = p + 1 and demonstrate that B ^{p +1} is a null operator because B _p is a null operator due to the above introduced definition of a singular skeleton chain.

2.    Reduction of Abstract Irregular Equation to the Sequenceof Regular Equations

The operator B and linear operators { A i}^ 1 from a skeleton chain of the operator B are assumed to I>e independent of x and commutative witli linear operators L and L1 . In this paragraph for sake of darity it is assumed that operators L and L1 can lie different from the introduced above differential operators L( 1 ) • ^L1( ddx ) and equation can be considered in abstract form

BL u = Li u + f.                              (6)

Equation (1) can be considered as a special case of equation (6). Obviously, the introduced commutativity condition is fulfilled for (1) with linear operator B independent of x and introduced differential operators ^L( d ) • Li( dx ) •

Let us reduce equation (6) to a system of p + 1 equations which are regular in certain conditions imposed on operators L , L _i . Let us start with the simple case when p = 1 . Introduce a system of two equations

B 1 L u i = L i u i + A 2 f,                              (7)

L i u = —f + A i L u i .                              (8)

where u G E and u 1 G E 1 . The decomposed system (7) - (8) can be obtained by formal multiplication of (6) by the operator A2 from the skeleton decomposition of the operator B and niaking notation u 1 = A 2 u.

It is to be noted that system (7), (8) is splitted and B_i is an invertible operator. Therefore if the operators B_iL — L_i , and L_i have bounded inverse operators then a unique solution can be constructed. Of course without additional conditions there remains a question: Does a constructed solution u ( x ) satisfy (6) ?

Let us introduce two lemmas establishing the link between (6) and system (7), (8) to answer that cpiestion.

Lemma 2. Let u* satisfy (6) a nd operator L _i have left inverse. Then a pair u i = A 2 u*,u* satisfies (7), (8).

Proof. Based on conditions of the Lemma the following equality is satisfied

A1A2L u* = Liu* + f.(9)

From (9) because of commutativity condition the following equality is valid

AiLA2 u* = Liu* + f(10)

and

A2AiLA2 u* = LiA2 u* + A2 f.(11)

The latter equality demonstrates that u* = A 2 u* is a solution of (7). Substitution u i into the right hand side of (8) yields the following equation with respect to u with the known right hand side

L i u = —f + A^L u*.

Here the operators commutativity property is employed. The solution exists for such equation. Indeed, due to (9) right hand side of the equation is equal to L _i u*. Hence for given u* and u i = A 2 u* the right hand side belongs to the range of the operator L _i . Therefore. L _i u = L _i u*. Since the operator L _i has left im"erse. then u* is a unique solution to (8) for u _i = A 2 u*. Lemma 2 is proved.

□ Lemma 3. Suppose that a pair ( u i ,u* ) is a solution to (7), (8). Let the operator L _i have right inverse L f ⁱ . Then element u* satisfies (6).

Proof. The element —f + AiLui belongs to the range of operator Li, because a pair u*, u* satisfies (7), (8). Hence u* = Lfi(—f + AiLui) beeause —f + AiLu* G R(Li), where R(Li) is the range 0f the operator Li. It is to be demonstrated that the constructed element u* satisfies (6) because by hypothesis ui satisfies (7). Indeed, substitution of the constructed u* into (6). where B = AiA2, yields

AiA2LL d ⁱ( —f + AiL u 1) = AiL u*_i.

Taking into account operators commutativity, the following equality is valid

AiL { A2L d ⁱ( —f + AiL u* ) - u*} = 0 .                     (12)

Since A_i and L are linear operators then it remains to verify that in (12) the element in brackets is zero. Since u i G E _i satisfies (7), where B_i = A₂A_i , then the following equality is valid

A2(AiL u i — f ) = Li u*.                             (13)

Hence A₂(A_iL u* — f ) G R (L_i) and u i = L f ⁱA2(A_iL u* — f ) , where L f ⁱ is the right inverse to the operator L_i . Since A₂L_i = LiA₂ then A₂ = L f ⁱA2L_i . This yields A2L f ⁱ = L f ⁱA2L1L /. From equality LL. ' = Iit follows that the right inverse L_iⁱ is also commutative with the operator A₂ . Then (13) can be represented as

A2L ^{f i} (A_XL u i — f ) — u i = 0 .

Thus we have shown that expression in brackets in (12) is zero. Lemma 3 is proved.

□

Let us concentrate on general case of skeleton chain of arbitrary finite length p. We assume operator B to have a skeleton chain { B _i ,..., B _p}, p >  1 , and linear operators {A i }2= _i represent dec-omposition of B i which skeleton is attached to B . Introduce

i ui = ZIA2ju, i = 1 ,...,P,                           (14)

j= where ui G Ei, ui = A2iuifi,u0 := u.

If u 0 satisfies (6) then for p G N by Definition 1 we get equalities

p

Bp L up = L i up + [JA2 j f,(15)

j =

i

Liui = —    A2j f + A2i+iLui+i,(16)

j =

Liu = —f + AiL ui.(17)

For p >  2 there is a connection between the solution of (6) and system (15) - (17). In particular the following two lemmas can be formulated.

Lemma 4. Let u* satisfy (6) and operator L _i have left inverse. Then elements u* = П j =_i A ₂ j u* ,i = p,p — 1 ,..., 1 satisfy (15), (16), and u* satisfies (17).

Lemma 5. Let elements up,up_fi,..., u*, u* satisfy (15) - (17) and operator L _i have right inverse. Then element u* determined from (17) of spitted system (15) - (17) is a solution to (6).

Proof of Lemma 4 and Lemma 5 for any natural number p can be reduced to employment of the skeleton chain via operators { A j } j = ₁ and repeats of stages of the proofs of Lemmas 2 and 3 for the case of p = 1 . Based on Lemmas 1-5 the following main result can be formulated.

Main Theorem. Let irreversible bounded operator B have a skeleton chain {Bi, ...,Bp}. Let oiwrator B p L — L1 have a bounded, inveise with a domain in Ep. Let operator L1 be dejined on domains Ei, i = 1,... ,p and E. Let o]ierator L1 have an inverse bounded operator on Ei, i = 1,... ,p or E. Then system (15) - (17) enjoys a unique solution {up,up- 1, ...,u*, u*}, where p up = (BpL — Li)-1 Цл2jf, j=1

i

u* = L1 1 { — П A2jf + Лj+1Lu*+1}, i = p — 1, • • • , 1, j=1

u* = L ^{- 1} {—f + A 1 L u 1 }.

Moreover, element u* satisjies (6) and u* = H j =₁ Л ₂ ju*,i = 1 ,.. -, P-

By setting the initial-boundary conditions to ensure the reversibility of the operators L ₁ and B _p L — L ₁ with specific differential operators L and L ₁ and using the Main Theorem the existence and uniqueness theorems can be derived. Moreover, the formula obtained in Theorem can effectively build the desired classical solution of (1) with sufficient smoothness of f : Q C R ^{m +1} ^ E and the coefficients of tfie differential operators L and L ₁ . Such applications of the theory are discussed further in section 3.

3.    The Existence and Methods of Constructing Solutions of Nonclassic BVP with Partial Derivatives

Consider the system

B        a k 1 k 2

k 1+ k 2 < n

d^{k 1+ k 2} u ( x, t ) ∂t^{k 1} ∂x^{k 2}

c k 1 k 2

k 1+ k 2 < m

d^k 1^{+ k} 2 u ( x,t ) ∂t^{k 1} ∂x^{k 2}

+ ^{f ( x,}t ) .

Here m < n, B is a constant N xN matrix, det B = 0 , a_k 1 _k 2 , c_k 1 _k 2 are numbers, a n ₀=₀ , a о _n = 0 , c о _m = 0 , c m о = 0 . The vector-functions u ( x,t ) = ( u ₁( x,t ) ,... ,u_N ( x,t )) ^T, f ( x,t ) = ( f ₁( x,t ) ,..., f_N ( x,t )) ^T are supposed to Ire de fined and analytical for —to < x,t <  to .

Let rank B = r < N. Then Irased on [11] B = Л ₁ Л ₂ , where Л ₁ is an N x r matrix. Л ₂ is an r x N matrix. Let us introduce an r x r matrix B ₁ = Л ₂ Л ₁ and assume that det B₁ = 0 . Then taking into account Lemma 3, the solution to (18) can be reduced to the successive solution of (7), (8), which are in this case as follows:

B1

a k 1 k 2

k 1 + k 2 < n

d ^k 1^{+ k} 2 u ₁( x,t ) ∂t^{k 1} ∂x^{k 2}

E

^c k 1 k 2

k 1 + k 2 < m

d^{k 1+ k 2} u ₁( x, t ) ∂t^{k 1} ∂x^{k 2}

+ Л 2 f ( x,t ) ,

c k 1 k 2

k 1 + k 2 < m

d^k 1^{+ k} 2 u ( x,t ) ∂t^{k 1} ∂x^{k 2}

v-         ^d k ¹⁺ k ^{2 u} 1^{( x,t} )

f (x,t )+ Л1 2_^ ak 1 k 2 dtk 1 dxk 2   , k1 +k2

where det B1 = 0, u 1(x,t) = (u 11 (x,t),...,u 1 r(x,t))T,r < N, u 1 = A2u. By hypothesis an0 = 0, c0m = 0, therefore for system (18) one may introduce the initial conditions diu (x, t) ∂xi

= 0 ,i = 0,1,.

x=0

., m — 1,

diu (x,t)

^A2   ∂tⁱ

= 0 ,i = 0, 1 ,...,n — 1.

t=0

The vector-function u 1(x, t) based on Kovalevskaya theorem can be defined as a unique solution to system (19) with initial conditions di u 1( x,t) ∂ti

= 0, i = 0, 1,.

t=0

., n — 1.

By substitution of vector u 1(x,t) into the right hand side оf (20), the desired vector u(x,t) can be found as a unique solution to the Cauchy problem (20), (21).

Consider system

B d^ ) = (dt a²dx 2) u^(X,t) ^{+ f(X,t})’ n -³'               ⁽²³⁾

As in system (18). B is a, shigular N x N matrix лvitli rank B = r < N, B = A1A2, B1 = A2A1, detB 1 = 0. Let f(x,t) = (f1(x,t),...,f_N(x,t))^T be a vector-function defined for 0 < x < 1, 0 < t < to, continuous with respect to x and analytical by t,u = (u 1,..., u_N)^T.

The objective is to construct a solution of (23) in Q = {0 < x < 1,0 < t < to}. Based on Lemma 4 and the Main Theorem introduce system of two equations (u 1 = A₂u)

B1 A = ( d — a2 dx-2 ) u 1( x.t) + A2 f (x,t),(24)

(dt— a25x2)u(x’t, = —f(x,t) + A18 "axx't)

with initial-boundary conditions

AuA-t)   =0,i = 0,1 ,...,n — 1,(26)

i

∂x u (x,t)\t=0 = 0,(27)

u(x, t) x=0 = 0, u(x, t) x=1 = 0.(28)

Since det B 1 = 0 then the vector-function u 1(x,t) based on Kovalevskaya theorem can be defined as a unique solution of Cauchy problem (24) -(26). Substitute u 1(x,t) into the right hand side of (25). A unique solution of the first boundary value problem (25), (27), (28) is constructed for the heat equation using known formula (here readers may refer to p. 215 in [12]), using the source function. The constructed solution u(x,t) will be a classic unique solution of (23) in domain Q = {0 < x < 1, 0 < t < to}. This solution satisfies the initial conditions diu(x,t)            .

A2   TO” = ⁰, i = ¹,...^{,n — 1}

^dx    x=0

and (27), (28).

4.    Skeleton Decomposition in the Theory of Irregular ODE in a Banach Space

Consider the simplest irregular ODE

B ^tT = u⁽¹) ⁺f⁽‘) •                          ⁽²⁹⁾

f (t) : [0, to) ^ E, B G L(E ^ E). Let {B₁,..., B_p} be a skeleton chain of the operator B. Then from the Main Theorem the following results can be formulated.

Theorem 1. Let {B₁,..., B_p} be a regular skeleton chain, the function f (t) be (p — 1)-times differentiable. Then equation (29) with initial condition

П A2ju(t)It=0 = c0, c0 G Ep                            (30)

j=1

enjoys a unique classic solution u0(t, c0). Here u o(t,c o) = —f (t) + Ai “df,                             (31)

where u 1 is defined uniquely (see the Main Theorem).

Let us outline the scheme for construction of the function u₁(t, c0) in solution (31) to problem (29), (30):

• 1.    If p = 1 then u₁(t, c0) satisfies the regular Cauchy problem

• 2.    If p > 2 then the function u₁(t, c0) can be constructed by the following recursion

Г Bi du = u 1 + A2 f (t), ( u 1(0) = co.

BpU = up + П A2j f (t), j=1

up (0) = c 0.

^ui⁽t, ^c0) = A2i+1---+ ^^ ,---- ^— П A2j ^{f (}t)^, i = p -^{1 ,P} -^2, . . . ^{, 1}.

j=1

Theorem 2. Let {B1,..., Bp-1, 0} be a singular chain of length p > 1, 0 is a null operator acting from Ep t0 Ep. Thicn B is a nilpotent operator and the homogeneous equation Bddu = u has only trivial solution. In this case, if the function f (t) is p-times differentiable then the unique classic solution of (29) can be constructed as follows un (t) = —f (t) + B dtun

1⁽t ), ^u 0⁽t) = ^—f(t), ⁿ = ¹,²,...,p.

Here the function up(t) is a unique classic solution of (29).

Conclusion

This paper reports on the novel method of skeleton chains initiated in [4] for the linear operators in order to produce new non-classical boundary value problems for systems of differential and integral-differential ecpiations with partial derivatives arising in modern mathematical modelling.

Acknowledgements. This work is fuilfilled within International Science and Technology Cooperation Program (No. 2015DFA70850) oj China Й Russia; NSEC Grant No. 61673398. The first author’s work is partly supported by RSF Grant No. lf-19-0005f.