Solving school bus routing problem using genetic algorithm-based model

Published Online March 2018 in MECS

School bus routing problem (SBRP) remains a major combinatorial optimization problem which belongs to NP-complete class of problems where the search domain for optimal solutions increases exponentially as the size of problem becomes bigger. School bus routing problem involves the routing of a limited number of school buses along designated routes in an efficient and optimal manner. SBRP seeks to plan an efficient schedule for a fleet of school buses where each bus picks up students from various bus stops and delivers them to their designated schools while satisfying various constraints [1]. The fleet of buses in a school bus routing problem can either be homogenous or heterogeneous. In the former, the school buses have the same capacity while the later have different fleet capacity. The school bus routing problem can be defined as a network N = (V, E) with a set of vertices (school bus stops) V = {0,1,...,и}, and a set of edges E = (i, j) (school routes) that traverses through these bus stops. The traversal cost (cij) of an edge (i, j)e E in terms of distance or time is of paramount importance. The minimization of this traversal cost (cy) is the major goal of finding optimal solution for school bus routing problem.

Solving a typical school bus routing problem seeks to plan an efficient schedule for a limited number of school buses that pick students up from various bus stops and deliver them to their respective schools while satisfying certain constraints (maximum capacity of the bus, minimum riding time of the students and time window to arrive at school). Many researches have imposed a variety of constraints in solving the school bus routing problem. These include; each bus takes exactly one route, each route begins and arrives at the school, each bus stop can be visited by one or more than one bus, the total number of students must be satisfied and the number of students on each bus must not exceed the bus capacity [1]; number of students carried in a bus, total travel time for any student [2]; demand node on a bus, number of vehicle leaving school stop must equal the number of vehicle entering the school, arrival time window at school and number of routes should be less than or equal to the number of buses [3] and so on. There are diverse constraints and assumptions associated with this combinatorial optimization problem. Thangiah and Nygard [2] solved the problem based on an assumption that the number of students that could be picked up by different vehicles would be different. Ripplinger [4]

solved the problem assuming that there are buses that could pick up students with special needs and those that could not pick up those students. Like most of the other existing studies that solved the problem based on one departure point, Thangiah et al [5] presented a solution by considering multi-depots (departure points).

The SBRP is subdivided into five sub-problems including; Data Preparation, Bus Stop Selection, Bus Route Generation, School Bell Time Adjustment and Route Scheduling [6]. Our main focus in this paper is on the bus assignment and route generation. The school bus route generation problem incorporates the search and order of bus stops along designated routes. Various approaches had been used to solve bus route generation problem. Such problems are usually solved by exact methods [7–10] or meta-heuristics which include ant colony optimization (ACO) [11, 12], time savings heuristic and sweep method [13], tabu search [14, 15] and genetic algorithm (GA) [16–18].

GA is a meta-heuristic technique inspired by genetics of real populations. Genetic algorithms in SBRP are implemented with a set of possible route solutions and each solution is known as a chromosome. The algorithm allocates values to a set of individual route solutions based on defined objective function of the problem. It then improves these set of solutions based on the principle of survival of the fittest. To solve the SBRP using genetic algorithms, the various constraints and assumptions of the problem are first analyzed and defined. Next the objective function is set then construction of the initial solution population, genetic operators (crossover and mutation operators) and genetic parameters applicable to the problem follows. In [30] three crossover operators are experimented namely; one-point crossover, two-point crossover and partially mapped crossover. The partially mapped crossover performed better than the other two. In [33], eight crossover operators are assessed on travelling salesman problem.

In this paper, we seek to minimize the number of buses, number of routes and total distance covered by the buses using a genetic algorithm-based approach for a homogenous fleet of buses in a school bus routing problem as seen in our case study (Akure Free School Bus Shuttle Scheme, Nigeria). A number of assumptions and constraints are formulated in Section III in view of solving this problem. The rest of the paper is organized as follows. Section II presents background literature on school bus routing problem and genetic algorithm-based models employed so far, motivating the need for optimal formulation of objective function, constraints and suitable assumptions for the problem. Section III defines the formulation of problem and solution using a genetic algorithm-based approach to achieve the objective function, which includes an assignment phase and routing phase. Section IV presents the results and evaluation of the model while Section V concludes the paper with future areas of research.

• II.    Related Works

This section gives a background review of the school bus routing problem with emphasis on the shortcomings.

• A.    School Bus Routing Problem (SBRP)

The School Bus Routing Problem is an optimization problem which focuses on the efficient use of a fleet of vehicles to transport students from their homes to the school using a given number of buses [19]. This problem falls into a larger class of the Vehicle Routing Problem. It can either be categorized as the Capacitated Vehicle Routing Problem (CVRP) or Vehicle Routing Problem with Time Windows (VRPTW), which are all known to be NP (Non-deterministic Polynomial) hard. Dynamic vehicle routing problem is solved using ant colony optimization with immigrants schemes in [31]. The School Bus Routing Problem is solved when various constraints such as maximizing capacity of the bus, minimizing riding time of students, and time window to arrive at school are satisfied [6]. School Bus Routing Problem has two separate but interrelated routing issues: assigning students to their respective bus stops and routing the buses to the bus stops. The goal of solving the School Bus Routing Problem is to find optimal school bus routes. This can be achieved by minimizing the number of buses, the number of different routes, the total distance accumulated among all routes, the duration of the longest route and the distance that students have to walk from their homes to and from their stops.

Researches on solving school bus routing problem using exact and meta-heuristic approaches seeks to minimize the objective function whilst imposing variants of constraints and assumptions on the formulation. Various literature reports notable findings in this area of study. Berger and Barkaoui [23] presents a hybrid genetic algorithm for the capacitated vehicle routing problem (VRP). Two populations of solutions are generated concurrently using a random procedure to construct feasible solution individuals. Genetic operators are also used in combining variations of key concepts derived from other VRP (with time-variants) techniques. The result shows that hybrid genetic algorithm for VRP is cost-effective and very competitive when compared to the best-known VRP meta-heuristics. Because of limited computational resources, parameter values are determined empirically over a few intuitively selected combinations. A real-life School Bus Routing Problem is modelled as a classical Capacitated Vehicle Routing Problem (CVRP) [12]. The work aims to increase utilisation of buses and to reduce transportation time using ant colony optimization approach. The algorithm need improvement in travel times and reduced costs. Díaz-Parra et al. [24] presents a solution to the School Bus Routing Problem by applying bio-inspired algorithm in the vertical transfer of genetic material to offspring. The genetic algorithm uses clusterization population preselection operator, tournament selection, crossover-k operator and an intelligent mutation operator called mutation-S. The solution is yet to be tested in a real life situation.

Kim and Park [3] propose a model for solving School Bus Routing Problem (SBRP) using heuristic algorithm based on harmony search. The model is formulated as a mixed integer programming problem. Harmony Search is the heuristic approach used and commercial optimization package (CPLEX) is used as an exact method in order to validate the model. It reported that Harmony Search produced the same result with exact method in a very short period of time, therefore providing a good solution to the problem. However, the model only considers a single depot and not multiple depots as we have in the real world. Also, there is no guarantee that optimal solution would be obtained through Harmony search as the size of the network increases. In [25] School bus routing: A case study of Wood Bridge School Complex, Sekondi-Takoradi, Ghana is presented. It formulates school bus routing as a single-objective problem (integer programming mode) utilizing ant colony meta-heuristic approach. Distances between pick-up points are recorded using a car; distances collected and coded using MATLAB. The total cost of transportation is reduced by 32%. This approach requires much complexity on time.

Abdul, and Faruque [26] presents a solution to vehicle routing problem using genetic algorithm. In this work, the heuristic method is used to implement an algorithm that inserts new elements as a sub-route and also one, which does a simple sequence-based crossover. Findings show that if a very high heuristic level is used, fast good results were obtained. Therefore, system is tuned to have a balance between finding fast a solution and limiting the search space . The choice of the crossover method is quite intuitive. In [1], a novel geographic information systems (GIS)-based decision making framework that combines GIS, clustering techniques, network cutting techniques, and a hybrid ant colony optimization meta-heuristic with the iterated Lin–Kernighan local improvement heuristic is proposed for solving the SBRP as a split delivery vehicle routing problem (SDVRP). In formulation of the SBRP as a SDVRP, a set of homogeneous school buses are designed to serve a set of students (at bus stops). Each of these bus stops can be traversed more than once, and the number of students of each bus stop can be greater than the capacity of the buses. There was no imposed constraint on the number of available buses. This novel approach is a first step toward a fully integrated spatial decision support system (SDSS) that could be used to solve the different SBR sub-problems using a high computational approach.

The authors of [27] present genetic-based algorithm to solve three of the five sub-problems of SBRP, including bus stop selection, bus route generation and route scheduling. The result achieves minimization of overlapping routes in the study. An exact and metaheuristic approach for a bi-objective school bus scheduling problem is presented [28]. The objective of the proposed framework is to minimize the number of buses and total travel distance travelled. The model incorporates a local search procedure coupled with simulated annealing. The local search operators, such as one-point move, two-point move, 2-opt move and cross- exchange, are used to enhance the route solution gradually. Based on this algorithm, the two-stage metaheuristic solvers for bi-objective school bus routing problem or school bus scheduling problem are designed. It is seen that in the local search operations, some solutions that make route length longer by simulated annealing are accepted, but may escape from local optima and realize the search in depth and diversification. A probability model to solve the school bus routing problem with stops selection is presented by Ricardo and Arturo [29]. The authors present fundamental contribution by using a probability model to describe the feasible solution space distribution and best solution. The paper provides an alternative to solve permutation-based representation problems using logistics application. An estimation of distribution algorithm is used to solve the combinatorial optimization solution of a SBRP. The run-time difference between the probability model and genetic algorithm is less significant.

The case study of Akure free school bus shuttle scheme, Nigeria gives a description of the school bus routing problem.

• B.    Free School Bus Transportation in Akure

Akure is one of the southwestern cities in Nigeria, West Africa. Students are transported to school through various means. Some students walk to school, some through public transports (taxi cabs/ motor cycles), or private cars. Majority of students make use of the free bus shuttle provided by the state government as a means of transport to and from their schools. The free school bus shuttles in Akure (Ondo State), Nigeria are operational during week days. These buses pick up students in the morning at designated bus stops, while the students drop off at bus stops that are closest to their schools. In the afternoon, the students join the buses at the bus stops and drop off at bus stops closest to their homes. All buses are homogenous, that is they are of the same capacity. The buses can accommodate a maximum of one hundred (100) students.

The school bus routing problem is one of the problems facing many cities in the world. The free school bus shuttles provided by the government of Ondo state, Nigeria to students in Akure metropolis is means of assisting parents. Routing these buses is presently planned intuitively, that is, routing is carried out with skill but without appropriate planning in real life, which may result in excessive cost for the free transport scheme. The existing routing pattern from the case study and from several reviewed literature [3, 12, 19] has shown that buses assigned to a particular route picks up students at designated bus stops along the route and only stop when they reach the final destination. This leads to creation of many routes, increase in the number of buses in use and several buses navigating the same route. More cost is incurred due to the manual routing method. There should be provision for students stopping at any bus stop. There is therefore a need to route the school buses in the most efficient way by minimizing the number of routes and the total number of buses en-route.

• C.    Existing Routing Pattern

From several literatures on SBRP and the case study, it is discovered that the existing routing pattern involves a traverser (bus) from a starting point to the destination point. There are several start positions (S1, S2, S3) of school buses but there is only a single destination point (D) where all the students are dropped. A typical graph representation of the scenario is presented in Fig. 1.

There are no school stop points for the students and none of the students are picked or dropped until the destination point is reached. The various routes are represented by (r1,…,r5) as shown in Fig 1.

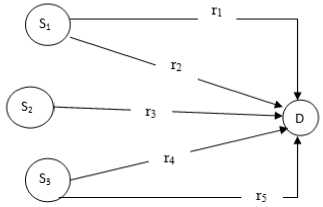
Fig.1. A typical representation of the existing SBRP scenario.

• D.    Genetic Algorithm

Due to the NP-hardness of the school bus routing problem, meta- heuristic techniques could be used for solving the problem. Even though optimal solutions can be obtained through the use of exact methods (branch and bound, dynamic programming, integer programming, etc.), meta-heuristic techniques produces optimal or near optimal solution in a reasonable amount of computational time. Genetic algorithm has been widely used to solve several combinatorial optimization problems, among which is the school bus routing problem [17], optimal allocation of project supervisors to students [30], optimal allocation of devices to control power line flows [32]. It is used for determining the best solution out of many possible solutions. Genetic algorithms are among the several types of meta-heuristics that randomly search for good solutions to specified problems. Some other solution methods include tabu search, simulated annealing and ant colony optimization [20]. Genetic Algorithms differ from traditional search and optimization algorithm in the following ways [21]:

• a.    They work with a coding of solution set, not the solution themselves.

• b.    They search from a population of solutions, not a single solution.

• c.    They use fitness function not derivatives or other auxiliary knowledge.

• d.    Genetic Algorithms use probabilistic transition rules, not deterministic rules [22].

Selection of initial population solution, application of crossover on solution routes and mutation operation on the set of routes closest to the fitness function plays an important role in arriving at an optimal solution.

• III.    Proposed Model

• A.    Problem Formulation

The school bus routing problem is represented in form of a graph (1).

G = ( P , R )                   (1)

where P is the set of nodes (pickup points) and R is the set of arcs (or routes) in the graph. Each node represents either the pick-up point where students are picked up in the morning or the drop off point where students disembarked in the afternoon. An arc corresponds to the route to be visited from node i to j (r ij ). The objective function aims at minimizing the number of buses in use and to find optimal routes, hence minimizing cost. To achieve the stated objectives, the following assumptions are presented:

• a.    Each route has a maximum of two buses allocated to it.

• b.    One of the buses allocated to a route starts from the source while the other starts from the destination point.

• c.    A student is permitted to take more than one bus to get to his/her destination (school), that is, a student drops from a bus at a particular stop and enters another bus to get to his/her school.

• d.    All buses have the same capacity.

• e.    The maximum capacity of a bus is not exceeded.

• f.    A road or path is not navigated more than once.

• B.    Solution

The model is divided into two phases namely, the assignment phase and the routing phase. The assignment phase solves the problem of assigning the available school buses (β) and pick-up points (P) to routes (R), while the routing phase is carried out using genetic algorithm to determine the best route to the destination.

k | 1,If Bus k Travels Route ij ij 1 0, otherwise

where k E P , i G F n , j E P_O ut

P in and P out are pick up points that permit inflow and outflow (school bus stops).

• C.    Assignment Phase

The assignment phase parameters are stated thus, let R represents the set of available routes, P represents the students’ pick-up points along a particular route, such that;

^P = ^{ P 1 , p 2 , p 3 ,...,P n ^{}                  (4)}

where n is the total number of pickup points in a route. Let C represents the capacity of each bus, Mij represents the maximum number of students at a pick-up point j in route i, Si represents the number of bus stops in a route Vi represents the number of students stopping at a bus stop point in a route ri while β denotes the number of buses assigned to a route ri such that,

5 = {si 1, si ,2, si ,3,-s, n }(5)

D represents the set of distances between pick-up points and can be represented as;

The bi-objective functions are thus,

Enn

MU-X V s в=   j"*   r s=1 "*(7)

Ci

n

Ti.=X(dJ+ ti(8)

T i represents the total distance covered along a route, t i is the distance from the last pickup point to the final destination.

• D.    Routing Phase

The Routing phase involves the application of Genetic Algorithm in solving the bi-objective functions. This phase calculates the best route that each of the buses takes from a particular source (i) to a destination (j). The following steps are taken:

• 1.    An initial population is selected. The population in this case is the several possible routes that exist between a starting point (source) and a destination (stop point).

• 2.    Crossover takes place when new offspring emerge from the combination of several paths in various routes to form a new route r i .

• 3.    The fitness function value T ^f is obtained from the shortest route distance and the set of total distance for possible route x is represented as

x = { 7 1 , T 2 , Т з ,...Т п }                  (9)

And φ represents the function that returns the shortest distance from the set is expressed as,

Т/ = ^ ( x )

A quarter of the total route whose distance is closest to Tif (fitness function value) is selected and mutation is performed on them to produce new sets of routes. The route with the shortest distance is then selected from the new set of generated routes. This is compared with the earlier shortest route distance, Tif . If the new distance is shorter than the earlier one; it then becomes the new fitness function value T f thereby overriding the former one.

• E.    Proposed Routing Pattern

Fig. 2 shows a hypothetical representation of the proposed routing pattern.

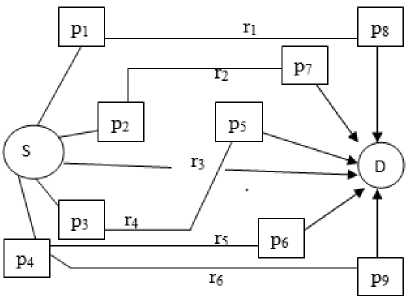
Fig.2. Hypothetical representation of the proposed routing system.

The proposed routing pattern involves a starting point (S), bus picking up students at their designated bus stops (p) and terminates at designated bus stops closest to their schools (school stop points). When these students are dropped off, other students waiting at the bus stop gets into the bus and this is repeated until the bus gets through routes (r) to the end of its destination (D).

• IV.    Implementation Results And Evaluation

• A.    Data Acquisition

The data for our case study (Akure Free School Bus Shuttle) is sourced from the Ondo State Ministry of Transport, Akure, Nigeria. It includes: the capacity of the buses, the number of buses in use, the total number of buses allocated to each of the routes, the list of available routes and the list of designated bus stops. There are currently eight (8) routes in Akure metropolis into which the buses are distributed. Table 1 shows the names of the routes, their starting and destination points and the number of buses allocated to each of the routes. The total number of buses is twenty- one (21).

Along each route, there are designated bus stops provided by the government where students are picked up and dropped off. Distances between the bus stops were recorded manually using the speedometer of the buses. The distance is measured in kilometer (km) by calculating the distance between the current bus stop and the previous bus stop. This procedure is repeated to get the distance for all the designated bus stops.

• B.    Application of Doubly Link List

Doubly linked list is a form of data structure which contains links to the next and previous nodes. The existing roads/paths were numbered serially; these numbers were used as pointers to previous road and to the next road. In the existing routing pattern, it was discovered that there exists repetition of roads, that is, several buses navigating the same road and this does not help to optimize cost. To find the optimal paths for all the routes, doubly linked list was used in such a way that each road/path is linked to a path before it (previous) and to the next path. Therefore, when genetic algorithm is applied, it generates several possible paths with the aid of the doubly linked list by picking the roads at random and using the pointers to generate new roads/paths.

• C.    Implementation Results

The proposed genetic based algorithm model for solving school bus routing problem is implemented in C# on an Intel 1.6GHz machine of 2GB RAM. A total of seventy four nodes (bus stops) are used in the model implementation. Tables of the routes are generated when the user of the application selects a particular node. Any selected node acts as the starting point while the system selects the destination point by itself. The tables are made up of five columns namely: Routes (details of routes generated when a node is selected), total nodes covered (the number of bus stops covered for the selected node), generation (the number of generated routes for that particular traversal) and crossover probability (derived by dividing the total nodes covered for a traversal by the overall total nodes (74)).

Several routes are generated from the genetic model system. Four best routes are selected which include: Emeruku to Oke-Aro junction, Adofure to Oando/Danjuma, Alakure to Oke-Aro Junction and Adebowale to Oke-Aro routes respectively. For each of the selected nodes (bus stops), eighty four (84) routes are generated out of which three are selected based on total distance (shortest), number of nodes (highest) covered and their crossover probability. The fitness function value is the total distance covered for the route that has the highest number of nodes covered. Tables 2, 3, 4 and 5 show a tabular presentation of the results.

Table 1. Available Routes

Route	Starting Point → Destination Point	Number of Buses
ROUTE 1	ADOFURE → ITA-ONIYAN	4
ROUTE 2	ROAD BLOCK → OBA-ILE	4
ROUTE 3	AGBOGBO → ARMY BARRACKS	3
ROUTE 4	MEGA SCHOOL → IJOKA	3
ROUTE 5	IJOMU → ARAROMI	2
ROUTE 6	FIWASAYE → IJOKA	2
ROUTE 7	OLD GARAGE → IJOKA	2
ROUTE 8	HAGARI → IRESE	1

Source: Ondo State Ministry of Transport, Akure, Nigeria.

After selection of best routes for the four best selected nodes, generated routes with highest number of nodes covered and least total distance are selected as the best route. Thus, Alakure to Oke-Aro junction phase is presents overall best route having 69 nodes covered, total distance of 34.5km and 0.93 crossover probability. Table 6 shows a summary of the best routes while Fig. 3 shows a chart of the best routes.

Table 2. Analysis of Result obtained from emeruku to oke aro junction

Nodes covered	Total Distance (km)	Crossover Probability	Fitness Value
61	32.6	0.82
54	27.4	0.73
61	32.7	0.82
			32.6

Table 3. Analysis of Result obtained from adofure to oando / danjuma bus stop

Nodes covered	Total Distance (km)	Crossover Probability	Fitness Value
61	32.6	0.82
61	32.7	0.82
			32.6

Table 4. Analysis of Result obtained from alakure to oke aro junction

Nodes covered	Total Distance (km)	Crossover Probability	Fitness Value
69	34.5	0.93
67	32.9	0.91
69	36	0.93
			34.5

Table 5. Analysis of Result obtained from adebowale to oke aro junction

Nodes covered	Total Distance (km)	Crossover Probability	Fitness Value
61	32.6	0.82
54	27.4	0.73
61	31.1	0.82
			31.1

Table 6. Overall Analysis of Best Routes

Route	Nodes covered	Total Distance (km)	Crossover probability
Emeruku → Oke Aro Junction	61	32.6	0.86
Adofure → Oando/Danjuma	61	32.6	0.82
Alakure → Oke-Aro Junction	69	34.5	0.93

• D.    Performance Evaluation

The performance evaluation is carried out based on two major metrics namely minimum distance and run time. The total distance is obtained by the summation of all the distance values between the nodes (bus stops) within the route. The result of the comparison between our genetic-based model and neural network model for solving this SBRP is represented in Fig. 4 to 7. Fig. 4 shows a comparative advantage of our proposed genetic model to artificial neural network model for route Emeruku to Oke-aro junction. This comparison is based on total travel distance, run time of the routing algorithm and the number of iteration(s) between GA and ANN.

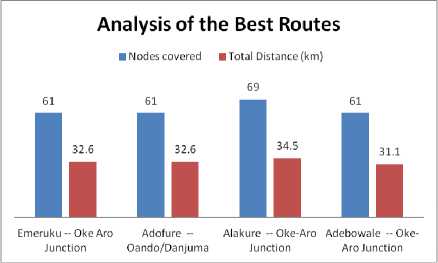
Fig.3. A chart of the overall best routes.

Comparative Analysis for Emerukuto Oke-AroJunction Bus Stop

• ■    Genetic Algorithm ■Artificial Neural Network

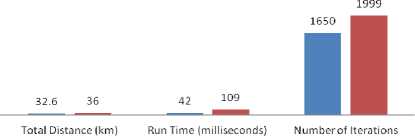
Fig.4. Comparison between GA and ANN based on total distance, runtime and iteration times for route Emeruku to Oke-Aro junction.

Comparitive Analysis for Adofure to Oando/Danjuma Bus Stop

• ■    GeneticAlgorithm ■Artificial Neural Network

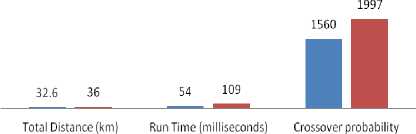
Fig.5. Comparison between GA and ANN based on total distance, runtime and iteration times for route Adofure to Oando/Danjuma junction.

Comparative Analysis for Alakureto Oke-aroJunction

• ■    Genetic Algorithm ■ Artificial Neural Network

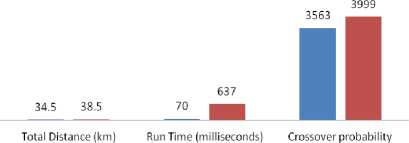
Fig.6. Comparison between GA and ANN based on total distance, runtime and iteration times for route Alakure to Oke-Aro junction.

Fig. 5 shows the comparison between GA and ANN based on total distance, runtime and iteration times for route Adofure to Oando/Danjuma. Fig. 6 compares the GA and ANN based on total distance, runtime and iteration times for route Alakure to Oke-aro junction. Fig. 7 evaluates the performance of the GA and ANN in generation route Adebowale to Oke-Aro junction.

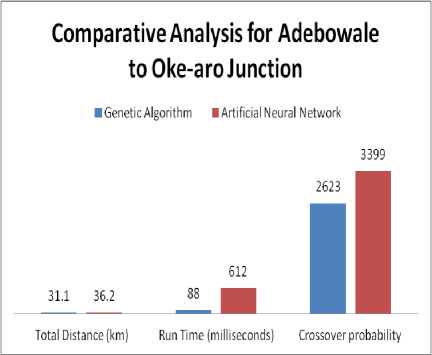
Fig.7. Comparison between GA and ANN based on total distance, runtime and iteration times for route Adebowale to Oke-Aro junction.

• V . Conclusion

In this paper, we present a homogenous school bus routing problem with a set of constraints and assumptions to be satisfied. In order to provide optimal solution to the multi-objective function of the SBRP, we implore a genetic algorithm-based approach to solve a real life problem as seen in the case study (Akure Free School Bus Shuttle, Akure, Nigeria). Data on the capacity of the buses, the number of buses in use, the total number of buses allocated to each of the routes, the list of available routes and the list of designated bus stops is sourced from Ondo State Ministry of Transport, Akure, Nigeria.

To find the optimal paths for all routes, doubly linked list is used in such a way that each path is linked to a path before it (previous) and to the next path. This is because in the existing routing pattern, it is discovered that there exists repetition of routes. That is, several buses navigating the same route thereby leading to congestion and high cost. Our approach first assigns parameters to the formulated assumptions and constraints then carries out the routing by application of genetic heuristic to the set of initial and optimized route solutions. This approach achieves optimal routes, thus routes with the shortest distance and highest number of bus stops (nodes) covered in a traversal are achieved. This work is able to minimize the number of buses, routes and total distance covered by the buses whilst ensuring maximum coverage of bus stops (nodes) along a traversal in less time. The results show that there can be less number of buses in use and reduced number of routes into which the buses are assigned in a homogenous school bus routing problem.

Future areas of research in solving school bus routing problem are inclusion of school time window constraint and application of other hybrid meta-heuristic approach.

Appendix A. Graphical Representation of the Best Route

Appendix A shows a graphical representation of the best route (Alakure to Oke-Aro junction) showing all the nodes (69) covered along a 34.5 km route achieved under a crossover probability of 0.93.

Acknowledgment

The authors wish to thank Ondo State Ministry of Transport, Akure, Nigeria for providing the necessary data for this research.