Some Results of Intuitionistic Fuzzy Soft Matrix

The theory of fuzzy sets introduced by Zadeh[1], showed meaningful applications in many field of studies. This idea of fuzzy sets is welcome because it handles uncertainty and vagueness which the Cantorian set cannot deal with. Fuzzy set has membership function which assigns to each element of the Universe of discourse, a number from the unit interval [0, 1], to indicate the degree of belongingness of the set under consideration. In the fuzzy set theory, the membership of an element to a fuzzy set is a single value between zero and one. But in reality, it may not always be true that the degree of non membership of an element in a fuzzy set is equal to one minus the membership degree because there may be some hesitation degree as well. Therefore, a generalization of fuzzy set was realized by [2], as intuitionistic fuzzy set which incorporated the degree of hesitation known as the hesitation margin (and is defined as 1 minus the sum of membership and non membership degrees respectively)

Intuitionistic fuzzy sets as generalization of fuzzy sets can be useful in situation when the description of a problem by linguistic variable, given in terms of membership function only seems to be too difficult to handle. For example, in decision making problem particularly in the case of medical diagnosis, sales analysis, new product marketing, financial services etc, there is a fair chance of a non null hesitation part in each moment of evaluation of an unknown project. To be more precise, intuitionistic fuzzy sets, let us express for example, the fact that the temperature of a patient changes and other symptoms are not quite clear.

In real life situations, most of the problems in economics, social sciences, environment etc, have various uncertainties. However, most of the existing mathematical tools for formal modeling, reasoning and computation are crisp deterministic and precise in character. There are theories namely, theory of probability, evidence, fuzzy set, intuitionistic fuzzy sets, rough sets etc for dealing with uncertainties.

Szmidt and Kacprzyk[3], showed that intuitionistic fuzzy sets are pretty useful in situations when description of a problem by linguistic variable given in terms of membership function only seems too rough. Szmidt and Kacprzyk[4], describes that due to the flexibility of IFS in handling uncertainty, they are tool for a morehuman consistent reasoning under imperfectly defined facts and imprecise knowledge. Atanassov ([5], [6]) carried out rigorous research based on the theory and applications of intuitionistic fuzzy sets.

These theories have their own difficulties as pointed out by Molodtsov[7], and as such the novel concept of soft set theory was initiated. Soft set theory has rich potential for application in solving practical problems in economics, social science, medical science etc. Maji . et.al [8], have studied the theory of fuzzy soft set. Maji. et. al [9], have extended the theory of fuzzy soft set to intuitionistic fuzzy soft sets.

Matrices play a very important role in the broad area of science and technology. However, the classical matrix theory fails to solve the problems involving uncertainties. So there was the need of expressing those uncertainties with fuzzy matrices. Yang and Ji [10], did lot of research on the fuzzy soft matrices and its application in decision making problems.

Broumi. et. al [11], have studied intuitionistic fuzzy soft sets where some some new operations were introduced while defining concentration, dialation and normalization of intuitionistic fuzzy soft sets. Chetia. et.al [12], discussed some results on intuitionistic fuzzy soft matrix theory. Verma. et. al [13], ihas introduced some new results on intuitionistic fuzzy sets by defing some operations/compositions on it. Rajarajeswari. et. al [14], has found some interesting results while dealing with intuitionistic fuzzy soft matrix theory and in applications. Some aspect of these properties can be had from, Dhar [15].

Here in this article, intuitionistic fuzzy soft matrices will be considered and some properties associated with this will be studied.

The paper is organized as follows: Section I is introductory in nature. Section Ii deals with some preliminary concepts which are required in due course of this paper.Section III deals with the properties of transpose of intuitionistic fuzzy soft matrices. Section IV deals with symmetric intuitionistic fuzzy soft matrices and in Section V, the conclusion is provided.

• II.    Denitions and Preliminaries

• 2.1    Definition : Soft set

• 2.2    Definition :Fuzzy soft set

• 2.3    Definition: Intuitionistic Fuzzy soft set

• 2.4    Definition: Intuitionistic Fuzzy soft Matrix

A. The basic definitions of intuitionistic fuzzy set theory that are useful in subsequent sections of this article are discussed here.

Suppose that U is an initial universe P (U) denote the power set of U , E be the set of all parameters and A c E A pair ( f_A , E ) is called a soft set over U and this is defined by the set of ordered pairs ( f A , E ) = {( e , f A ( e )): e e E , f A ( e ) e P(U )} where ^f A ^is a mapping given by f _: E ^ P(U ) . Clearly soft set is a mapping from parameters to P (U).

Suppose that U is an initial universe of discourse and E is the set of parameters which involves imprecise words. Let P (U) denote the power set of U and A c E . A pair ( f , E ) is called fuzzy soft set over U where f is a mapping given by f : E ^ P(U ) .

Suppose that U is an initial universe of discourse and E is the set of parameters. Let P(U) denotes the collection of all intuitionistic fuzzy subsets of U. Let A c E . A pair ( f , E ) is called an intuitionistic fuzzy soft set (IFSS) over U where f_A is a mapping given by f : E ^ P(U ) .

Let U be an initial universe and E be the set of parameters and A c E .Let (f, e) be an intuitionistic fuzzy soft set over U. Then a subset of Ux E is uniquely defined by RA = {(u, e): e e A, u e fA (e)} , which is called relation form of ( f, e) .The membership and non membership     functions     are     defined     by p : U x E > [0,1] and yRx : U x E ^ [0,1] where p :(u, e) e[0,1] and уКд :(u, e) e[0,1] are membership value and non membership value of u e U and e e E .

I^f (p j ,v j ) = ( p _/; ( u , e j \v_Ra ( u , e j )) , ^{we define a} matrix

^[( p ^{, V} j ^)] m x n

⁽ P 11^{, V} 11 )

^{( p} 21 , ^V 21 )

...

. ⁽ M m 1 , ^V m 1 )

^{( p} 12 , ^V 12 )    ...     ^{( p} 1 n , ^V 1 n )

^{( p} 22 , ^V 22 )   ...    ^{( p} 2 n , ^V 2 n )

^{( p} m 2 , ^V m 2 )

...            ...

...   ⁽ И щи ^{, V} mn )

which is called an m x n intuitionistic fuzzy soft matrix ( IFSM )of the intuitionistic fuzzy soft set ( f , e ) over U.

Therefore, we can say that the intuitionistic fuzzy soft set ( f , e ) over U is uniquely characterized by the matrix ^{[ p} j ^{, V} j ^)] m x n .

Example: Let U = { u A , u ₂, u ₃, u ₄} is a universal set and E = { e , e ₂, e ₃, e ₄} is a set of parameters. If A = { e A, e ₂, e ₃} c E and

Then the intuitionistic fuzzy set ( f , e ) is a parameterized family { f _A ( e ₁ ), f _A ( e ₂ ), f _A ( e ₃ )}.

Hence the intuitionistic fuzzy soft matrix can be written as

⁽ P j ^{, v} ij )

(.4,.5)	(.2,.5)	(.6,.1)	(0,1)
(.3,.5)	(.3,.4)	(.5,.4)	(0,1)
(.6,.2)	(.6,.4)	(.3,.4)	(0,1)
_ (.5,.2)	(.3,.2)	(.7,.2)	(0,1) _

• 2.5    Definition: Union of Intuitionistic Fuzzy soft Matrices

• 2.6    Definition: Intersection of Intuitionistic Fuzzy soft Matrices

• 2.7    Definition: Complement of intuitionistic fuzzy soft matrix

• 2.8    Definition: Max-min product of intuitionistic fuzzy soft matrices

• 2.9    Definition: Scalar multiplication of intuitionistic fuzzy soft matrix

Let A = [( p A , v A )], B = [( p B , v B )] e IFSM m x n . Then union of A and B denoted by A ^ B is defined as

^Let A = [( p A , v a )] , B = [( p B , V B )] e IFSM m x n . ^Then intersection of A and B denoted by A ^ B is defined as

A n B = [min( p iA , pp ), max( v A , y ij )] for allⁱ and^j

Let A = [(pA, va )] e IFSMmxn then the complement of A denoted by Ao is defined as

A o = [(v a , p A )] for all i and j.         (5)

Let A = [( µ i^Aj , ν i^Aj )], B = [( µ i^Bj , ν i^Bj )] ∈ IFSM m × n . Then the max-min product of the two intuitionistic fuzzy soft matrices is denoted as A ∗ B is defined as

Let A = [( µ ^A , ν ^A )] ∈ IFSM and k be any scalar.

Then the scalar multiplication of intuitionistic fuzzy soft matrix A by the scalar k is denoted by kA is defined as kA = [(kµA, kνA)] , where 0≤k ≤1, for all i and j.

• 2.10    Definition:

• 2.11    Definition:

Let

A=[(µiAj,νiAj)] , B=[(µiBj,νiBj)]∈IFSMm×n

Then

µ _ij ^A ( x ) + µ _ij ^B ( x ) γ _ij ^A ( x ) + γ _ij ^B ( x )

Let

A=[(µiAj,νiAj)] , B=[(µiBj,νiBj)] ∈IFSMm×n

Then

A$B= {}

• 2.12    Definition: Transpose of intuitionistic fuzzy soft matrix

Let A = [( µ ^A , ν ^A )] ∈ IFSM then the transpose of A denoted by A^T is defined as

A ^T = [( µ _j ^A _i , ν _j ^A _i )] for all i and j             (7)

The properties of transpose of intuitionistic soft fuzzy matrices will be discussed in the following section.

• III.    Properties of Transpose of Intuitionistic Fuzzy Soft Matrix

• A. If A, B and C be three intuitionistic fuzzy soft matrices, then the following properties hold

• i .(A∪B)T =AT∪BT

• ii .( A ∩ B ) ^T = A ^T ∩ B ^T

• iii .(AB)T =BTAT

• iv .( kA ) ^T = kA^T

• v .(( A ∪ B )@ C ) ^T = ( A @ C ) ^T ∪ ( B @ C ) ^T

• vi .(( A ∩ B )@ C ) ^T = ( A @ C ) ^T ∩ ( B @ C ) ^T

Proof of Property i :

Let A = [( µ _i ^A _j , ν _i ^A _j )] , B = [( µ i^Bj , ν i^Bj )] , C = [( µ _i ^C _j , ν _i ^C _j )] be three intuitionistic fuzzy soft matrices. Then

Again

AT = (µjAi,νjAi)

and

BT = (µBji,νBji)

AT ∪BT ={max(µjAi, µjBi), min(νjAi,νBji)

Proof of property ii:

Proof of Property iv:

Let

A =[(µiAj ,νiAj )]

Then

kA = (kµA,kνA)

( kA ) T = ( k ^ A , k v A )

kA = ( k ^ , k v A )

Hence

( kA ) T = kA T

Proof of Property v.

Again

( A u B )@ C = [ L V )]@[( L C , v C )]

If

ABAB

L ij   ^4     jj

,

Then

• LL. + LI-   V - + V-

• (A u B)@ C = [^_Ai_,]

((A и B)@C)T = [j+LjL,v

_T   L A + L C v A +v ^C

(A @ C) T = [   /,]

l B + l C v B + v C

( B @ C) ^T = [ ji    , j^-j ]

LAj + LC ^Lij + L vj +vC ^ vB

,, т          т L a + Li v» + v И

( A @ C ) ^T u ( B @ C ) T = [        , ^-^j- ]

The following numerical example will illustrate the concept clearly.

• B.    Numerical Examples: Let us consider two fuzzy matrices A and B as follows:

  B =	"(.5,.3) (.8,.1) _ (.2,.5)	(.1,.6) (.4,.3) (.3,.6)	(.7,.1)" (.5,.2) (.4,.5) _
  Then we get
  	"(.5,.2)	(.5,.4)	(.7,.1)	1
  A и B =	(.8,.1)	(.4,.3)	(.5,.1)	(8)
  	_ (.5,.2)	(.3,.4)	(.6,.2)	J
  	(.1,.3)	(.1,.6)	(.3,.6)"
  A n B =	(.4,.4)	(.2,.3)	(.5,.2)	(9)
  	(.2,.5)	(.3,.6)	(.4,.5) _

  ( A u B ) T =	(.5,.2) (.5,.4) (.7,.1)	(.8,.1) (.4,.3) (.5,.1)	(.5,.2)" (.3,.4) (.6,.2) _	(10)
  	"(.1..3)	(.1,.6)	(.2,.5)"
  ( A n B ) T =	(.1,.6)	(.2,.3)	(.3,.6)	(11)
  	_ (.3,.6)	(.5,.1)	(.4,.5) _

Again we have

	"(.5,.3)	(.8,.1)	(.2,.5)"
BT =	(.1,.6)	(.4,.3)	(.3,.6)
	_ (.7,.1)	(.5,.2)	(.4,.5) _
	" (.1,.2)	(.4,.4)	(.5,.2)"
A T =	(.5,.4)	(.2,.3)	(.3,.4)
	_ (.3,.6)	(.5,.1)	(.6,.2) _

Then

"(.5,.2) (.8,.1) (.5,.2)" AT и BT = (.5,.4) (.4,.3) (.3,.4) (12) _(.7,.1) (.5,.1) (.6,.2)_ and

(.1,.2)	(.5,.4)	(.3,.6)
(.5,.4)	(.2,.3)	(.5,.1)
(.3,.6)	(.5,.1)	(.6,.2)

	_ (.1,.3)	(.1,.6)	(.2,.5)"
A T n B T =	(.1,.6)	(.2,.3)	(.3,.6)	(13)
	_ (.3,.6)	(.5,.1)	(.4,.5) _

and

Now we shall calculate the product AB of these two intuitionistic fuzzy matrices in the following way

CL = |mii[mint 1, ,5), mint 5, ,8), mint 3, .2)}, min [maxt 2, .3), max(, 4, ,1) ns (.6, ,5)}] ={max(.1,.5,.2),min(.3,.4,.6)} =(.5,.3)

Cu = [roitminl 1, ,1), mint 5, ,4),mint 3, .3)1 min [maxt 2, .6), maxt 4, .3),max [A ,6)}] ={max(.1,.4,.3),min(.6,.4,.6)} =(.4,.4)

Св = [тм[тш[, L .7),п1ш(.5, .5), mint Зм4)1т1п{пш(,2,.1),™С4,.2),п1ах [6,,5)}] ={max(.1,.5,.3),min(.2,.4,.6)}

=(.5,.2)

C:L = [mox[min(,4, ,5)1min(.2,,8),niin(,5,.2)},min [тах(,4,,3),тах(,3,,1),тах(,1,,5)}] ={max(.4,.2,.2),min(.4,.3,.5)} =(.4,.3)

С_й = |mM[min(,4,l),mint2,,4),min(,5,.3)},min [тах(,4,,б),тах(,3,.3),тах (Л^)}] ={max(.1,.2,.3),min(.6,.3,.6)} =(.3,.3)

C2t = |mKr[min(,4,,7),min(,2,,5),min(,5,,4)},min [max(,4,,l),max(,3,.2),max (.1, .5)}] ={max(.4,.2,.4),min(.4,.3,.5)} =(.4,.3)

C31 = [mox[min(, 5, ,5), mint,3,,8), mint 6,,2)}, min [maxt 2,.3),maxt 4,1),max (.2, ,5)}] ={max(.5,.3,.2),min(.3,.4,.5)} =(.5,.3)

Си = [mox[min(, 2, ,5)1min(.3,.4),niin(,4,.3)},min [maxt 2, A.maxt 4, .3),max (.2 J)}] ={max(.2,.2,.3),min(.6,.4,.5)} =(.3,.4)

CM = [mox[min(, 5, ,7),min(.4,.5),niin(,4,.6)},min [maxi 2,1), maxi 4, .2), max (.12)}] ={max(.5,.4,.4),min(.2,.4,.5)} =(.5,.2)

S!2 = [mix [mint, 1, ,4), mint 4,, 2), mint, 3,, 5)}, min [max(. 6, .4) ,max( 3,.3),max (A 1)}] ={max(.1,.2,.3),min(.6,.3,.6)} =(.3,.3)

S21 = [mix [mint, 1,, 5), mint, 4,, 3), mint, 3,, 6)}, min [max(A2) ,max[, 3..4),max [A2)}] ={max(.1,.3,.3),min(.6,.4,.6)} =(.3,.4)

Л; t = [mix [mint. 7,, 1), mint 1,5), mint, 4,, 3)}, min [max(, 1,, 2), max 12, .4), max (A .6)}] ={max(.1,.5,.3),min(.2,.4,.6)} =(.5,.2)

St2 = [mix [mint. 7, ,4), mint 1.2), mint, 4,, 5)}, min [max(. 1, .4) ,max( 2,.3),max (A 1)}] ={max(.4,.2,.4),min(.4,.3,.5)} =(.4,.3)

U,j = [mu[mint. 7,,5), mint, 5,,3), mint, 4,,6)}, min [maxС1,2),maxt2,.4),max [A2)}] ={max(.5,.3,.4),min(.2,.4,.5)} =(.5,.2)

Hence

BTAT

(.5,.3)   (.4,.3)   (.5,.3)

(.4,.4)  (,3,.3)  (.3,.4)

(.5,.2)  (.4,.3)  (,3,.1)

Let us chose k such that

k G [0,1] .Then we have

kA =

(.05,.1) (.2,.2)

(.25,.2)   (.15,.3)

(.1,.15)  (.25,.05)

(.25,.1)  (.15,.2)    (.3,.1)

(.05,.1)    (.2,.2)    (.25,.1)

Thus we get

		'(.5,.3)	(.4,.4)	(.5,.2)"
	AB =	(.4,.3)	(.3,.3)	(.4,.3)	(14)
		_ (.5,.3)	(.3,.4)	(.5,.2) _
And

( kA ) ^T = (.25,.2)   (.1,.15)   (.15,.2)

( AB ) T =

(.5,.3)

(.4,.4)

(.5,.2)

(.4,.3)  (.5,.3)

(.3,.3)  (.3,.4)

(.4,.3)  (.5,.2)

(.15,.3)  (.25,.05)   (.3,.1)

and
		"(.05,.1)	(.2,.2)	(.25,.1) 1
	kAT =	(.25,.2)	(.1,.15)	(.15,.2)	(19)
		_ (.15,.3)	(.25,.05)	(.3,.1) J

Then let us compute B^TA T and if B^T A T = [ D^ ], we get

Иц = [max[niin(, 1,1), mint, 8,,5), mint 2, ,3)}, min [niax(, 3, .2) ,max(, 1, .4) ,max (.5, ,6)}]

={max(.1,.5,.2),min(.3,.4,.6)}

=(.5,.3)

D12 = [mnx[min(, 5, .4), mint, 8, ,2), mint 2, ,5)}, min [maxt 3,4), maxt 1, .3) ,max (.5, ,1)}]

={max(.4,.2,.2),min(.4,.3,.5)}

=(.4,.3)

D15 = [mix [mint. 5, .5) .mint 8, .3), mint 2, .6)], min [maxt 3, .2), maxt 1, .4), max (.5, .2))]

={max(.5,.3,.2),min(.3,.4,.5)}

=(.5,.3)

D21 = [mix[mint 1, .1), mint. 4, .5) ,min(. 3, .3)}, min [max(. 6, .2), maxt 3, .4), max (A .6)}]

={max(.1,.4,.3),min(.6,.4,.6)}

=(.4,.4)

Let us consider three intuitionistic fuzzy soft matrices A, B and C as

’ (.1,.2)   (.5,.4)  (.3,.6)"

(.4,.4)  (.2,.3)  (.5,.2)

(.5,.2)   (.3,.4)  (.6,.2)

_ (.7,.2)   (.6,.1)   (.5,.3) _

"(.5,.3)  (.1,.6)  (.7,.1)"

B= (.8,.1)  (.4,.3)  (.5,.2)

(.2,.5)  (.3,.6)  (.4,.3)

_ (.1,.7)  (.2,.5)  (.5,.2) _

	" (.1,.3)	(.1,.6)	(.3,.6)	(( B @ C )) T
C =	(.4,.4)	(.2,.3)	(.5,.2)		"(.3,.35)	(.6,.3)	(.25,.5)	(.15,-7)"	(25)
	(.2,.5)	(.3,.6)	(.4,.5)	=	(.1,.6)	(.3,.3)	(.3,.6)	(.2,.5)
	_ (.1,.7)	(.2,.5)	(.5,.2) _		_ (.5,.35)	(.5,.2)	(.4,.5)	(.5,.2) _
Then				Hence

		(.5,.2)	(.5,.4)	(.7,.1)
		(.8,.1)	(.4,.3)	(.5,.1)
A U B =
		(.5,.2)	(.3,.4)	(.6,.2)
		_ (.7,.2)	(.6,.1)	(.5,.1) _
( A и B )@ C
	" (.3,.25)		(.3,.5)	(.5,.35)"
	(.6,.25)		(.3,.3)	(.5,.15)	(20)
	(.35,.35)		(.3,.5)	(.5,.35)
	_ (.4,.45)		(.4,.3)	(.5,.2) .
Hence

(A @ C)T и ((B @ C))T "(.3,.25) (.6,.23) (.35,.35) (.4,.45)" (26) = (.3,.5) (.3,.3) (.3,.5) (.4,.3) _(.5,.35) (.5,.15) (.3,.35) (.5,.2) _ and

( A @ C ) ^T n (( B @ C )) ^T

"(.1,.35)		(.4,.45)	(.25,.5)	(.15,.7)"	(27)
=	(.1,.6)	(.2,.3)	(.3,.6)	(.2,.5)
	_ (.5,.6)	(.5,.2)	(.3,.5)	(.5,.3) _

(( A и B )@ C )) T
	"(.3,.25)	(.6,.25)	(.35,.35)  (.4,.45)"
=	(.3,.5)	(.3,.3)	(.3,.5)    (.4,.3)
	(.5,.35)	(.5,.15)	(.5,.35)    (.5,.2)
Again
		" (.1,.25)	(.3,.5)   (.3,.6)"
A @ C =		(.4,.4)	(.2,.3)  (.5,.15)
		(.35,.35)	(.3,.5)  (.5,.35)
		. (.4,.45)	(.4,.3)   (.5,.3) _

IV. Symmetric Intuitionistic Fuzzy Soft Matrix

(21) A.    Let A = [( ^ A , V A )] e IFSM m _x n and if m=n,

^ A = ^ A and V A = V A then the matrix A is said to be symmetric intuitionistic fuzzy soft matrix. In other words, a matrix A will be said to be a symmetric fuzzy soft matrix if A T = A

For example

(22) ' (.1,.2) (.5,.4) (.5,.2) " A = (.5,.4) (.2,.3) (.5,.1) . (.5,.2) (.5,.1) (.6,.2), is a symmetric intuitionistic fuzzy soft matrix.

and

	■ (.3,.3)	(.1,.6)	(.5,.35)"
B @ C =	(.6,.25)	(.3,.3)	(.5,.2)
	(.2,.5)	(.3,.6)	(.4,.5)
	_ (.1,.7)	(.2,.5)	(.5,.2) _

B. Propositions on Symmetric intuitionistic fuzzy soft matrices

Then

(( A @ C )) ^T

" (.1,.3)  (.4,.45)  (.4,.35)  (.45,.45)

=   (.3,.5)   (.2,.3)    (.3,.5)     (.4,.3)

(.3,.6)   (.5,.2)   (.5,.35)    (.5,.3)

• i.    If A and B be two symmetric intuitionistic fuzzy matrix then A U B is again a symmetric intuitionistic fuzzy soft matrix.

• ii.    If A and B be two symmetric intuitionistic fuzzy matrix then A П B is again a symmetric intuitionistic fuzzy soft matrix.

• iii.    If A be a symmetric intuitionistic fuzzy soft matrix then kA is again a symmetric intuitionistic fuzzy soft matrix.

• iv.    If A and B be two symmetric intuitionistic fuzzy matrix then A @ B is again a symmetric intuitionistic fuzzy soft matrix.

• v.    If A and B be two symmetric intuitionistic fuzzy

matrix, then  A$B is again a symmetric intuitionistic fuzzy soft matrix.

• vi.    If A is a symmetric intuitionistic fuzzy soft matrix then  A^TA  and  AA^T  are also symmetric

intuitionistic fuzzy soft matrix.

• vii.    If A and B are symmetric intuitionistic fuzzy soft matrix then  A^TBA  is again a symmetric

intuitionistic fuzzy soft matrix.

• viii.    If A, B and C be two symmetric intuitionistic fuzzy matrix, then   ( A и B )$ C is again a

symmetric intuitionistic fuzzy soft matrix.

• ix.    If A, B and Cbe two symmetric intuitionistic fuzzy matrix, then ( A О B )$ C is again a symmetric intuitionistic fuzzy soft matrix.

• x.    If A, B and C be two symmetric intuitionistic fuzzy matrix, then ( A @ B )$ C is again a symmetric intuitionistic fuzzy soft matrix.

• C.    Proofs of the Propositions with examples

Proof of i

If A and B be two symmetric intuitionistic fuzzy soft matrix then AT = A and BT = B . Now we are to show that A и B is again a symmetric intuitionistic fuzzy soft matrix.

We have

Since	A T = A	and	BT = B   ,	then
A T и B T	= A и B	which	implies	that
( A и B ) )	= A и B

Thus the result follows that if A and B be two symmetric intuitionistic soft fuzzy matrices then A и B is again a symmetric intuitionistic fuzzy soft matrix.

Numerical example

Let A, B and C be three symmetric intuitionistic soft fuzzy matrices such that

' (.1,.2)  (.5,.4)  (.3,.6) '

A =   (.5,.4)  (.2,.3)  (.5,.1)

_v (.3,.6)  (.5,.1)  (.6,.2) ,

	' (.5,.4)	(.6,.3)	(.8,.2) "
B =	(.6,.3)	(.7,.2)	(.4,.6)
	. (.8,.2)	(.4,.6)	(.8,.1) ,

Proof of i

A и B =	' (.5,.2) (.6,.3) (.6,.3)  (.7,.2) v (.8,.2)   (.5,.1)		(.8,.2) > (.5,.1) (.8,.1) }	(28)
( A и B ) T =	=	' (.5,.2) (.6,.3) (.6,.3)  (.7,.2)	(.8,.2) > (.5,.1)		(29)
From which it is c		v (.8,.2)   (.5,.1) lear that	(.8,.1)

(A и B) T = A и B

Proof of ii

We have

(A О B)T = AT О BT

Proceeding in the above manner, the required result can be obtained.

Proof of iii

Let A be any symmetric intuitionistic fuzzy soft matrix and k be any scalar, and then it is to be proved that kA is again a symmetric intuitionistic fuzzy soft matrix.

Given A is a symmetric intuitionistic fuzzy soft matrix, then ц ij = ^ A and ^vy = V A

Here it is to be proven that kA is again a symmetric intuitionistic fuzzy soft matrix. That is to prove that

(kA)T =kA

Now

kA = k m ,v^)

= (ku, kvyA )

Again

It proves iii.

Numerical Example

Let and

	' (.3,.4)	(.5,.4)	(.6,.1) "
C =	(.5,.4)	(.6,.1)	(.4,.6)
	. (.6,.1)	(.4,.6)	(.7,.2) ,

	' (.1,.2)	(.5,.4)	(.3,.6)
A =	(.5,.4)	(.2,.3)	(.5,.1)
	, (.3,.6)	(.5,.1)	(.6,.2)

and k=.5

Then

kA =	(.05,.1) (.25,.2) (.15,.30)	(.25,.2) (.1,.15) (.25,.05)	(.15,.30) ^ (.25,.05) (.30,.1) v	(30)
Again
	' (.05,.1)	(.25,.2)	(.15,.30) ^
( kA ) T =	(.25,.2)	(.1,.15)	(.25,.05)       (31)
	v (.15,.30)	(.25,.05)	(.30,.1)
This shows that

' (.3,.3)

( A @ B ) T = (.55,.35)

, (.55,.4)

(.55,.35)   (.55,.4) ^

(.45,.25)  (.45,.35)

(.45,.35)  (.65,.2)) _v

and the above result shows that intuitionistic fuzzy soft matrix A @ B is again a symmetric intuitionistic fuzzy soft matrix.

Proof of v

If the above two intuitionistic fuzzy soft matrices are considered, then we see that

A $ B =

' GZ05j,08) (Ж4Л2) (V^,^) '

0/30,л/12)  (V.14,V.C6) (V.20,V.06)

(kA) T = kA and hence kA is again a symmetric intuitionistic fuzzy soft matrix.

(7.24,л^12)  G/2O,7.O6) (^Г40,^[O3)

Here

(kA) T = kA

(A $ B)T =

Proof of iv

Let A = ( ^ A , v A ) and B = ( lib , V B )be two symmetric intuitionistic fuzzy soft matrices. Then it is to be proved that ( A @ B ) ^T = A @ B

'(705,7,08) (730,7.12) (724,712)' (730,712) (7.14,7.06) (720,7.06) (7.24,712) (72o,7o6) (74o,7o3)

This implies ( A $ B ) ^T = A $ B and hence A $ B is again a symmetric intuitionistic fuzzy soft matrix.

Here

Proof of vi

Let A be a symmetric intuitionistic fuzzy soft matrix such that

and

u^ + u5

A @ B = ( 'j ^i

^A ij

+ vB

)

' (.1,.2)  (.5,.4)   (.3,.6) "

A =   (.5,.4)  (.2,.3)  (.5,.1)

₄ (.3,.6)   (.5,.1)   (.6,.2) ,

AB

( A @ B ) ^T = (^

vA +vB.

ji        ji

)

and

Since A and B are two symmetric intuitionistic fuzzy soft matrices then ^AA and ^AA

^4    ^ Ji             J'

From the above, it is clear that ( A @ B ) ^T = A @ B

Numerical Example

If the above two intuitionistic fuzzy soft matrices are considered, then we see that

AT

(.1,.2)   (.5,.4)   (.5,.2)

(.5,.4)  (.2,.3)   (.3,.4)

(.3,.6)   (.5,.1)   (.6,.2)

' (.3,.3)

A @ B = (.55,.35)

I (.55,.4)

(.55,.35)   (.55,.4)'

(.45,.25)  (.45,.35)

(.45,.35)  (.65,.2)) ,

Then ATA is to be calculated.

Let A^TA= [A ij ], where

A11=[max(.1, .5,.3), min(.2, .4, .6)] =(.5, .2)

A12=[max(.1, .2, .3), min(.4, .4, .6)]

=(.3, .4)

A13=[max(.1, .5, .3), min(.6, .4, .6)]

=(.5, .4)

A21=[max(.1, .2, .3), min(.4, .4, .6)]

=(.3, .4)

A22=[max(.5, .2, .5), min(.4, .3, .1)] =(.5, .1)

A23=[max(.3, .2, .5), min(.6, .2, .2)] =(.5, .2)

A 31 =[max(.1, .5, .3), min(.6, .4, .6)] =(.5, .4)

A 32 =[max(.3, .2, .5), min(.6, .3, .2)] =(.5, .2)

A 33 =[max(.3, .5, .6), min(.6, .1, .2)] =(.6, .1)

Thus

	(.5,.2)	(.3,.4)	(.5,.4)
A T A =	(.3,.4)	(.5,.1)	(.5,.2)
	_ (.5,.4)	(.5,.2)	(.6,.1)

From the above result, it is clear that ATA is also a symmetric intuitionistic fuzzy soft matrix.

Proof of vii

Let A and B as mentioned above are two symmetric intuitionistic soft fuzzy matrices. Then it is to be proved that ATBA is again a symmetric intuitionistic fuzzy soft matrix.

Here let A^TB=[E_i j ], where

E 11 =(.5,  .4), E 12 =(.5,  .3), E 13 =  (.4,  .2), E 21 =(.5,  .2),

E 22 =(.5, .3), E 23 = (.5, .1), E 31 =(.6, .2), E 32 =(.5, .2) and E 33 =(.6, .2).

Hence

A T B =

' (.5,.4)

(.5,.2)

. (.6,.2)

(.5,.3)

(.5,.3)

(.5,.2)

(.4,.2) " (.5,.1) (.6,.2) ,

Again if A^TBA=[G_i j ], then

G 11 =(.5, .4), G 12 =(.5, .2), G 13 = (.5, .2), G 21 =(.5, .2),

G 22 =(.5, .1), G 23 = (.5, .2), G 31 =(.5, .2), G 32 =(.5, .2) and

G 33 =(.6, .2).

Thus

' (.5,.4)

AT BA = (.5,.2)

. (.5,.2)

(.5,.2)  (.5,.2) '

(.5,.1)   (.5,.2)

(.5,.2)  (.6,.2) ,

From the above, it is clear that ATBA is again a symmetric intuitionistic fuzzy soft matrix.

Proof of viii

From above, we have

A и B =

' (.5,.2) (.6,.3)

_v (.8,.2)

(.6,.3)

(.7,.2)

(.5,.1)

(.8,.2) " (.5,.1) (.8,.1) ,

Then it can be obtained that

( A и B )$ C

' (7.15,7,08)  (7.30,7.12)  (748,7.02) '

= (730,712)  (7.42,706) (720,706)

(748,702)  (720,706)  (7.56,7.02),

Thus it is seen that if A, B and C be three symmetric intuitionistic fuzzy soft matrices then ( A и B )$ C is again a symmetric intuitionistic fuzzy soft matix.

Proof of ix

Proceeding as above, it can be shown that if A, B and C be two symmetric intuitionistic fuzzy matrix, then ( A n B )$ C is again a symmetric intuitionistic fuzzy soft matrix.

Proof of x

Let A = ( ^ A ,v A ) , B = ( m b ,V B ) and C = ( m c ,VC ) be three symmetric intuitionistic soft fuzzy matrices. Then

mA+mB vA + v,B

A @ B = (,       )

and

( A @ B )$ C

/ (U "h U 3 LI

= (^( ^{( M} j    M- j ^{) M} j ),

))

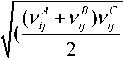
Since A, B and C are symmetric intuitionistic fuzzy soft matrices then

I Ц

( l( O M ij— M ij- M i L 2

)

))

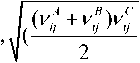
( v a + V B ) v ^c

₍ ji        ji ji

A  BC

( ^M j*    ^M )i >^M j

This shows that ( A @ B )$ C is again a symmetric intuitionistic fuzzy soft matrix.

Numerical Example

We have

( (.3,.3)

A @ B = (.55,.35)

. (.55,.4)

(.55,.35)

(.45,.25)

(.45,.35)

(.55,.4) '

(.45,.35)

(.65,.2)) ,

and then it can be obtained that

(A@B)$C' (7.09,7.12)  (ТЖТ^с)  (^Гзз0,^Гo4) ^

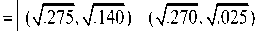
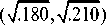
(7Жл/04)  (ТЖ V.210)  (7.455,7.04) ?

This proves the property ( x) .

• [12]    Chetia, B., Das, P. K. , “ On Fuzzy Soft Matrix Theory ” , Journal of Assam Academy of Mathematics , 2010,2, 71-83

• [13]    Verma, R., Dev Sharma, B., “Some new Results on Intuitionistic Fuzzy Sets”, Proceeding of the Jangjeon Mathematical Society, 2013, 16(1), 101-114

• [14]    Rajarajeswari, P., Dhanalakshmi, P., Intuitionistic fuzzy soft matrix theory and its application in decision making, International Journal of Engineering Research & Technology , 2013, 2 (4) .

• [15]    Dhar, M., Study of some properties of intuitionistic fuzzy soft matrix, International Journal of Information Engineering and Electronic Business, 2016, 8(2), 37-45 .

V. Conclusion

Here the main intention was to study the transpose of intuitionistic fuzzy matrices and symmetric intuitionistic fuzzy soft matrices. Some of the properties of transpose of intuitionistic fuzzy soft matrices have been discussed and verified with numerical examples. Further, symmetric intuitionistic soft fuzzy matrices are defined and some properties associated with symmetric intuitionistic fuzzy matrices are discussed with numerical examples. It is seen that some properties of transpose of intuitionistic fuzzy soft matrices and also those of symmetric intuitionistic fuzzy matrices coincides with those of classical matrices and fuzzy matrices. In future, the main concentration will be in the direction of considering all the other properties of classical matrices in terms of intuitionistic fuzzy soft matrices.

Acknowledgement

The author is grateful to all the referees for their valuable suggestions in the preparation of the article.